轨道曲线参数检测算法优化

李颖 程朝阳 陆永彪 陈仕明 余宁 秦哲 那强

1.中国铁道科学研究院集团有限公司 基础设施检测研究所， 北京 100081； 2.北京铁科英迈技术有限公司， 北京 100081

曲线地段轨道在列车离心力的作用下，比直线地段受力大，轨道几何尺寸不易保持，是铁路线路的薄弱环节。轨道曲线参数的平顺性关系到列车运行的平稳性与稳定性，影响列车通过曲线地段容许的最高运行速度。为使曲线保持圆顺，维护良好状态，工务部门根据轨检车提供的周期性检测数据对线路进行调整，因此对轨道曲线参数准确检测提出了要求［1］。

目前国内广泛使用的是GJ-6 型轨道检测系统以及最新研制的数字式轨道检测系统，能够检测的曲线半径为R= 150 ～ 12 000 m，但是对R= 5 000 ～ 8 000 m的曲线线路检测准确性不高，对于提速线路和高速线路上R＞ 8 000 m的大半径曲线线路的识别和检测准确性较低，从而导致系统提供的轨道不平顺超限大值所在的曲线线型（缓和曲线、圆曲线、直线）往往存在误判。同时，对曲线的起始位置、平均半径、长度等参数检测的准确性低、偏差大，使得系统提供的曲线摘要报表和数据利用率较低。

国内在役的轨道检测系统使用步长跟踪曲线线型的方法计算曲线相关参数，但是该方法受跟踪步长和设定阈值参数的影响，对不同大小的半径不能自适应选择参数，检测准确性达不到要求。侯广东［2］提出拟合迭代算法识别曲线关键参数，该方法受迭代终止阈值的影响，线型分段自动化能力有限。熊丽娟等［3］提出使用霍夫变换、稳健估计和迭代法三种基本算法对曲线关键参数先进行识别，再进行拟合与迭代，使用轨道检查仪采集数据进行后处理，实现较为复杂，不适用于车载轨道检测实时系统。

曲线参数检测时，只要确定曲线的直缓点、缓圆点、圆缓点、缓直点四大特征点的准确位置，就能准确计算曲线平均半径、长度、线型等参数。轨道检测系统曲线检测数据具有明显的时间和空间特征，空间上无交叉和重复，与地理测绘领域中运动轨迹数据特征提取类似［4］。轨迹特征提取算法有两种：①线性分段法［5］，算法简单且计算复杂度低；②非线性拟合法［6］，其结果更接近真实轨迹，但算法复杂，计算量大。在线性分段轨迹特征提取的经典算法中，DP 算法［7］最具代表性。该算法是一种线性压缩算法，能有效提取曲线轨迹特征点，运算复杂度较低。其主要思想是将复杂线段进行抽稀和压缩［8］，从而寻找出线型变化处的特征点，但是DP 算法在局部细节上不能很好地反映曲线走向特征。本文根据轨道检测系统曲线检测数据特点，提出在经典DP 算法粗略确定曲线特征点的基础上，在特征点周围窗口内使用角度阈值法提取角点，再将各个角点逐一连线成为走向段，设定阈值寻找极值走向段，根据极值段筛选出曲线线型变化处的全局特征点，实现对曲线相关参数的准确检测。

1 轨检系统曲线检测数据特点

车载轨道检测系统通过安装在车体或检测梁内的惯性和位移传感器来测量曲线相关参数，要求传感器信号带宽不能太高，以免噪声信号叠加到线型数据中，干扰曲线特征点的准确获取。目前在役的轨道检测系统能输出曲率、曲率变化率、曲线正矢等曲线相关检测波形，在利用这些数据之前需要对信号进行预处理，降低噪声信号的影响。在多种信号滤波方法中，选取能有效去除噪声又能保持曲线线型不失真的线性高斯滤波算法对传感器信号进行预处理滤波。高斯滤波窗口长度不宜设置过大，按照轨检系统空间0.25 m 采样间隔，一般选取100 ～ 120 m 窗口长度，以防止曲线特征点被滤除，同时可以满足检测系统延时输出最大长度限制。本文选取窗口长度120 m 进行高斯滤波（图1），可以看出轨道曲线线型变化的特点，整体形状类似于互相间隔的梯形，存在变形并含有噪声，使得底边与斜边的转折点不易准确确定。

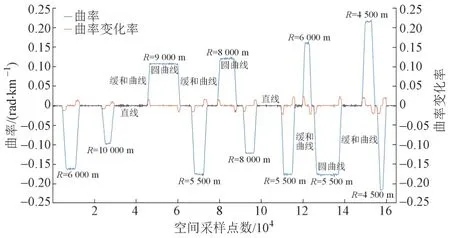
图1 曲线检测数据预处理

2 DP算法提取特征点

车载轨道检测系统虽然是在线实时检测系统，但内部需要根据数学模型作计算和滤波处理，运算需要积累一定长度的区段数据，而且曲线摘要报表的输出是按各铁路局或者工务段管辖区段进行统计，因此可以应用DP 算法对曲线线型数据进行特征点提取。DP算法的基本思路［8］为：设置一定长度（L）区段，连接区段的首尾两点形成一条直线，计算区段内所有点到直线的距离，将最大距离（Dmax）与设定的阈值（D）进行比较，若Dmax＜D则将这一区段上所有中间点都删除；若Dmax＞D则保留此坐标点，并以该点为界，将区段分为两部分，对这两部分递归使用该方法。原理见图2。该算法能够删除曲线上的非特征点，寻找最有代表性的特征点，不足之处是在局部细节上不能很好地反映曲线的走向特征。

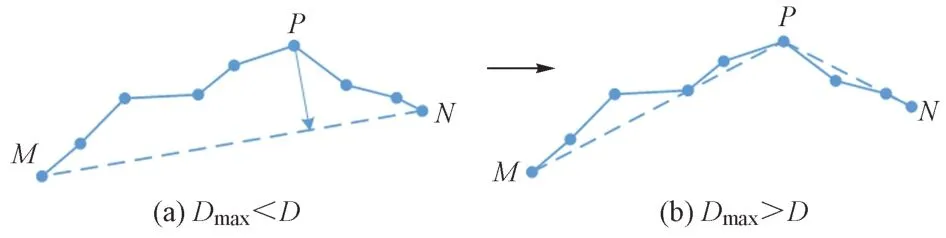
图2 DP算法提取特征点原理

如图3 所示，对一铁路轨道部分曲线数据使用纯DP 算法进行特征点提取。该段线路设计半径5 000 ～12 000 m。首先设定距离阈值（D），使用经典DP 算法得到曲线的粗略特征点和轨迹，D可以稍大，使DP 算法迭代次数减少，提高计算速度。L根据需要统计或检测的里程确定，D根据曲率数值选取。在动态轨道检测系统中曲率的单位为rad/km，对于半径5 000 ～12 000 m 的区段，可以取D= 0.02 km。由图3 可以看出，使用DP 算法能够提取特征点并确定曲线线型变化轨迹，但直缓点、缓圆点、圆缓点、缓直点四个线型变化特征点的位置存在偏差。特征点位置偏差不仅使检测系统提供的曲线起始位置、曲线长度、平均半径、限速半径等曲线参数的检测结果产生较大误差，还会对高低、轨向、轨距、水平、三角坑等轨道几何参数超限峰值所在的线型出现误报，因此须要对算法进行改进。

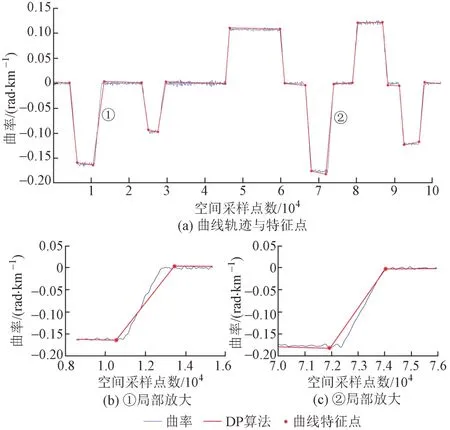
图3 使用DP算法提取曲线轨迹与特征点

3 曲线线型变化特征点提取算法

使用DP 算法能够从全局出发确定轨迹线的特征点，保留曲线数据的整体形态，但是对四大特征点位置的确定不够精准，须要进一步采取局部特征提取方法。因此，在使用DP 算法确定粗略特征点的一定宽度窗口内，依据角度阈值法筛选角点［9］，再将所有角点连线成为走向段，设定阈值寻找极值走向段，从而准确得到曲线线型变化处四大特征点。

3.1 角点提取

角点是计算机视觉领域提出的概念，可应用于轮廓曲线的特征点提取，其定义为曲线上局部曲率最大值点［10］。本文对DP 算法确定的粗略特征点窗口内角点提取方法为：设定角度阈值（φ），依次顺序获取窗口内曲线数据的3 个点，计算相邻两点连线的夹角θi1和θi2；根据式（1），将αi与φ进行比较，若αi≥φ则将该点放入角点集合（S）中。

设定曲线上窗口内数据点之间角度变化值作为选择角点的依据。用绝对角度来度量曲线轨迹变化，规避了丢失曲率变化特征点的问题，同时也避免了使用斜率差提取角点方法带来的非线性弊端。

3.2 曲线线型变化特征点提取

轨道检测系统的曲线检测数据虽然通过多种信号处理，但是仍然存在噪声，而且线路上曲线的圆顺性并不理想，存在大值波动。噪声和大值波动的存在容易使曲线趋势特征被破坏并形成多个特征点［11］。通过角度阈值法筛选的曲线角点集合（S)，可能由局部特征点、转折点、极值点、波动较大的非极值点等组成的，因此要再次对这些角点进行评价和筛选，确定准确的曲线四大特征点。将S中相邻的两个角点逐一连线成为走向段，使寻找表征曲线线型变化特征点的问题转化为寻找极值走向段的问题，采用顺序对比走向段直至确定极值段［12］，该极值段对应的角点即为曲线线型变化四大特征点。

将角点集合S={s1，s2，…，sN}中两个相邻角点连线，以其平均值tj=(sj+sj+1)/2 代表该走向段，表征该段的趋势程度，tj∈T，其中T为走向段集合，T={t1，t2，…，tM}。当轨道曲线线型转变时会存在一个极值段，设定阈值（ξ)对极值段进行筛选。筛选条件为：{tj＜tj-1}∩{tj＜tj+1} 或 {tj＞tj-1}∩{tj＞tj+1}，|tj-tj-1|＞ξ或|tj-tj+1|＞ξ。

当极值段为极大值时，极值段角点大的点为曲线线型变化特征点；当极值段为极小值时，极值段角点小的点为曲线线型变化特征点。

曲线线型变化四大特征点提取算法步骤：①设置DP 算法距离阈值，粗略特征点周围窗口宽度、角度阈值、走向段极值阈值。②轨道曲线检测原始信号数据采用高斯滤波进行预处理。③使用DP 算法确定粗略特征点。由于此步为粗筛，对距离阈值的选取可以稍微增大，以降低DP 算法的迭代次数，提高运算时间。④在已确定的窗口宽度内提取角点。根据式（1）依次计算窗口内曲线相邻数据点的角度变化值，当角度变化大于角度阈值时，把该点加入角点集合。⑤将相邻角点连线为走向段，以角点平均值建立走向段集合。⑥确定极值走向段并确定曲线线型变化全局特征点。根据筛选条件删除走向段集合内不满足条件的区段，得到极值走向段。极值段为极大值或极小值时，取相应极值段角点大或小的点为曲线线型变化最终特征点。

由于DP 算法能够确定曲线特征点的粗略位置，结合TB 10098—2017《铁路线路设计规范》对5 000 m以上大半径曲线线路中缓和曲线的设计要求，窗口宽度取50 m 较为合适；角度阈值的选取根据自适应阈值法，依次计算窗口宽度范围内相邻两点连线夹角的平均值作为角度阈值；走向段极值阈值的选取可以稍大，避免特征点具有局部性，同时减少计算量。

算法流程见图4。

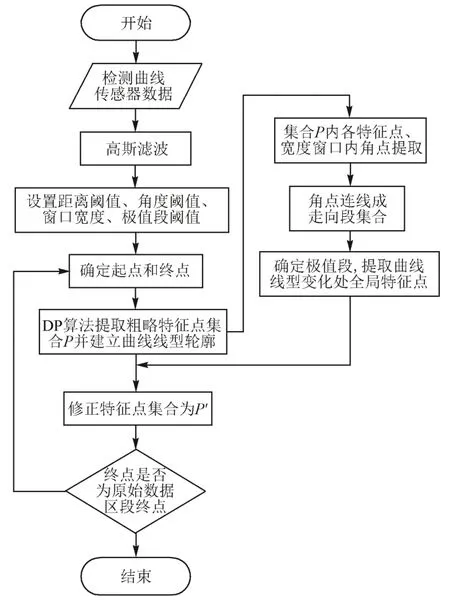
图4 算法流程

4 算法验证

将本文提出的算法应用到车载轨道检测系统曲线参数检测中，与只采用DP 算法提取的特征点进行对比，见图5。可知：纯DP 算法提取的特征点往往受噪声和大值波动的干扰，线型变化特征点位置不够准确；本文算法提取的线型变化特征点在DP 算法的基础上进行了修正，准确性得到提高。

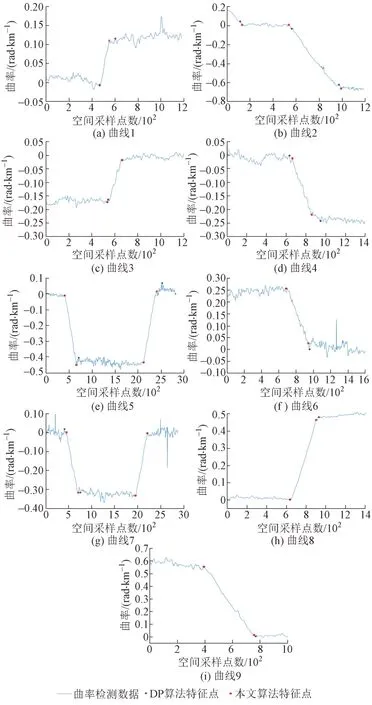
图5 部分曲线数据特征点提取

对于图3 曲线数据，使用本文算法对四大特征点位置进行修正（图6），可以明确看出曲线线型变化处，圆缓点、缓直点位置更加准确。

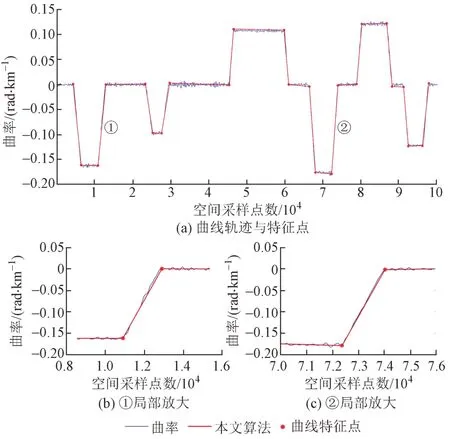
图6 本文算法提取曲线轨迹与特征点

为了进一步验证算法的准确性，使用本文提出的算法与在役轨道检测系统现有算法、纯DP 算法进行对比，对某高速铁路和普速铁路线路的曲线进行检测，部分曲线参数检测数据见表1。其中台账为对应线路上曲线标准设计半径和长度参数。以台账数据为参考标准值，根据表1数据进行准确率统计对比，见表2。本文不考虑检测数据和台账之间的里程偏差。

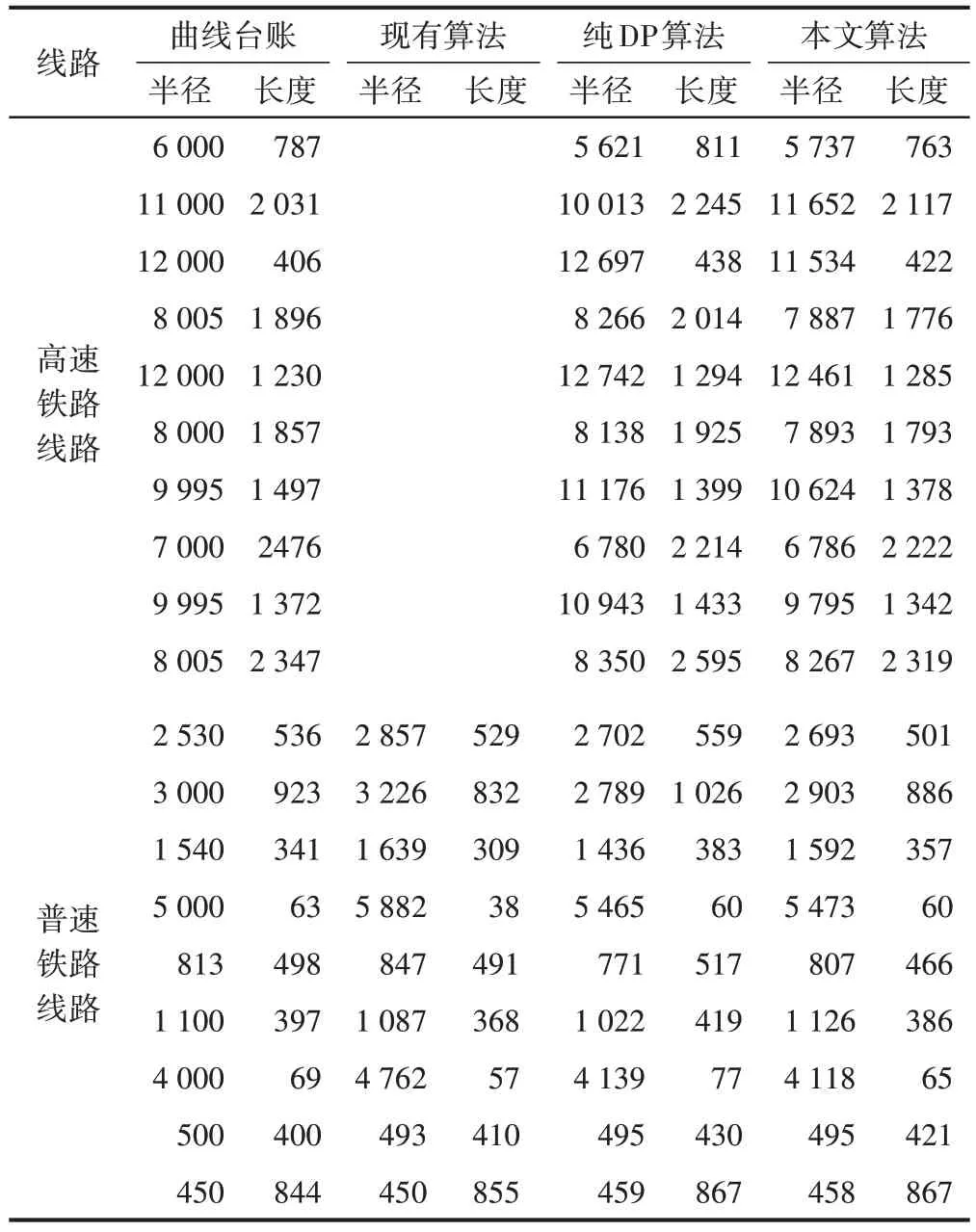
表1 三种算法曲线参数检测结果对比 m

表2 三种算法曲线参数检测准确率对比

由表1 和表2 可知：对半径5 000 ～ 12 000 m 的高速铁路线路大半径曲线，轨道检测系统曲线检测现有算法无法检测出数据，使用纯DP 算法对曲线半径和长度参数检测的平均准确率为93.5%，使用本文算法可达95.8%；对半径5 000 m 以下的普速铁路线路，现有算法对曲线半径和长度检测的平均准确率为91.1%，使用纯DP 算法为93.7%，使用本文算法可达95.8%。经过大量的数据测试和验证，本文算法对曲线参数检测的平均准确率能达到95%以上。

5 结论

本文在轨道检测系统曲线参数检测中引入经典DP算法提取曲线线型变换粗略特征点，在粗略特征点一定窗口宽度内使用角度阈值法提取角点，将角点连线成走向段，通过寻找极值走向段的方法确定曲线线型变化处准确特征点，根据准确的四大特征点位置来计算曲线平均半径、长度等曲线参数。本文算法能够准确确定轨道曲线线型变换四大特征点的位置，对大半径和小半径曲线的检测准确率均达到95%以上，具有良好的适应性，能够更好地为铁路工务部门服务。