基于响应面法的非对称钢桁斜拉桥参数敏感性分析

占玉林 黄媛媛 范梓浩 邵俊虎 覃早

1.西南交通大学 土木工程学院， 成都 610031； 2.西南交通大学 土木工程材料研究所， 成都 610031；3.成都大学 建筑与土木工程学院， 成都 610106； 4.中铁二局第五工程有限公司， 成都 610091

钢桁梁斜拉桥具有造型美观、跨越能力强、承载能力大等优点，在大跨度铁路及公铁两用桥梁应用较广泛。桁架结构的主梁形式使得结构的竖向刚度更易于控制，也更加易于满足桥梁在抗风特性方面的要求；钢材作为一种各向同性均匀介质，具有很好的强度和韧性，同时便于钢梁节段在工厂完成预制，提高了桥梁施工的精度［1］。大跨度非对称钢桁斜拉桥与普通斜拉桥同属于高次超静定结构，成桥后结构的线形及内力受到多种参数的影响［2］，如温度［3］、拉索索力、主梁重量、结构构件的制造误差等，使得成桥状态与理想设计状态之间存在偏差。高低塔斜拉桥由于结构的非对称性，在施工阶段及成桥状态下的受力、变形特点又不同于普通的对称式双塔斜拉桥。

针对等塔高双塔斜拉桥参数敏感性分析已有较多研究，而针对非对称高低塔钢桁斜拉桥系统的参数敏感性分析还较少。

国内学者一般采用单一参数调整法进行敏感性分析［4-9］。它是在有限元模型中分别给定单一参数的变化幅度，其他参数保持不变，计算出结构响应的变化大小，然后根据影响程度确定敏感参数和不敏感参数。但这种方法仅分析了一定变化幅度下参数对结构响应的影响，需要多次修改有限元模型进行分析计算，具有较大的局限性［10］。与该方式不同，张治成［11］采用梯度分析方法对南浦大桥进行敏感性分析，引入了影响百分比的概念，使各参数对施工控制目标的影响程度有了更直观的表示。梯度分析法通过研究目标函数Ψ（X，Y）在最优点（X，Y）处对设计参数X的梯度值来进行结构敏感性分析。这种方法可以假定控制目标函数为Z = Ψ（X，Y），分析某设计参数XK对控制目标的影响敏感性时，令XK在其基准值一定范围内变动，而其余参数取基准值不变，对目标函数求偏导，从而得到各个设计参数的梯度值［10］。但与单一参数调整法一样，该方法仍需要进行多次有限元计算，有一定局限性。

以上两种方法在进行参数敏感性分析时都需要多次代入有限元计算且不能将设计参数与结构响应之间的关系显式化，而响应面法正好能补充这两种方法的不足。响应面法已经被广泛应用于解决各种工程问题，如优化设计、可靠性分析、动力学研究、施工过程控制等方面［12］。段力等［13］采用响应面法对重庆鹅公岩轨道专用桥施工临时结构钢箱斜拉桥主梁线形进行影响参数的识别。刘剑等［14］采用响应面法对钢箱斜拉桥静力参数进行了敏感性分析。王达等［15］采用响应面法研究主梁重度、索力及配重3 个设计参数对大跨斜拉桥主梁线形的影响，并通过调整参数来修正主梁线形。许世展等［16］采用响应面法对无背索斜拉桥施工阶段模型计算结果与实际结构响应之间出现的偏差进行动态修正，使最终的成桥状态达到设计状态。

本文采用响应面法构建结构响应与各个影响参数之间的显式关系式，利用梯度算法求解各个参数对某一响应量的敏感度和敏感百分比，探究各个参数对结构响应的敏感程度，研究成果可为大跨径桥梁的参数识别、施工控制等提供参考。

1 基于响应面法的参数敏感性分析原理

1.1 响应面法基本原理

响应面法（Response Surface Methodology，RSM）的基本思想是通过近似构造一个具有明确表达形式的多项式来表达隐式功能函数［11］。响应面法构建结构响应与设计参数之间的关系，可以直接利用现已广泛应用的有限元分析程序，通过拟合的二次曲面来近似模拟真实结构响应曲面，具有较高的效率，能很好地满足实际工程的精度要求［17-18］。

本文采用包含二次项的多项式来构造响应面方程，见式（1）。式中由于不包含各设计变量的二次交叉项，在设计参数数量相同的情况下，待定因子较少，因而构造结构响应方程所需的样本数更少，特别是当设计变量数量多的情况下，求解时间大大缩短，效率更高。

为验证模型的准确性和预测能力，通过回归分析来判断二次响应面模型的拟合程度，本文采用决定系数（R2）和均方根误差（Root Mean Square Error，RMSE）来对模型进行检验，见式（2）和式（3）。其中，R2表示响应面与真值之间的差异程度，在0～1取值，其值越大则回归模型越接近实际情况；XRMSE表示响应面的精度，其值越小，表示响应面模型的精度越高。

1.2 敏感度及敏感百分比

在求得响应面方程后，通过敏感度表述目标函数对设计变量Xi的变化梯度。若可导，在连续系统中各参数的一阶敏感度（SXi）和设计变量敏感百分比（γXi）的表达式分别为

针对非对称钢桁斜拉桥敏感性分析，首先确定了研究参数和结构响应［19］，其次根据选取的研究参数样本代入有限元模型中获得各个响应计算值，然后根据响应面法基本原理拟合响应面方程，最后再利用梯度算法计算各个参数对结构响应的敏感度和敏感百分比，具体流程图见图1。

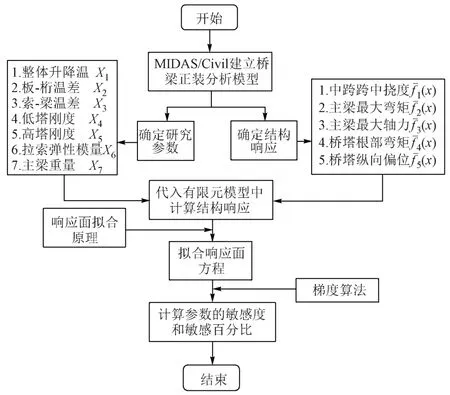
图1 敏感性分析流程

2 工程实例

2.1 工程概况

大跨度钢桁斜拉桥立面见图2。孔径布置为（62.5 + 125 + 425 + 175 + 75） m，桥梁全长877.8 m。桥型为双层四线钢桁斜拉桥，主桁高14 m，宽17 m。索塔采用钻石形索塔，2#索塔高189.5 m，3#索塔高203.0 m，南北边跨分别设置一个辅助墩。上层为预留客运专线，下层为重庆东环线双线铁路。

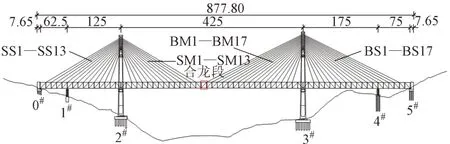
图2 桥梁立面（单位：m）

2.2 有限元模型

利用MIDAS/Civil 建立非对称钢桁斜拉桥全桥模型，模型中共包含8 891 个节点和17 471 个单元。索塔及主梁桁架均采用梁单元模拟，斜拉索采用仅受拉的索单元模拟，桥面系采用板单元模拟。

3 响应面模型的建立

为研究各设计参数对结构响应的敏感程度，模型中考虑了整体升降温、板-桁温差、索-梁温差、低塔刚度、高塔刚度、拉索弹性模量以及主梁重量这7个影响参数。其中，板-桁温差可以看作是一个相对刚度的问题，主桁架纵向刚度大而桥面板纵向刚度小，两者的刚度不同导致内力分配存在较大差异，而两者连接部位不能有效地传递温差效应会对结构内力和变形产生影响［20］。根据当地气象资料，整体升降温设置为15、20、25 ℃，在模型中采用系统温度模拟。板-桁温差设置为5、10、15 ℃，分别考虑钢桁梁升温10 ℃，上层桥面板升温15、20、25 ℃，下层桥面板升温13、16、19 ℃［20］；索-梁温差设置为15、20、25 ℃，考虑钢桁主梁升温10 ℃，拉索升温25、30、35 ℃；高低塔刚度设置为EI、5EI、10EI［21］（E为弹性模量；I为截面惯性矩），通过修改截面刚度特性实现；拉索弹性模量设置为0.95E、1.00E、1.05E［22］，通过修改有限元模型中拉索的材料属性实现；主梁重量设置为0.95W、1.00W、1.05W［22］（W为主梁重量），通过在有限元截面特性调整系数中修改主梁截面重量系数实现。数据样本见表1。表中序号代表不同的参数样本组代表图1 中表示的结构响应；X1—X7代表图1 中研究参数。

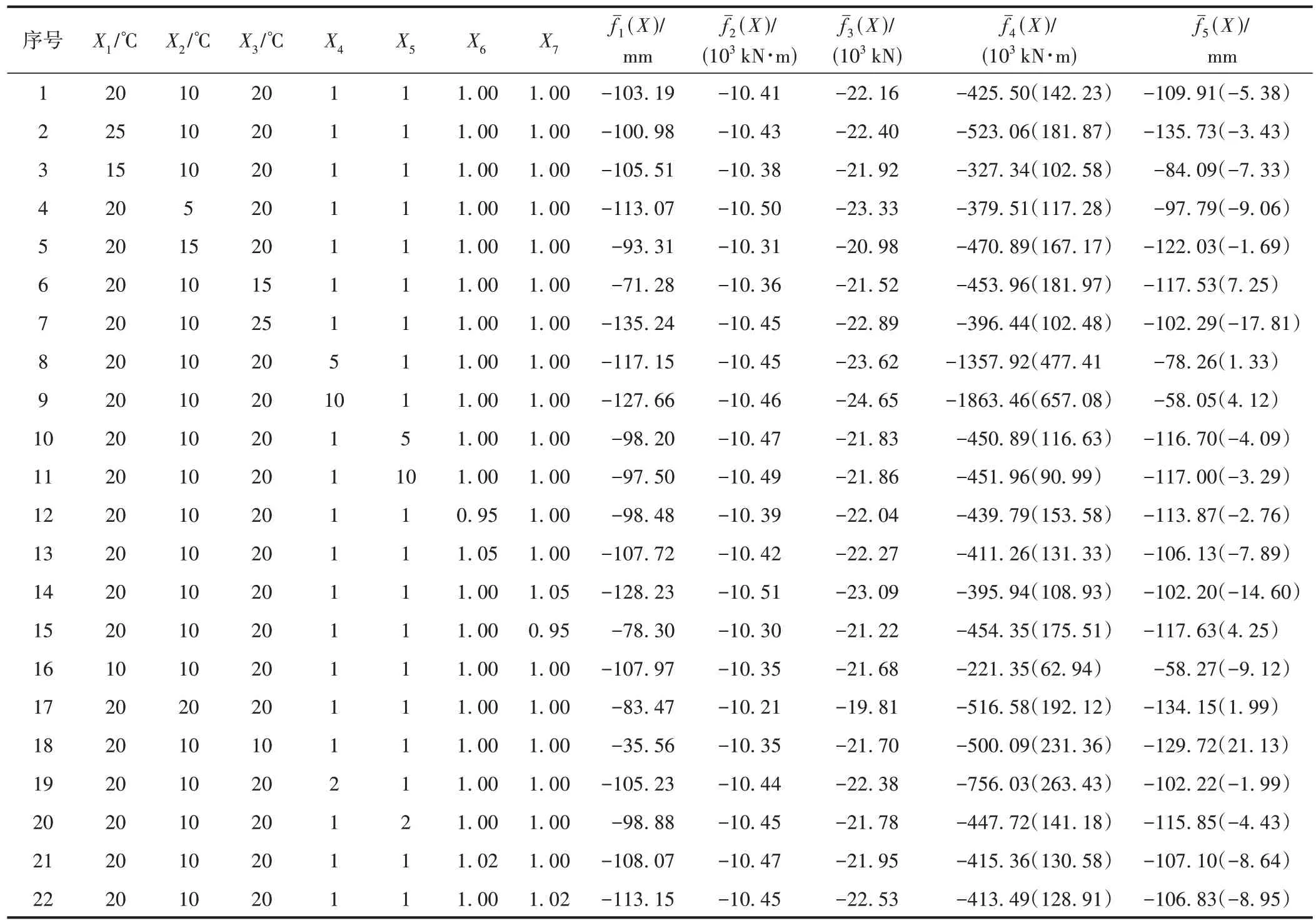
表1 数值模拟试验样本

根据响应面法的基本原理，构建出响应面方程有15 个未知系数k0～k14，见式（6）。因此，需要建立15 个独立方程进行求解，表1 中序号1—15 的数据样本用于构造响应面方程。求解响应面议程系数，见表2。

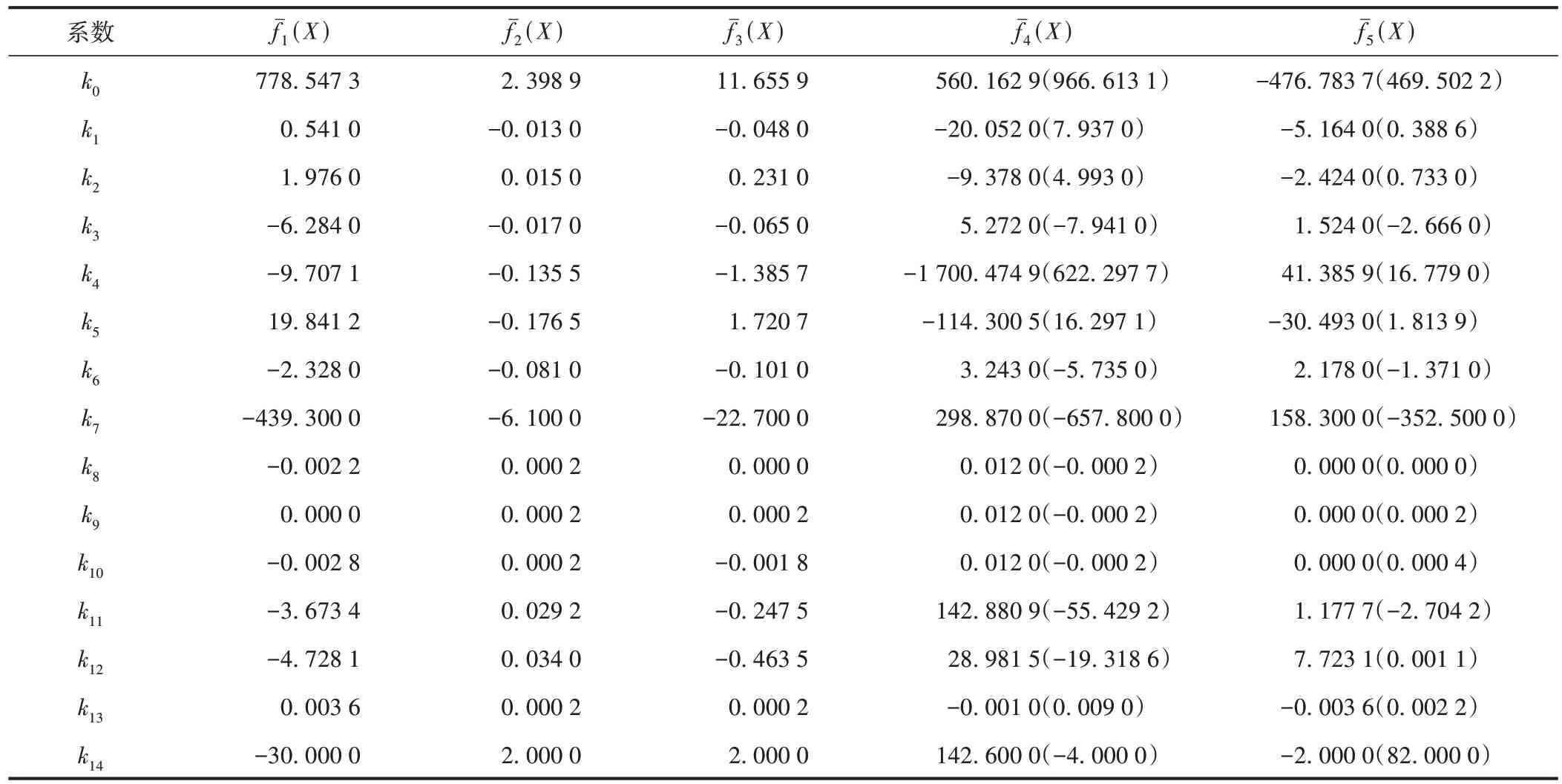
表2 响应面方程系数

为验证响应面方程的准确性和预测能力，将响应面模型的拟合值，即表1 中序号16—22 的数据样本与有限元模型的计算值进行对比，以此来验证方程拟合的吻合程度。

根据式（2）和式（3）计算R2和XRMSE，结果见表3。可知，R2接近1，XRMSE在0.5 以下。说明拟合的两个响应面方程可以很好地反映结构响应和参数之间的关系，可用于结构敏感性分析。

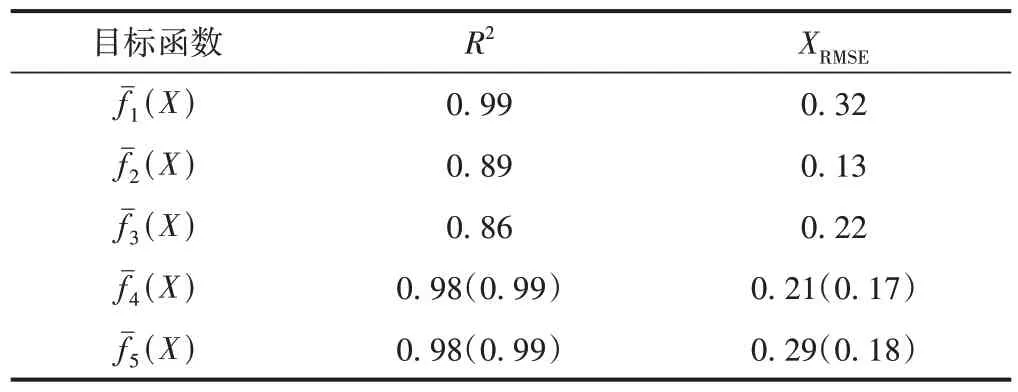
表3 响应面模型评估结果

4 参数敏感性分析

4.1 主梁中跨跨中挠度

主梁线形控制是大跨度斜拉桥在施工和运营阶段都十分重要的一个结构响应，对其进行敏感性分析可以了解各个参数的影响程度，并对主要影响参数加以控制。本文仅对主梁中跨跨中挠度进行参数敏感性分析。各参数的敏感度及敏感百分比计算结果见图3。

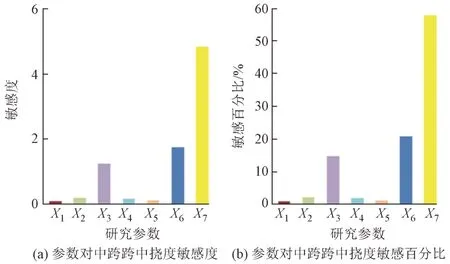
图3 中跨跨中挠度敏感性分析结果

由图3 可知：主梁重量对中跨跨中挠度的影响最明显，敏感度为4.86，即主梁重量每增加1%，中跨跨中挠度要增大4.86%，且敏感百分比高达57.81%；索-梁温差和拉索弹性模量的影响程度次之，敏感度分别为1.24和1.75，敏感百分比为14.81%和20.86%；其余4 个参数的敏感度均小于1，敏感百分比分别为2.29%、1.97%、1.20%和1.05%。

4.2 主梁最大弯矩

主梁的内力反映了主梁的受力情况，若超过规范限值将严重危害桥梁安全。因此，将主梁最大弯矩作为研究对象，对各参数进行敏感性分析，计算结果见图4。可知：主梁重量对主梁最大弯矩的影响最明显，敏感度为0.20，且敏感百分比高达62.86%；拉索弹性模量的影响程度次之，敏感度为0.05，敏感百分比为17.51%；其余5 个参数的敏感度均小于0.02，敏感百分比分别为5.69%、5.39%、3.25%、2.31% 和2.99%。

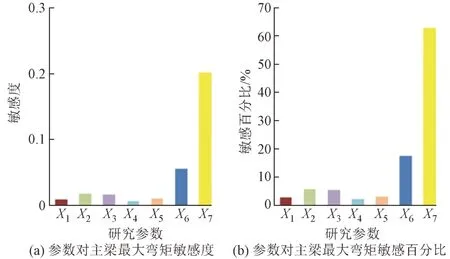
图4 主梁最大弯矩敏感性分析结果

4.3 主梁最大轴力

对于钢桁斜拉桥而言，主梁内力除了弯矩外，还应考虑轴力。轴力对主梁的应力水平起到了关键作用。因此，提取主梁最大轴力作为研究对象，对各参数进行敏感性分析。计算结果见图5。

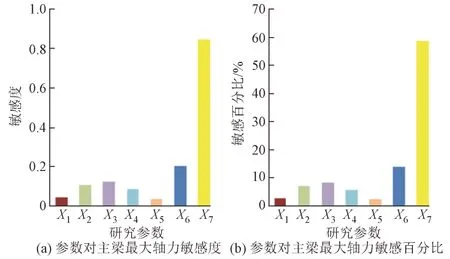
图5 主梁最大轴力敏感性分析结果

由图5 可知：主梁重量对主梁最大轴力的影响最为明显，敏感度为0.84，敏感百分比为58.60%；拉索弹性模量、索-梁温差和板-桁温差的影响程度次之，敏感度分别为0.20、0.12、0.10，敏感百分比分别为14.06%、8.59%、7.36%；其余3 个参数的敏感度均小于0.01，敏感百分比分别为5.89%、3.01%和2.49%。

4.4 桥塔根部弯矩

桥塔根部弯矩是桥塔最不利的受力部位。非对称式斜拉桥的两个主塔高度不同，分别提取了高塔和低塔根部截面的弯矩，对各设计参数进行敏感性分析，计算结果见图6和图7。

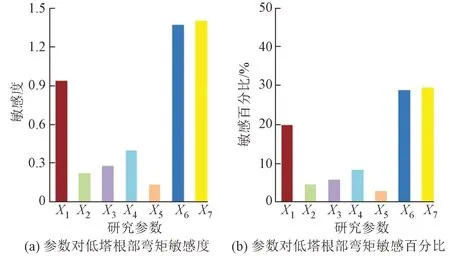
图6 低塔根部弯矩敏感性分析结果

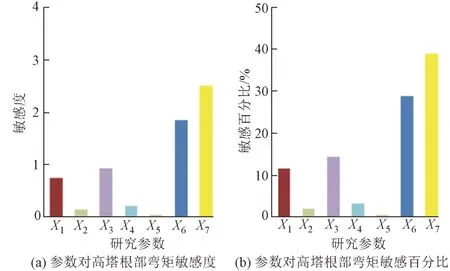
图7 高塔根部弯矩敏感性分析结果

由图6 和图7 可知：无论是低塔还是高塔根部弯矩，主梁重量和拉索弹性模量对根部弯矩的影响较明显，低塔的敏感度分别为1.40 和1.37，高塔的敏感度为2.50和1.86。对于低塔根部弯矩，整体升降温影响次之，敏感度和敏感百分比分别为0.95、19.78%；其余4 个参数敏感度均在0.4 以下。对于高塔根部弯矩，索-梁温差和整体升降温的影响程度次之；其余3个参数敏感度均在0.4以下。

4.5 塔顶纵向偏位

索塔塔顶在不平衡水平力作用下会产生偏位，若偏位太大将会严重影响索塔受力，甚至对全桥受力和变形产生危害。因此，提取低塔和高塔纵向偏位作为研究对象，对各参数进行敏感性分析，计算结果见图8和图9。

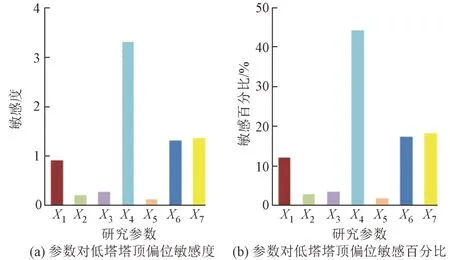
图8 低塔塔顶偏位敏感性分析结果

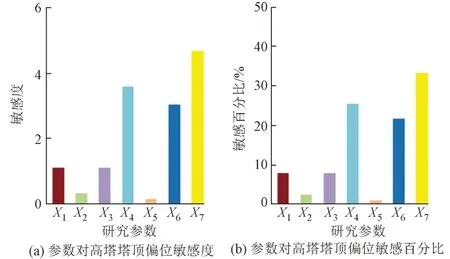
图9 高塔塔顶偏位敏感性分析结果

由图8 可知：低塔刚度对低塔塔顶纵向偏位的影响最明显，敏感度和敏感百分比分别为3.32、44.08%；主梁重量、拉索弹性模量和整体升降温的影响程度次之，敏感百分比分别为18.20%、17.33%和12.19%；其余3个参数的影响程度较小，敏感百分比小于4%。

由图9 可知，主梁重量对高塔塔顶纵向偏位的影响最明显，敏感度和敏感百分比分别为4.68、33.27%；低塔刚度和拉索弹性模量对高塔塔顶偏位的影响程度次之，敏感百分比分别为25.56%和21.68%；其余参数影响程度小，敏感百分比均低于10%。此外，塔顶纵向偏位对低塔刚度的敏感程度远大于高塔刚度，增大低塔刚度能有效减小塔顶纵向偏位。

5 结论

本文根据工程实例，考虑了7 个主要的设计参数和5个重要的结构响应来构建响应面方程进行敏感性分析，研究结果可为非对称钢桁斜拉桥敏感性分析提供参考，也可应用于桥梁施工控制和参数识别，确定主要影响参数。主要结论如下：

1）响应面法可建立结构响应与设计参数之间的显式表示式，大大提高了结构分析效率。基于响应面法的参数敏感性分析方法概念清晰、计算合理，可用于区分不同参数对结构响应的影响程度。

2）通过对响应面方程的拟合及各参数的敏感性分析，可以看出主梁重量对结构各个响应的影响程度始终处于最高或者次高位，而其余设计参数对不同的结构响应均表现出不同的影响程度。同一设计参数对不同结构响应的影响程度可能不一致。