一种室内伪卫星混合指纹定位方法
李雅宁,李宏生,蔚保国
(1.东南大学 仪器科学与工程学院微惯性仪表与先进导航技术教育部重点实验室,江苏 南京 210096;2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;3.卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081)
1 引 言
与室外开放自由空间相比,室内信道环境和空间拓扑更为复杂,由于建筑物遮挡的衰减,卫星导航系统(Global Navigation Satellite System,GNSS)信号服务无法在室内环境中有效覆盖。伪卫星是一种地面导航发射机,可以传输与卫星导航系统兼容的信号。在室内环境中,伪卫星通过发射天线向用户终端发射类似于空间卫星信号的信号,可以通过软件升级提供室内和室外连续定位服务,而无需改变市场上现有的智能终端硬件[1]。
但在室内环境中,伪卫星信号在多径传播和阴影遮蔽的影响下会产生路径损耗和多径衰落等传播效应。传统卫星导航系统定位的成熟理论方法并不完全适用于室内伪卫星定位,从而指纹定位被广泛研究。文献[2]提出了一种室内指纹定位传感器融合框架,该框架结合了Wi-Fi接收信号强度(Received Signal Strength,RSS)、智能手机传感器和行人航位推算(Pedestrian Dead Reckoning,PDR)算法,得到了合理的定位精度和更小的惯性传感器误差。文献[3]使用改进的K最邻近(K-Nearest Neighbor,KNN)算法来研究无线指纹定位的准确性,并将其性能与其他指纹定位算法进行比较。文献[4]提出了一种结合指纹定位和动态预测的室内定位算法,能够缓解接收信号强度波动的影响,具有较好的定位精度和稳定性。为降低数据库存储成本与提高指纹质量,研究者们也做了大量相关研究。文献[5]提出了基于静态众包指纹和自适应路径损耗模型插值的指纹库构建方法,能够快速实现指纹库构建,且定位精度与完全人工指纹库基本一致;文献[6]提出了一种基于模糊聚类的精简接入点匹配定位算法,定位精度提高了15%以上;文献[7]提出一种动态校正的信号双尺度近邻定位算法,校正信号波动值以降低定位误差及计算复杂度。
目前基于室内指纹定位的数据形式除了上述接收信号强度之外,还包括信道状态信息(Channel State Information,CSI)。接收信号强度表示叠加在接收点的信号强度值,当它作为惟一的指纹特征时,会忽略如相位等很多有用的信息,从而不能很好地反映信号在信道中的传播特性,只能在一些简单的环境中达到理想的效果。信道状态信息包含幅度和相位信息,可以提供比单值接收信号强度更丰富的频域信息,故在传统的室内环境中比接收信号强度更稳定。文献[8]提出了一种基于载波相位差的室内指纹定位方法,利用伪卫星基站发射的兼容卫星导航系统的卫星信号,与接收信号强度指纹相比,定位精度大大提高。文献[9]提出了一种结合接收信号强度和信道状态信息的定位算法,该算法选择基于深度学习算法的高相关接收信号强度和信道状态信息特征构建指纹库,提高了定位精度。
获取信道状态信息的方法有两种,即基于实际通道测量数据的统计方法和基于电磁数据精确计算的数学方法。前者基于实际测量数据,对不同环境特征的适应性较差,而后者依赖于对环境的理想简化和假设,与实际情况存在不可弥补的偏差。一般来说,确定性方法比统计方法更准确,因为确定性方法不受单次采集错误的影响,但需要详细的先验环境信息,因此计算复杂度高。文献[10-11]验证了仿真指纹的有效性,与实测指纹变化情况基本一致,但对于仿真指纹的研究主要聚焦于与实测指纹的对比分析,并且往往是单一接收信号强度特征。
基于指纹的室内定位技术旨在通过已知的信道状态信息寻找特征值与位置的函数关系,通过匹配技术在线预测室内位置。从广义上讲,只要存在预测、分类或控制问题,就可以引入人工神经网络(Artificial Neural Network,ANN)[12]。目前,研究人员通常侧重于网络架构的改进和各种机器学习方法的横向比较[13-15],而关于神经网络输入的多样性和多维性的研究相对较少。
综上所述,基于神经网络的指纹定位方法能够更准确地描述室内环境特征,实现实时定位。然而,大多数用于训练的数据集是实际采集数据,主要存在以下两个局限性:①未知环境的定位问题。使用基于受控实验环境的实际采集指纹的定位技术,在未采集区域将无法提供定位服务。②为实现室内环境全覆盖,需要多个无线接入点作为信标,定位精度与测试点密度有关。大型室内场馆的高精度定位服务意味着巨大的测试工作量,并且受单次采集误差的影响很大。
文中提出了一种结合实测数据、确定性计算数据和人工神经网络的室内伪卫星模拟信道状态信息指纹定位方法。通过确定性计算方法得到的信道特征参数与实际测量数据一起作为神经网络的训练集。扩展后的输入集提高了在实际采集到指纹区域的定位精度,也可以在实际未采集到指纹的区域完成初步定位。
2 基于射线追踪及神经网络的指纹定位方法
2.1 射线追踪法主要参数
射线追踪(Ray Tracing,RT)是一种将研究环境中的高频电磁波模拟成光波的方法,结合一致衍射理论,被广泛用于研究高频电磁波的传播。在信号频率属于高频段的前提下,信号可以看成是一条在空间和界面上沿直线传播的射线。伪卫星信号采用L频段,属于超高频段,符合光线追迹的理论前提。射线追踪是一种使用麦克斯韦方程组的确定性计算方法,所有电磁射线都根据成像理论追溯到发射源,计算效率高度依赖于环境的复杂性。当射线在物体表面反射时,产生的信号射线的方向由表面材料的反射和折射特性决定,能量由菲涅耳方程计算。类似地,当射线穿透物体(透射)或在物体边缘发生衍射和散射时,菲涅耳方程与成像理论相结合,以确定所得射线的能量和方向。
(1) 接收功率
接收点R处的总接收功率[16]为
(1)
其中,N是路径数,Pi是第i条路径的时间平均功率。Pi可表示为
(2)
其中,λ是波长,η0是自由空间的阻抗(377 Ω),Eθ,i和Eφ,i是接收点第i条路径的θ和φ电场分量,θi和φi表示第i条路径的到达方向。
信号到达接收点的方向由下式给出:
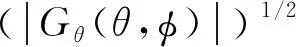
(3)
其中,Gθ是接收天线增益的θ分量,φθ是远区电场θ分量的相对相位。β为发射信号ST(f)的频带与接收机SR(f)可以接收的频带的重叠部分:
(4)
其中,fT和BT分别是发射波形的中心频率和带宽。假设窄带波形是平坦分布的:
(5)
其中,f0是中心频率,B是带宽。
总接收功率为
(6)
(2) 到达时间(Time of Arrival,ToA)
每条传播路径的到达时间为
(7)
其中,Li是第i条电磁射线路径的总长度,c是光速。
2.2 指纹特征的选取
伪卫星接收机输出的原始观测信息包括每个历元的伪距、载波相位、积分多普勒、载噪比等观测值。每种观测量的位置特异性和稳定性都不同,需要进行分析和选择。
(1) 伪距观测量
伪距观测量是卫星导航系统定位中最基本的观测量,是绝对单点定位的必要条件。在复杂的室内环境中,它可以直接反映伪卫星发射天线和接收天线之间的距离,但由于多径传播的影响,伪距测量值精度低、稳定性差。
(2) 载波相位差观测量
载波相位观测量是接收机输出的另一个基本观测量。它表示接收机再现的载波信号的相位与接收机接收到的载波信号的相位之差。载波相位差比伪距差更稳定,基本上是一个恒定值,即伪卫星天线与接收天线的距离差。载波相位差可以消除接收机时钟差的影响,但不能消除特定空间多径的影响,因此可以将其作为信息源添加到特征库中。
(3) 载噪比观测量
载噪比(C/N0)观测值是接收到的载波信号强度与本地噪声之间的比率,描述了接收机接收到的信号的质量。
由于文中不涉及动态测量,因此不关注多普勒观测量。考虑到测量的方便性和数据的稳定性,本研究采用模拟信道参数到达时间和接收信号强度,对应于实测信道状态信息数据中的载波相位和载噪比作为特征值进行位置预测。
2.3 射线追踪-人工神经网络混合指纹定位方法
现有公开文献中用于训练指纹定位的输入层数据来自于在环境中测得的信道状态信息。这种做法导致了许多固有的错误和不便:① 室内环境中存在许多障碍物,墙壁、地板、门窗的材质和厚度对室内伪卫星信号的传播影响很大,环境表征过程比较复杂;② 模型训练存在仅依靠实测数据无法消除的固有误差,如测试人员的个人因素、接收机本身的误差、环境动态变化的误差等;③ 仅依靠实际测量建立指纹数据库时,定位覆盖范围和定位精度受限于采集工作量。
针对人工神经网络用于指纹定位的可行性和实测指纹输入数据的不足,文中设计了一种人工神经网络与射线追踪的混合算法,利用确定性建模产生的特征参数对原有人工神经网络输入进行改进,即室内场景的接收点位置由该区域的低密度测量数据集和高密度模拟数据集联合训练和预测。
实测数据中的载噪比对应于仿真参数中的接收功率。接收点的接收功率首先通过射线追踪确定性模拟得到,然后转换为载噪比,转换过程如下。
接收点的信噪比表示为
(8)
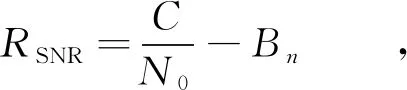
(9)
其中,Bn是接收机的滤波器带宽,S是接收信号功率,N0是噪声功率谱密度,C是载波信号功率。
载噪比与接收功率的换算关系如下:
(10)
对于载波相位定位,卫星P和接收机R之间的距离可以描述为
ρ=λ(φS-φP) ,
(11)
其中,ρ=cti,c是光速,λ是载波波长,φ是载波相位。考虑到时钟差的影响,使用载波相位差更准确:
Δρ=λΔ(φS-φP)=cΔti。
(12)
所提算法框架和流程如图1所示。

图1 混合算法框架
针对室内环境表征过程更为复杂的问题,增加了训练数据集的确定性仿真特征。确定性建模过程综合考虑了建筑物的布局、材质等信息,能更准确地描述环境特点,正向建模过程同时可以消除测试人员的个人因素、接收机本身误差、环境动态变化误差等随机因素;另一个影响指纹定位准确性的因素是特征的变化性,故有必要收集更多的参考点指纹来实现准确定位,特别是当环境变大的时候,所建立的指纹数据库往往是巨大的。浅层学习架构限制了拟合能力,特征提取过程易受信号波动影响,对此考虑增加网络结构中的隐藏层数量,对输入特征多层次的抽象,更好地线性划分不同类型的数据,尤其是不同层之间的全连接多层感知器(MultiLayer Perceptron,MLP)可以获得更鲁棒的训练模型。
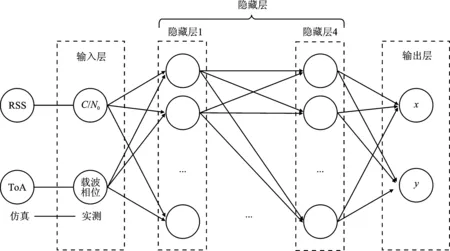
图2 神经网络结构
基于网络收敛速度和准确性的综合考虑,采用的神经网络架构如图2所示,并对此设计仿真和实测实验,通过与传统方法对比分析来验证正确性是否有所提升。输入层包含两个输入特征向量,实际测试数据为载噪比和载波相位这两个与定位结算密切相关的参数,对应确定性建模仿真数据为接收信号强度和到达时间。神经网络有4个隐藏层,第1隐藏层包含30个隐藏神经元,第2层包含20个隐藏神经元,第3层包含10个隐藏神经元,第4层包含8个隐藏神经元。输出层包含两个神经元,为定位位置的坐标(x,y)。一旦满足预测精度或测试集的误差度量在一定数量的连续迭代内没有减少,训练过程就会终止。模型训练及位置预测过程如算法1和算法2所示。该结构在处理大量信道状态信息样本时具有优势,在模型训练中,笔者将重构损失、KL(Kullback-Leibler)散度损失和分类损失一起进行优化。
算法1模型训练。
输入:伪卫星观测量数据集A={a(1),a(2),…,a(n)},射线追踪仿真数据集B={b(1),b(2),…,b(n)},n是伪卫星的数量
位置标签:p
输出:隐含变量特征z与模型参数φ和θ;位置估计模型Mclassifier{(z,p)}
① 初始化:各层隐含单元数量;迭代次数(epochs);隐含空间维数
② while {φ,θ}未收敛
③D←getMinibath()
④μθ,θθ←A+B,p
⑤ 采样ε
⑥ 使用下式后验采样z←qφ(z|(A+B),p)
参数重新赋值:z=μθ+σθε
⑦ 计算变分下界梯度L(重建损失、分类损失、KL散度损失)
⑧ 使得L最小
⑨ end while
⑩ while定位模型训练do
算法2位置预测。
输入:实时观测数据a,定位模型Mclassifier{(z,p)}
输出:预测位置p
① for 每一组ado
② 通过定位模型预测位置:p←Mclassifier{(z,p)}
③ end for
具体实施步骤描述如下:
(1) 在实际环境中进行信道状态信息指纹采集,得到相对稀疏测试点的载波相位差和载噪比的测量值。
(2) 首先根据实际环境的三维地图或材料信息对环境进行建模,然后通过射线追踪计算出相对密集测试点的信号到达功率和到达延迟等模拟信道状态信息。测试点的密度可以根据需要的精度灵活设置。
(3) 模拟数据经式(8)到式(12)转换后,与实测数据一起作为神经网络的输入。
(4) 算法1用于离线模型训练,算法2用于在线位置预测。
人工神经网络的本质是通过根据输入和期望输出调整和修改内部连接的权重来学习。在学习过程中,以最小化损失函数为目标,网络可以通过选择权重和偏差来调整输入参数。与以往不同的是,该网络的训练数据不仅是测量数据,还包括射线追踪计算得到的模拟数据,这扩展了数据集的样本特征。
3 实验验证
3.1 环境建模
实测模拟实验区为某机场到达厅。场景仿真参数如表1所示。6个伪卫星以等分的圆形排列在屋顶上。大厅中轴线有6根承重柱,横截面为边长0.5 m的正方形,墙体承重柱的材料为混凝土,地面材料为瓷砖,伪卫星收发天线为全向天线,环境建模图如图3所示。测试区域1是已采集指纹的区域,该区域先进行人工信道状态信息指纹采集,然后进行确定性建模和仿真,扩展指纹数据集,仿真采样点400个,间隔 0.25 m;测试区域2为未采集指纹区域,仅使用模拟指纹数据进行位置训练和预测,有100个仿真采样点,间隔为0.5 m。实验环境和方法如图4所示。

表1 确定性仿真参数设定
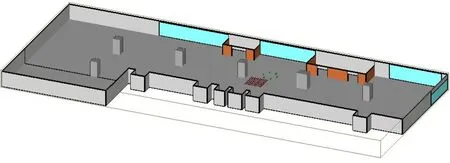
图3 实验环境模型图
3.2 指纹采集
选取25个间隔1 m的位置参考点(人工采样点与位置参考点不重合),测试定位精度。为了直观地显示定位误差,建立了适当的相对坐标系,使25个参考点的横纵坐标为1~5的整数,每个节点的采集时间为 30 s,采集到的数据经过平均和归一化处理后作为神经网络实测部分的输入。
在模拟计算过程中,发射点和接收点之间存在多条传播路径。直达路径传输距离最短,到达功率最强。随着传播距离的增大以及反射透射次数的增加,信号传输距离和相应的传输时延也随之增加,伪卫星信号功率衰减更加严重,直至低于接收信号功率阈值。通过三维射线追踪计算得到图4中区域1的400个测试点和区域2的100个测试点的电磁信息,经过转换和归一化作为仿真输入部分。
3.3 指纹采集区域定位结果
图5为无模拟指纹数据的神经网络定位测试结果,均方根定位误差约为1.069 6 m,平均绝对误差约为 0.333 3 m。图6显示了使用模拟指纹数据进行神经网络定位的测试结果,均方根定位误差约为0.485 0 m,平均绝对误差约为0.145 5 m。通过对结果进行定性和定量比较可以看出,加入确定性模拟输入特征的改进人工神经网络降低了定位测试误差(缩短了真实位置与定位结果的距离),均方根误差减少约54.7%。
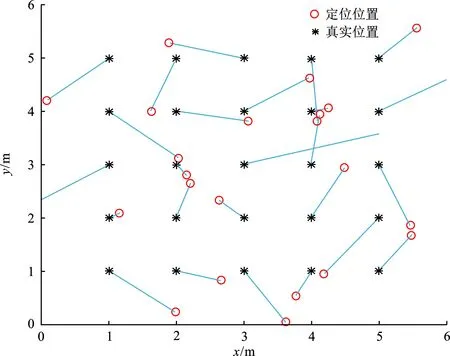
(a) 定位位置与真实位置直线距离
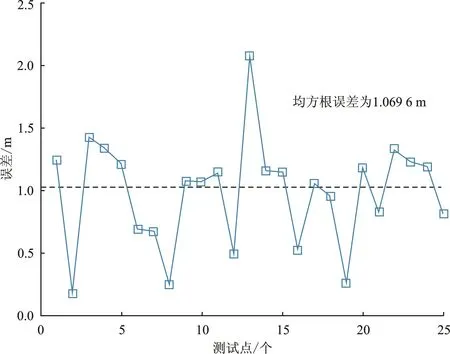
(b) 定位误差
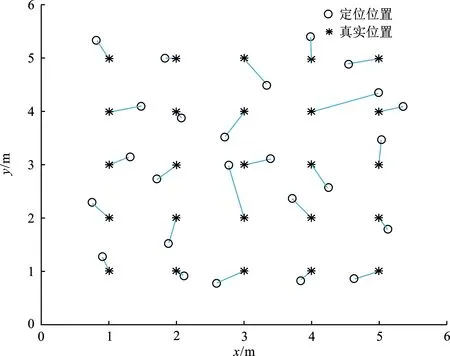
(a) 定位位置与真实位置直线距离

(b) 定位误差
为了比较不同算法的性能,选择指纹定位中常用的K最邻近算法和支持向量机(Support Vector Machine,SVM)方法以及文献[3]和文献[9]中的方法与文中方法进行比较。同样在测试区1的25个位置参考点进行定位计算,并与全站仪测得的真值点进行比较。图7是定位直线距离误差,图8是误差的累积分布函数(Cumulative Distribution Function,CDF)。可以看出,文中方法的均方根(Root Mean Square,RMS)误差为0.485 0 m,最大误差为1.06 m,其中92%优于1 m。对比实验表明,文中方法比其他方法具有更高的定位精度。详细的误差分析如表2所示。
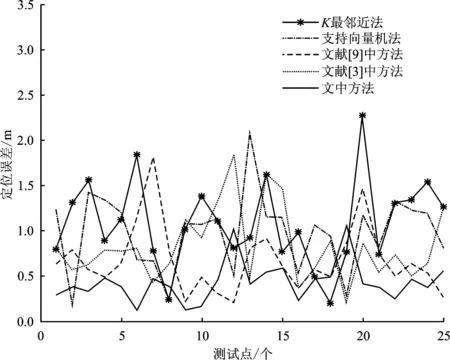
图7 不同定位算法的定位误差

表2 不同指纹定位算法的定位精度比较
3.4 指纹未采集区域定位结果
图9为测试区2定位测试结果,均方根定位误差约为1.123 7 m,平均绝对误差约为0.372 8 m。结果表明,仅依靠仿真计算生成的指纹定位数据可完成粗略定位。由于传统基于实测指纹的定位方法在未采集指纹的情况下将无法进行定位,基于仿真指纹可完成粗精度初步定位,与传统方式相比有很大改进与提升。本实验采用了间隔为0.5 m的100个模拟采样点,若想得到更高精度的定位结果,则可在计算机可承载前提下适当加大采样点密度。

(a) 定位位置与真实位置直线距离
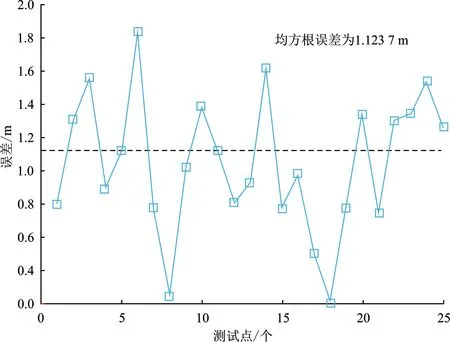
(b) 定位误差
4 结束语
文中提出了一种基于射线追踪和人工神经网络的室内伪卫星混合指纹定位方法。该方法根据室内大型场景的定位需求,利用确定性建模生成的指纹特征参数,对人工神经网络的输入数据集进行扩展。测试环境搭建在某机场到达厅,利用卫星导航系统与装备技术国家重点实验室研制的伪卫星定位终端对该方法的定位性能进行了测试验证。结果表明,在实际采集指纹的区域定位精度有所提高,在未采集指纹的区域也可以完成初步定位。
目前的工作还比较初步,主要是因为模拟和测量的信道状态信息数据特征不够多样化。在未来的工作中,可以分析应用更多的信道状态信息特征,例如到达角观测量和多普勒观测量,并应用于动态定位测试,以提高大型场所的行人定位精度。

