输电线路有覆盖土层嵌岩桩水平位移计算

杨卓帅

（中国电建集团福建省电力勘测设计院有限公司 福建福州 350003）

0 引言

随着我国电网工程建设的快速发展，输电线路途经的山地地形占比越来越多，输电线路基础承受的杆塔荷载也越来越大，当山区中遇到各类风化岩石地基时常采用挖孔基础。因山区岩石层上部覆盖土层厚度的差异，造成挖孔基础竖向承载力和桩土侧向力产生的影响较大。对于基岩直接出露和基岩上覆一定厚度土层2 种赋存形态的山区岩石地基，将岩石挖孔基础分为岩石嵌固基础和嵌岩桩2 类。

输电线路嵌岩桩是指无覆盖土层或者有覆盖土层且桩端嵌入一定深度基岩的挖孔基础，宜采用等直径直柱型式且埋深一般较大。嵌岩桩基的开挖主要利用机械（人工）在天然原状岩土体中钻（挖）出基础设计形状的基坑，在基坑内设置筋骨架、预埋地脚螺栓或其他类型的连接件，以天然岩土体代模在基坑内直接浇筑混凝土，形成钢筋混凝土基础体。基坑没有支模、地基岩土体回填等作业工序，可有效避免施工过程的大开挖，因而具有工程施工进度快、基础材料省、工程造价低等优点，具有较好经济和环境保护效益，属于环保型基础型式之一。

本文综合建筑、港口、公路、铁路等行业嵌岩桩工程设计方法和宝贵经验，结合山区输电线路基础特点，对比各方式的计算结果，分析现行输电线路有覆盖土层的嵌岩桩基础水平位移公式的适用范围，研究成果可为我国山区输电线路嵌岩桩基础设计提供借鉴。

1 嵌岩桩水平位移的计算理论

输电线路基础在承受较大竖向力荷载外，往往还需承受一定的水平荷载。桩基的水平承载力不仅与桩本身材料强度和截面有关，且很大程度取决于桩侧土的水平抗力。现行的《输电线路岩石地基挖孔基础工程技术规范》（DL/T 5845—2021）（以下简称电力岩规）的嵌岩桩基础在水平荷载作用下基顶水平位移的解析计算方式依据地基覆土情况划分为无覆盖层嵌岩桩和有覆盖层嵌岩桩2 种情况。

1.1 有覆盖土层嵌岩桩水平位移计算

参照国外学者Carter 和Kulhawy 研究成果，将有覆盖层嵌岩桩在土岩界面处分解成覆盖土层中悬臂段桩身和基岩中嵌岩段，相应的水平承载力计算模型参照图1。嵌岩桩基顶水平位移按土岩界面分段计算后叠加，如式（1）。

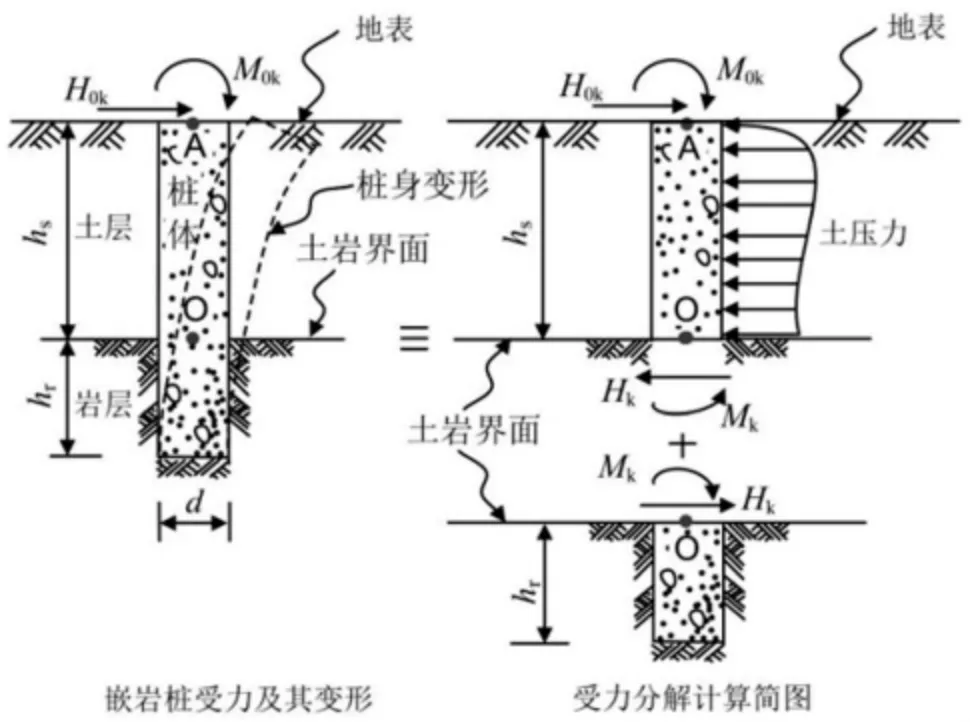
图1 嵌岩桩水平承载力计算模型

式中：桩身变位uao为覆盖土层引起的桩基设计地面处水平位移值；u 和θ 分别为基岩中嵌岩段在土岩界面处的水平位移和转角。

1.2 电力岩规中嵌岩桩的uao、u 和θ 取值

考虑覆盖层土作用的嵌岩单桩水平位移计算，将上部覆盖土层悬臂段桩身假定桩侧向土处于极限平衡状态，地基反力按直线分布，桩侧压力由土的粘结作用和摩擦作用两部分组成，参照图2 所示计算模型分析。悬臂段桩身水平位移uao按式（2），土岩界面处桩身内力则截取悬臂段桩身单独分析。将桩基嵌岩端作为固接约束条件考虑，则土岩界面处桩身水平力及弯矩标准值的计算公式分别为式（3）和式（4）。

图2 覆盖土层桩侧土压力分布与计算模型

式中：Hk为嵌岩单桩土岩界面处桩身截面水平力标准值；Mk为嵌岩单桩土岩界面处桩身截面弯矩标准值；（EI）p为嵌岩段桩身计算抗弯刚度；Hok为嵌岩单桩基岩顶面处桩顶水平力值；Mok为嵌岩单桩基岩顶面处桩顶截面弯矩值；cu为覆盖土层桩侧土体不排水剪切试验的黏聚强度；γs为覆盖土层土体容重；Kp为覆盖土层桩侧土体侧向土压力系数，Kp=（1+sinφ）/（1-sinφ）；hs为桩覆盖土层厚度。

下部嵌岩段水平承载性能计算模型参照图3。桩体在土岩界面处的水平位移和转角，引用电力岩规5.3.1、5.3.2 条文说明表13，依据嵌岩单桩的深径比hr/d 对桩身水平承载性能状态按式（5）进行划分，存在柔性、刚性、中间状态3 种情形。对柔性和刚性承载性能状态的土岩界面处u、θ 值分别按照式（6）和式（7）进行计算，介于两者之间的中间状态取2 种结果中较大值的1.25 倍。

表1 基础荷载设计值 单位：kN

图3 岩层段单桩水平承载性能计算模型

式中：G*为桩周岩体等效剪切模量；Ee为桩身等效弹性模量；hr为桩嵌入基岩深度。

1.3 建筑、港口、公路、铁路等行业规范中嵌岩桩uao、u 和θ 取值

上部覆盖土层悬臂段水平荷载作用下基桩的受力，在建筑、港口、公路、铁路等行业规范中，通常根据桩-土相对刚度将桩划分为刚性桩和弹性桩。当桩身无量纲入土深度时，桩身刚度较大，可不考虑水平荷载下桩身的挠度变形，划为刚性桩；当时，桩的相对刚度较小，桩身挠曲变形较大，划为弹性桩，其水平承载力取决于桩材抗弯刚度和桩侧土强度。对应的基顶位移uao分别采用刚性桩和弹性桩计算原理进行对比分析。

根据桩身无量纲入土深度αh 划分：

（1）αh≤2.5 的刚性桩，采用极限地基反力法。对支承在岩石上的刚性桩位移及作用效应进行分析。将地基土为弹性变形介质体，假定不考虑桩土与土体的粘聚力和摩阻力，以及桩-土刚度视为无限大2 种状态，推导覆盖土层段的受力情况如图4。覆盖土层水平位移uao如式（8），u、θ 值则采用式（9）和式（10）计算土岩界面处桩身水平力及弯矩值，代入上述式（5）～（7）得出。

图4 支承在岩石上的刚性桩的计算图示

式中：m 为地基抗力系数的比例系数；ω 为覆盖土层悬臂段基础转角；D0为规范中表内系数。

（2）αh＞2.5 的弹性桩，采用弹性地基反力法。假定地基为服从虎克定律的弹性体，地基反力与桩上任一点的位移成正比，引用我国目前应用最多的m 法计算。将土体假定为弹性体，用梁的弯曲理论求解桩的水平抗力。含覆盖土层水平位移uao按式（11），土岩界面桩身内力采用式（12）和式（13），并代入上述式（5）～（7）得出u、θ 值。

式中：A4、B4、C4、D4为规范中表内系数。

下部嵌岩段土岩界面处的基桩变位，在基岩中的嵌岩桩长符合最小嵌岩深度内，岩层段内的桩身变位极小，直接引用电力岩规中无覆盖土层的嵌岩单桩水平位移计算模型进行对比分析。公式中涉及的桩身土岩界面水平力、弯矩等内力值则依据刚性桩、弹性桩的计算理论获得。

2 嵌岩桩水平位移算例分析

某特高压工程实际荷载条件，基础荷载设计值如表1。

假设塔位地形为平地条件，地层分布及岩土体设计参数如表2～4 所示。

表2 覆盖土层地质参数－黏性土

表3 岩层地质参数－凝灰岩

表4 桩身及过程参数

根据表1～4 所列的设计参数，并取覆盖土层0.5～12 m，按0.5 m 极差递增。在满足承载力及最小嵌岩深度的要求内，采用上述3 种水平位移的设计原则，计算出嵌岩桩基顶水平位移与桩身无量纲入土深度αh 间的对比关系图，如图5（a）所示。

图5 水平位移对比图

从图5 可以看出，在工程实例中，桩身无量纲入土深度αh＜2.0 范围内，采用支承在岩石上的刚性桩理论计算出的嵌岩桩基顶水平位移与电力岩规的计算结果比较接近。当αh＞2.0 之后，电力岩规的嵌岩桩基顶水平位移与刚性桩和弹性桩的水平位移数值出现了过度偏差，同样土岩界面处的桩身内力也出现较大差异，且αh 值越大，偏差值越大。为进一步分析桩基水平位移设计方式的适用性，各选取110、220、500 kV 通用设计中某塔型，依据表2～4 的地质参数进行分析，各杆塔的基础荷载设计值见表5。

表5 基础荷载设计值 单位：kN

图5（b）～（d）分析得出杆塔荷载的变化对电力岩规中嵌岩桩的水平位移设计原则适用性无较大影响。电力岩规中假定嵌岩桩侧土体处于极限平衡状态，不考虑桩身与地基的变形特性的方式。采用直线型地基反力分布方法所推求的桩身受力情况以及水平位移计算公式具有一定的局限性。若按桩的无量纲入土深度αh 来划分，较适用于αh＜2.0 的刚性短桩。当αh＞2.0 时，与建筑、港口、公路、铁路等行业规范中刚性桩、弹性桩的设计原则对比，含覆土土层的基顶水平位移计算结果出现差异较大，且土岩界面处桩身内力也存在此类情况。当土岩界面的桩身弯矩起主要控制作用时，进而会影响桩身截面受弯、受剪承载力及配筋等设计。

3 结语

本文主要论述针对我国山区输电线路应用岩石地基挖孔基础中嵌岩桩的水平位移计算方法。结合建筑、港口、公路、铁路等行业的经验和规范，对电力岩规中含覆盖土层嵌岩桩的水平位移计算结果进行了对比分析。利用各计算理论适用范围的不同，可更好地服务于输电线路嵌岩桩基础在水平位移计算中的性能要求。

基于本文提出的对比结果表明，电力岩规中含覆盖土层的嵌岩桩基顶水平位移设计原理及计算公式较适用于αh＜2.0范围内的刚性短桩。但当αh＞2.0 时，建议根据实际情况采用建筑、港口、公路、铁路等行业规范中刚性桩或弹性桩的水平位移及作用效应作为补充计算，提高基础设计的合理性。