基于水文学模型的洞庭湖内部超额洪量分布

宋 雯,王加虎,卢金友,赵文刚,刘晓群

(1.湖南省水利水电科学研究院,长沙 410007; 2.河海大学 水文水资源学院,南京 210098;3.长江科学院 水利部江湖治理与防洪重点实验室,武汉 430010)

0 引 言

一直以来长江中下游防洪问题受到广泛关注,俗有“万里长江,险在荆江,难在洞庭”之说[1]。长江中游洪水峰高量大,与河道泄洪能力不足的矛盾突出,城陵矶附近形成巨大的超额洪量。洞庭湖是长江中游主要调蓄湖泊,1954年长江流域发生特大洪水,洞庭湖天然湖泊调蓄容积达170亿m3[2],发挥了明显的调洪蓄洪作用。随着长江上游梯级电站相继建成,三峡水库对城陵矶防洪补偿潜力增大,水库群对上游洪水调蓄能力进一步增强,长江中下游防洪情势得到改善。但是现状情况下重现1954年洪水,长江中游城陵矶附近仍存在200亿m3超额洪量[3],充分发挥洞庭湖的滞洪功能与蓄洪作用十分迫切。

采用水文学方法模拟长江中下游极其复杂的江河水网洪水演进,可以计算控制站的安全泄量或者控制水位下各个河段的超额分洪量,在长江干流宜昌、螺山、汉口、大通等主要控制站点的水位、流量模拟计算方面都取得了较好的效果[4-9]。洞庭湖作为中国第二大淡水湖,湖区跨度大,集雨面积广,水系复杂,洪水问题突出,以往关于洞庭湖内部洪水规律研究的成果较少,内部洪水演进的研究还有待深入。本研究基于水文学方法,采用大湖总分结构,建立西、南、东洞庭湖分区域洪水水文模型,探索洞庭湖内部洪水演进规律,定量评估特征洪水条件下的湖区内部超额洪量分配规律,进一步为长江、洞庭湖流域防洪规划与布局提供技术参考。

1 研究区域概况

自枝城至城陵矶河段为著名的荆江,两岸平原广阔,地势低洼,其中下荆江河道蜿蜒曲折,素有“九曲回肠”之称,南岸有松滋、太平、藕池、调弦(已封堵)四口分流入洞庭湖,由洞庭湖汇集湘资沅澧四水调蓄后,在城陵矶注入长江,江湖关系最为复杂[8],江湖洪水相互依托,历来是长江流域重点防洪地区。本文以枝城至螺山段为计算范围,考虑荆江三口、湘资沅澧四水,研究洞庭湖内部超额洪量分配情况,对比蓄洪垸蓄洪容量,探讨洞庭湖湖区防洪布局现状。

2 模型构建

2.1 模型原理

洪水水文模型基本依据是圣维南方程组,即

(1)

(2)

式中:u为流速(m/s);A为过水断面面积(m2);y为水位(m);g为重力加速度(m2/s);x为沿河长度(m);t为时间(s);Q为流量(m3/s);K为流量模数。

全解圣维南方程组需要较高精度的基本资料。可以采用水文学的经验槽蓄曲线方法[10],即在一定条件下,将连续方程(1)简化为河段水量平衡方程,将动力方程(2)简化为槽蓄方程,得到:

Idt-Qdt=dW;

(3)

W=f(Q,I) ;

(4)

Q=f(z) 。

(5)

式中I、Q、W、z分别代表河段的入流量、出流量、槽蓄量、水位。

演算时采用河段槽蓄和以水位日涨率、下游顶托、起涨水位为参数的水位-流量关系曲线[11],将式(3)改写为

(6)

式中:I1、I2分别为时段始末的入流量;Q1、Q2分别为时段始末的出流量;Δt为时间(d);W1、W2分别为时段始末的槽蓄量。

具体计算时将式(6)化为

(7)

根据I1、I2和初始水位H1,调用有关演算曲线计算

(8)

然后假定时段末水位H2,调用有关演算曲线计算

(9)

若

|M*-M|<ε。

(10)

式中ε为允许误差限。则认为Q2和H2是所求的时段末值,否则采用二分法进行迭代计算。

洞庭湖洪水水文模型在求解过程中,根据水量平衡原理,将入流量、出流量及槽蓄量的变化组成湖泊水量平衡体系,应用容积曲线进行调洪演算,得到螺山站的水位过程[6]。因其受湖区地形、螺山站断面等影响,本研究选用非线性水库方程简化版修正出流曲线[12],即任意时刻槽蓄量W和出流量Q符合式(11)关系,即

(Qj+1Δt)m=Wj+1k。

(11)

式中:k为出流系数,k∈(0,1];m为指数,m∈(0.6,1];j和j+1表示相邻的前后时段

将式(11)的Wj+1代入式(6)后整理得到

式中除了Qj+1外,全部是已知量。非实时预报条件下Q∈(0,Imax],可以用二分法求解;实时预报时,Q的上限取历史极值。对于初始出流量Q0,可以直接等于I0,这意味着模型计算时要从一个流量平稳的低水段开始,符合水文计算的习惯。

2.2 计算范围

本文构建了洞庭湖洪水水文模型,模拟范围为长江干流枝城至螺山段、洞庭湖四水尾闾入湖控制站以及荆江三口所围区域。根据中下游流域防洪及分洪特点、洞庭湖地理特性,将模拟范围细分为若干个小湖进行计算(见图1),其中,城陵矶附近超额洪量由长江-洞庭湖-螺山出口计算结果确定,上边界取枝城、石门、桃源、桃江、湘潭站为入流站,出流站为螺山站;洞庭湖分蓄洪总量由荆南三口湘资沅澧四水-七里山出口站计算结果确定,上边界以沙道观、新江口、弥陀寺、藕池康、藕池管、石门、桃源、桃江、湘潭站九站为入流站,出流站为七里山站;洞庭湖主体水域已经分割为东洞庭湖、南洞庭湖以及西洞庭湖,结合水量平衡原理及水流方向,湖区内部西南洞庭湖或东洞庭湖分蓄洪总量以鹿角为出口站计算结果确定,上边界以沙道观、新江口、弥陀寺、藕池康、石门、桃源、桃江、湘潭七站为入流站,出流站为鹿角(鹿角为水位站,考虑其与七里山流量关系,因此Q鹿角=Q七里山-Q藕池管);西洞庭湖分洪总量为南咀+小河咀出口计算结果之和确定,其中目平湖入流比例为I南咀∶I小河咀=4∶6,该公式经验性较强。上边界取沙道观、新江口、弥陀寺、石门、桃源站为入流站,出流站为南咀站与小河咀站;南洞庭湖所需分洪量为总区间与东西部分洪量之差得到。具体分配见表1。

表1 各区域计算范围统计

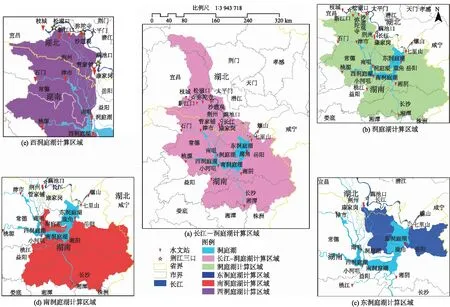
图1 计算区域示意图

2.3 模型率定与验证

通过采用1996年、1998年、2017年实测资料进行验证,选用SCE-UA(Shuffled Complex Evolution)算法[13-14]进行参数优选求得全局最优解,模型的可信度采用纳什系数[15](N)进行判断,计算公式为

(3)

根据计算要求,模型输入洞庭湖1996年、1998年和2017年典型洪水,在区域边界出口螺山、七里山、鹿角、南咀、小河咀共5个测站输出水位、流量率定结果(见图2)。结合表2和表3可以看出,螺山站的拟合效果明显优于湖区内部各控制站,1996年、1998年、2017年水位、流量曲线拟合效果均较为可靠,分析其原因,螺山为长江干流主要控制站,水力学条件相对稳定,总水量偏大,来水、出水变化接近水量平衡。而湖区内部七里山站为洞庭湖出口控制站,受长江干流段顶托作用明显,遭遇1998年全流域型洪水时,水位、流量曲线拟合表现劣于螺山站,流量拟合纳什系数<0.9。由于鹿角站流量为计算后流量,其水位、流量拟合曲线与七里山站较为接近,南咀、小河咀总水量相对较小,受顶托和湖泊滞蓄的影响较大,水位、流量曲线拟合程度受入湖来水影响明显。另外,对比1996年、1998年、2017年3个年份的率定结果,1996年沅江和资水出现罕见洪水,水位涨幅变动大,西南洞庭湖对南咀、小河咀存在洪水顶托作用,导致南咀与小河咀站水位拟合纳什系数均<0.85,水位率定结果较差。1998年湖区内其他各站水位、流量较1996年均表现较差,产生该现象的原因:一是1998年洪水为全流域型洪水,湖区内部各区域洪水顶托作用较大;二是洪量规模较大,超出模型设定目平湖调洪比例,进而导致南咀、小河咀拟合效果较差。2017年洪水是以洞庭湖来水为主的特大洪水,因螺山泄流顺畅,且湖区内部受荆江三口影响较小,故该年份率定结果较为可观。尽管在各站点局部水位存在差异,但整体上验证结果较好,其涨落过程和洪峰计算值与实测资料吻合较好。

表2 模型计算误差分析——水位

表3 模型计算误差分析——流量

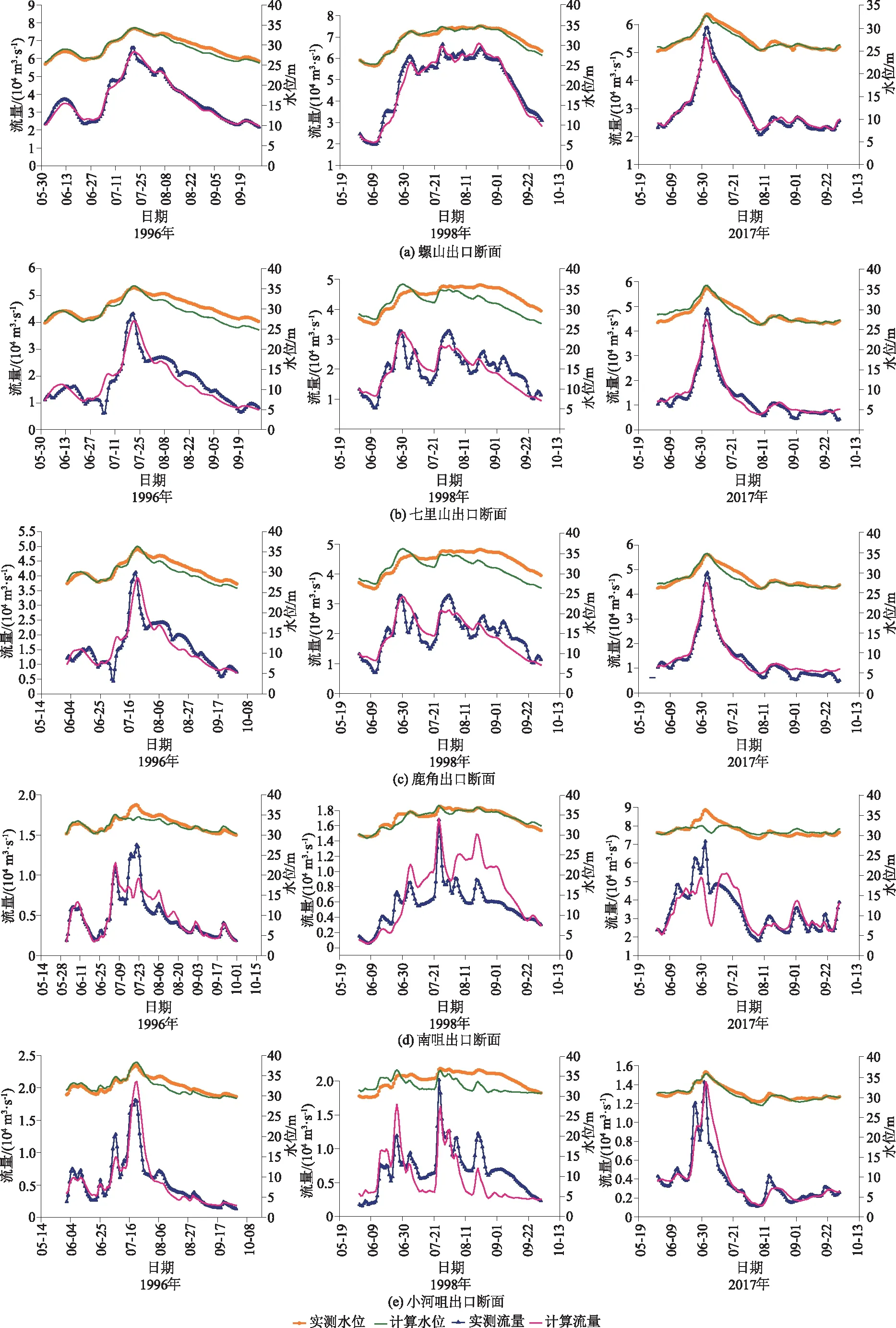
图2 1996年、1998年、2017年研究区域各出口断面水位、流量率定结果

2.4 典型年水位-流量统计

结合1954年、1996年、1998年、2017年典型年洪水、长江及洞庭湖各个控制站点水位-流量实测资料,分别对城陵矶(莲花塘)防洪控制水位34.40 m对应的平均泄流能力、年最高水位、年最大流量进行了统计,结果如表4所示。

表4 洞庭湖主要控制站水位、流量统计

3 计算结果与讨论

3.1 三峡水库调蓄作用对城陵矶附近超额洪量的影响

为了模拟不同地形条件下的洪水分配情况,分别选取1996年(三峡水库建成以前)、1998年(三峡水库开始拦水)和2017年(三峡水库建成投入使用以后)水文实测数据率定参数,输入1954年实测洪水系列和三峡水库调度运用后的1954年洪水系列,模拟计算三峡水库至洞庭湖区间枝城—螺山出口城陵矶附近超额洪量。

本文分别以城陵矶(莲花塘)实际控制水位34.40 m、提高城陵矶(莲花塘)控制水位至34.90 m,以及按照长江流域防洪规划一直采用的65 000 m3/s泄流能力3个控制条件计算三峡调度前后的1954年从枝城演进到螺山的洪水,得到结果见表5。三峡水库调蓄、抬高0.5 m防洪设计水位、增大泄流能力3项措施均可不同程度降低城陵矶附近超额洪量,其中,1996年与2017年螺山泄流能力较大的条件下,三峡水库调洪作用(42%～45%)高于城陵矶控制水位抬高0.5 m(即莲花塘控制水位为34.9 m)(30%～31%)与增大螺山泄流能力调洪作用(34%～38%),而1998年由于全流域洪水,螺山站受下游洪水顶托,在洪水拥堵不畅的条件下,三峡水库调洪作用(45%)低于增大螺山泄流能力调洪作用(53%)。该结果说明,螺山泄流能力为城陵矶超额洪量的决定因素,洞庭湖洪水受长江洪水影响较大。

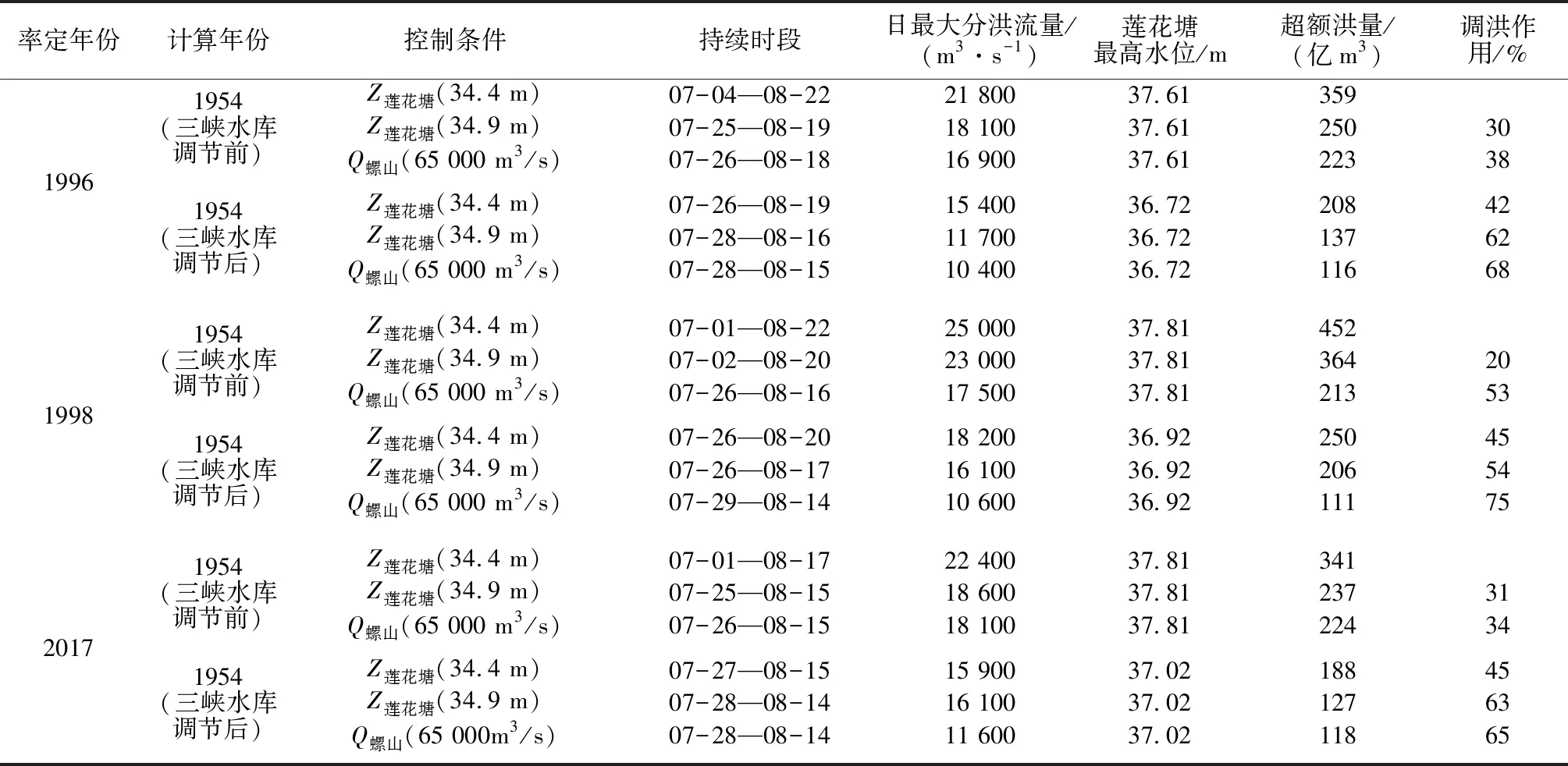
表5 不同泄流条件下三峡水库调蓄作用对城陵矶附近超额洪量分配的影响

3.2 洞庭湖区防洪蓄洪能力分析

根据洞庭湖目前的水利工程分布情况(见图3),西、南、东洞庭湖均建有蓄洪垸以满足蓄洪要求(见表6):西洞庭湖蓄洪垸可蓄洪总量为13.15亿m3,南洞庭湖蓄洪垸可蓄洪总量为53.09亿m3,东洞庭湖蓄洪垸可蓄洪总量为48.08亿m3[16]。

表6 洞庭湖湖区蓄洪垸蓄洪量

图3 洞庭湖蓄洪垸示意图

为了讨论洞庭湖区内部洪水演进过程,本文分别以洞庭湖区间荆江三口四水-七里山出口、西南洞庭湖区间太平、松滋、沅江、澧水-鹿角出口、南咀区间太平、松滋、澧水-南咀出口、小河咀区间沅江-小河咀出口模拟计算3种洪水条件下洞庭湖、西洞庭湖、南洞庭湖、东洞庭湖遭遇典型洪水时各个区域需要承担的超额洪量(见表7)。

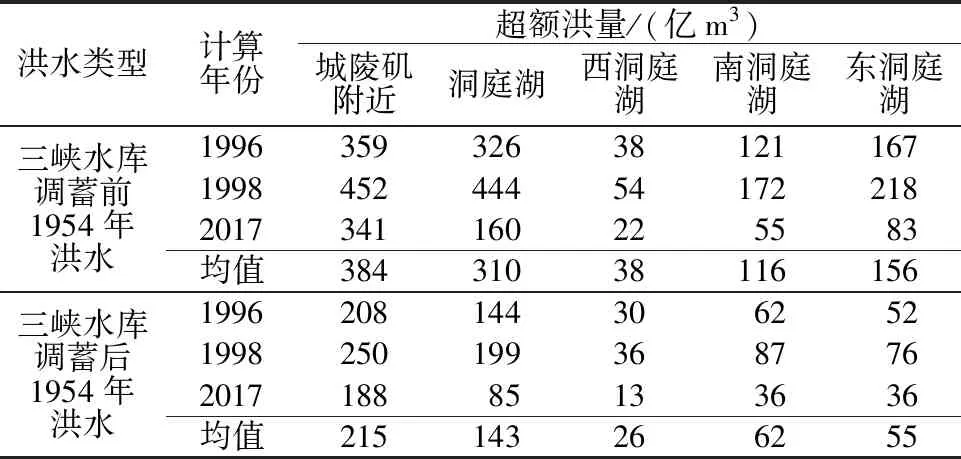
表7 三峡水库调蓄前后长江-洞庭湖区超额洪量分配情况

对比模型计算结果,三峡水库调蓄前,1996年、1998年边界条件下,以七里山为出口的洞庭湖内部超额洪量(326亿、444亿m3)接近城陵矶附近超额洪量总量。这是由于长江洪水枝城下泄流量至螺山比重较大,遭遇洞庭湖洪水,导致七里山受顶托作用较大,泄流能力分别为34 100、26 500 m3/s,湖水下泄不畅,超额洪量总量较大。而2017年洪水主要集中于洞庭湖,枝城下泄流量较小,七里山泄流能力达到47 900 m3/s,洪水由七里山宣泄至螺山,湖区内部滞蓄洪水较少,因此超额洪量明显低于以上2个年份。三峡水库调蓄后,湖区内部超额洪量减少程度在50%以上,平均条件下,西、南、东洞庭湖超额洪量分别为26亿、62亿、55亿m3,大于湖区现有蓄洪垸可蓄洪总量。

3.3 讨 论

三峡水库调蓄前,遭遇1954年洪水,枝城站最大下泄流量达到70 300 m3/s,城陵矶附近1996年、1998年、2017年分别存在359亿、452亿、341亿m3超额洪量,洞庭湖分别存在326亿、444亿、160亿m3超额洪量。可以看出,洞庭湖洪量的变化主要与七里山泄流能力相关。1996年干流顶托严重,七里山站平均泄流能力较小,为34 100 m3/s,该条件下遭遇1954年型洪水,洞庭湖洪量等于或超过城陵矶地区洪水总量,2017年七里山泄流能力增加至47 900 m3/s,洞庭湖洪量减少为城陵矶地区洪水总量的1/2。

三峡水库调蓄后,城陵矶附近超额洪量从384亿m3减少至215亿m3(平均条件下),洞庭湖超额洪量从310亿m3减少至143亿m3(平均条件下),湖区内部东洞庭湖较南洞庭湖与西洞庭湖减少程度多。一方面是三峡水库调蓄使长江干流下泄流量减小,入湖水量减少;另一方面是螺山下泄顺畅,东洞庭湖洪量容纳总量降低。另外,从表5也可知,当城陵矶水位抬高至34.9 m或者螺山泄流能力达到65 000 m3/s时,经三峡水库调蓄后洞庭湖超额洪量总量减少程度也大幅提高。总体上可知,经三峡水库调蓄后,高水位洪水持续时间缩短,日最大分洪流量减少,超额洪量总量减少,三峡水库洪水调蓄作用明显。

4 结论与建议

洞庭湖与长江形成复杂的江湖关系,湖区水系交错,河网复杂,基于水量平衡的水文模型可模拟复杂来水条件下单一出口控制断面水位流量关系,研究选取了1996年、1998年、2017年3种不同类型洪水简化螺山站水位-流量关系,再现了1954年洪水江湖洪量分配情况,得出以下结论:

(1)三峡水库投入使用以前,遭遇1954年洪水,城陵矶地区存在约384亿m3超额洪量;三峡水库投入使用以后,相对于城陵矶34.4 m防洪水位时,超额洪量减少至215亿m3,调洪作用在44%左右。现有江湖关系遭遇1954型大洪水时,在以2017年洪水为代表的螺山顶托不严重的条件下,洪水下泄顺畅,洞庭湖内部超额分洪任务会大幅减少;而在以1996年、1998年洪水为代表的长江来水较大的情况下,螺山受下游洪水顶托,洪水下泄不畅滞留于洞庭湖区,洞庭湖控制区间需要承担的超额洪量接近城陵矶附近超额洪量。

(2)总体上可以看出,三峡工程建成后,长江中下游防洪形势得到较大改善,中下游超额洪量大幅减少。但是,遭遇长江目标洪水1954年型洪水时,增大螺山泄流能力并配合蓄滞洪区运用,仍有部分洪水未能得到有效安置,需要抬高部分河段运行水位或者加大螺山泄流能力,才能保证长江中下游河段行洪安全。