非线性振动系统的多项式向量方法1)
金栋平
(南京航空航天大学航空航天结构力学及控制全国重点实验室,南京 210016)
引言
非线性振动系统近似解法主要有基于派生系统解特征而衍生出的方法,如平均法等,以及基于摄动展开的方法,如Lindstedt-Poincaré方法、KBM 法、多尺度法和源于滤波的方法,如谐波平衡法等[1-5].学者们采用上述方法成功揭示了工程非线性振动中的复杂动力学行为,如滞后非线性中的分岔[6]、相轨线跳跃现象[7],并用于非线性隔振器设计[8]等.现代工程结构和系统大多带有柔性附件、振动控制器[9],使得受控动力学模型表现为很高维数之特征.借助动力学等效等模型进行降阶,可以大大降低动力学模型的维数[10-11],使得由周期单元组成的复杂结构非线性振动能够进行半解析和半数值分析[12-13].然而,当非线性振动系统的维数较高时,上述摄动方法、多尺度方法等需逐步、依次求解微分方程组,加上计算机符号软件可以不支持海量指数的提取[14-15]等运算,需要人工参与,以致工作量巨大、计算效率低.
本文针对高维非线性振动系统的近似求解问题,通过常数矩阵和多项式向量函数的乘法,将非线性部分表示成为矩阵和向量积形式,以致幂次近似解均满足一组非齐次状态方程,进而根据一阶非齐次方程组的求解方法,一次性地获得全部的解析解.由于带有小参数的多项式向量函数之间的乘法运算可以借助Toeplitz 矩阵表示成矩阵之间的乘法运算,借助计算机符号软件等工具可以实现计算过程的程序化.最后,通过一个四维弹簧摆振动的算例,展示了多项式向量方法在解决高维非线性振动时的可行性.
1 多项式向量
研究n维非线性振动系统,状态方程为
一般地,可以将方程(1)写成多项式向量形式
其中,k次齐次多项式向量函数为
式中,ei=[0 0···1···0 0]T表示第i列元素为1 的单位向量,mi为非负整数.
若采用摄动法,将
代入方程(4)并比较方程两边 ε同次幂系数,得
2 多项式乘法
定义T阶滞后算子
该算子由单位矩阵IT=[e1e2···eT]通过消去第一列并在最后一列添加零列向量形成,在次对角线上的元素为1、其余均为0.此外,左下角元素为1;对r≥0,.例如
利用上述滞后算子,可以将多项式相乘转换成Toeplitz 型下三角矩阵的乘法形式.将小参数视为变量,令
则
因而
即x1(L4)x2(L4)第1 列元素χ(q)正是两个多项式相乘后的 εq次幂的系数.根据方程式(5),第k次齐次多项式函数的 εq次幂的系数为
式中,T=q+1.依据式(16),即可确定方程式(7)~式(10)中任意次幂系数的多项式函数,继而依次求出各阶近似解.
类似地,有
可见,非线性振动系统中齐次多项式乘法运算可以转换成一系列Toeplitz 矩阵的乘法运算,以致原本繁琐的逐个摄动求解转变为一系列矩阵形式的非齐次方程求解问题.这样做的好处就是,对于高维非线性振动系统,借助计算机符号软件对于多项式向量函数和矩阵运算的优势,通过多项式矩阵乘法的运算,无需对二阶微分方程逐个求解,从而一次性地获得形式上结构简洁的全部近似解.值得注意的是,直接摄动法得到的解在t∈[0,1/ε]内有很好的近似.
3 算例
(1)算例1
首先,考虑二维平方非线性振动系统
根据式(16),有
故
因而,一次近似解为x=x(0)+εx(1),该结果与文献[4]直接摄动法给出的结果相同.可以继续求满足初始条件的二次幂方程的解,即
可见,借助Maple 等计算机符号软件工具,上述建立在多项式向量求解方法上的矩阵运算程序很容易编写和执行.注意到,式(28)中出现了九期项tsint.下面研究更高维数的非线性振动问题.
(2)算例2
考虑静平衡位置附近弹簧摆的面内微振动,此时近似到二阶的非线性振动方程为
写成状态方程形式,令x=x1,=x2,y=x3,=x4,有
根据式(16),对于二次近似解,有
为简洁起见,取 ω=1,有
将式(30)和式(32)代入式(36),得到二次幂方程的解析表达式.为简洁起见,取 α=1,β=2,则
因而,二次近似解为x=x(0)+εx(1)+ε2x(2).注意到,式(37)中出现了九期项tsint和tcost.

图1 近似解析解与数值结果对比(=[0.01 0 0.01 0]T)Fig.1 Comparison of the proposed method and simulation results for the differential small parameters (=[0.01 0 0.01 0]T)
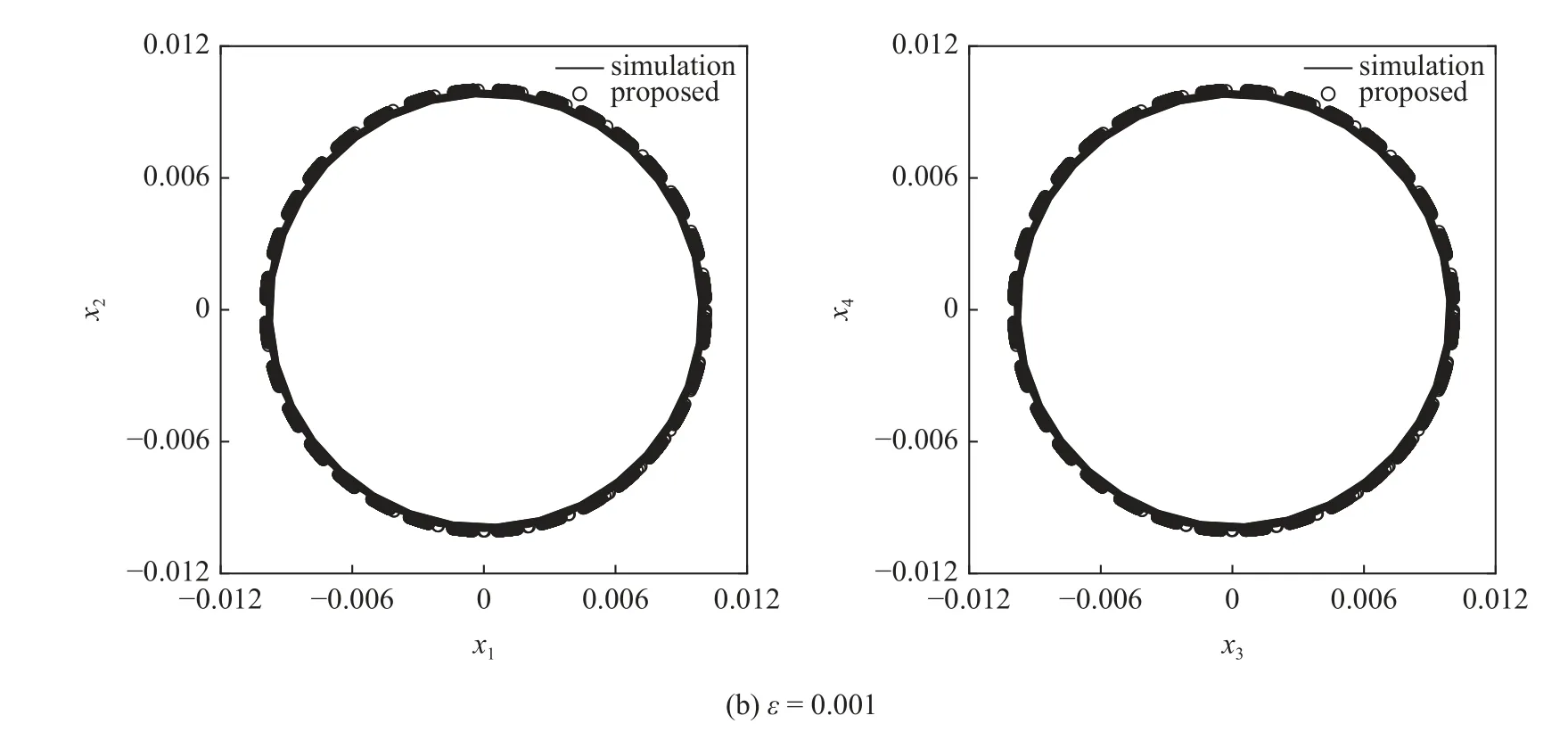
图1 近似解析解与数值结果对比(=[0.01 0 0.01 0]T)(续)Fig.1 Comparison of the proposed method and simulation results for the differential small parameters (=[0.01 0 0.01 0]T)(continued)

图2 近似解与数值结果对比(=[0.1 0 0.1 0]T)Fig.2 Comparison of the proposed method and simulation results for the differential small parameters (=[0.1 0 0.1 0]T)
4 结论
对于齐次多项式作为非线性的高维振动系统,可以通过多项式向量将非线性部分表示成常数矩阵和多项式向量之积,进而将非线性振动系统表示成一系列矩阵和向量的乘积形式.在采用基于摄动展开的方法时,小参数作为幂级数出现,因而可以采用Toeplitz 矩阵实现幂次近似解作为元素的多项式之间的乘法运算.因此,非线性振动系统的解完全由矩阵和多项式向量之间的乘法运算获得,从而有望解决高维非线性振动系统的求解难题.

