非厄米哈密顿量中的量子Fisher 信息与参数估计*

李竞 丁海涛 张丹伟†

1)(华南师范大学物理学院,原子亚原子结构与量子调控教育部重点实验室,广州 510006)

2)(南京大学物理学院,固体微结构物理国家重点实验室,南京 210093)

量子Fisher 信息给出参数估计的最优精度极限,在量子度量学中有重要的应用.近年来,在量子系统中实现非厄米哈密顿量的理论与实验研究受到广泛关注.本文研究基于非厄米哈密顿量本征态的参数估计,给出其中单参数与两参数估计的量子Fisher 信息及其量子Cramér-Rao 下界,计算与分析非互易、具有增益-耗散的Su-Schrieffer-Heeger 模型,非厄米量子Ising 链、拓扑陈绝缘体模型和二能级系统中动量及外场参数估计的量子Fisher 信息.结果表明:在这几个非厄米模型中,对于单参数估计,量子Fisher 信息在能隙闭合区域和例外点附近显著增大,从而提高参数估计的精度极限;对于两参数估计,量子Fisher 信息矩阵的行列式在能隙闭合和例外点附近同样明显增大,拓扑区域比平庸区域的整体评估精度更高,且由陈数确定两参数估计误差的拓扑下界.

1 引言

1969年,Helstrom[1]提出量子系统中未知参数的测量精度受不确定性原理的影响,确定了基于量子参数估计的量子度量学的理论基础.在量子参数估计理论中,从给定量子态中提取未知参数的最小误差由量子Fisher 信息描述,最佳测量精度满足所谓的量子Cramér-Rao 下界(quantum Cramér-Rao bound,QCRB)[2-5].因此,如何增大量子Fisher信息从而提高未知参数的估计精度是量子度量学领域的一个重要问题.研究发现,可以通过量子Fisher 信息与量子几何的内在联系,特别是刻画参量空间中两量子态间距的量子度规[6-11],寻找最优化的测量轨迹和评估策略[12-15].利用量子系统特有的量子纠缠性质,用一个初态为纠缠态的探针提取系统的参数信息,也可以提高量子态的量子Fisher 信息[16-18].在具有临界性质的物理系统,当系统靠近临界点时,物理参数的微小变化会导致量子态性质的明显响应,因此可以利用这种临界增强效应来提高参数评估精度[19-21].此外,近期研究表明选取合适初态以及权衡不同参数的测量误差可以提高参数估计的精度[22,23].

另一方面,近年来在经典或量子系统中实现非厄米有效哈密顿量的实验技术蓬勃发展[24-28],引发研究人员对非厄米物理及其应用的广泛兴趣.理论与实验研究表明非厄米系统具有许多重要的物理性质[29,30].例如,在非厄米系统特有的例外点(exceptional point,EP)附近,本征态能量发生实复或虚复转变,此时系统对参数微扰有强烈的响应,因此可以利用EP 点实现高精度传感[31-33].另外,拓扑物态及其量子模拟[34]也从厄米系统推广到非厄米系统[35-44],并涌现系列新奇非厄米拓扑物理及其应用,包括非厄米Bloch 能带[38]与非厄米趋肤效应[39]、非厄米拓扑安德森局域化[40-42]等,以及利用非厄米拓扑边缘态可以实现高精度的量子传感[43,44].因此,基于量子Fisher 信息,研究非厄米哈密顿量中的参数估计及其与非厄米拓扑的内在联系,是当前量子精密测量与非厄米物理交叉研究领域的一个重要课题.

本文研究非厄米哈密顿量本征态的量子参数估计.首先证明在定态条件下,传统量子Fisher 信息的表达式以及单参数估计和两参数估计的QCRB对于非厄米哈密顿量依然成立.其次结合一维非互易Su-Schrieffer-Heeger(SSH)模型、具有增益-耗散的SSH 模型,以及一维非厄米量子Ising 链研究单参数估计,分别计算这3 个非厄米模型中量子Fisher 信息随动量或单个外场参数的变化.结果表明量子Fisher 信息在能隙闭合点和EP 点附近呈现尖峰,其动量空间积分也显著增大,从而提高单参数估计的精度.最后研究二维非厄米拓扑陈绝缘体模型和二能级系统中的两参数估计,此时量子Fisher 信息矩阵的行列式及其动量空间积分在能隙闭合和例外点附近也明显增大,拓扑区域整体评估精度大于平庸区域.结合贝里曲率及其积分给出的陈数,进一步给出两参数估计误差的拓扑下界.

2 非厄米系统中量子态的量子Fisher信息

考虑量子态|ψµ〉依赖待评估参数μ,通常采用正定算符测量的方法进行参数估计.{ 具体过程是将量子态投影到一组正定的完备基底(I 为单位算符),使评估μ转化为测量量子态在一系列x方向上的概率分布Pµ(x)Tr(ρµΠx),其中密度矩阵ρµ|ψµ〉〈ψµ|.选择不同的正定算符测量会得到不同的评估精度,由测量值和实际值之间的方差 Δµ刻画,而方差的下界只由量子态的几何性质确定,即QCRB[2-5]:(Δµ)2≥1/Fµ,其中FµTr(L2µρµ) 是评估μ的量子Fisher 信息,Lµ2(|∂µψµ〉〈ψµ|+|ψµ〉〈∂µψµ|)是对称对数导数算符.对于厄米系统中的量子态,Fµ的表达式可记为[2]:

本质上,评估一个参数的精度正比于参数发生微小变化前后两量子态的“距离”[6],即相邻两个量子态的可分辨度,因此可以从几何的角度理解量子Fisher 信息.定义一个线微元ds(|ψµ〉,|ψµ+dµ〉)||Dµψµ〉|dµ,其中其模方给出参量空间中量子态的量子度规[6],而Fµ4||Dµψµ〉|2等于量子度规的4 倍.因此,Fµ刻画相邻两个量子态|ψµ〉与|ψµ+dµ〉之间的可分辨度,即越大的Fµ表示两量子态之间有越高的分辨度,意味着对未知参数μ的估计精度越高.

比较(2)式和(3)式,可得不等式:

以上结论可推广到多参数评估情况.以两参数{µ,ν}为例,评估误差为 2×2 的协方差矩阵Σµν,相应的评估精度极限由 2×2 的量子Fisher 信息矩阵Fµν刻画.相应的对称对数导数算符Lµ,ν[1]由∂µ(ν)ρ(Lµ(ν)ρ+ρLµ(ν))/2定义,可证明非厄米哈密顿量归一化本征态下,Fµν的矩阵元表达式为(推导过程见附录A)

3 基于非厄米系统的量子参数估计

本节研究几个典型的非厄米模型中量子态的量子Fisher 信息及其参数估计.3.1 节讨论一维非厄米模型中的单参数估计,3.2 节讨论二维非厄米模型中的两参数估计.

3.1 单参数估计

首先考虑一维非互易SSH 模型[39,46,47],其原胞内非互易跳跃强度为t±δ,原胞间跳跃强度为t′.在周期边界条件下,该模型的动量空间哈密顿量为[47]

令t′1 为能量单位,两能带为

其中准动量k ∈[0,2π],则能隙可定义为ΔE ≡mink|E+(k)-E-(k)|.如图1(a)所示,该模型中能隙闭合(ΔE0)对应能带中出现EP 点以及拓扑转变[47].

图1 基于非互易SSH模型的单参数估计(a)能隙ΔE 随t 和δ的变化;(b) δ 0.2时利用右本征矢|ψR〉评估k的量子Fisher 信息 Fk 随k 和t 的变化(上图)及其积分 Mk 随t 的变化(下图实线);(c)利用|ψR〉评估δ时Mδ 随δ 的变化(实线);(d)利用|ψR〉评估t时Mt 随t的变化(实线).图(b)—(d)中的数据点表示利用左本征矢|ψL〉评估k,t 或δ时相应 的数 值结果.图中t′ 1,Fk和Mµ 做对 数处理Fig.1.Single-parameter estimation based on the non-reciprocal SSH model:(a) Energy gap ΔE as functions of t and δ;(b) Fk by the right eigenstate|ψR〉as functions of k and t for estimating k(top) and the integration Mk by|ψR〉as a function of t(solid line in the bottom)with δ 0.2 ;(c) the integration Mδ by using|ψR〉(solid line) as a function of δ for estimating δ;(d) the integration Mt by using|ψR〉(solid line) as a function of t for estimating t.The data points in panels(b)-(d) denote the corresponding numerical results for estimating k,t or δ by using the left eigenstate|ψL〉.t′ 1 is set and Fk and Mµ are logarithmically plotted in the picture.

考虑实部能量较小的归一化本征态|ψ-〉.|ψ〉(无特别说明时默认为右本征矢|ψR〉),首先对参数µk进行评估,其量子Fisher 信息为Fk4(〈∂kψ|∂kψ〉-〈∂kψ|ψ〉〈ψ|∂kψ〉).选取δ0.2 而改变t≥0,可以发现当t0.8,1.2时,在kπ 处出现EP点,对应本征态能量发生虚复转变.在这两处EP 点附近,Fk呈指数增长的趋势,如图1(b)中的上图所示.为表征Fµ在整个动量空间的大小,定义积分.对于µk情况,Mk随t的变化如图1(b)下图中的实线所示.可以看出,Mk在t0.8,1.2 处出现峰值,说明在能隙闭合点附近对参数k的估计具有最高精度.考虑评估参数µδ,量子Fisher 信息及其积分分别为Fδ和Mδ.图1(c)实线给出t0和t0.2时Mδ随参数δ的变化.当t0时,在δ≥0 的区域中只有一个能隙闭合点,对应Mδ在δ1 附近出现尖峰.当t0.2时,在δ0.8,1.2 处能隙闭合,则Mδ出现两个尖峰.考虑评估参数µt时,图1(d)中的实线给出Mt随参数t的变化.类似地,当δ0 和δ0.2时,Mt分别在t1和t0.8,1.2 的能隙闭合点附近呈现峰值,表明量子Fisher 信息在非厄米和厄米(δ0) 系统中的能隙闭合点附近都会指数增大.非厄米系统具有独特的EP点,其附近量子Fisher 信息也会指数增大,从而提供额外的提高参数估计精度的策略.在图1(b)—(d)中,进一步数值验证了对于归一化左本征矢|ψL〉,其量子Fisher 信息和整体评估精度具有与右本征矢|ψR〉相同的特征.原因在于当靠近能隙闭合点或EP 点时,无论对于左本征矢还是右本征矢,系统性质都会随参数的变化而显著变化.图1 结果表明,非厄米系统中本征态在EP 点或能隙闭合点附近的量子Fisher 信息显著增大,从而可以提高未知参数的估计精度.

非互易SSH 模型在开边界和周期边界条件下具有不同的能谱特征[39],因此进一步考虑开边界系统中的参数估计.实空间中N个原胞的非互易SSH 模型的哈密顿量为

图2 原胞数 N 20 的非互易SSH 模型在不同边界耦合常数Γ 下的单参数估计(a)和(b)分别是开边界情况 Γ 0 时本征能量的实部 与虚部随参数t 的变化;(c)为开边界条件下 利用中间 能态|ψmid〉和基态|ψground〉评估参数t 的量子Fisher 信息 Ft 随t的变化,图中EP 表示例外点,GP表示能隙闭合点;(d)和(e)分别是Γ 0.1,0.6 时本征能量实部随t 的变化;(f)和(g)为不同边界耦合常数Γ下Ft随t的变化.图中t′ 1, δ2/3,Ft 做对数处理Fig.2.Single-parameter estimation based on the non-reciprocal SSH model with different boundary coupling coefficients Γ and the unit cell of N 20 :(a) The real part and(b) the imaginary part of the eigen-spectrum as functions of t under open boundary condition with Γ 0 ;(c) Ft as a function of t by the mid-spectrum eigenstate|ψmid〉and the ground state|ψground〉for estimating t with Γ 0.Here EP and GP denote exceptional point and gapless point,respectively;(d) and(e) the real part of energy as a function of t with Γ 0.1,0.6,respectively;(f) and(g) Ft as a function of t different values of Γ.In the figure,t′ 1, δ 2/3,and Ft is logarithmically plotted.

进一步考虑边界耦合参数Γ对能谱和量子Fisher信息Ft的影响.选取Γ=0.1,0.6,相应本征能谱的实部分别如图2(d)和图2(e)所示.可以看出,增大Γ对跳跃强度t0 附近的能谱影响比较明显.从图2(f)进一步看出,对于中间能态|ψmid〉,增大Γ除了移动能谱中4 个EP 点的位置,还会使得t0 处出现能隙闭合点.当Γ较大时(如Γ0.6),Ft会在t0 处出现峰值.相反地,如图2(g)所示,随着Γ的减小,能谱中心两侧的EP 相互靠拢;当Γ0 时合并于t0处,此时Ft在t0 附近指数增大.因此,该非互易模型中边界条件的变化可以通过能谱和量子Fisher 信息反映出来.

接下来考虑具有增益-耗散的非厄米SSH 模型[48,49],其动量空间哈密顿量为

令t′1,两能带为

能隙 ΔE随t和γ的变化如图3(a)所示.在ΔE ＞0和 ΔE0 区域,本征态能量分别为实数和复数,能隙闭合对应能带出现EP 点.考虑本征态|ψ-〉评估参数µk,主要结果如图3(b)所示.选取γ0.5,当t0.3和t1.7时,即图3(a)中的实能量区域,量子Fisher 信息Fk随参数k的变化较为平缓.当t1时,复能谱中k ≈0.84π,1.16π 两处有EP点,对应Fk在这两点附近呈现尖峰.而且Mk也反映了在具有EP 点的复能量区域,k的整体估计精度更高.

图3 基于具有增益-耗散的SSH 模型((a),(b))和非厄米量子Ising 链((c),(d))的单参数估计(a)能隙 Δ E 随t 和γ 的变化,有能隙区域能谱为实,无能隙区域能谱为复且存在EP 点;(b) γ 0.5和t{0.3,1,1.7} 时评估k 的量子Fisher 信息 Fk 随k 的变化;(c)能隙 ΔE 随λ 和h 的变化,能隙关闭处为复能量的铁磁态和顺磁态的相边界;(d)评估λ 时的 Mλ 随λ 的变化.图中 t′ 1 和J 1Fig.3.Single-parameter estimation based on the gain-and-loss SSH model((a),(b)) and the non-Hermtian quantum Ising chain((c),(d)):(a) Energy gap ΔE as functions of t and γ,and the gapped(gapless) region contains real(complex) eigen-spectrum(with exceptional points);(b) Fk as a function of k for estimating k with γ 0.5 and t{0.3,1,1.7} ;(c) energy gap ΔE as functions of λ and h,and the gapless line denotes the phase boundary between the ferromagnetic and paramagnetic states with complex energies;(d) Mλ as a function of λ for estimating λ.t′ 1 and J 1 are set.

本节最后考虑一维非厄米量子Ising 模型[50,51],其近邻格点自旋耦合强度为J,外加横场为复数场λ+ih(λ和h均为实数),模型哈密顿量为

其中准动量k ∈[0,π].令J1,本征能量为

能隙 ΔE随参数λ和h变化如图3(c)所示.考虑能量为E-的本征态,在参量空间λ-h中可分为铁磁态和顺磁态[50,51],其能量均为复数,但两者之间的转变伴随能隙的闭合.类似地,可利用此能量闭合特性提高参数估计的精度.如图3(d)所示,考虑参数µλ,选取h0.4,0.8,计算积分Mλ随λ的变化,可见Mλ分别在λ ≈0.92 和λ0.6的能隙闭合点附近形成尖峰.

3.2 两参数估计

对于两参数估计,首先考虑二维非厄米陈绝缘体模型[38,53,54],其动量空间哈密顿量为

其中准动量kx,ky ∈[0,2π],δ是非厄米强度.两能带记为E±(kx,ky),当能隙ΔE|E+(kx,ky)-E-(kx,ky)|＞0时,该非厄米模型的能带拓扑性质仍可用陈数C刻画[38,54]:

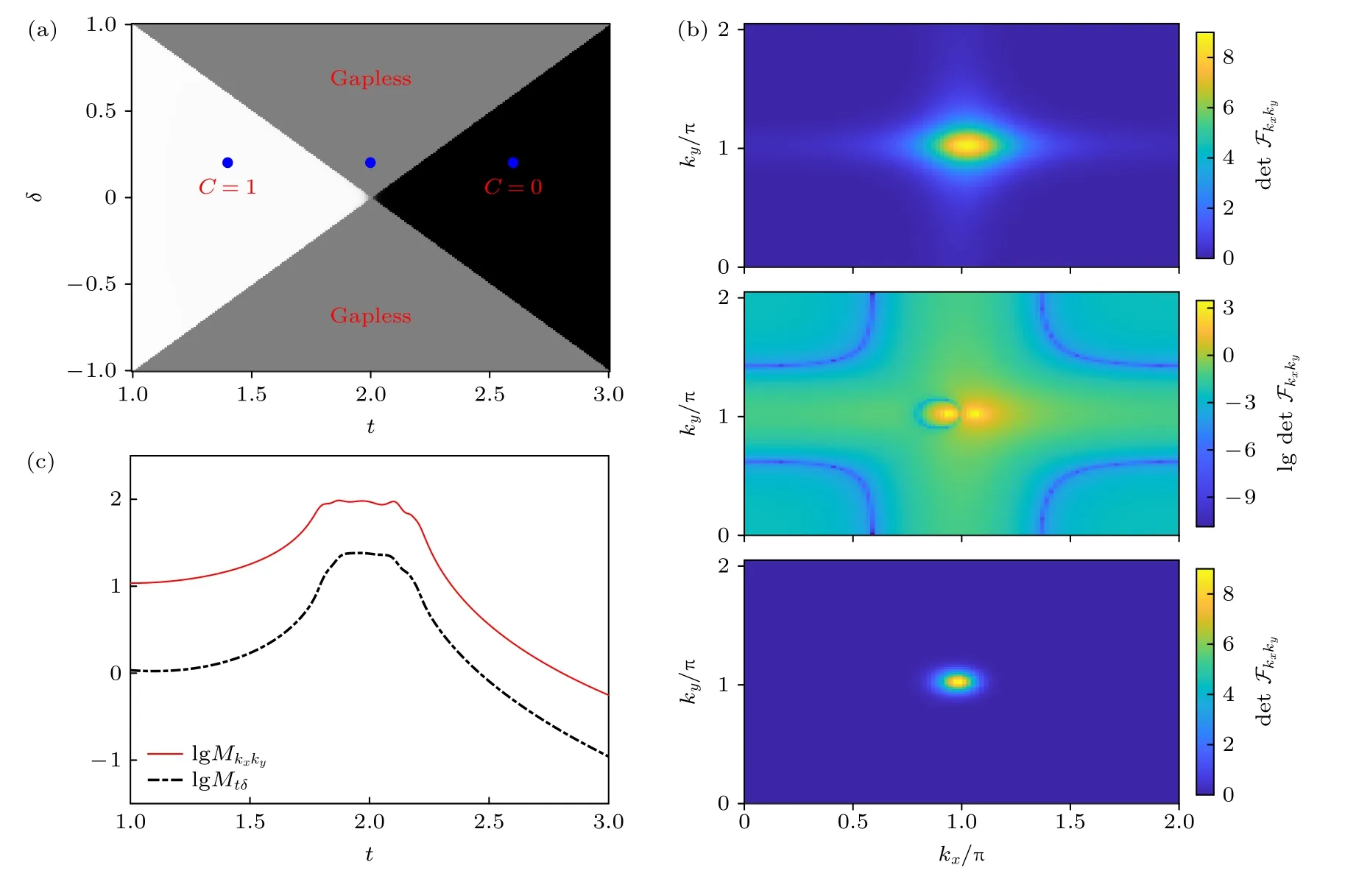
图4 基于非厄米陈绝缘体模型的两参数估计(a)拓扑相图,包括有能隙的拓扑和平庸区域,分别对应陈数 C 1和C 0,以及无能隙区域;(b) δ 0.2和t{1.4,2,2.6}(依次从上到下)时评估 {kx,ky} 的量 子Fisher 信息矩阵行列式 随kx,ky 的变化;(c) δ 0.2 时评估 {kx,ky}的 和评估 {t,δ} 的Mtδ 随t的变化.图(c)中 Mµν 和图(b)中间图做对数处理Fig.4.Two-parameter estimation based on the non-Hermtian Chern-insulator model:(a) Topological phase diagram with gapped topological(C 1),trivial(C 0),and gapless regions;(b) determinant of quantum Fisher information matrix as functions of kx and ky for estimating {kx,ky} with δ 0.2 and t{1.4,2,2.6}(from top to bottom);(c) the integration for estimating {kx,ky} and Mtδ for estimating {t,δ} as a function of t with δ 0.2.Mµν in panel(c) andin the middle of panels(b) are logarithmically plotted.

考虑两评估参数为µkx,νky,对应的量子Fisher 信息矩阵由方程(5)给出.图4(b)从上至下分别给出了t{1.4,2,2.6}和δ0.2时,行列式在动量空间中的分布.当t1.4 和t2.6时,分别对应有能隙的C1和C0 情况,det()在整个动量空间中变化较为平缓.当t2时,det() 在两个EP点kyπ 和kx ≈0.94π,1.06π附近呈指数增大.为表征整体评估精度,定义二维动量空间的积分

图4(c)给出了评估参数µkx,νky和µt,νδ两种情况下,Mµν随t的变化.可看出和Mtδ都在1.8 ≲t≲2.2 的无能隙区域取得更大值,表明此时两参数估计的整体精度更高.此外,相较于平庸区域,在拓扑区域的整体评估精度更高.

最后考虑具有等效增益-耗散项的非厄米二能级系统[26-28],其哈密顿量表达式为

其中仰角θ ∈[0,π] 和方位角φ ∈[0,2π] 给出归一化量子态在Bloch 球面上的位置,r代表沿z方向的偏置场强度,δ是非厄米强度.考虑实部能量较小的本征态,可定义陈数刻画系统的拓扑性质[10,11].如图5(a)所示,当r2+δ2＜1时C1,对应拓扑区域,而r2+δ2＞1 对应C0 的平庸区域.考虑评估参数µθ,νφ,从Mθϕ在r-δ参量平面中的变化可看出,相比平庸区域,拓扑区域的整体评估精度更高.由于拓扑转变伴随能隙关闭,因此Mθϕ的分布在r2+δ21附近出现尖峰.

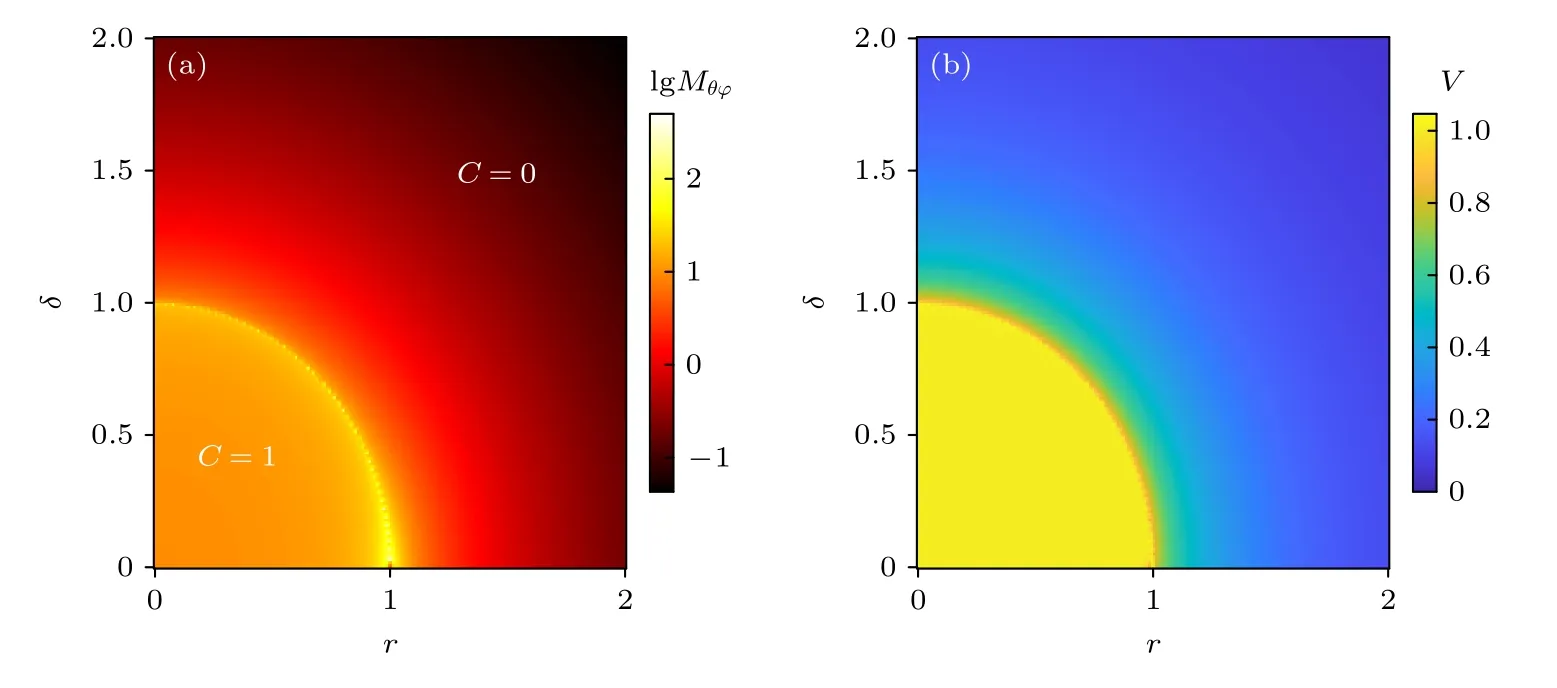
图5 基于非厄米二能级系统的两参数估计评估 {kx,ky}时,(a) 和(b)V 随r 和δ 的变化.图(a)中 做对数处理Fig.5.Two-parameter estimation based on the non-Hermitian two-level system.(a) and(b) V as functions of r and δ for estimating {kx,ky} . in panel(a) is logarithmically plotted.

此外|ψ-〉满足关系 det(Fθφ),从而给出此非厄米两能级系统中两参数估计的拓扑下界.为进一步讨论拓扑下界,可定义量子Fisher 信息矩阵行列式的积分:

结果如图5(b)所示,在拓扑区域中,贝里曲率Ωθφ在整个Bloch 球面上同号,可得VC1.在平庸区域,Ωθφ不满足同号条件,则 1＞V ＞C0.因此,量子Fisher 信息矩阵行列式可表征非厄米系统的拓扑转变.类似Mθϕ,V的结果也表明在拓扑区域中进行参数估计具有更高的精度,相应的量子Fisher 信息矩阵给出两参数估计误差的拓扑下界为陈数C.

4 结论与展望

本文基于量子估计理论,首先证明了对于非厄米哈密顿量归一化本征态,量子Fisher 信息(矩阵)的表达式以及单参数估计和两参数估计的QCRB 关系依然成立.在此基础上,计算了一维非互易、具有增益-耗散的SSH 模型和非厄米量子Ising 链中,量子Fisher 信息随动量或单个外场参数的变化.结果表明,基于这3 个非厄米模型的单参数估计,量子Fisher 信息在能隙闭合区域和EP 点附近呈现峰值,其动量空间积分也显著增大,因此可用于提高参数估计的精度.最后基于二维非厄米拓扑陈绝缘体模型和二能级系统进行两参数估计,同样地,量子Fisher 信息矩阵行列式及其动量空间积分在能隙闭合或EP 附近也明显增大.此外,量子Fisher 信息矩阵行列式在拓扑区域整体大于平庸区域,说明利用非厄米拓扑态进行参数估计的精度比平庸态更高,同时确定了两参数估计误差的拓扑下界.这些结果揭示了非厄米EP 点和拓扑特性在量子参数估计中的应用,有助于开展基于非厄米系统的量子精密测量研究.

目前已经有多个量子系统实验实现了非厄米有效哈密顿量,如单光子[24,25]、冷原子[26]、金刚石NV 色心[27]和超导量子比特[28]等.与此同时,最近已有实验报道了厄米系统量子Fisher 信息或量子度规的测量,如在金刚石NV 色心中测量单参数估计[12]和多参数估计[13-15]的量子Fisher 信息(矩阵),在核磁共振系统[18]中测量量子Fisher 信息,在超导量子比特系统[9-11]中测量量子度规等;甚至通过光子系统实验测量了非厄米有效哈密顿量中EP 点附近的量子度规[32].结合这些实验进展,本文基于非厄米系统的量子参数估计方案有望在实验中实现.最后需要指出的是,本文研究局限于非厄米哈密顿量本征态,如何基于非幺正演化动力学和开放系统中的混合态进行最优化参数估计需要进一步探索.另外,利用非厄米量子多体效应进行量子精密测量也是值得深入研究的课题.

附录A

考虑量子系统密度矩阵ρ|ψ〉〈ψ|,对于未知参数µ,ν的评估误差为 2×2 的协方差矩阵Σµν,相应的评估精度由 2×2 的量子Fisher 信息矩阵Fµν刻画.对于厄米系统中的量子态|ψ〉,量子Fisher 信息矩阵元为

其中{,}表示反对易关系,对称对数导数算符Lµ(ν)由∂µ(ν)ρ(Lµ(ν)ρ+ρLµ(ν))/2 定义.考虑定态情况中非厄米系统量子态|ψ〉,满足归一化条件〈ψ|ψ〉1以及相同的保留对称对数导数算符,其量子Fisher 信息矩阵元为

其中用到了关系 〈∂ψ|ψ〉-〈ψ|∂ψ〉.这里只利用非厄米系统特定本征态做参数评估,因此不受本征态的非正交性以及非幺正演化的影响.此时两参数估计的QCRB 仍满足Σµν≥1/Fµν,可以由矩阵的迹的柯西不等式得到:

而Fµν的非对角元与贝里曲率满足关系式