手性超材料惯容吸振器的扭转振动抑制研究1)

李 卉 魏国崇 姚红良 彭 禧

(东北大学机械工程与自动化学院,沈阳 110819)

引言

被动吸振是一种抑制结构振动的方法,在可靠性和经济性等方面通常优于主动振动控制[1].其中,动力吸振器(dynamic vibration absorber,DVA)通常作为被动减振方法[2-3],附加在主系统上以减轻力或运动的传递.以往的研究表明,DVA 以其高效、可靠和简便的特点被广泛应用于振动抑制方面[4-6].随着大型旋转设备在扭转振动抑制领域的发展,动力吸振器的结构也愈加复杂,因此追求其轻质化和简便化成为了学者研究的目标.

相较于传统DVA 结构,具有惯容结构的DVA(inerter dynamic vibration absorber,IDVA)采用一种机械机制来放大吸振器的“有效惯性”[7-9],如飞轮齿轮惯性[10-11]、滚珠丝杠惯性[12-13]和液压惯性[14-15]等.这种特点使得IDVA 在保持结构稳定性和紧凑性的同时实现了轻量化设计.Hu 等[16]结合不动点理论和代数解对IDVA 进行了分析和优化,有效提高结构体系的地震反应控制.Wang 等[17-18]对4 种基于惯容的新型负刚度DVA 进行了研究和优化,得到了闭环最优参数和改进的振动控制性能.Barredo等[19-21]对IDVA 进行了大量理论和实验研究,包括IDVA 优化,以及一种新型高性能非传统IDVA 的设计与优化.Sui 等[22]提出一种新的接地刚度惯容DVA,确定了惯容的有效范围,通过理论验证其具有良好的吸振能力.日益复杂的惯容设计限制了IDVA 结构在振动领域的广泛应用,一种简单高效的惯容机构应用于DVA 具有重要意义[23-24].

由于其独特的物理和机械特性,超材料的出现为衰减振动提供了一种新的方法[25-26].在各种类型的超材料中,自2017 年Frenzel 等[27]发现压缩-扭转耦合效应以来,手性超材料受到了广泛关注[28-29].其中,手性的概念已被引入到机械超材料的设计和振动抑制中[30].Jamil 等[31]提出了一种基于惯容的弹性超材料,并证明了其有效性.Zhao 等[32]开发了一种结合手性的晶格设计并应用于振动控制和隔离.手性超材料已被成功地应用于具有更低和更宽带隙的惯容结构,显示出其振动抑制的巨大潜力.此外,Lin 等[33]构建新型手性超材料并进行理论建模和有限元分析,研究表明这种手性超材料拥有较好的压扭-耦合效应.随着手性超材料的不断发展[26],其在吸振领域的应用也日益广泛.因此,结合手性材料对惯容结构进行改进和简化是研究的热点问题[34-35].

目前,通过附加动力吸振器的方法进行振动抑制已广泛用于消除机械系统的有害扭转振动中.然而,传统的吸振器质量较大,这限制了它在主系统扭转振动抑制中的应用.为了解决这一问题,本文提出一种手性超材料惯容吸振器(CIDVA),对其结构原理、抑振效果进行理论研究.通过手性超材料的压扭耦合特性,实现惯容机制的质量扩增,减少实际应用的转动惯量,抑制主系统的扭转振动,并通过仿真和试验验证CIDVA 的振动抑制能力.为DVA 实现轻量化设计和高效的振动抑制提供了新思路和方法.

1 基于手性超材料的惯容机制

1.1 手性超材料的压-扭特性

本文所采用的手性超材料结构如图1(a)所示,包括2 个振子盘和4 段螺杆.螺杆以振子盘的中心圆周分布,并以手性的方式排列.手性超材料的高度为h,初始夹角为 θ,则有h=lsinθ.

图1 手性超材料及CTC 效应Fig.1 Chiral metamaterials and CTC effect

手性超材料具有独特的压缩-扭转耦合效应,其几何关系如图1(b)所示.

设手性超材料上下振子盘分别为A1,B1,斜杆初始夹角为θ,假设某杆为PS,振子盘B1固定不动,对振子盘A1施加压力或者扭转力,扭转角为θc,扭转弧长PN2为

手性超材料单元胞在Z方向产生轴向位移.振子盘A1移动到A2,P点移动到N1点,则螺杆旋转角度也为PS与N1S夹角.螺杆长度l保持不变.并且可以得到它们之间的关系

设N1在振子盘A1的映射点为N2,则手性超材料沿Z轴轴向位移N1N2表示为

化简得 θc与N1N2的关系为

1.2 惯性放大

作为一种两端元件,惯容在各种机械系统中起着重要的作用.Smith 等[10]提出的惯容根据齿轮与飞轮之间的质量关系决定运动放大系数.而本文利用双手性超材料的压缩-扭转耦合效应来实现惯性放大.为了实现这种惯性放大作用,设计一种辅助机构限制手性超材料的局部运动.如图2(a)所示,移动约束限制双手性超材料沿z轴移动,而旋转约束限制双手性超材料绕z轴旋转.两者与手性超材料配合实现惯性放大,其内环固定在支撑轴上.两个移动约束分别与手性超材料CM1 和CM2 的上环和下环对齐.为防止摩擦,运动约束装置的支承梁不与振动环直接接触.该机构允许在输入端和输出端产生绕z轴方向的旋转运动,同时中介盘通过螺杆的空间变形实现沿z轴的轴向运动.

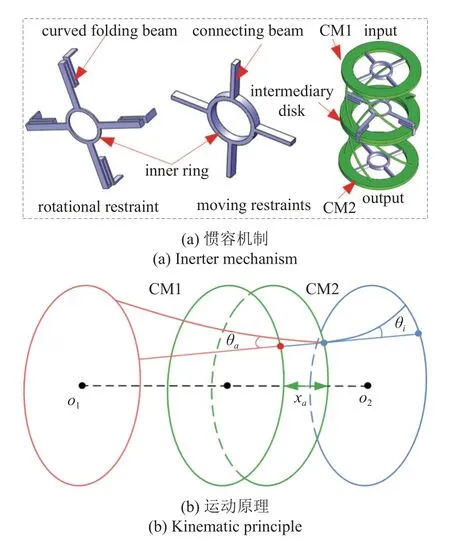
图2 惯容结构及运动原理Fig.2 Inerter structure and kinematic principle

手性超材料加上辅助机构,可以形成完整的惯容机制,实现惯性放大.运动原理如图2(b)所示,其中CM1,CM2 和中介盘分别用红、蓝、绿线表示.带箭头的绿线表示中介盘的运动方向.CM1 和CM2沿o1o2方向的轴向位移是共享的,对应绿环的移动距离.通过调整手性材料的参数,可以获得适当的惯性放大系数.

根据1.1 节推导的手性超材料CTC 效应的几何关系,可得吸振盘扭转角度θa和惯容盘θi分别与横向位移xa的关系为

式中,n1,r1和θc1分别为CM1 的螺旋度、振子盘半径和初始夹角;n2,r2和θc2分别为CM2 的螺旋度、振子盘半径和初始夹角.

简化得到θi和θa的关系

令b=r1n1tanθc2/(r2n2tanθc1)为惯性放大因子.

2 CIDVA 结构与建模

2.1 CIDVA 结构

基于手性超材料惯容机理的CIDVA 结构如图3 所示.它由DVA 盘、惯容盘、双手性超材料和辅助机构组成.双手性超材料用于连接DVA 盘和惯容盘.将旋转和移动约束附加到双手性材料上以提供方向限制.该结构具有体积小、重量轻、没有铰链间隙、高运动精度等优点,能够满足减振场景中对惯容的小尺寸、低重量和高可靠性需求.

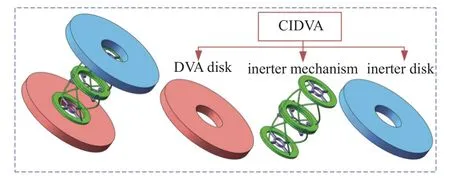
图3 CIDVA 结构示意图Fig.3 Structure of DCIDV

2.2 有限元仿真

使用ANSYS 有限元软件对CIDVA 进行仿真分析,验证CIDVA 惯容机制的放大系数.为了保证准确的比较和控制变量,设置DVA 盘和惯容盘的尺寸一致,提供相等的转动惯量.对初始角度递增的不同模型进行仿真分析,取CM1 初始夹角为10°,CM2 的初始夹角由10°递增至70°,其他参数为n1=n2=0.25 和r1=r2=18 mm.在理想情况和添加辅助机构两种情况下对CIDVA 运动进行分析.

理想情况下,在ANSYS 中设置圆柱支撑约束,DVA 盘和惯容仅允许切向运动,而中介盘仅允许轴向运动.仿真结果如图4(a)所示,CM2 的扭转量随着初始角度的增大而增大,而CM1 的扭转量变化不大,理论与仿真结果吻合较好.由此可知,通过调整CM2 的初始角度,将惯容的惯性放大系数调整到合适的范围是一种有效的方法.

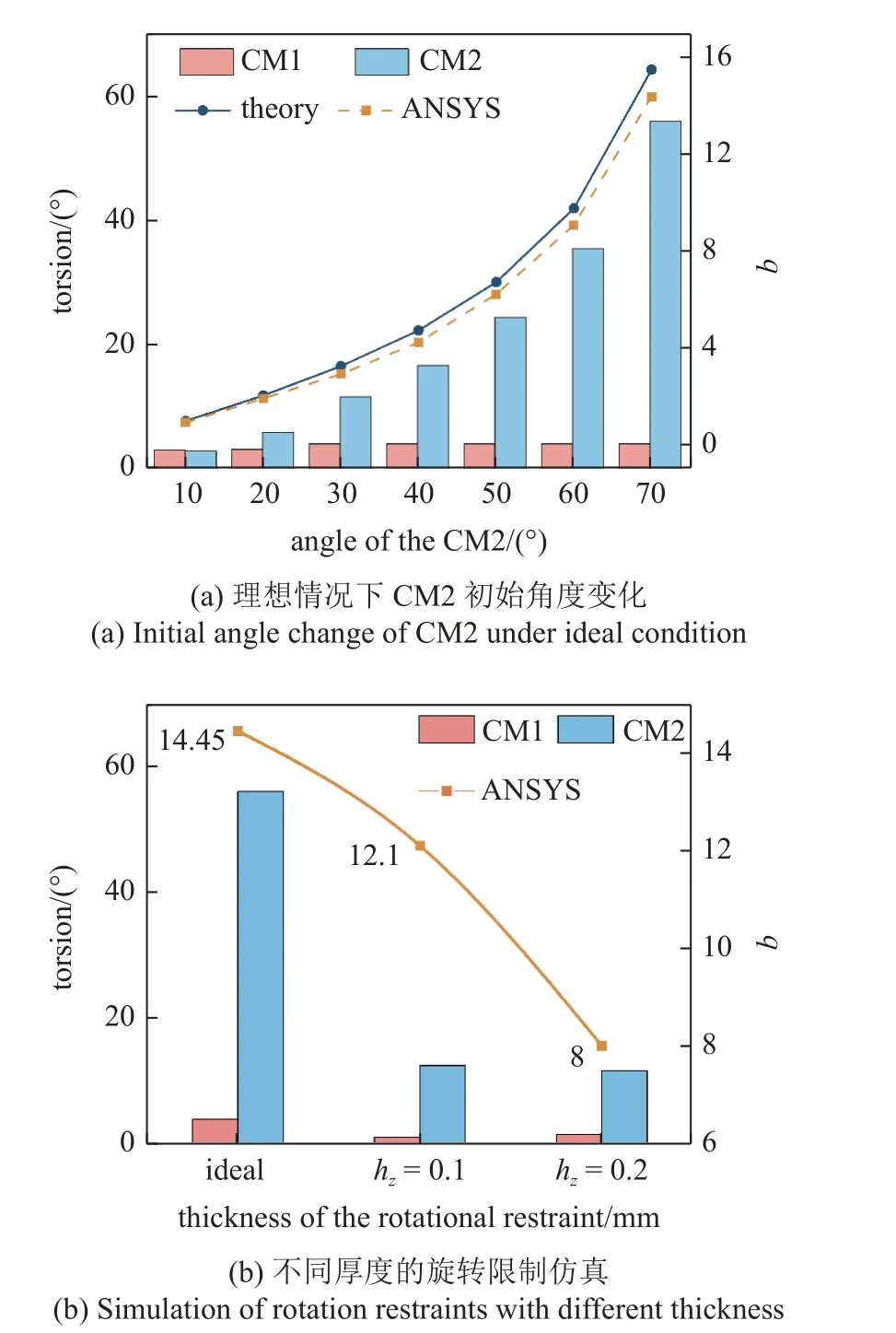
图4 CIDVA 仿真分析Fig.4 Simulation analysis of CIDVA

取CM2 初始角度为70°的模型,添加不同厚度的旋转限制进行仿真分析,结果如图4(b)所示.理想情况下该模型的惯性放大系数为14.45 倍,而添加辅助机构后,惯容盘的扭转减小.当hz=0.2 mm,惯性放大系数降低至8 倍,当hz=0.1 mm,惯性放大系数降低至12.1 倍.由此可知厚度较小的旋转限制对惯容机制的影响较小.但是,当hz=0.05 mm 时,旋转限制不能抑制CM1 的扭转,惯容机制失去放大效应.

2.3 主系统-CIDVA 动力学建模

主系统-CIDVA 结构如图5(a)所示,由主系统和CIDVA 两部分组成.主系统包括底座、主系统盘和支撑轴,其中主系统盘和支撑轴通过轴承连接.主系统盘在扭矩作用下转动,而支撑轴则固定不动.

图5 主系统-CIDVA 模型Fig.5 Primary system-CIDVA model

图5(b)为主系统-CIDVA 扭转振动动力学模型,根据牛顿第二定律,该耦合系统的运动方程为

式中,Jd和kd分别为主系统盘的等效转动惯量和扭转刚度;Ja,ca和ka分别为DVA 盘的等效转动惯量、扭转阻尼和扭转刚度.Ji为惯容盘的等效转动惯量;T=Tricos(ωt)为外激励扭矩,ω为转速.主系统和CIDVA 的扭转阻尼cd和ca分别表示为

式中,主系统的阻尼比 ξd=0.005,CIDVA 的阻尼比ξa=0.02.

将式(6)代入式(7),则有

为了评估CIDVA 的抑振性能,应建立附加锁定CIDVA 的动力学方程,CIDVA 的惯容盘仅有转动惯量对系统的动力学做贡献,主系统-锁定CIDVA的动力学方程为

3 仿真与讨论

3.1 参数设定

主系统盘的直径为120 mm,厚度为40 mm.DVA 盘和惯容盘的尺寸相同.主系统盘的材料是钢,DVA 采用3D 打印技术制作,材料为聚乳酸(polylactic acid,PLA).另外,为了保证柔性变形,旋转限制采用黄铜切割加工而成.基体材料参数见表1.主系统-CIDVA 仿真参数如下:Jd=7.8×10-3kg·m2;Ja=Ji=8.0×10-5kg·m2;kd=70.8 N·m/rad ;ka=9.1 N·m/rad ;手性超材料对应参数为仿真分析b=12.1 时模型,此时hz=0.1 mm.

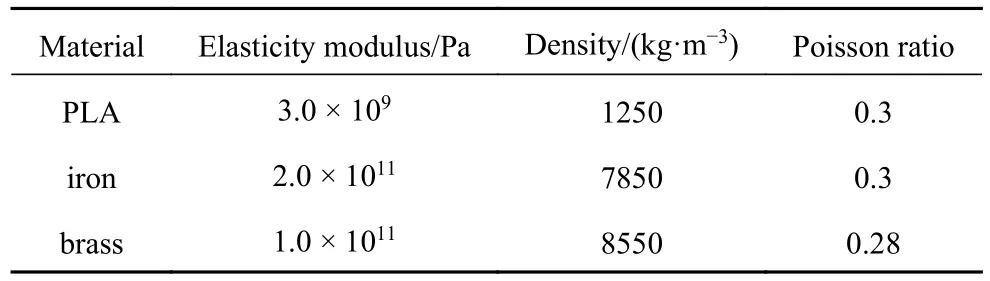
表1 基体材料参数Table 1 Material parameter

3.2 CIDVA 抑振性能分析

3.2.1 稳态响应

在稳态激励下,分析CIDVA 的扭转振动抑制特性.主系统-CIDVA 系统的初始条件设为

采用以上这组参数对主系统-CIDVA 进行稳态响应减振分析.令周期激励Tri=0.05 N·m.主系统-CIDVA 系统的稳态扭转振动响应如图6 所示,主系统一阶共振频率为15.1 Hz.对纵坐标位移幅值进行归一化处理后,附加锁定CIDVA 时,θd的共振峰值为1°.附加激活CIDVA 后,θd的最大幅值为0.26°.

The basic form of a transformer based matching network (TMN) is shown in Fig. 1, which consists of two parallel RLC tanks in the primary and secondary sides respectively, and a coupling coefficient k between them.

图6 主系统-CIDVA 的稳态扭转振动Fig.6 CIDVA-primary system steady-state torsional vibration

3.2.2 瞬态响应

本节研究了冲击激励下CIDVA 的扭转振动抑制性能.以初始角速度对系统进行初始激励,将初始角位移减小到较低幅值(小于初始角位移的10%)所需的时间用于分析CIDVA 的能量耗散速度.如图7(a)所示,主系统的初始角位移约为2.8°,降至0.28°需要约3 s 的时间.与锁定CIDVA 相比,激活CIDVA 提高了耗散速度.主系统在1.5 s 内衰减到0.28°左右,耗散速度比锁定CIDVA 快2 倍.相应的小波分析图如图7(b)所示.

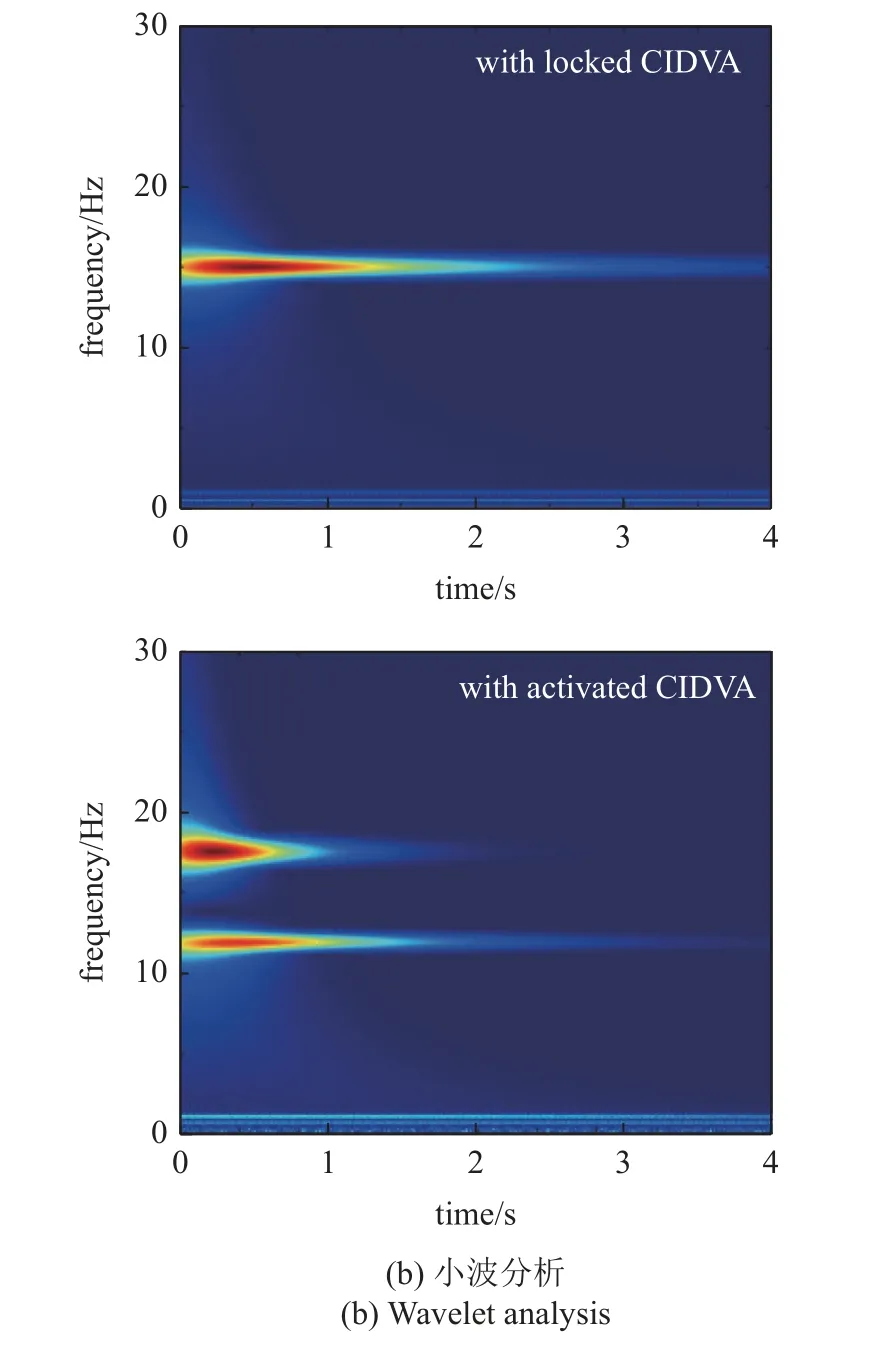
图7 CIDVA-主系统瞬态扭振Fig.7 CIDVA-primary system transient torsional vibration

3.3 惯容有效性

为了说明CIDVA 的惯容机制的优越性,将其与传统DVA 进行了比较.比较了两者在相同转动惯量下的抑振能力和相同抑振能力下所需的转动惯量.DVA 扭转振动抑制百分比的目标函数定义为

式中,θd_wo为附加锁定DVA 时的θd;θd_w为附加激活的DVA 的θd.

假设传统DVA 和CIDVA 的转动惯量为9.7×105kg·m2,并且假设两者的刚度和阻尼参数相等.而对位移幅值进行归一化处理后,稳态响应对比曲线如图8(a)所示.加入传统DVA 后,主系统的幅值基本没有减小.这表明在该参数设置下,没有惯容的辅助,传统DVA 对主系统没有抑制振动的作用.而CIDVA 展现出显著的扭转振动抑制能力.其次,比较了CIDVA 与传统DVA 在相同抑振效果下所需的转动惯量,验证了惯容机制具有节省必要质量的能力.对图8(b)和图8(c),传统DVA 的转动惯量需要比CIDVA 大13.74 倍,才能达到相近的约60%的抑振能力.传统DVA 最大扭振抑制百分比为71.8%,此时的转动惯量是CIDVA 的12.47 倍时,但抑振能力仍略低于CIDVA.

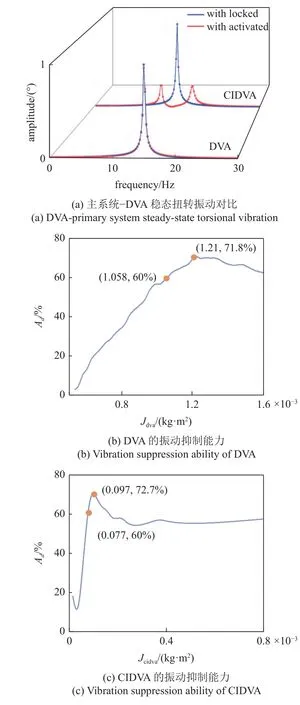
图8 CIDVA 与传统DVA 的对比分析Fig.8 Comparative analysis of CIDVA and traditional DVA

综上所述,在同等刚度、阻尼的参数条件下,无惯容结构的传统DVA 由于其转动惯量较小,对主系统盘的减振效果较差.而CIDVA 的惯容机制有效地增强了其抑制振动的能力,同时节省了10 倍以上的转动惯量,使其成为一种轻量化、简单的IDVA结构.

4 试验验证

搭建主系统-CIDVA 试验台,如图9 所示.阶梯轴与底座连接,底座固定在试验台上,起支撑作用.CIDVA 通过合适的扭转刚度弹簧和支座连接到主系统盘.DVA 盘和惯容盘通过轴承与阶梯轴连接,并随主系统盘的旋转而旋转.激振器与主系统盘连接,由信号发生器产生谐波信号经功率放大器传输.而主系统盘上的另一端安装加速度传感器,由LMS SCADAS 系统采集振动响应信号并研究.

图9 主系统-CIDVA 试验台Fig.9 Primary system-CIDVA experimentation apparatus

对主系统-CIDVA 进行扫频.扫描范围为1～80 Hz,扫描时间为1.5 Hz/s.未加CIDVA 的时域曲线如图10(a)所示,在20～30 s 内,红线处有较大的振动波动.附加CIDVA 后,主系统的振动响应明显衰减,如图10(b)中蓝色所示.验证了CIDVA 对主系统振动响应的抑制能力.

图10 试验测试结果Fig.10 Experimentation result

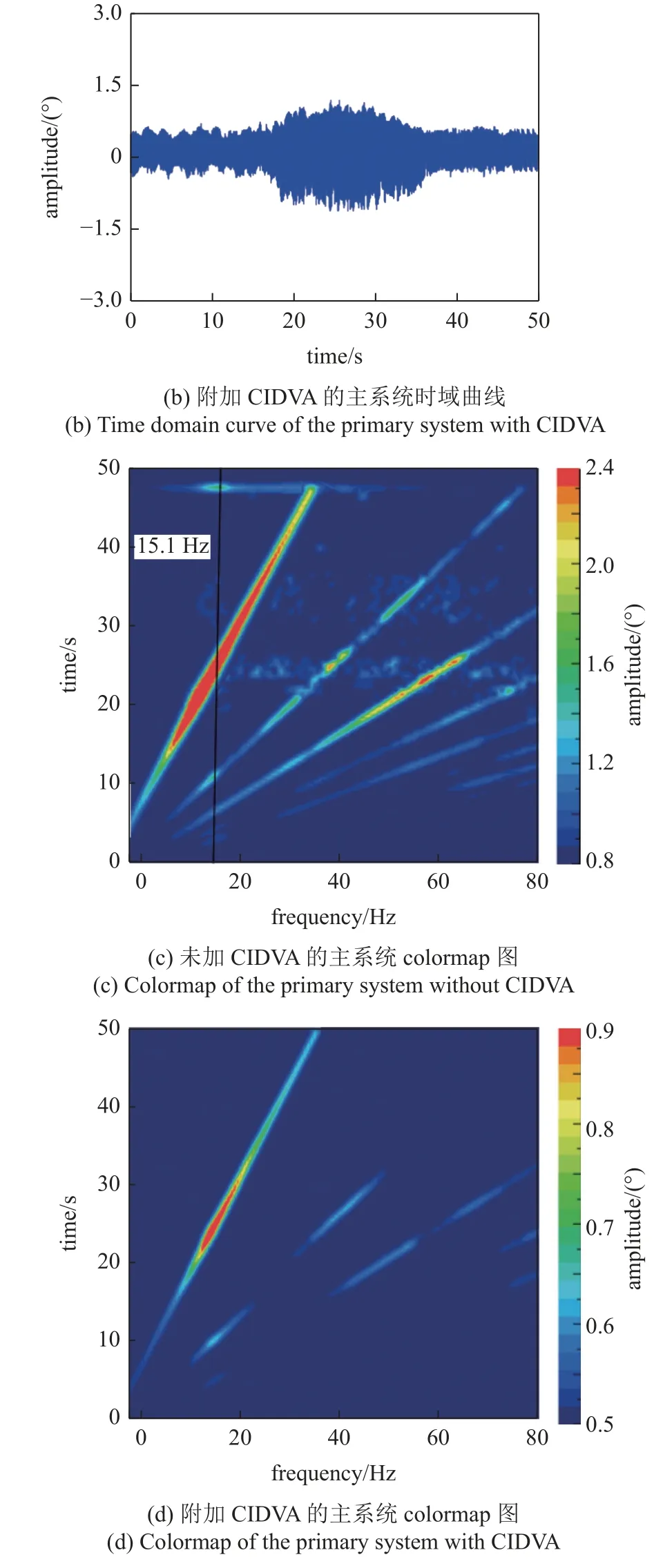
图10 试验测试结果 (续)Fig.10 Experimentation result (continued)

5 结论

本文提出了一种基于手性超材料惯容机制的CIDVA,并将其应用于主系统的扭转振动抑制,得出结论如下:

(1)CIDVA 通过手性超材料的压扭耦合效应实现惯容结构,进行质量扩增,相较于传统复杂的惯容结构更为简便、静质量小且减振效果更优;

(2)CIDVA 结构在瞬态激励和稳态激励下都展现出良好的振动抑制效果;

(3)对比无惯容结构的传统DVA,节省了相较自身10 倍以上的转动惯量.为DVA 实现轻量化设计和高效的振动抑制提供了新思路和方法.