渗流作用下粉土质砂潜蚀演化特征与预测模型

陈勇 闵泽鑫 夏振尧 隆海鹏

DOI： 10.11835/j.issn.2096-6717.2021.152

收稿日期：2021?06?07

基金项目：国家自然科学基金联合基金重点项目（U2040207）；中国地质调查局项目（0001212020CC60002）

作者简介：陈勇（1980- ），男，博士，教授，博士生导师，主要从事土-水耦合作用机制及边坡稳定性评价研究，E-mail： cyonger@126.com。

通信作者：夏振尧（通信作者），男，博士，教授，博士生导师，E-mail： xzy_yc@126.com。

Received： 2021?06?07

Foundation items： Key Project Supported by the Joint Funds of the National Natural Science Foundation of China （No. U2040207）; Project of China Geological Survey （No. 0001212020CC60002）

Author brief： CHEN Yong （1980- ）， PhD， professor， doctorial supervisor， main research interests： soil-water coupling mechanism and slope stability evaluation， E-mail： cyonger@126.com.

corresponding author：XIA Zhenyao （corresponding author）， PhD， professor， doctorial supervisor， E-mail： xzy_yc@126.com.

摘要：長期渗流作用下，土体发生内部潜蚀常会诱发结构变形甚至破坏。利用自主研发的渗流装置开展砂土潜蚀试验，研究渗流作用下不同初始孔隙比粉土质砂的颗粒流失过程及潜蚀演变特征，并阐明各影响因素的作用机制，建立颗粒流失量随水力梯度和时间增长的预测模型，继而基于颗粒级配试验和三相关系推演，揭示粒度分布与孔隙比的变化规律。结果表明：渗流作用易导致砂土内部细颗粒和砂粒流失并逐渐形成优势渗流通道，诱发砂土局部坍塌并在持续潜蚀后呈整体不均匀沉降变形，直至水压主要沿优势通道消散时，达到潜蚀稳定；初始孔隙比或密实度是影响土体潜蚀程度的主要内部因素，直接改变了颗粒移动的起动水力梯度、流失速率、累积总质量及土样沉降变形量，水力梯度增大会加快颗粒流失、通道形成和潜蚀稳定；建立的预测模型拟合度高，能较好地反映上述演化特征以及初始孔隙比和水力梯度对颗粒流失发展规律及稳定时间的影响；潜蚀对粉土质砂物理状态的影响主要表现在孔隙比总体增大而颗粒粒径的不均匀性降低。

关键词：砂土潜蚀；颗粒流失；水力梯度；孔隙比；预测模型

中图分类号：TU411.4     文献标志码：A     文章编号：2096-6717（2023）05-0018-08

Evolution characteristics and prediction model on suffusion of silty-sand subjected to seepage

CHEN Yong， MING Zexin， XIA Zhenyao， LONG Haipeng

（Key Laboratory of Geological Hazards on Three Gorges Reservoir Area， Ministry of Education， China Three Gorges University，Yichang 443002， Hubei， P. R. China）

Abstract： Soil suffusion induced by long-term seepage generally lead to deformation or damage of soil structure. The suffusion experiments of silty sand had been accomplished by the independently developed seepage instrument， to study the particle loss process and suffusion evolution characteristics of silty sand with different void ratios induced by seepage of different hydraulic gradients， and the influential mechanism of factors is understood on the sand suffusion， then a model is established to predict the increase of particle loss with seepage duration and hydraulic gradient. Furthermore， the development patterns are revealed of particles size distribution and void ratio during suffusion based on the particle grading test and three phases relationship. The results show that： firstly， fine and sandy particles are both washed away by the long-term seepage and some dominant seepage channels will form subsequently in the samples， and then the internal local collapse and the overall differential settlement will be induced by continuous suffusion， until the water pressure mainly dissipates along the dominant channel to achieve the suffusion stability. Secondly， the initial void ratio or compactness is the main internal factor affecting the degree of the seepage suffusion of the soil， which directly changes the hydraulic gradient threshold， loss rate， cumulative total mass of particle movement and settlement deformation of sandy samples. The increase of the hydraulic gradient will also accelerate the particles loss， channel formation and suffusion stability. Thirdly， the prediction model fits the experiment result well， which can reflect evolution characteristics above and the influence on particles loss process of initial void ratio as well as the hydraulic gradient. Finally， the void ratio of samples will increase and the uniformity of particle size will decrease during sand suffusion.

Keywords： sand suffusion； particles loss； hydraulic gradient； void ratio； prediction model

有关渗流引起土体潜蚀和结构破坏的研究已有一百多年，早期研究多集中在地貌学和地质学领域。随着大坝、堤防及深基坑等工程的修建，研究热点逐渐扩展到土力学理论，侧重于分析基于颗粒尺寸和级配的土体结构稳定条件，用于判定反滤层是否会出现内部侵蚀，并建立了土体自身结构稳定性评判标准[1-3]。近年来，有关渗流潜蚀的机理研究成为热点。Douglas等[4]基于22种土样试验结果，分析了各土样的潜蚀破坏模式；Ouyang等[5]侧重于研究细颗粒含量对土体潜蚀演化过程的影响；有研究通过模型试验发现，潜蚀时间与密实度呈正相关，但最终变形基本相同[6]；也有试验证明，水力梯度和水头增速会改变潜蚀破坏模式[7]；较多学者还关注了潜蚀发展过程与应力状态和应力路径的密切关系[8-10]。然而，上述研究仍停留在影响效果的定性描述上。有学者[11-13]重点关注细颗粒流失量与物理力学条件之间的定量关系，在对细顆粒流失过程的数学描述方面开展了探索性研究，基于级配良好砂的试验成果得出了细颗粒流失量与初始细颗粒含量、渗透坡降、渗流时间之间的经验公式，并建立了多个增量形式的密度变化方程，用于模拟渗流潜蚀下可动细颗粒的侵蚀和运移过程；也有研究者[14-17]采用不同数学模型和分析方法开展了土体的渗流潜蚀过程模拟。上述数学模型和数值模拟没有引入起动水力梯度，即假设水头差很小也会导致细颗粒全部流失，这与试验现象和实际工程存在明显差异。且由于潜蚀试验中细颗粒流失过程漫长、分布不均匀，很难达到完全稳定阶段，给模型的优化和应用增加了难度。

笔者提出“以梯度换时间”的思路，即通过增大水力梯度，加快渗流潜蚀直至稳定，以期确定细颗粒流失量与渗流时长及水力梯度的对应关系。具体方案是利用自主研发的渗流潜蚀试验装置，针对不同初始孔隙比的含粉粒砂土试样，设置3种较高的水力梯度，揭示土体潜蚀演变特征和发展规律，继而建立基于孔隙比、水力梯度和渗流时间的颗粒流失量预测模型，推求不同初始孔隙比土样在不同水力作用下达到潜蚀稳定的时长，并分析潜蚀对土样的孔隙比及粒度分布的作用规律。

1 试验装置及方案

1.1 试验装置及土样

自主研制的渗流潜蚀装置由控压供水系统、压力腔、细颗粒收集腔等部分组成。压力腔高150 mm、内径170 mm，外壁有刻度尺，上端连接不锈钢顶盖，顶盖上设两个孔分别连接进水管和排气孔，进水口连接压力表，腔内土样和顶盖之间设置透水石，压力腔底部设大孔径钢板筛作为承压板，土样与承压板之间放置1 mm的筛网；承压板下端连接细颗粒收集腔，收集腔出口连接一个不锈钢阀门，试验仪器模型如图1所示。

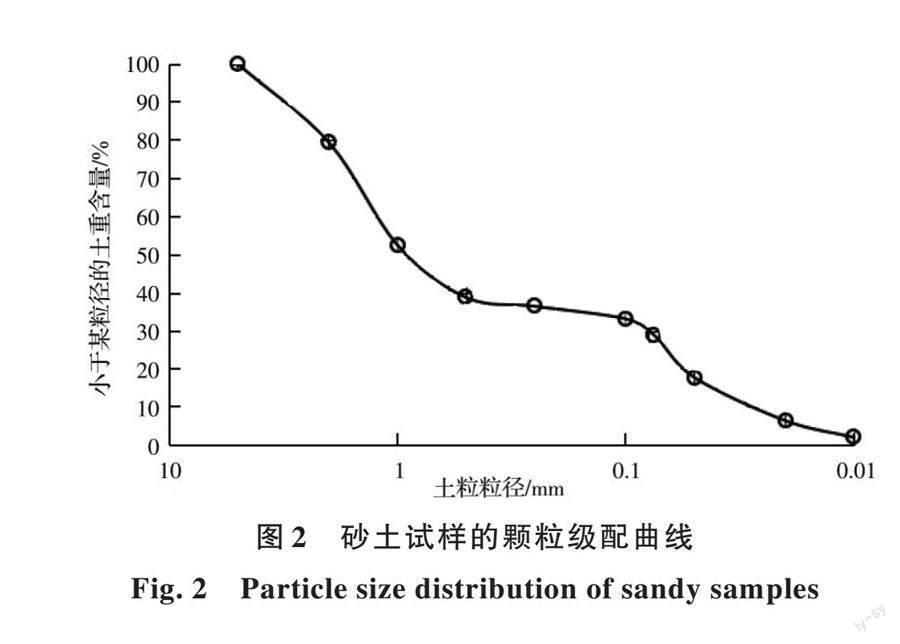
试验土样为取自某基坑的砂土，比重2.706，含水率16.4%，湿密度1.83 g/cm3，联合采用筛分法和密度计法确定土样的初始颗粒级配，如图2所示，不均匀系数Cu=52，曲率系数Cc=0.15，级配不良，细颗粒含量为28.9%，黏粒含量低于2%，按《土的工程分类标准》（GB/T 50145—2007）定为粉土质砂。

1.2 试验方案及步骤

根据研究目的及仪器特点，严格遵守土工试验规程。

1）试样的制备：根据现场砂样初始状态，考虑荷载作用后砂土压密，设置3种试样孔隙比，按照相同初始含水率配制试样，用塑料袋密封，于保湿缸内静置24 h。渗流试验共9个土样，初始参数及尺寸见表2，各试样中土颗粒质量基本相同。

2）装样及饱和：压力腔内壁涂抹一层防水胶，使其与颗粒黏结增强，以减弱侧壁绕渗。采用分层压样法将试样置于压力腔内，根据孔隙比的不同对试样高度进行调整，然后依次放置滤纸和透水石，用螺杆将顶盖、细颗粒收集腔与承压台紧固即完成装样。开启进水管阀门，打开排气孔，并关闭收集腔出水口阀门，将水流缓缓注入压力腔，使土样充满水，保持排气孔开启，静止24 h以确保土样趋于饱和后关闭排气孔。土样与顶盖之间留有30～60 mm高的充水空间，以便进口水压在该空间扩散后均匀作用于砂土表面。

3）渗流水力梯度设置：考虑到基坑底部砂土承受的水头较大，但从基坑底面溢出的路径较短，为增大渗流速率，缩短潜蚀稳定的时间，分析砂土潜蚀进程及其对物理力学性质的影响，将渗流的水力梯度设为10、15、20三个级别，可结合土样高度，调整输入水压力来实现，以确保水力梯度可稳定施加。

4）渗流试验及流失细颗粒称量：调节进水阀门，使渗透压力快速上升到目标压力值（目标水力梯度）并保持稳定，收集伴有细颗粒的浑水，每10 min更换一次收集器皿，待出水阀水流中见不到明显的细颗粒后，关闭进水阀门，停止渗流试验。各器皿中的浑水经静置、沉淀和烘干称重后，记录流失细颗粒的质量。

2 渗流潜蚀演化特征分析

2.1 渗流潜蚀现象

如图3、图4所示，在水流自上而下的裹挟作用下，细颗粒会在土体骨架内发生移动，且从试样底部开始；随着时间的推移，细颗粒向下运动的同时左右错动，土体内逐渐形成多个细微的渗流通道，孔隙变大，收集到的浑水浊度逐渐增大，此时，土样表面并未发现明显的下移现象；随着细颗粒持续流失，细微的渗流通道逐渐扩散连通，随后在渗透水流与土重挤压的共同作用下发生局部坍塌，进而出现较大的孔洞，伴随着明显的潜蚀破坏，通过标尺测量发现，土样表面也发生不均匀的沉降变形（孔隙比0.85的土样沉降量为5～25 mm）；随着水在优势通道的持续流动，收集水逐渐趋于清澈，细颗粒流失量逐渐减小，说明当前水力梯度已经无法使土样发生进一步的潜蚀，土体处于稳定状态。其主要原因是室内试验的潜蚀过程受到孔径1 mm筛网的限制，较大粒径的砂粒无法流失，颗粒骨架依然存在，与实际工程中通道完全贯通的现象略有不同。

2.2 细颗粒流失进程分析

按照试验方案，在预设水力梯度作用下，单位测量时间细颗粒流失质量随渗流时间的变化曲线如图5～图7所示（其中潜蚀后期单個器皿中颗粒质量小于0.2 g的不再计入），关键数据列于表3。由图表可以得到以下结论。

1）可将细颗粒流失过程分为骤增段、缓增段、平稳段3个阶段。骤增段约为渗透水压力加载最初的3 h，高水压力施加后，细颗粒快速起动，迅速流失，并随着细微优势通道的形成，细颗粒流失率快速增大并达到峰值，累积流失质量呈加速增加；在各优势通道逐渐连通，水流主要沿大的优势通道运动并诱发局部坍塌和堵塞后，细颗粒流失速率出现降低，此为缓增段；随着通道周围的细颗粒流失逐渐减少，单位时间的流失量趋于平缓，即为平稳段。试验中，水流达到完全清澈所耗时间很长，因此设置标准为单次测得颗粒流失质量小于0.2 g后潜蚀完全稳定。

2）随着施加的水力梯度增大，相同孔隙比的土样骤增段曲线变陡，细颗粒流失速率明显增大，达到最大流失率和最终潜蚀稳定的时间均缩短，由表3可知，水力梯度控制着土体渗流潜蚀的速率，且二者呈线性正相关关系。然而，对于相同孔隙比的土样，最终流失的细颗粒质量基本相同，其主要原因是渗透压力下的渗流潜蚀并非全域内均匀发生，土样细颗粒因流失不均匀而形成局部较大的优势通道，进而导致渗透水压沿通道快速消散，细颗粒流失总量不再继续明显增多。

3）相同水力梯度条件下，随着孔隙比的增大，细颗粒流失率峰值、最终累积流失量均增加，达到流失稳定的时间反而明显缩短，说明初始孔隙比是影响土体渗流潜蚀程度的主要内部因素，土体密实度直接改变了细颗粒移动的起动水力梯度、流失速率、累积总质量等。

3 潜蚀过程预测模型的构建

3.1 颗粒流失总质量预测

对流失颗粒的级配分析发现，受筛网直径影响，已流失颗粒的尺寸主要在0.5 mm以下。由表1和表3可知，潜蚀稳定后的累积流失颗粒总质量US并非等于所有0.5 mm以下可流动颗粒含量U0，而颗粒流失的比例主要与初始孔隙比e0相关。根据试验结果分析，通过数据拟合，建立预测关系为

U_S=U_0?exp（-b?〖e_0〗^c ） （1）

式中：b、c为参数，分别取0.93、0.44，试验结果Us-E与预测结果Us-P对比如表4所示。

3.2 颗粒流失演化过程预测

结合文献分析，只有在水力梯度大于起动值后，砂土才会出现颗粒流失，因此，其演化过程预测以确定起动水力梯度为前提。采用前述试验装置和相同的试样条件，结合进水阀和水压表逐级增大渗流水压力，每级压差约1 kPa（0.1 m水头）并持续10 min的渗流时间，观察收集的水中是否含有细颗粒，待收集水中细粒含量明显增大时，计算确定该土样的潜蚀起动水力梯度。结合施加的水压力值和试样高度，确定初始孔隙比为0.45、0.65、0.85条件下的起动水力梯度分别约为3.8、2.8、2.0，即孔隙比与起动水力梯度近似呈线性负相关关系。

以广泛应用的Sterpi D提出的预测公式为基础[11-12]，考虑到并非所有细颗粒均发生潜蚀移动，且存在启动水力梯度的影响，对预测公式进行修正，建立颗粒累积流失质量预测模型，如式（2）所示。

U_S^t=U_S?{├ 1-exp[-（├ t/t_0 ） ┤^m?n├ （i/i_0 ） ] ┤ } ┤ （2）

式中：U_S^t为t时刻的累积流失颗粒质量；t0为单位时间，1 h（60 min）；i0为起动水力梯度；m、n为参数，分别取1.51和0.015。拟合结果与试验值对比如图8～图10所示，其中：Ex为试验值；Pr为预测值。

3.3 预测结果对比与预测规律分析

由图8～图10可知，式（2）的预测模型能较好地反映累积流失颗粒随渗流时间的发展规律，预测结果与试验结果的误差如表5所示，其中（ΔUs）max代表最大误差，由某条件预测值与所有记录点试验值差值中的最大值确定，δ代表误差比，指前述最大值与最终累积流失颗粒总质量的比值。由表5可知，最大预测误差为28.9 g，最大误差比不到5%。

进一步，更改预测模型的输入条件，对模型的适用性及规律性进行验证。

首先，对3种不同孔隙比的土样设置不同的水力梯度，带入式（2）计算，预测结果表明：随着初始孔隙比的增大，达到潜蚀稳定的时间减小；且当初始孔隙比相同，即累积流失颗粒质量基本相同时，水力梯度越大，潜蚀稳定越快，如图11所示。

进一步，假设水力梯度20不变，针对不同孔隙比土样，根据前述的试验结果插值确定其起动水力梯度，并预测其颗粒流失规律及最终流失量。结果发现：对于相同质量和颗粒级配的土样，潜蚀进程均呈先骤增再减缓的趋势；且初始孔隙比越大，相同水力梯度下最终累积流失颗粒量越多，到达潜蚀稳定的时间越短，即颗粒越容易迁移，如图12所示。

4 潜蚀对砂土物理状态的影响

4.1 潜蚀对土样孔隙比的影响

潜蚀初期，颗粒流失造成土体孔隙增多，含水率增大，密度降低；当渗流孔洞增大、局部发生陡然沉降变形时，土体总体积瞬间减小、密度增大。可根据土中颗粒流失及体积变形的发展过程，确定孔隙比、密度、含水率等物理性质的演化过程。

e_t=（V_0 （1-ε_v^t ）-V_S^t）/（V_S^t ）=（M_S^0 （1+e_0 ）（1-ε_v^t ））/（M_S^t ）-1=

（（1+e_0 ） M_S^0 （1-ε_v^t ））/（M_S^0-U_S^t ）-1 （3）

当无体积变形，即ε_v^t=0时，式（3）简化为

e_t=（e_0 M_S^0+U_S^t）/（M_S^0-U_S^t ） （4）

式中：V_0、e_0、M_S^0分别为初始的总体积、孔隙比、土颗粒总质量；ε_v^t为对应时刻的体积应变；M_S^t和V_S^t分别为t时刻尚没有流失土颗粒的质量和体积；U_S^t为累积流失土颗粒的质量，即M_S^t=M_S^0-U_S^t。

将式（2）带入式（3）或式（4），结合测得的沉降变形特征即可预测土体的孔隙比随着施加水力梯度和渗流时间的演化规律，如图13所示。

由图13可知，渗流潜蚀导致土样颗粒流失、孔隙比增大，前期土样未见明显位移；但渗流通道扩散连通并出现局部坍塌时，土样总体积减小，孔隙比随之骤然降低；土样出现明显变形后，细颗粒流失量仍在缓增阶段，孔隙比也随之增大；亦即孔隙比的变化受土样沉降引起的体积减小量和细颗粒流失导致的孔隙增大量共同影响，但最终潜蚀稳定时孔隙比还是较初始值明显增大。需要说明的是，图13中的沉降量为土样表面不均匀沉降的均值，且由于沉降变形测量主要采用筒壁的刻度尺，精度有限，仅较好捕捉了明显坍塌时的骤降变形和最终变形量，区间微小沉降变形未能准确监测。

4.2 潜蚀对土样密度的影响

土体密度的演化规律可由式（5）预测。

ρ_t=（（1+w_t）G_S）/（1+e_t ） ρ_w=（G_S+s_r e_t）/（1+e_t ） ρ_w （5）

式中：G_S和ρ_w为土颗粒比重和水的密度；ρ_t、e_t、w_t分别为t时刻土体的密度、孔隙比和含水率；通常认为潜蚀多发生在饱和土中，饱和度s_r≡1。

将式（3）带入式（5），土体密度也可表示为

ρ_t=1/（1+ε_v^t ） [（（M_S^0-U_S^t）/（M_S^0 ）） ρ_0+（（U_S^t）/（M_S^0 ）-ε_v^t ） ρ_w ]     （6）

式中：ρ_0为土体的初始密度。当无体积变形，即ε_v^t=0时，土体密度可简化为

ρ_t=ρ_0-（U_S^t）/（M_S^0 ） （ρ_0-ρ_w ） （7）

将式（2）带入式（6）并结合沉降变形测量值，或将式（3）的e_t直接带入式（5）即可预测土体密度随着施加水力梯度和渗流时间的演化规律。

其他物性指标参照上述方法確定。

4.3 潜蚀对土样颗粒级配的影响

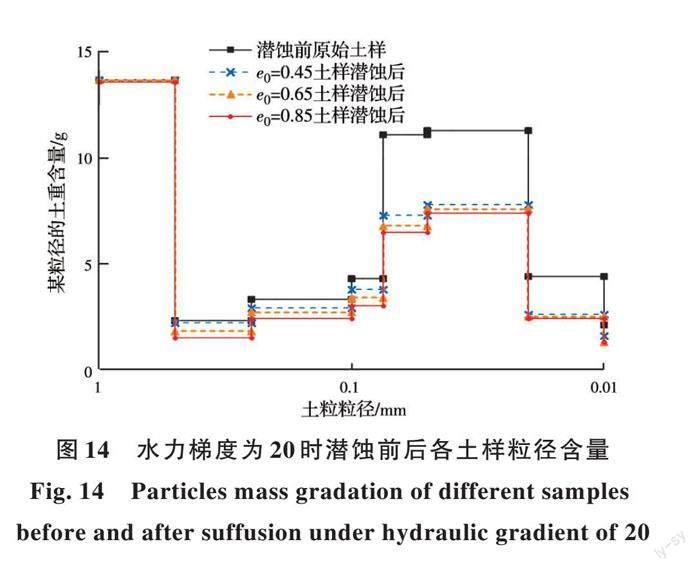
针对颗粒级配相同、初始孔隙比不同的土样，在水力梯度20时渗流潜蚀后，利用激光粒度分析仪对收集的流失土粒进行颗粒级配分析，初始颗粒含量减去流失颗粒含量即为渗流潜蚀后不同粒径的土重百分含量，如图14所示，纵坐标为某粒径的土重含量，粒径1 mm以上的土颗粒没有流失。

由图14可知：1）渗流造成土样潜蚀过程中，细颗粒和砂粒同步流失，且粒径0.075 mm以下的粉粒流失比例最高，约为40%，随着孔隙比的增大，粒径0.075～0.5 mm的砂粒流失量增大。由于受到筛网孔径为1 mm的限制，粒径0.5 mm以上砂粒基本没有出现流失;2）表1中粒径0.5 mm 以下颗粒含量为38.8%，由图13可知，潜蚀后3种孔隙比土样中粒径0.5 mm以下颗粒含量分别为28.2%、26.1%、24.5%，即随着孔隙比的增大，流失比例逐渐增加，分别达到27.3%～36.8%；3）尽管渗流潜蚀作用明显，但粉粒或砂粒并未全部流失，其主要原因是颗粒流失不均匀容易使土样局部形成优势渗流通道，造成局部渗透系数陡增，水压力未能长期均匀地作用于土样。

5 讨论

1）基于自主研发的渗流潜蚀仪器，观测了颗粒运移和土体沉降变化，并分析了孔隙比的演变规律，试验装置、试样尺寸虽与常见渗流试验规程中不一致，但并不影响试验结果。且传统管涌试验中水流多为由下至上，存在流失颗粒收集不完全的问题，本仪器将水流改为自上而下。

2）研究目的在于采用“水力梯度换侵蚀时间”的思路加快试验进程并建立潜蚀颗粒预测模型，因此，侧重于细颗粒流失质量的监控和分析，潜蚀过程中的流量和渗透系数变化数据也与细颗粒流失和孔隙比变化密切相关，相关成果将另文叙述。

3）结合数值模拟研究发现，1 mm筛网出口作为渗流临空面，水压力接近零；尽管土样内部的水力坡降并非均匀变化，但根据试样高度来控制水压力的变化能使整个土样的水力梯度平均值保持稳定。

4）由于试验土样不均匀系数大、细颗粒含量近30%，在水力梯度为1的水流自重作用下，水流溢出很慢，无细颗粒移动现象发生，因此，启动水力梯度始终大于1。

5）以往多数研究认为，土中细颗粒会随着潜蚀的发生而全部流失，事实上，还须考虑颗粒流失带来的渗流优势通道形成、土体结构变化、沉降变形、孔隙比变化等现象对土中细颗粒持续潜蚀移动的阻碍和影响。

6 结论

为进一步探索潜蚀发展进程和最终颗粒流失量，采用自主研发的渗流潜蚀仪器，选用不同孔隙比土样并设置不同的水力梯度以加速潜蚀稳定的速度，模拟了渗流水压对粉土质砂的潜蚀作用，描述了颗粒流失演化特征并分析了其主要影响因素，继而建立了预测模型，最后分析了潜蚀对砂土孔隙比、密度、颗粒级配的影响规律，主要结论如下：

1）受到试验装置中筛网孔径的影响，高渗透力作用下大颗粒未能持续移动，潜蚀现象会逐渐趋于稳定。试验现象有力证实了在潜蚀发生初期设置防渗土工布对周边土体持续潜蚀及大面积管涌破坏能起到重要抑制作用。

2）初始孔隙比（密实度）是影响砂土渗流潜蚀程度的主要内部因素，直接改变了细颗粒移动的起动水力梯度、流失速率、累积总质量等指标。而高水力梯度的施加主要加快了砂土潜蚀速率和优势通道的形成，缩短了潜蚀稳定时间。

3）建立的预测模型反映了潜蚀稳定时累积流失颗粒总质量由“可流动颗粒含量”及“初始孔隙比”两个因素决定，也反映了流失颗粒总质量主要受水力梯度和渗流时间控制，采用“水力梯度换侵蚀时间”的思路是可行的。

4）砂土被潜蚀后孔隙比总体呈增大趋势，影响其变化特征的因素包括颗粒流失引起的孔隙增多和沉降变形导致的总体积减小；孔隙比增大会加大潜蚀程度，而潜蚀的发展也定会造成孔隙比进一步增大，二者是耦合发展的。

5）渗流作用使砂土中细颗粒和砂粒同步流失，潜蚀稳定时，0.075 mm以下细粒流失比例达到40%，土样不均匀性明显减小，且砂粒流失量随着初始孔隙比的增大而增加。

虽然通过一系列室内试验和理论分析描述了渗流作用下粉土质砂潜蚀的演化过程、预测模型及潜蚀对物理状态的影响规律，但仍有较多问题急需进一步研究和解决，如试验对象类型有待扩展，颗粒级配的作用机理有待揭示，孔隙比与潜蚀的耦合促进机制有待阐明，沉降变形测量的精度和实时采集有待提高，筛网孔径的影响也有待深入分析。

参考文献

[1]  WAN C F， FELL R. Assessing the potential of internal instability and suffusion in embankment dams and their foundations [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2008， 134（3）： 401-407.

[2]  CHANG D S， ZHANG L M. Extended internal stability criteria for soils under seepage [J]. Soils and Foundations， 2013， 53（4）： 569-583.

[3]  INDRARATNA B， ISRAR J， RUJIKIATKAMJORN C. Geometrical method for evaluating the internal instability of granular filters based on constriction size distribution [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2015， 141（10）： 04015045.

[4]  DOUGLAS K J， FELL R， PEIRSON W L， et al. Experimental investigation of global backward erosion and suffusion of soils in embankment dams [J]. Canadian Geotechnical Journal， 2019， 56（6）： 789-807.

[5]  OUYANG M， TAKAHASHI A. Influence of initial fines content on fabric of soils subjected to internal erosion [J]. Canadian Geotechnical Journal， 2016， 53（2）： 299-313.

[6]  SHARIF Y A， ELKHOLY M， HANIF CHAUDHRY M， et al. Experimental study on the piping erosion process in earthen embankments [J]. Journal of Hydraulic Engineering， 2015， 141（7）： 04015012.

[7]  MING P， LU J， CAI X， et al. Experimental study on internal erosion and seepage in the foundation of a dike under variable water head [J]. European Journal of Environmental and Civil Engineering， 2021： 1-16（11）：5073-5087.

[8]  CHANG D S， ZHANG L M. Critical hydraulic gradients of internal erosion under complex stress states [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2013， 139（9）： 1454-1467.

[9]  蔣中明， 王为， 冯树荣， 等. 应力状态下含黏粗粒土渗透变形特性试验研究[J]. 岩土工程学报， 2014， 36（1）： 98-104.

JIANG Z M， WANG W， FENG S R， et al. Experimental study on influence of stress state on seepage failure characteristics of coarse grained soil with cohesive particles [J]. Chinese Journal of Geotechnical Engineering， 2014， 36（1）： 98-104. （in Chinese）

[10]  WANG G， HORIKOSHI K， TAKAHASHI A. Effects of internal erosion on parameters of subloading cam-clay model [J]. Geotechnical and Geological Engineering， 2020， 38（2）： 1323-1335.

[11]  STERPI D. Effects of the erosion and transport of fine particles due to seepage flow [J]. International Journal of Geomechanics， 2003， 3（1）： 111-122.

[12]  CIVIDINI A， BONOMI S， VIGNATI G C， et al. Seepage-induced erosion in granular soil and consequent settlements [J]. International Journal of Geomechanics， 2009， 9（4）： 187-194.

[13]  YANG J， YIN Z Y， LAOUAFA F， et al. Hydromechanical modeling of granular soils considering internal erosion [J]. Canadian Geotechnical Journal， 2020， 57（2）： 157-172.

[14]  沈辉， 罗先启， 毕金锋. 土石混合体渗透侵蚀特性数值模拟研究[J]. 岩土力学， 2017， 38（5）： 1497-1502， 1509.

SHEN H， LUO X Q， BI J F. Numerical simulation of internal erosion characteristics of block in matrix soil aggregate [J]. Rock and Soil Mechanics， 2017， 38（5）： 1497-1502， 1509. （in Chinese）

[15]  ZHANG L L， WU F， ZHANG H， et al. Influences of internal erosion on infiltration and slope stability [J]. Bulletin of Engineering Geology and the Environment， 2019， 78（3）： 1815-1827.

[16]  雷小芹， 刘恩龙， 何思明， 等. 非饱和堆积土边坡降雨-渗流潜蚀耦合过程模拟[J]. 工程科学与技术， 2021， 53（2）： 28-37.

LEI X Q， LIU E L， HE S M， et al. Modelling of coupled process of rainfall infiltration and internal erosion within unsaturated deposited soil slopes [J]. Advanced Engineering Sciences， 2021， 53（2）： 28-37. （in Chinese）

[17]  王越林， 陸烨. 城市地区管道渗漏引发地面塌陷成灾机理的CFD-DEM联合计算模拟分析[J]. 土木与环境工程学报（中英文）， 2021， 43（2）： 60-67.

WANG Y L， LU Y. CFD-DEM simulation of disaster mechanism of pavement collapse caused by pipeline leakage in urban areas [J]. Journal of Civil and Environmental Engineering， 2021， 43（2）： 60-67. （in Chinese）

（编辑  胡玲）