蜗杆砂轮磨削齿面纹理主动调控方法研究＊

田晓青 武众磊 唐建平 游通飞 韩 江 夏 链

（①合肥工业大学机械工程学院，安徽 合肥 230009；安徽省智能数控技术及装备工程实验室（合肥工业大学），安徽 合肥 230009）

齿轮是人类社会生产生活过程中重要的基础零件，随着工业的不断发展，对齿轮的要求越来越高，齿轮传动朝着更加精密、更加低噪和更加高效的方向发展。在新能源汽车迅速发展的今天，齿轮噪声严重影响了传动效率和驾驶体验，低噪声意味着更强的竞争力。Hansen B 等[1]研究表明，几何精度高的齿轮依然存在高噪声的情况。1992 年，Mark W D[2]的研究结果表明齿轮齿面的波动误差会影响斜齿轮的传动误差，从而增大了齿轮噪声的强度。Amini N 等[3-4]发现在齿轮啮合的轨迹上存在着规则且有周期性的齿面细微结构，容易生成聚集在齿轮啮合频率及其谐频带上的噪声，由实验证明齿轮噪声与齿面细微结构有关。已有的研究表明齿轮噪声的激励源主要来自齿轮冲击、传动误差和摩擦等[5]。齿轮的表面形貌，包括粗糙度、波纹度和纹理等表面微结构决定齿轮噪声激励源也已成为普遍共识。然而，倾斜不规则纹理的生成方法在行业中是高度机密，还未公开。因此，研究齿面纹理的主动控制有重要意义。

常见的改变齿面纹理的方法有改变加工的某些工艺参数和增加刀具运动轴附加量。Jolivet S 等[6]通过试验证明了齿面波长与实际的加工方式有关，与波长单一的齿面形貌相比，具有混合波长的齿面形貌可以降低齿面缺陷的影响，倾斜且不规则的齿面纹理更有利于齿轮的啮合。Schenk T 等[7]通过设计一种高性能珩磨轮，研究了切削速度和轴交角的关系，获得珩削齿面纹理分布与齿轮中心距和轴交角的关系。杨树峰等[8]通过滚磨光整加工工艺显著降低弧齿锥齿轮表面粗糙度，降低了锥轴齿面粗糙度和锥盘粗糙度值，显著提高了齿面纹理的一致性，便于弧齿锥齿轮的振动和噪声特性的研究。李国龙等[9]通过研究磨齿的磨削特性对齿面细微结构的作用效果，对加工过程中的冲程速度施加正弦函数，加工出分布不规则的磨齿齿面纹理。韩江等[10]通过内啮合强力珩齿工艺，研究了中心距和轴交角对珩齿齿面纹理的影响，实现了珩齿加工工件齿面纹理的主动控制。瑞士的制造商Reishauer[11]在磨齿加工中采用低噪声偏移技术，对机床加工轴附加运动，生成了倾斜且不规则的纹理，具有较好的降噪效果。

目前国内对磨齿纹理的研究比较少，磨齿齿面纹理的调整还未找到有效的控制方法。参考上述研究，本文进一步研究了磨削过程中机床X、Y和Z轴的附加加工运动，以实现对齿面纹理的调整，提出一种基于电子齿轮箱的通过对X、Y和Z轴附加运动进而实现磨削齿面纹理主动调控的方法。将仿真结果与国外尚未披露的方法进行比较，证明了本研究的可行性。

1 蜗杆砂轮磨齿和齿面纹理角度建模

齿轮加工机床采用的是重庆机床集团的YW7232CNC 磨齿机，主要轴示意图如图1 所示。砂轮和齿轮的基本参数见表1。

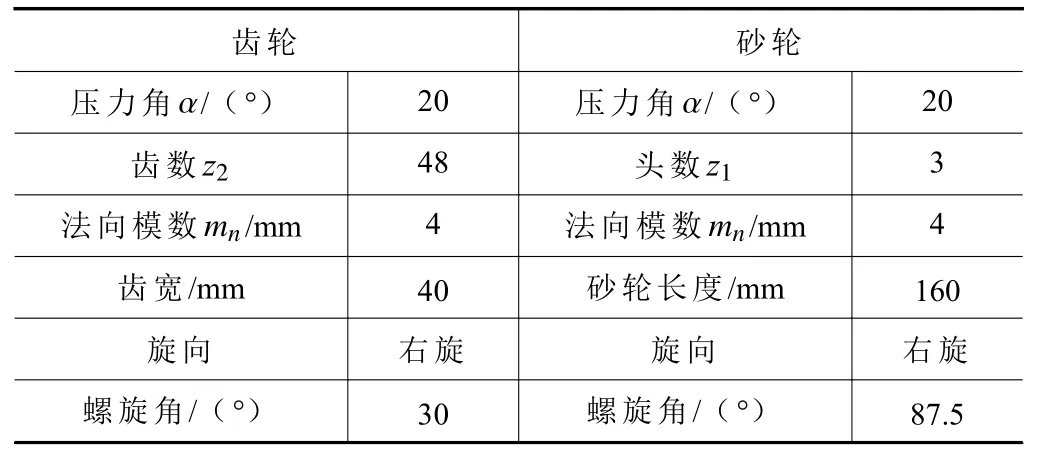
表1 基本参数

图1 磨齿机主要轴示意图

1.1 齿轮和砂轮模型的建立

图2 所示为齿轮端截面廓形，以齿轮圆心为坐标原点o建立坐标系xoy，竖直向上为x轴正向，水平向右为y轴正向，rb为基圆半径，σ0为oe与x轴正向夹角，e点为渐开线起点，取∠eoa0=(µ>0)为参数，根据渐开线的性质可知：Ma0=rbµ。

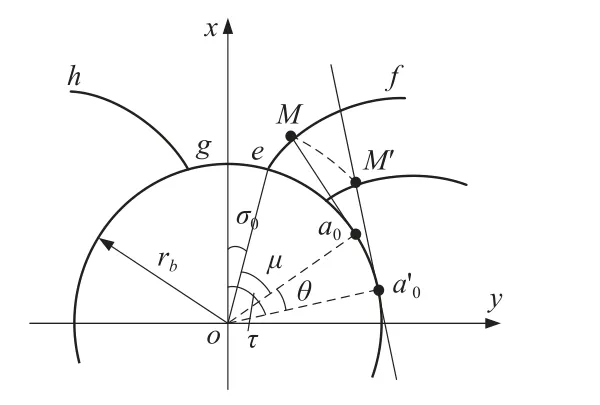
图2 齿轮端截面廓形

以右侧齿面为例，渐开线ef的参数方程为

渐开线ef绕着z轴螺旋运动，旋转得到渐开线螺旋齿面[12]，公式如下：

式中：θ为渐开线绕z轴旋转的角度，βb为基圆螺旋角。

对 µ 和 θ求偏导后外积可得到曲面的法向量ng(µ,θ)表达式为

同理可得左齿面的参数方程以及曲面法向量。

同样地，可以表示蜗杆砂轮的坐标rw(ξ,τ)和法向量nw(ξ,τ)：

式中：ξ和τ为蜗杆砂轮的两个参数；基圆半径rw为150 mm；p是螺旋参数，为6.730 mm；∆Zw是蜗杆砂轮的齿槽角参数，为-22.3 mm；βw为砂轮螺旋角，为87.5°。

1.2 蜗杆砂轮磨齿空间坐标系的建立

式中：v01为砂轮轴向进给速率；v02为砂轮切向进给轴进给速率；t为加工时间。

图3 所示为齿轮和砂轮的空间啮合坐标系，坐标系S(O-X,Y,Z)与S p(Op-Xp,Yp,Zp)是空间固定坐标系，坐标系S1(O1-X1,Y1,Z1)与S2(O2-X2,Y2,Z2)分别与砂轮、齿轮固联，Z1轴、Z2轴分别与砂轮、齿轮回转轴线重合，a是中心距，Σ为轴交角，φA、φB、φC、LX、LY、LZ分别表示A轴、B轴、C轴、X轴、Y轴、Z轴的运动量。

图3 砂轮、齿轮啮合坐标系

刀具坐标系到工件坐标系的坐标变换矩阵M21：

式中：

M2p、Mp0、M01分别是坐标系S p(Op-Xp,Yp,Zp)到坐标系S2(O2-X2,Y2,Z2)、坐标系S(O-X,Y,Z)到坐标系S p(Op-Xp,Yp,Zp)、坐标系S1(O1-X1,Y1,Z1)到坐标系S(O-X,Y,Z)的变换矩阵。

坐标系S(O-X,Y,Z)坐标与坐标系S1(O1-X1,Y1,Z1)坐标的转换关系为

设空间中有一点M（图3），则有：

M点随砂轮运动的速度v1和随齿轮运动的速度v2为

式中：ω1为蜗杆砂轮的角速度；ω2为工件齿轮的角速度；两者均为矢量，其标量单位为rad/s。

在S(O-X,Y,Z)坐标系下：

在电子齿轮箱[13]中：

式中：z1、z2分别为砂轮头数和齿数；β、λ分别为齿轮螺旋角和刀具安装角，单位为度；齿轮右旋时螺旋角为正，左旋时螺旋角为负；mn为法面模数，单位为mm；kB、kZ、kY为系数常量；砂轮右旋时kB=1，砂轮左旋时kB=-1。

当v02<0、β>0时，kZ=1；当v02<0、β<0时，kZ=-1；当v02>0、β>0时，kZ=-1；当v02>0、β<0时，kZ=1；当v01>0时，kY=1；当v01<0时，kY=-1。

砂轮和齿轮在M点的相对运动速度v12为

将式（4）、式（5）、式（8）～式（15）代入式（18）可得

1.3 齿面磨削纹理产生原理及纹理角度的表示

如图4 所示，蜗杆砂轮相当于一个螺旋角很大的圆柱斜齿轮，在空间中与齿轮啮合[14]。磨削过程中，刀具经过滑擦、耕犁和切削3 个过程切除材料。与此同时，会在齿面上形成一条条接触迹线，每条接触迹线上产生一个个磨削印痕（图5）。磨削路径的方向决定了磨削印痕的方向。理想状况下，每个磨削印痕的形状相同，砂轮与工件的磨削速比vw/vg决定了磨粒的磨削运动[15]。齿面的磨削纹理由一个个磨削印痕相连而成，所以可以通过控制每个磨削印痕的导向，即控制每个磨削印痕与齿向的夹角来达到宏观上控制齿面磨削纹理的目的。

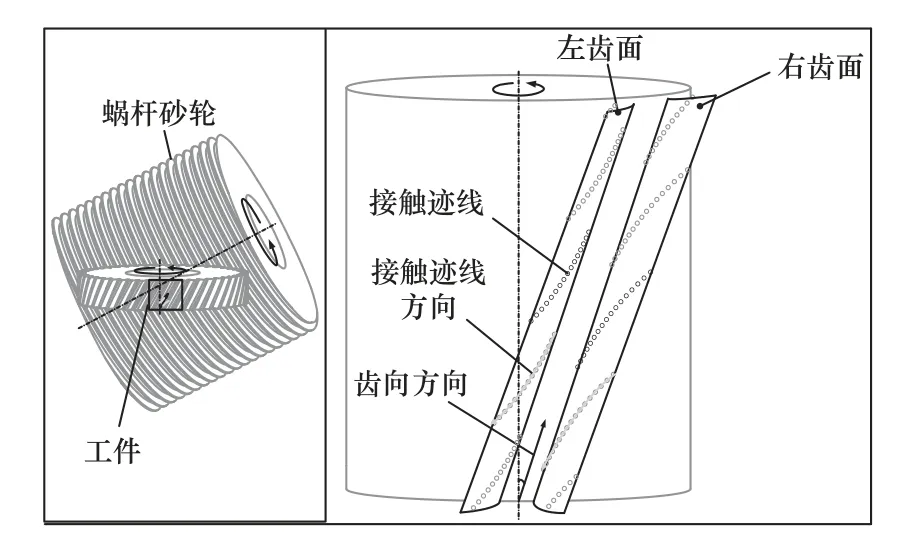
图4 蜗杆砂轮与齿面示意图

图5 齿面磨削印痕示意图

包络齿面坐标和法向量在S2(O2-X2,Y2,Z2)坐标系中表示为

式中：rw′(ξ,τ,φB,LY,LZ)为蜗杆砂轮在S2(O2-X2,Y2,Z2)下的包络齿面坐标；nw′(ξ,τ,φB,LY,LZ)为蜗杆砂轮在S2(O2-X2,Y2,Z2)下的包络齿面法向矢量；LCB为MCB左上3 ×3 子矩阵。

蜗杆砂轮产生包络齿轮的包络齿面的必要条件为

如图6 所示，蜗杆砂轮产生的包络齿轮的包络齿面与目标齿面坐标相同，向量方向相反。目标齿面法向量ng(ξ,τ,φB,LY,LZ)为

图6 蜗杆砂轮表面与目标齿面示意图

S1(O1-X1,Y1,Z1)坐标系中点M1的坐标为rw(ξ,τ)，过M1的蜗杆砂轮“齿向”切线与端截面渐开线的交点记为，其坐标为rw(ξ,τ)τ=0，蜗杆砂轮“齿向”切线用表示。

目标齿面齿向切向量nLEAD可表示为

齿面某一点M2的磨削印痕与齿向的夹角 α由nLEAD与v12的夹角表示

2 附加运动函数求解

常规蜗杆砂轮磨削加工后，齿面会形成规则的、α几乎为0 的齿面纹理，这种纹理容易产生较大的啮合噪声。为了改善齿面纹理，生成不规则的有一定倾斜角的齿面纹理，则在X轴、Y轴和Z轴上分别施加多项式，生成齿面纹理角度与多项式系数的函数关系：

接下来，采用敏感度矩阵（SM）结合Levenberg-Marquardt（LM）算法确定运动轴（X轴、Y轴、Z轴）附加运动函数的各个系数。

构建敏感度矩阵Ms如下：

式中：N为单侧齿面网格点数量，等式右边矩阵为敏感度矩阵，即

式中：δ为表示变量变化量的符号。

多项式系数的变化量可以使用最小二乘法求解：

采用奇异值分解求Ms的伪逆

式中：U为2N×2N阶酉矩阵；W为对角矩阵；VT为12×12阶酉矩阵。

式中：矩阵W+为W的伪逆，将W的每个非零对角元素替换为它的倒数并装置可以获得W+。

SM 算法求解附加函数系数如图7 所示，通过图7 的计算流程求解附加运动函数系数。理论上将运动轴的附加运动补偿到机床上，即可获得需要的齿面纹理角度。

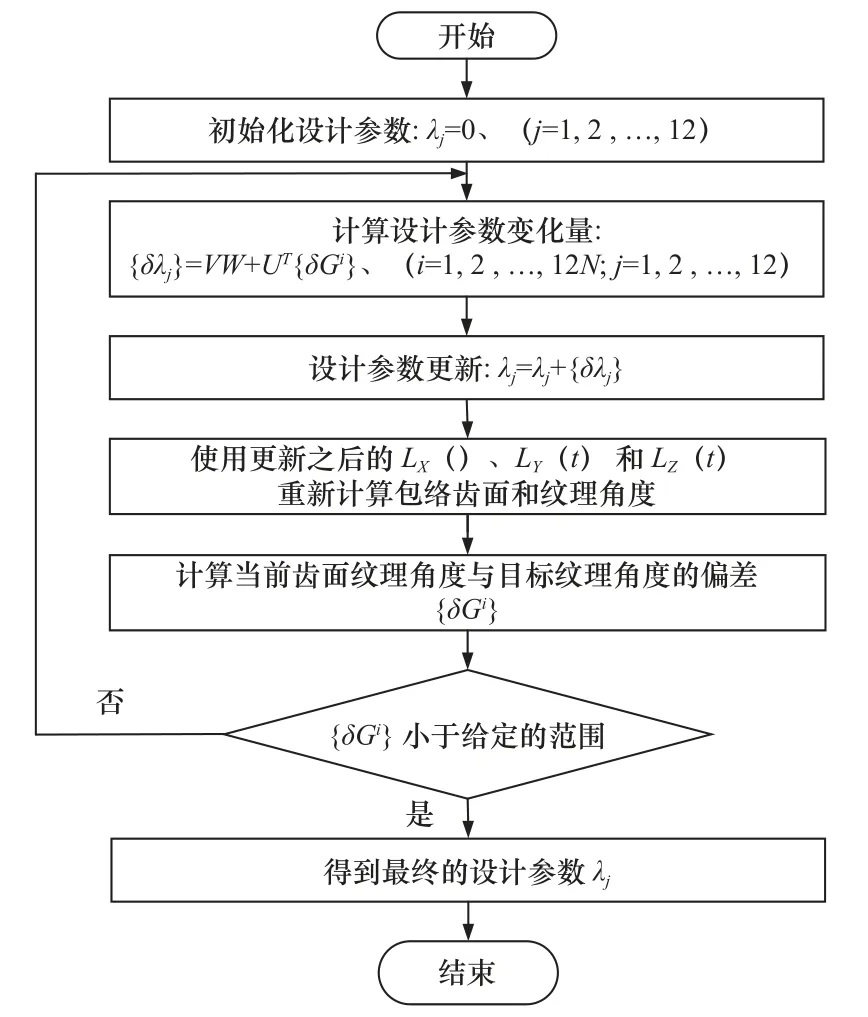
图7 附加多项式系数计算流程

3 齿面纹理仿真

以 3◦为齿面目标纹理角度，齿面网格划分为72×40，敏感度矩阵Ms如下：

前文已经建立齿面纹理角度与机床运动轴附加运动多项式系数的关系，因此可根据需要的齿面纹理角度，求得X轴、Y轴和Z轴附加运动多项式系数，见表2。

表2 附加运动多项式系数

将求得的(ti,ξi,τi)和附加运动多项式系数代入式（26），获得目标齿面的坐标以及每个点磨削印痕与齿向的夹角。然后进行齿面纹理仿真，如图8 所示。

图8 齿面纹理仿真

为了简化仿真，使用半径为dgr的球形磨粒。u为齿廓方向，v为齿向方向，h方向为齿面法向。以第n个磨粒为例，其球心为Q，与被加工齿面发生干涉，产生磨削印痕，磨削印痕的宽度为图8 中的b，弧长ljk由Malkin S[15]建立的砂轮与工件的模型可知：

磨粒干涉区域任一点在干涉截面的干涉深度hi为

式中：ri∈[0,b/2]，hs为磨粒最大干涉深度。

磨齿齿面纹理具有相似性，我们用局部纹理来表示整个齿面的纹理。Reishauer 通过设置机床的LNS 参数，使得磨削过程中附加加工运动，从而得到图9 所示的倾斜不规则的齿面纹理。

图9 采用LNS 技术的齿面纹理[11]

图10 所示为常规磨削过程产生的齿面纹理图，可以看到齿面纹理是规则的且平行于齿向的。图11所示为X、Y和Z轴附加运动后的齿面纹理。

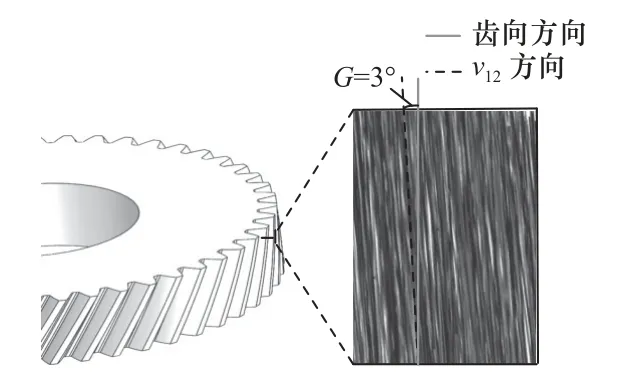
图11 X、Y 和Z 轴附加运动的齿面纹理

相比较于图10 中常规加工的齿面纹理，施加附加运动后的齿面磨削纹理分布不规则且与齿向有3◦的倾角；与图9 中采用LNS 技术获得的齿面纹理相比，也有较大的相似性，证明了本研究的可行性。

理论上，可以采用上述方法求解所需磨削齿面纹理角度的附加运动函数，在机床上对运动轴X轴、Y轴、Z轴进行补偿，即可获得所需的齿面纹理角度，实现对磨削齿面纹理的主动调控。

4 结语

（1）建立了齿轮与砂轮的模型，表示出齿轮和砂轮的坐标以及法向偏差，求得在齿轮坐标系、砂轮坐标系以及和它们固联的坐标系下，砂轮与包络齿面的坐标之间和向量之间的转化。

（2）介绍了蜗杆砂轮磨削过程中，齿面磨削纹理产生的原理，给出齿面每个磨削印痕与齿向夹角的表示方法。结合蜗杆砂轮生成包络齿面的必要条件，建立了齿面磨削纹理与运动轴附加运动的多项式系数的联系。

（3）给出目标齿面纹理角度的求解方法，即采用敏感度矩阵（SM）结合最小二乘估计（LSE）确定运动轴（X轴、Y轴、Z轴）附加运动多项式的各个系数，通过对机床进行补偿获得目标齿面纹理角度，实现磨削齿面纹理的主动调控。

（4）对齿面磨削纹理进行仿真，生成不规则的 3◦的齿面磨削纹理。与常规加工生成的齿面磨削纹理和采用LNS 技术获得的齿面磨削纹理比较，该方法可以生成倾斜不规则的磨削齿面纹理，证明了本研究的可行性。