基于NGSIM数据的高速公路客货混合车流改进跟驰模型
高云峰,赵 雪,沈 阳,罗昊涵
(1.上海海事大学 交通运输学院,上海 201306;2.上海市浦东新区规划建筑设计有限公司,上海 200125)
0 引言
高速公路是城市之间中长距离客货运输的线路设施[1]。高速公路的拥堵和安全问题随着客货运输量不断增长而日渐突出。探究高速公路客货混合车队的跟驰行为可为车流顺畅和安全运行提供理论分析和仿真分析依据。客货车辆的跟驰行为是微观交通仿真的核心模型之一,通过模拟跟驰车辆的纵向运动进而分析车队的整体运行特征。考虑到货车驾驶人对于车头间距的变化比客车更敏感,所以在研究货车比例较高的高速公路上的车辆跟驰行为时,需要考虑车头时距的影响。关于车辆跟驰行为的研究大致可归纳为以下几类。
(1)刺激反应类。刺激-反应模型将前导车对驾驶人的作用表示为一种刺激,将驾驶人的感知能力作为其对刺激的一种敏感系数,将驾驶人的反应表示为跟驰车的运动行为。作为早期出现的跟驰模型,刺激-反应模型形式简单,物理意义明确。Chandler等[2]首次提出以相对速度为刺激项的相对速度(Relative Velocity,RV)模型。RV模型简单易懂,但两车间距离很近时,后车仍然会加速,导致车辆碰撞;Gazis等[3]将速度、速度差、车头间距作为影响因素,提出了通用汽车(General Motor,GM)模型,GM模型能够较为清楚地反映跟驰车辆特性;GM模型提出后,模型标定引起了学者们的重视,如Ceder等[4]用不同状态下的交通流数据标定了GM模型。刺激-反应模型对跟驰理论的发展影响深远,许多后期的跟驰理论研究都源于刺激-反应的基本方程。
(2)安全距离类。安全距离模型是从防碰撞角度出发,利用运动学公式进行建模,也叫做防撞(Collision Avoidance,CA)模型。Gipps[5]提出的安全距离模型参数意义明确,但是缺乏实测数据的标定,在现实行车过程中很难实现;韩祥临等[6]同时考虑多辆前车和邻近后车,提出了双向耦合跟驰模型,该模型使用具有延时效应的参数,可以改善道路的交通拥堵现象;杨达等[7]新增了“相对速度”这一影响因素,构建出改进的安全距离模型,通过仿真证明了改进模型可以再现实际的交通流现象。安全距离类模型能够避免车辆之间的碰撞且模型形式较为简单,但是利用基于安全车距的车辆跟驰模型进行通行能力分析时,由于实际车距小于计算车距,很难与实际最大交通量吻合。
(3)生理心理类。生理心理类模型以驾驶人的感知和反应特性为基础,试图在跟驰行为建模中引入更多人的因素,更好地与真实驾驶行为相适应。Wiedemann[8]以行为阈值划分跟驰状态,将车辆的跟驰过程划分为自由驾驶、趋近、跟驰、减速这4种状态,该模型划分了不同的交通状态,最贴合真实的交通流;Andersen等[9]建立了视觉驾驶 (Driving by Visual Angle,DVA)模型,该模型可以很好地展现实际跟驰过程中驾驶人的个人特性。生理心理类模型充分考虑了不同交通环境下驾驶人的不同反应,从建模方法上更接近实际状况,但对各种阈值的调查测量是非常困难的。
(4)最优速度类。最优速度模型中车辆的速度即为驾驶人的理想(最优)车速。Bando等[10]提出了最优速度(Optimal Velocity,OV)跟驰模型,OV模型能够再现一些复杂的交通现象,比如停停走走的交通流、交通阻塞的演化等,但是OV模型的加减速度过高,不能描述实际的跟驰行为;Helbing等[11]改进OV模型建立了广义力(General Force,GF)模型;针对GF模型存在启动延时的缺陷,Jiang等[12]在GF模型的基础上提出了全速度差(Full Velocity Difference,FVD)模型,该模型能够更加真实地描述车辆启动过程;随后的很多学者在FVD模型的基础上提出了扩展模型,王建都等[13]考虑了多辆前导车的最优速度,建立了改进的全速度差(Improved Full Velocity Difference,IFVD)模型,该模型考虑前车最优速度影响,能更有效地抑制交通流堵塞;王涛等[14]在FVD模型的基础上构建了多速度差(Multiple Velocity Difference,MVD)模型,该模型能有效地抑制交通流堵塞并节省大量能量;黎胜等[15]在验证全速差模型的基础上,考虑安全间距和速度差对后车的加速度影响,提出了FVD的改进模型,改进模型在城市交叉路口环境中更能准确地反映车辆的跟驰行为;Gong等[16]考虑交通流中车辆速度差的不对称特性,提出了非对称全速度差(Asymmetric Full Velocity Difference,AFVD)模型;Yu等[17]基于FVD模型提出一种改进的考虑前车速度差的单车道跟驰模型,该模型与实测数据吻合较好。
(5)智能驾驶类。Treiber等[18]建立了智能驾驶员模型(Intelligent Driver Model,IDM),IDM虽然能够再现复杂的宏观交通现象,但是参数较多;Qin等[19]改进了IDM模型,使驾驶人可以提前预知道路几何信息;Lindorfer等[20]考虑驾驶人的因素改进了模型,提高了驾驶安全性能并且与实际驾驶行为十分贴合。
(6)人工智能类。驾驶人的复杂特性很难用精确的数学模型进行表达,因此人工智能的方法可以有效地描述驾驶人的这种特性。在人工智能领域,模糊逻辑、神经网络较等多应用于车辆跟驰行为建模[21-24]。人工智能类模型以数据为驱动,需要大量样本信息进行训练测试,对数据量要求也较高。
(7)元胞自动机类。元胞自动机(Cellular Automata,CA)实质上是定义在一个由具有离散、有限状态的元胞组成的元胞空间中,按照一定的局部规则,在离散时间维度上演化的动力学系统。Cremer等[25]最早将元胞自动机应用于交通流建模;Yang等[26]应用元胞自动机研究了单车道车流中的车辆跟驰行为,区分了4种汽车-卡车跟驰组合之间的差异;吴遨[27]使用连续型元胞自动机作为建模方法,引入慢启动规则并考虑了周围车辆的影响,建立了改进后的基于安全距离的交通流连续元胞自动机模型。由于CA模型与交通流复杂且不确定性的特点很相似,使得CA在交通领域的应用前景显著。
现有的跟驰模型大都基于小汽车的运动特性建立,对客货混合车流中车辆的跟驰行为研究较少,但上述车辆跟驰模型为货车比例较高的高速公路上的车辆跟驰行为研究提供了很好的基础和借鉴。本研究基于对现有模型进行改进的思路来研究高速公路客货混合车流中车辆的跟驰行为,由于其他类模型或参数标定繁杂,或者需要大量样本训练,或者仿真运算量大,本研究选取了最优速度模型进行改进。与OV模型和GF模型相比,FVD模型考虑了负速度差和正速度差的影响,所以本研究选择更符合实际情况的FVD模型进行改进,基于FVD模型构建适用于高速公路客货混合车流的改进跟驰模型。美国联邦公路局基于视频采集的NGSIM(Next Generation Simulation)数据集时间间隔为0.1 s,车辆轨迹点精度较高,并且包含了车型信息、位置信息、速度信息、加速度信息,为标定和验证改进跟驰模型提供了较理想的数据。
1 改进跟驰模型构建
在客货混合车流中,由于货车的刹车距离比较长,所以货车的加减速行为不但与速度差有关,而且与车头间距有关。混合流中客车的加减速行为满足经典的FVD模型,其具体表达式为:
an+1(t)=α{V[Δxn(t)]-vn+1(t)}+β[Δvn(t)],
(1)
式中,α为跟驰车辆的敏感系数;β为对速度差项的反应系数;Δxn(t)为跟驰车辆在t时刻的车头间距;Δvn(t)为t时刻前导车与目标车之间的速度差;V[Δxn(t)]为目标车的最优速度函数。
FVD模型中,车头间距只是作为一个间接因素影响驾驶人的期望速度。在客货混合车流中,由于货车的加减速性能较差,刹车距离比较长,货车驾驶人更加注意与前车保持合适的车头间距。因此,本研究在FVD模型的基础上引入车头间距项的反应系数γ,将车头间距Δxn(t)作为直接作用项,构建考虑前导车多信息的改进跟驰模型。车辆跟驰过程中,混合流中第n+1辆货车的加减速行为满足本研究构建的基于FVD模型的改进跟驰模型,其表达式如下:
an+1(t)=α{V[Δxn(t)]-vn+1(t)}+β[Δvn(t)]+
γ[Δxn(t)],
(2)
式中γ为对车头间距项的反应系数。最优速度函数采用如下形式:
(3)
式中,Vf为自由流速度;hc为系数。二者均为待标定参数。
2 改进跟驰模型参数标定
2.1 NGSIM数据说明及预处理
视频检测及研究区域长约500 m,5条主干道中包括1条HOV车道,第6车道为出入口匝道。研究数据来源于NGSIM数据集提供的80号州际公路(Interstate 80,I-80)广域探测器数据,共收集了6个监测站点(1,3,4,5,6,7号监测站)10 d(2005-04-07至04-20)的环形探测器数据。图1为研究区域内检测器位置示意图。
NGSIM数据集中每一行记录了某时刻某一车辆的驾驶数据,截取I-80部分数据并且随机以一条数据为例,从左至右对每一标签的意义进行说明。具体说明见表1。
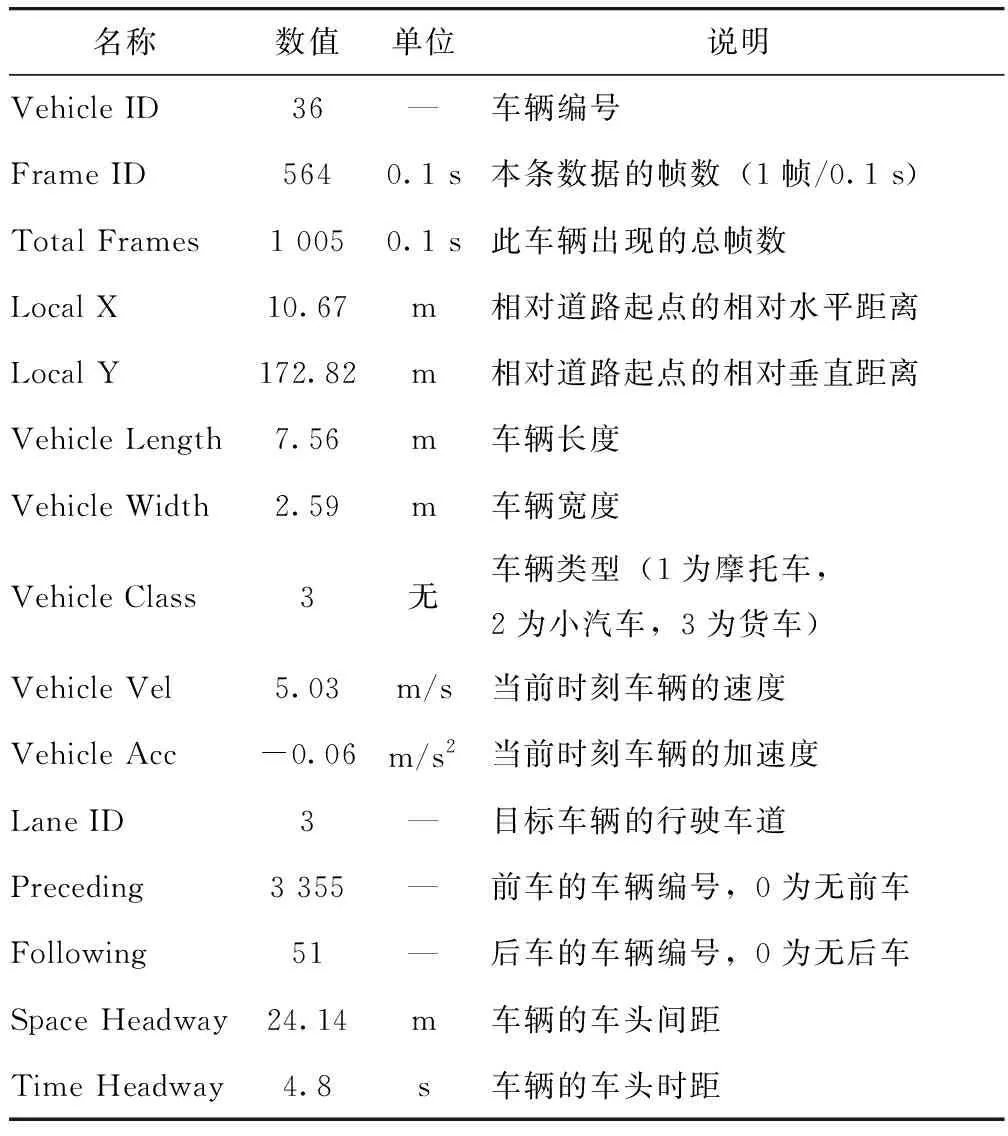
表1 NGSIM数据说明Tab.1 Description of NGSIM data
NGSIM数据集中每辆车都有前车和后车的ID,即提供了对象车辆的前导车和跟驰车的信息。本研究选取I-80路段的数据子集的时间段为16:00—16:15,17:00—17:30,为道路拥堵过渡期和全面拥堵时段。NGSIM数据存在测量或观测误差,导致了一些随机噪声,在筛选之前对跟驰车辆的位置和速度进行移动平均去噪处理,位置和速度的移动跨度分别为0.5 s和1 s,数据处理过程见图2。

图2 数据预处理流程Fig.2 Process of data pre-processing
此外,NGSIM的原始数据量很大,需要对I-80数据集进行筛选,筛选原则如下:
(1)跟驰车道。所选的跟驰车辆必须在同一车道上,由于车道1为合乘车道(High Occupancy Vehicle,HOV)车道,6个车道存在较多的车道变换行为,所以本研究选择车道3为研究对象,即“Lane ID”=3。
(2)车辆速度。过滤掉速度低于4 km/h的数据,认为低于此值时车辆处于停止状态[28]。
(3)车头间距。跟驰状态临界值的判定是研究车辆跟驰行为的一个关键[29-31]。顾海燕[31]指出跟驰行为发生在两车车头间距为0~100 m或者0~125 m范围内,本研究把100 m作为跟驰状态的最大界限,“Space Headway”的范围为[0,100]m。
(4)跟驰时间。为保证有效样本的时间间隔一致,取持续跟驰时间为33 s[31]。
经过筛选和处理,共输出58 930条数据,这些样本数据将用于参数标定。
2.2 参数标定方法
改进跟驰模型需要标定的参数有α,β,γ,Vf,hc。目前,跟驰模型参数标定主要有2种方法[32]:极大似然估计法和最小二乘参数标定法。本研究采用最小二乘参数标定法,以均方根误差值最小为目标,使标定模型最大程度吻合实测数据。在改进跟驰模型中,加速度作为输出目标,其目标函数如下:
(4)
本研究应用遗传算法求解改进跟驰模型的参数,在全局范围内搜索待标定参数的最优解,详细过程如下:
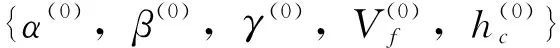
(2)计算适应度值。如图3所示,将M个样本数据中的车头间距、速度、速度差等实际数据带入式(2)和(3),分别求出模型输出的模拟加速度值ai。计算每个个体的适应度值F并保留精英个体:
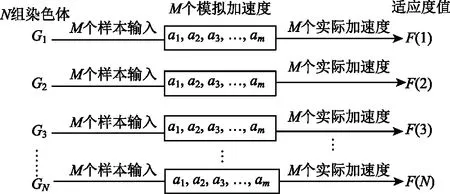
图3 适应度计算过程Fig.3 Process of fitness calculation
(5)
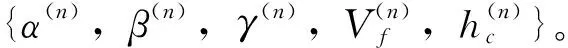
(4)终止条件判断。若迭代到最大次数,就停止迭代,否则要返回第2步。
2.3 参数标定结果
给定待标定参数的范围α∈[0,1],β∈[0,1],γ∈[0,1],Vf∈[16,50],hc∈[0,100][33],设置种群数为60个,交叉概率为0.6,变异概率为0.1,进化代数为200次。标定结果如图4所示,算法在第97代收敛,最佳适应度值为6.04。参数标定的结果为α=0.41,β=0.24,γ=0.265,Vf=38.3,hc=7.29。
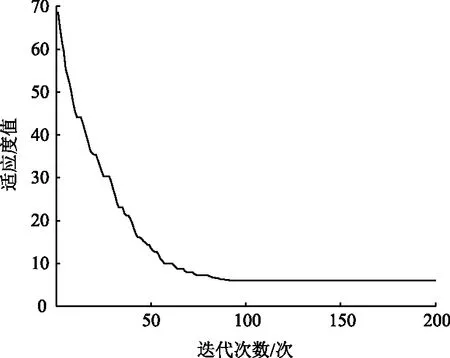
图4 标定过程收敛曲线Fig.4 Convergence curve of calibration
3 改进跟驰模型验证与分析
3.1 与FVD模型对比
(1)误差对比分析
在NGSIM数据集中选取I-86公路上第86号目标车辆跟驰第51号前导车的轨迹数据对本研究的标定结果进行验证。本研究采用平均绝对误差(MAE)和均方根误差(RMSE)作为评价指标,计算公式如下:
(6)
(7)
表2是通过拟合加速度与实际加速度计算出的平均绝对误差和均方根误差值,可以看出改进模型与实际数据的吻合程度更好,在刻画实际交通流的效果方面优于FVD模型。
(2)稳定性对比分析
改进跟驰模型的参数取值均为标定结果。FVD模型的参数取值为α=0.41,β=0.2。对第40号车施加扰动,使该车行驶速度在0时刻突然降低,则扰动随仿真时间增加向后方车辆传播。为了对比FVD模型和改进模型的致稳性,分别观察改进跟驰模型和FVD模型关于第40,50,60和70号车的跟驰距离的仿真结果。
由改进跟驰模型的仿真结果可以看出,由于仿真开始时刻第40号车的速度降低,导致了与前车的距离增加,所以0时刻车头间距瞬间增大。第40号车的扰动幅度最大,跟驰的第50,60和70号车的间距扰动逐渐降低。第70号车辆的跟驰距离基本维持在8 m左右,扰动传播至第70号车基本消散,车流恢复平稳运行状态。这说明了改进跟驰模型能很好地模拟扰动的“消化”过程,对个别车辆的微小扰动在向后传播过程中在车队内部被“消化”,即扰动能够在后向传播过程中自行吸收消散,所以改进跟驰模型的稳定性表现较好。
然而,FVD模型从扰动向后传播的过程可以看出,扰动从第40~50号车的传递过程,扰动效应被放大,车头间距一直在3~13 m之间频繁变化,表现出时走时停现象,即车流发生局部拥堵。随着仿真过程推移,第60和70号车的跟驰距离波动幅度变小,可以看出扰动逐渐被抑制。
对比仿真结果可发现改进跟驰模型在抗干扰能力上强于FVD模型,能够很平顺地抑制车头间距的随机波动,保证下游车辆正常行驶和车队稳定运行。而FVD模型在扰动传播的前期会造成时走时停(局部拥堵)现象,且扰动的作用时间较长,所以改进跟驰模型具有较好的稳定性。
3.2 微观跟驰特性验证
为研究客货混合流跟驰时车速和车头间距的关系,本节利用实际跟驰数据进行拟合。同时为了验证改进跟驰模型是否能准确描述微观跟驰行为,把改进跟驰模型仿真输出的速度和车头间距的关系曲线与实际数据的拟合曲线进行对比,结果如图5所示。
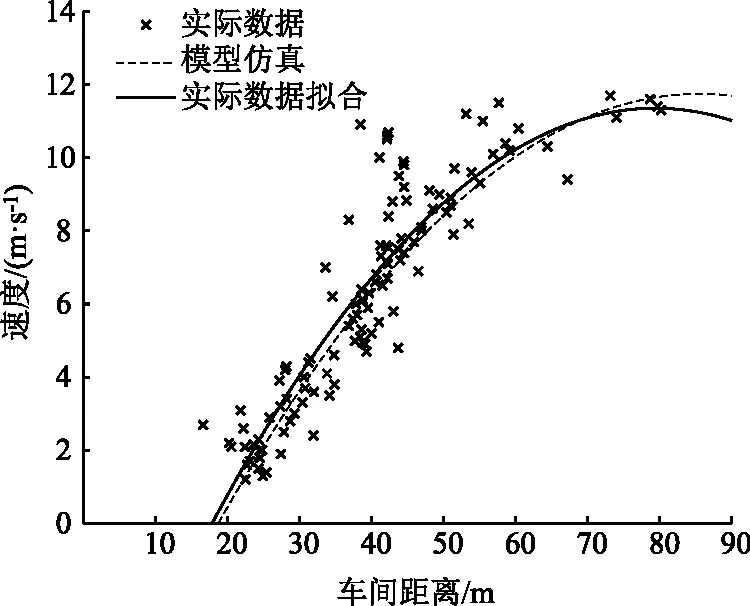
图5 改进跟驰模型输出的仿真曲线与实际数据拟合曲线对比Fig.5 Comparison between simulation curve output by improved car-following model and fitting curve of actual data
如图5所示,客货混合流跟驰的速度在2~12 m/s 之间,这是因为拥堵时段内试验路段上的平均车速较低。车头间距主要分布在20~60 m区间内,处于60~80 m区间内的数据点较少。车速随着车头间距的增加而增加,在密度较小区间内速度的增长率逐渐降低趋于平缓。改进跟驰模型的仿真曲线与实际跟驰数据的拟合曲线变化走势一致,仿真结果与实际数据的拟合精度较好,说明改进跟驰模型可以准确反映客货混合流在跟驰状态下速度与车头间距的真实关系,即改进跟驰模型能够较好地刻画实际客货混合流的微观跟驰特性。
3.3 宏观交通流特性验证
跟驰模型是宏观交通流运行规律与微观交通特性的连接桥梁,宏观交通流参数关系也是研究跟驰模型的重要内容[34]。以下通过仿真宏观客货混合流交通参数间的关系与I-80道路的宏观交通流运行特征进行对比。
(1)速度-密度特性
根据实际混合流数据拟合得到的速度-密度(u-k)函数为:
(8)
改进跟驰模型所描述的速度-密度关系曲线和实际混合流数据的拟合曲线如图6所示。
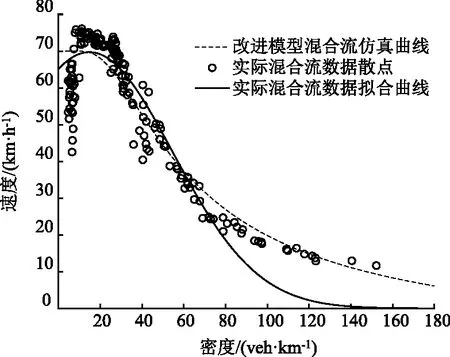
图6 实际混合流与改进跟驰模型仿真的混合流速度-密度关系对比Fig.6 Comparison of speed-density relationship between actual mixed flow and improved car-following model
由图6可以看出改进跟驰模型描述的混合流的速度-密度关系与实际的混合交通流存在差别。在自由流状态下,当道路密度低于10 veh/km时,实际混合流的拟合曲线表明车速随着密度的增加而略微增加,而当改进仿真模型输出的车速达到理想速度(畅行速度)后,它不会再随着密度的增加而增加。当道路密度为10~60 veh/km时,同一密度所对应的实际混合流平均车速高于改进跟驰模型输出的混合流平均速度。但当密度为55 veh/km以上时,改进跟驰模型输出的混合流的平均速度高于实际混合流的速度。这可能是由于当路段上车辆密度较高时,实际的客货混合交通流内部存在的扰动等异常情况更为复杂,驾驶人的不确定反应和操作等都可能降低车流的平均速度。
(2)流量-密度特性
同样地,对实际混合流数据进行拟合可以得到实际混合流与改进跟驰模型仿真得出的混合流流量-密度对比图(见图7),其中,实际混合流数据的流量-密度(q-k)拟合关系式为:
q=3 014e-0.005k-3 616e-0.05k,R2=0.957 4。
(9)
由图7可知,利用改进跟驰模型仿真得出的流量-密度关系与实际混合流的流量-密度关系的走势完全一致。当密度低于50 veh/km时,流量随着密度的增加,几乎呈现线形增加的趋势,当密度超过50 veh/km后,流量随着密度的进一步增加而逐渐降低。实际混合流在50.5 veh/km处达到最大交通量2 120 veh/h,而改进跟驰模型在58 veh/km处达到最大交通量2 250 veh/h。
3.4 敏感性仿真分析
为了分析对车头间距项的反应系数γ对于改进模型的影响,本研究将一个车队置于单车道来进行仿真试验。
(1)初始状态设定
假设一个车队有100辆车(N=100)分布在长为4 000 m的单车道上,车头间距b为13 m。初始状态下所有车辆都保持稳定的跟驰状态,即保持相同的行驶速度和相同的跟驰距离。最优速度函数项的敏感系数α为0.41,初始稳态下每辆车的加速度均为0 m/s2,速度均为8 m/s。假设头车编号为1,尾车编号为100。初始状态下,车辆的位置为xn(t)=(n-1)b,其中n为1,2,…,100。车辆在位移中的速度更新表达式为:
vn=vn-1(t)+an-1(t)τ,
(10)
xn=xn-1(t)+vn-1(t)τ+0.5an-1(t)τ2,
(11)
式中τ为仿真步长,取0.1 s。假设在仿真开始时,第40号车的车速突然降低1/2,扰动产生。
(2)灵敏度分析
不同类型的驾驶人对车头间距的关注程度是不同的。为了验证γ对跟驰稳定性的影响,本节研究了γ分别为0.1,0.2,0.3时,车队在第500,1 000和1 500 s仿真时刻车队车辆的车头间距波动情况,具体见图8。
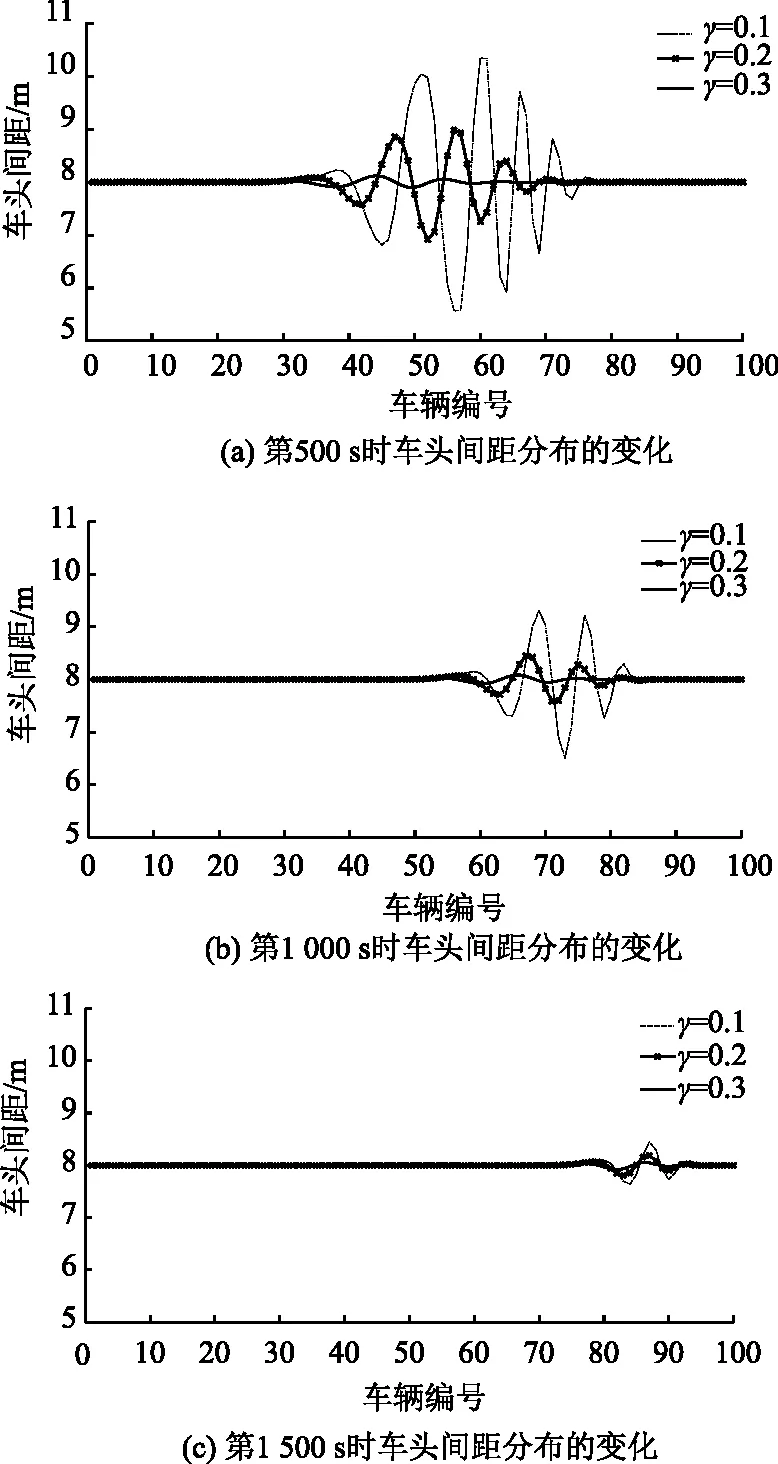
图8 不同γ值下各仿真时刻的车头间距分布Fig.8 Distribution of space headway at each simulation time under different γ values
图8演示了扰动的后向传播过程。γ=0.1时扰动的幅度最大,γ=0.2时扰动的幅度有所降低,γ=0.3时车队受到的影响最小。当扰动的波动率在3%以内时,则认为系统恢复至稳定状态。为了具体说明引入的车头间距项对波动幅度的影响,分别给出γ=0.1,0.2,0.3时车辆的车头间距波动情况(见表3)。
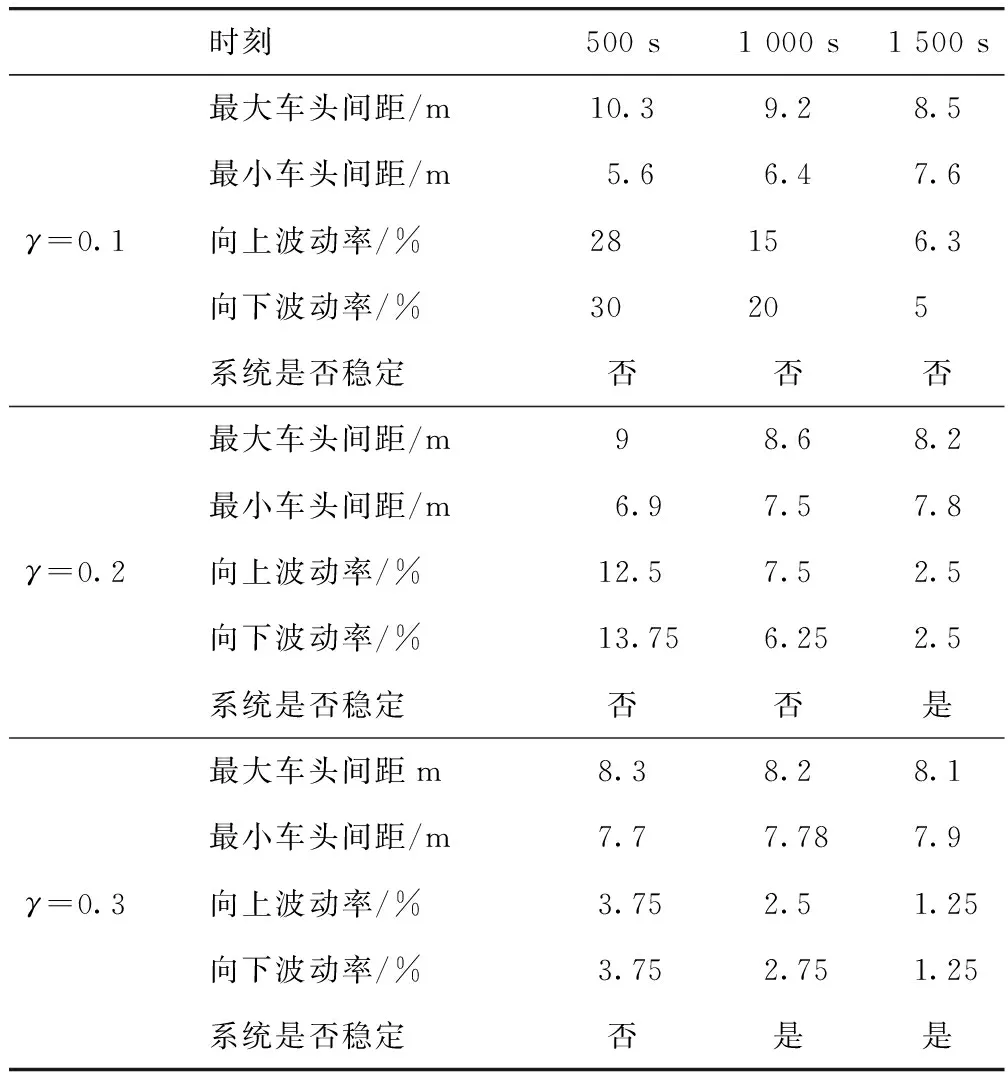
表3 改进跟驰模型不同时刻的车头间距及其波动率Tab.3 Space headway and its volatility of improved tracking model at different times
根据表3可知,相同γ值下,车辆车头间距的波动率随着时间的增加逐渐减少。γ值增加,意味着驾驶人对车头间距的关注度提高,驾驶人越能够更准确地判断前导车的速度变化,并及时做出正确决策。γ值增大后,车队恢复至稳态的时间越短,自愈能力更强。
4 结论
由于货车驾驶人对车头间距的变化更敏感,本研究提出的改进跟驰模型可用于描述高速公路客货混合车流中货车的跟驰行为。考虑到车头间距也是影响驾驶行为的一个不可忽略因素,本研究对全速度差(FVD)模型进行了改进,增加了车头间距直接作用项,并基于NGSIM数据进行了参数标定和验证。
FVD模型中,车头间距只是作为一个间接因素影响驾驶人的期望速度。在客货混合车流中,由于货车的加减速性能较差,刹车距离比较长,货车驾驶人更加注意与前车保持合适的车头间距。因此,本研究在FVD模型的基础上引入车头间距项的反应系数,将车头间距作为直接作用项构建改进跟驰模型。该模型用来描述“混合车流”中的货车跟车行为,而混合车流中的客车依旧使用经典的FVD模型来描述其跟车行为。
利用货车跟驰的实际数据分别对优化速度函数和改进的模型进行参数标定,标定的验证结果表明改进的跟驰模型对实际跟驰数据有较高的拟合精度,改进模型在刻画货车跟驰行为的效果上优于FVD模型,进一步说明了改进的FVD模型更适合描述客货混合车流的运行特征。
通过本研究的拟合分析,进一步得到如下结论:
(1)与FVD模型相比,改进跟驰模型的稳定性更好,能很好地模拟车队的扰动“消化”过程;
(2)经过标定的改进跟驰模型的仿真结果与实际数据的微观统计特征的吻合程度较高,与实际数据的宏观拟合结果的变化趋势一致;
(3)车头间距直接作用项的敏感系数取值大小与受内部干扰后车队恢复至稳态的时间长短密切相关,γ值越大,驾驶人对车头时距变化的敏感度越高,车队受扰动后恢复至稳态的时间越短。
本研究提出的改进跟驰模型可应用于疏港公路客货混合车流的模拟。由于试验条件限制,本研究仍存在不足之处,例如由于本研究的NGSIM数据时间跨度较小,混合流中的客货车混合比例固定,无法进一步探讨客货车混合比例对客货车混合车流跟驰行为的影响。今后可在以下方面继续探索:(1)采集国内疏港公路上的跟车数据,基于国内数据标定改进跟驰模型并分析其适用性;(2)考虑无人驾驶车辆与有人驾驶车辆共存的场景,研究改进跟驰模型的适用性;(3)基于我国公路不同客货车比例的跟车数据,进一步研究不同客货比例对于本研究跟驰模型仿真结果的影响。

