大滞后固井系统预估补偿控制算法研究

刘启蒙，贾 涛，崔俊国，康和邦

（1.宝鸡石油机械有限责任公司，宝鸡 721000；2.中油国家油气钻井装备工程技术研究中心有限公司，宝鸡 721000；3.中国石油大学（华东）机电工程学院，青岛 266580）

在油田开发过程中，固井作业是相对独立的工程体系，具有作业时间短、工序多、技术性强，以及隐蔽性、一次性、风险大等特点。固井质量关系到油气田的合理开发、后续井下作业的顺利进行，是油气井的“百年大计”。固井要解决的核心问题是怎样加强井壁与套管间水泥环的密封质量。因此，在固井时使用的水泥质量对完井后的井质有着很重要的作用。近年来随着社会经济的发展，世界对能源需求不断增大，推动油气田勘探和开发技术不断发展，固井技术在诸多方面取得了一系列成果，逐渐形成了调整井固井技术、双密度固井技术、双极注固井技术、尾管固井技术、深井固井技术、小井眼固井技术、水平井固井技术、膏岩层固井技术、泡沫水泥浆固井技术等，基本满足国内各油气田对固井工程技术的需要，但世界对能源的需求与日俱增，迫使油气田的勘探开发技术持续向前，钻井和固井的效率和质量仍有较大发展空间。

1 大滞后系统分析

目前，油田作业中固井混浆控制过程中存在大滞后问题，即反馈控制长时间滞后于扰动。滞后现象在被控对象的传递函数中可被表示为一个滞后环节，因为该滞后环节的存在，尽管控制器已发出控制量改变指令，但由于传输延时，执行机构无法立即响应，从而被控量不能及时跟随控制量变化，导致控制器产生的控制效果在一定时间延迟后才能到达目标被控对象，这个过程中输出量容易产生较大超调量，调节时间也会更长，最终使控制质量不佳，控制效果变差，甚至引发输出信号振荡和发散[1-3]。

一般用滞后系统的滞后时间常数τ 和积分时间常数T 之比τ/T 来衡量滞后对系统的影响。例如对于一阶被控系统，当延迟时间因子和时间常数的比τT<0.3 时，是常规时滞系统，可用常规的PID 等控制方法对系统进行控制；而当τT>0.3 时，可视为大时间滞后系统，随着滞后时间常数τ 所占比的增大，其控制难度会逐渐增大。

目前，固井混浆装备的控制方式是PID 控制。PID控制器是将偏差比例（Proportion）、积分（Integral）和微分（Differential）通过线性组合构成控制量，用这一控制量对被控对象进行控制。PID 虽然结构简单，但参数整定方法却没有固定规律可循，主要依赖于施工人员的经验，不利于提高生产效率，其中较广泛使用的位置式PID 控制器输出控制量与过去每个时刻的误差量相关，过去的每个状态都决定着当前时刻的输出值。因为单纯依靠PID 进行控制的系统是按被控参数与给定值的偏差进行控制的，其特点是在被控参数出现偏差后，调节器发出控制命令以补偿扰动对被控参数的影响，最后消除（或基本消除）偏差。若扰动已经发生，而被控参数尚未变化，则调节器将不产生校正作用。所以，反馈控制总是滞后于扰动，是一种不及时的控制，会造成调节过程的动态偏差；同时在控制过程中会产生积分饱和现象，即当系统的控制量已经达到最大值时，误差依然会在积分的作用下继续累加。一旦误差开始反向变化，则系统会进入饱和区，并且需要较长时间才能从饱和区退出。故而对于此种大时滞情况，控制质量较差，需要较长时间才能达到稳定。

由此可知，针对固井混浆控制系统，需要在传统PID 方法上加以改进，通过采用预估补偿的自主控制算法，由预估器进行补偿，消除系统模型中的延时环节，使被延迟了τ 秒的被控量超前反馈到控制器，控制器提前动作，使改变后系统的控制通道以及系统传递函数的分母不含有纯滞后环节，被延时的信息能及时送入系统执行部分，从而减少系统超调量和响应时间，消除时滞的不利影响，实现液位和密度控制的稳定性及快速响应，提高快速响应及抗干扰能力。

2 控制算法研究

固井混浆控制方法通过调节干灰计量阀自动控制泥浆密度，通过调节清水比例阀来控制清水吸入流量，从而来调整泥浆液面位置。目前，固井过程控制方式是数字式PID 控制，而数字式PID 控制分为位置式PID 控制和增量式PID 控制。其中位置式PID 实用性较好，如图1 所示。

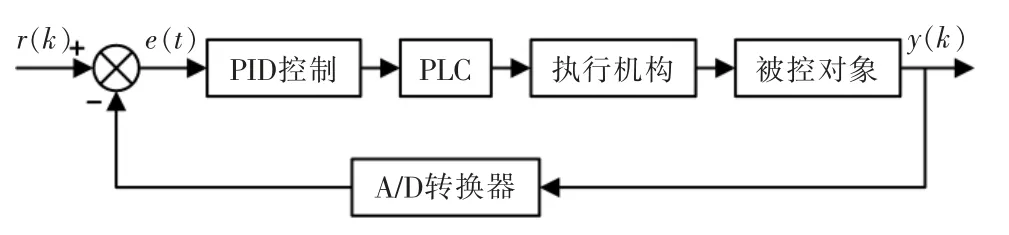
图1 位置式PID 控制系统原理图Fig.1 Position type PID control system schematic diagram

2.1 传统PID 控制系统

PID（proportion integration differentiati）控制是通过测量、比较和执行3 方面来综合调节控制。日趋成熟的PID 控制以其算法简单、操作灵活、可靠性较高和适应性较强为特点，已成为目前最常用的控制方法之一。当对象特性发生较大变化时，控制系统仍具有相当强的稳定性和鲁棒性。早期PID 多为模拟PID 控制器，其系统原理如图2 所示。PID 控制器主要包括2 个部分，用来对偏差值进行计算的模拟PID 控制器，和计算后输出控制量控制被控对象2 部分组成。

图2 传统PID 控制器原理框图Fig.2 Traditional PID controller principle block diagram

2.2 Smith 预估控制系统

针对大滞后系统的控制问题，Smith 预估控制是目前工业上广泛应用的方案之一。Smith 预估控制原理框图如图3 所示。其设计思想是在控制系统中加入Smith 预估补偿器，由预估器进行补偿，消除系统模型中的延时环节，使被延迟了τ 秒的被控量超前反馈到控制器，控制器提前动作，使改变后系统的控制通道以及系统传递函数的分母不含有纯滞后环节，被延时的信息能及时送入系统执行部分，从而减少系统超调量和响应时间，消除了时滞的不利影响[4-5]。

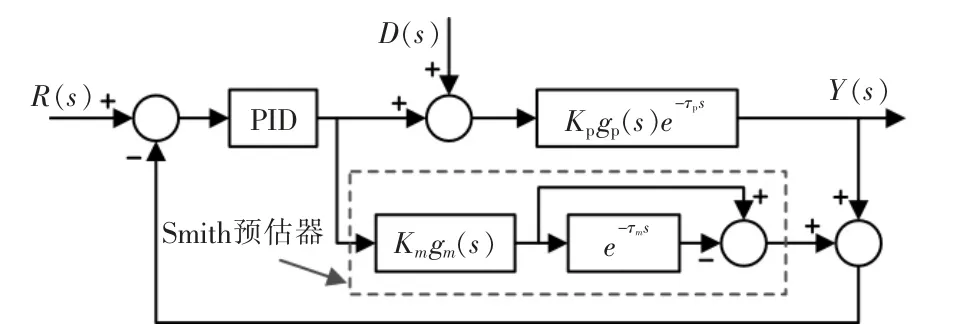
图3 Smith 预估控制器原理框图Fig.3 Smith estimated the controller schematic diagram

2.3 Smith Fuzzy-PID 控制

Smith Fuzzy-PID 控制系统结构如图4 所示。该控制器由模糊自整定PID 控制器与Smith 预估控制器组成，结合了Smith 控制和模糊控制的优点，模糊控制克服被控对象数学模型时变、不确定性，Smith控制克服被控对象的纯滞后环节和网络时延对系统控制性能不利的影响，从而改善了网络控制系统的控制性能。Smith 预估控制器来消除纯滞后环节；模糊控制器以给定输入信号与主反馈信号的偏差e与偏差变化率ec 为输入变量，以PID 控制器的比例、积分、微分调节参数的变化ΔKp、ΔKi、ΔKd为输出变量，运用模糊推理法在线修正PID 的3 个参数，来满足不同时刻的偏差e 与偏差变化率ec 对PID参数的要求；PID 控制器依据调整后的参数来输出控制量，进而对下灰阀开度进行调节。

图4 Smith Fuzzy-PID 控制器原理框图Fig.4 Smith Fuzzy-PID controller principle block diagram

如图4 所示，自适应模糊Smith 控制器主要由模糊PID 控制器及Smith 预估器2 部分构成。其中，模糊PID 控制为主控制器。控制系统中含有被控对象的纯滞后时间τ，由Smith 预估器对其进行补偿，也就是说，直接利用Smith 预估器补偿被控对象的纯滞后时间τ。滞后环节的存在使系统的相位出现滞后，随着滞后时间的增加，相位滞后增加，系统的稳定性降低，产生超调或者振荡，导致控制质量下降，Smith 预估控制就是为了提高这类系统的稳定性。从现实操作出发，实际的Smith 预估器通常不是并联在被控对象上的，而是反向并联在控制器上的，故而在控制器的两端反向并联一个反馈补偿网络。补偿后的系统框图如图5 所示。

图5 工程应用时Smith Fuzzy-PID 控制器原理框图Fig.5 Engineering application Smith Fuzzy-PID controller principle block diagram

图5 中，Smith 预估器与模糊PID 控制器Gc（s）共同构成自适应模糊Smith 控制器。其传递函数为

整个闭环系统的传递函数：

引入Smith 预估补偿器后系统的特征多项式中已不含e-τs项。

由以上分析可知，Smith 预估器的实质就是利用被控对象的模型，使控制过程的品质达到类似过程无纯滞后的情况，其优越性在于能将延时部分从过程传递函数的闭环部分中分离出来，使系统的动作灵敏，过渡过程缩短，超调量减小，很好地改善了系统性能。考虑到实际应用当中，网络时延具有不确定性，设计控制器时采用模糊PID 与Smith 预估器组合，控制器不仅能补偿网络时延对控制系统产生的不利影响，同时在系统网络时延发生变化时利用模糊PID 控制器的抗干扰性，保证了系统稳定性。

3 仿真分析

3.1 建立传递函数

设定密度与实际检测密度构成单回路反馈闭环控制，通过控制调速装置控制加灰量，达到密度控制的目的。系统控制过程中密度计检测到密度不断变化，直至相对稳定，此环节视为一阶惯性环节；从控制信号到对系统的控制之间存在滞后，此阶段为纯滞后环节；因此该系统是具有纯滞后的一阶惯性环节，其传递函数形式如下：

式中：K 为比例系数；T 为惯性环节的时间常数；τ 为纯滞后时间。

取被控对象的传递函数为

3.2 传统PID 仿真

借助MATLAB/Simulink 中的标准模块快速、准确建立控制系统的仿真模型，并进行输出结果仿真。采用PID 控制，其控制结构原理如图6 所示，仿真图如图7 所示。

图6 PID 的Simulink 仿真结构Fig.6 PID Simulink simulation structure

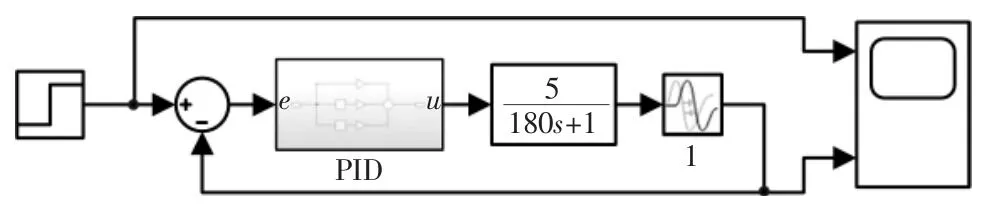
图7 PID 控制系统仿真图Fig.7 PID control system simulation diagram

传统PID 控制响应较快，上升时间较短，能较快达到设定密度，且调节过程平稳，稳态性能较好，缺点是存在较大的超调，达到稳态所需的时间较长，响应速度略缓慢。

3.3 Smith 预估补偿控制仿真

Smith 预估对模型的精度要求较高。即使建立成功，模型也可能存在失配问题，达不到预期控制效果。同时工业现场系统又存在时变和扰动现象，都限制其实际应用范围。当模型不精确或存在负荷扰动时，例如滞后失配时，系统将变为以经典PID 为控制器，以时滞对象与无时滞对象并联反馈的复杂系统，破坏了Smith 预估的滞后控制补偿机理。有关被控对象的相关知识和信息的不全或者其本身的复杂性将导致结构和参数估计的偏差，控制过程中被控对象的参数也可能随时间发生变化产生动态偏离。这些因素带来的预估器模型和被控对象的结构和参数的不匹配将引起系统控制特性的急剧劣化甚至发生系统的不稳定。MATLAB 仿真结构如图8 所示。

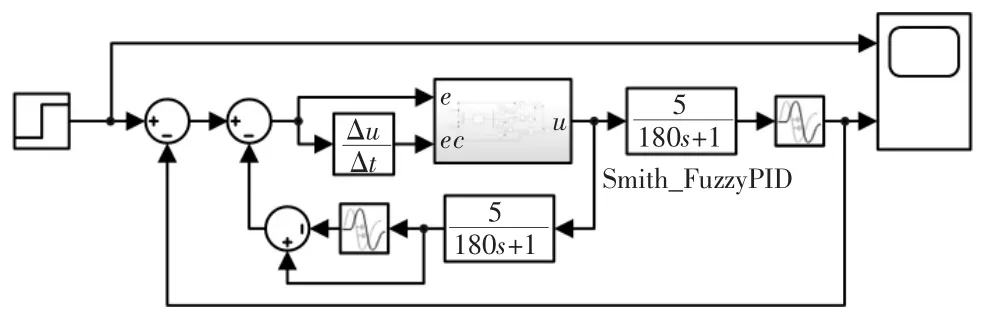
图8 Smith 预估补偿控制系统仿真图Fig.8 Smith predictive compensation control system simulation diagram

Smith 预估补偿控制上升时间较短，稳态性能较好，存在超调但不严重，达到稳态所需的时间较长，响应略缓慢。

3.4 Smith Fuzzy-PID 控制仿真

在模糊控制的基础上加入Smith 控制，便是将Smith 预估控制的输出Ym（s）作为反馈量反馈至前端，此时模糊PID 的输入（e）的计算方法是在密度设定值减去密度计实测值的基础上，进一步减去Smith 输出Ym（s），将此结果作为误差e 的值进行后续计算。

采用Smith-FuzzyPID 控制的系统，无超调现象发生，上升时间短，且稳态性能最好，可以实现令人满意的控制效果。

4 结语

综上所述，借助Simulink 分别对以上3 种控制算法进行系统建模并进行动态仿真，结果表明：传统PID 控制上升时间比模糊控制短，且静态性能好，但超调量大；Smith 预估补偿控制同前二者相比上升时间较长，但超调量较小；Smith-Fuzzy PID 控制的优点在于未发生超调现象，加入模糊PID 控制，与传统PID 控制相比具有良好的动态性能，上升时间较短，超调量较小，且稳态精度高。