基于Simulink 的直流电动离心泵动态系统建模及控制系统设计

耿胡锐，许继洋，汪自成，田梦媛

（1.武汉工程大学 机电工程学院，武汉 430205；2.武汉市光谷第六小学，武汉 430073）

离心泵是一种机械复杂度较高、噪音大、结构复杂、使用寿命较长，功率较大的装置[1]，以旋转形式产生压力，被广泛运用于许多工业领域。其中，离心泵在船舶系统中主要运用于船舶的诸如消防、压载、排水等各种系统中[2]。在实际生产生活中，进行产品设计前，运用计算机仿真可极大地减少资源的消耗。利用这项技术，可以实现由计算机取代人类进行工业制造生产[3]。若想利用计算机进行实际系统的仿真工作，完成实际系统数学模型的建立这一步骤必不可少。

目前，国内学者对离心泵系统的研究主要采用三维建模加数值模拟或有限元分析的方式。文献[4]利用Solidworks 软件建立了泵体和叶轮的三维模型，在雷诺时均方程和RNG k-εt 湍流模型的基础上，获得了内流场的静压和速度分布情况；文献[5]通过对离心泵零件网格划分的研究，得到了一种精确、高效、实用的有限元建模方法；文献[6]完成了离心泵系统中基于内特性和外特性的离心泵的动态建模方法，并给出了其在水泵启动过渡过程中的应用；文献[7-8]完成了基于外特性的离心泵系统启动过程动态建模的过程，并结合相似理论和泵机组动力学特性建立了离心泵启动过程的数学模型。

根据对实际系统的理论建模的4 个步骤，在完成数学模型建立之后需对数学模型进行分析求解，然后进行仿真使计算结果可视化[9]。Simulink 是美国Mathworks 公司推出的MATLAB 中的一种可视化仿真工具，用于多域仿真以及基于模型的设计。Simulink提供图形编辑器、可自定义的模块库以及求解器，能够进行动态系统建模和仿真，由于其模块的丰富性，被广泛应用于各类工业设备和科学研究等方面[10]。

以上研究或完成了离心泵或离心泵系统的理论建模，或利用有限元分析软件和三维建模软件等工具针对离心泵进行了流体分析等工作，未完成从实际模型到理论模型建立再到控制系统搭建的完整步骤。本文运用MATLAB/Simulink 工具，完成了2种典型离心泵系统动态模型的构建，并针对其中一种典型系统完成了完整的控制系统设计的工作，考虑了实际系统中液位变化的极端情况，添加了示警模块，为离心泵控制系统的进一步研究提供了理论支撑和研究思路。

1 离心泵抽水系统的数学模型

数学模型是根据物理和流体力学的基本定律，通过设备的动态分析得到的[11]。本部分所研究的泵系统主要由高速直流电机、离心泵和恒定液位的水箱组成。系统数学模型的确立包括离心泵数学模型的建立和水箱数学模型的建立。水箱内不断接收输入流量为Qv1的液体，通过控制阀的输出流量为Qv2。该泵系统的功能方案如图1 所示。

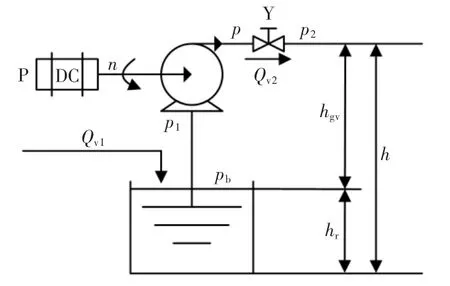
图1 泵系统功能方案Fig.1 Pump system functional plan

1.1 离心泵数学模型的建立类比牛顿第二定律：

力矩M、角速度ω、加速度a、转动惯量l 之间的关系如下：

类比以上公式可知角加速度与轴上力矩成正比，因此，电机上力矩平衡方程可表述为[12]

式中：J 为转动惯量（具体为一比例常数）；MDC为直流电机主动转矩；MP为泵的被动/电阻转矩；Mζ为粘性力矩。

设直流电机的额定（输出）功率为P（单位：kW），额定转速为n（单位：r/min），直流电机转矩可表述为

泵的被动转矩Mp和粘性力矩Mζ可分别表述为

离心泵基本参数为泵流量Qv、扬程H、角速度ω，泵流量可用叶轮周边截面和子午速度分量来表示，因此流量与角速度成正比，故在泵效率系数为常数时，对于不同的操作模式有以下规律：

式（9）适用于任意两种操作模式，将式（7）、式（8）代入式（9）中可得：

由式（10）可知离心泵的被动转矩与流量Qv2和角速度ω 成正比。

离心泵特性曲线包括Qv-H 曲线（流量-扬程曲线）和Qv-η 曲线（流量-效率曲线）2 种[13]。由于离心泵动力学的复杂性，可以假设Qv-H 曲线具有足够的精确度来描述泵在过渡状态的工况，即使用泵的静态特性。离心泵的特性曲线可用以下方程描述：

式中：A、B、C 为不同型号泵的特性常数。式（11）为一参数为ω 的抛物线族，即该表达式决定了离心泵的静态特性族。根据式（11），通过其标称值表示Qv和ω，泵扬程为

泵入口处的压力可由泵和吸入管道的联合操作确定，对于已定工况的管道泵，驱动液体流过管道所需的能量等于泵向液体施加的能量（Hpotr＝H）[14]：

由于扬程实际等于相同直径泵入口和出口处的压力差，参考式（13）可得出：

式中：Qv2为通过控制阀的流量，可表示为阀中的压降：

式中：kv为阀常数；函数A（Y）表示阀的横截面随主轴位置变化而变化的情况，此变化情况通常为非线性变化。

故离心泵的阻力扭矩为

将获得的各部分扭矩代入式（5）可得：

方程（18）定义了考虑设备的离心泵的非线性数学模型。

1.2 恒定液位水箱数学模型的建立

系统运行期间水箱中液位的动态变化由质量守恒原理决定。水箱中的质量变化等于水箱的输入质量减去水箱的输出质量，即：

式中：Qm为质量流率（Qm=ρQv）。

她立即瞥了两个黑斗篷一眼，还好，不像有人注意到。她赔出筹码，拿起茶杯来喝了一口，忽道：“该死我这记性！约了三点钟谈生意，会忘得干干净净。怎么办，易先生先替我打两圈，马上回来。”

假设流体密度ρ 随时间变化恒定（不可压缩流体），水箱为一横截面积为A 且横截面面积不随时间变化的棱柱形。以此假设情形，水箱中一定质量的液体m（t）对应水箱中特定流体高度hr（t）有：

式中：Qv2为经由式（16）确定的耦合变量；流体高度hr为经由式（20）确定的耦合变量。将此装置作为被控对象，地形吸力高度hgv是输出变量之一。由于hgv和hr之和为一定值h，hr的变化也能同时反应hgv在相反方向的变化，即：

消除式（20）中的耦合变量，可得装置内水箱的非线性数学模型：

2 离心泵输水系统的研究

MATLAB/Simulink 是机电一体化系统基于模型设计的领先的软件工具之一，也是控制系统开发和仿真工作的重要辅助工具。对实际系统的理论建模可以通过以下步骤完成：首先对实际系统进行简化，从而得到系统的物理模型；再根据系统的物理模型编写相关数学方程式，根据数学方程式可以形成实际系统的数学模型，数学模型可以用计算模型进行求解；最后通过仿真将计算结果可视化。

2.1 离心泵输水系统数学模型的建立

如图2 所示，该离心泵输水系统是一个带有流出阀的液体罐。模拟系统将计算并实时显示液体罐内的液面高度h。在实际情况时，液体罐液体流出速率较慢，在模拟系统中会对进程进行加速，以使模拟时间比实时运行得更快来避免不必要的时间浪费。由于模拟是实时的，会给人一种真实的感觉，用户可以通过调节泵控制信号u 来调节输入。每个模拟系统都基于需要模拟的系统的数学模型，因此应建立储液罐的数学模型。

图2 储液罐的物理模型Fig.2 Physical model of liquid storage tank

首先对实际系统进行简化。通过引入相关假设，可以简化实际系统，然后可以藉此构建相应的物理模型。现引入以下假设（以下表达式中使用的参数如图2 所示）：

（1）假设液体不可压缩，即液体的密度ρ 为常数；

（2）假设储液罐内壁垂直，即横截面积A 为常数；

（3）假设储液罐中液体质量和罐内液体高度的关系为

（4）假设泵进口体积流量与泵的控制信号成正比例关系，即：

（5）假设通过阀门出口的液体体积流量与阀门压降的平方根成正比，假设该压降等于储液罐底部的静水压力：

根据质量守恒定律，储液罐中液体的连续性方程可写为

代入以上假设中关系式得：

基于上述方程，可以绘制出该模型的数学框图，该框图可以在模拟框图中实现，作为绘制数学框图的起点，微分方程（27）可被写为以下形式：

以上方程（28）为储水罐内液面高度随时间变化的微分方程，即上述储水罐的数学模型。根据方程（28）对相对于从0 到t 时刻进行积分时，可通过模拟系统得到t 时刻储水罐内液面的高度。设储水罐内液面的初始高度为hinit，根据式（26）～（28）可得系统的最终框图如图3 所示。

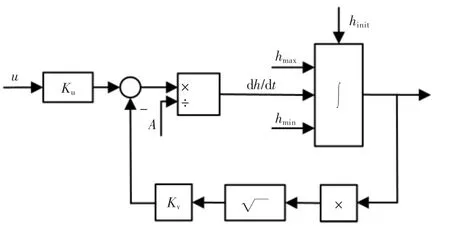
图3 储液罐的数学框图Fig.3 Mathematical block diagram of liquid storage tank

2.2 系统仿真

Simulink 提供了许多不同的基本运算模块，可以在Simulink 库浏览器中找到所需要的模块，点击加入到Simulink 窗口的位置，然后通过模块之间的接口进行连接，通过点击相应模块并输入相应的数字来对模块进行配置。在模拟的储液罐液位时，液位的初始值为0.5 m。离心泵的控制信号u 在20 s之前输入为0，在20 s 时电压变化为0～0.01 V。模拟从0 s 开始到50 s 内储液罐内液面的变化，其余各参数的数值如表1 所示。

表1 输水系统参数表Tab.1 Parameter of water transmission system

根据建立的Simulink 仿真模型，输入电机的控制信号如图4 所示。

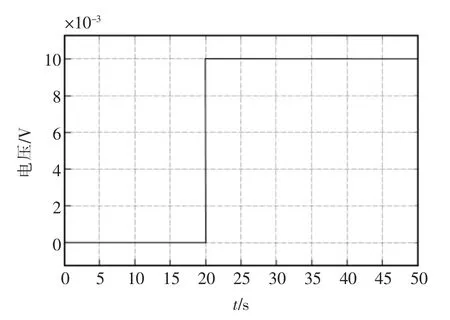
图4 离心泵控制信号图Fig.4 Control signal diagram of centrifugal pump

假设实际系统中存在一个液位传感器，在储水罐中液面过高或者过低时，会发出警报信号。设高点警报水位高度为hAH=0.9 m，低点警报水位高度为hAL=0.1 m，此两条警戒水位线应与储水罐内水位变化同时表示。根据以上数据，得到Simulink 仿真结果如图5 所示。由图可见，储水罐初始液面高度为0.5 m，在打开阀门20 s 后液面达到警戒水位以下，控制系统开始工作，储液罐中液面开始缓慢增加。控制结果证明了本文设计的离心泵输水系统的控制系统的有效性。

图5 储液罐内液位变化示意图Fig.5 Schematic diagram of liquid level changes in the storage tank

3 结语

离心泵系统的数学模型不仅从底层反应了实际系统的物理规则和运行模式，还为进一步研究离心泵系统如仿真和控制系统的建立提供了支撑。目前国内对离心泵系统的研究大多只限于运用有限元分析等软件工具对实际系统进行模拟，针对底层数学原理的研究较少，本文通过对离心泵系统的动态建模，分析并建立了典型离心泵系统的动态模型，对后续离心泵控制系统的设计和优化等工作具有相当重要的意义。此外，本文所设计的离心泵控制系统简单可靠、可适用性强，可广泛推广于其他领域的运用。