三维地质模型不确定性分析及对三维成矿预测结果的影响解析

秦 阳, 李晓晖*, 唐敏惠, 袁 峰, 张明明,李 贺, 薛 晨, 吴帮财

三维地质模型不确定性分析及对三维成矿预测结果的影响解析

秦 阳1, 2, 李晓晖1, 2*, 唐敏惠3, 袁 峰1, 2, 张明明1, 2,李 贺1, 2, 薛 晨1, 2, 吴帮财1, 2

(1. 合肥工业大学 资源与环境工程学院 合肥工业大学矿床成因与勘查技术研究中心(ODEC), 安徽 合肥 230009; 2. 安徽省矿产资源与矿山环境工程技术研究中心, 安徽 合肥 230009; 3. 安徽省公益性地质调查管理中心, 安徽 合肥 230091)

三维地质模型是三维成矿预测最重要的数据基础之一, 其准确性对于深部预测靶区的圈定具有十分重要的意义。然而, 三维地质模型存在一定程度的不确定性, 其不确定性主要是受到地质体与地质结构自身的复杂性, 数据密度、误差和建模方法等多方面影响。本文以长江中下游成矿带钟姑矿田为例, 基于隐式三维地质建模及蒙特卡洛模拟方法, 对控制剖面中地质界线产状引起的三维地质模型的不确定性开展定量分析, 并度量和评价其对三维成矿预测结果的影响。研究结果显示, 深部地质界线的产状倾角及倾向变化会导致三维地质模型产生不同程度的不确定性。通过扰动策略, 能够有效开展相关的不确定性分析和度量工作; 三维地质模型的不确定性会在一定程度上影响三维成矿预测结果, 但三维成矿预测方法具有一定的鲁棒性, 基于预测结果圈定的找矿靶区位置相对稳定。对于具有较高不确定性的深部预测靶区, 进一步工作可通过降低三维地质模型的不确定性或增加其他预测信息等方式, 提高预测结果的确定性, 以降低找矿勘探风险。

不确定性; 3D; 成矿预测; 隐式建模; 钟姑矿田

0 引 言

基于GIS的成矿预测是矿产勘探中寻找和圈定找矿靶区的有效方法, 以往研究主要是通过对多种二维地学信息进行集成来实现(Agterberg et al., 1990)。当前, 对于已有大量浅部勘查和找矿成果的成熟矿区, 寻找深部隐伏矿床是扩大矿区资源储备的重要途径, 也是近年来基于GIS成矿预测的重要研究目标之一。因此, 三维成矿预测方法被相继提出(毛先成等, 2009; Payne et al., 2015; Nielsen et al., 2015)。相较传统二维成矿预测方法, 三维成矿预测方法通过融合多源多维地学数据构建三维地质模型, 能够更好地对地质体的物理特性、空间特征进行刻画和分析(Murphy et al., 2006; Malehmir et al., 2009; Joly et al., 2012), 并通过开展三维空间分析和综合评价, 能更为充分地挖掘和综合多维地学信息中包含的控矿和指示要素信息, 预测和圈定三维找矿靶区。目前三维成矿预测方法已被广泛应用于成矿带、矿集区、矿田和矿床等多尺度深部找矿预测研究中, 为矿产勘查提供了新的方法和找矿目标(肖克炎等, 2012; Yuan et al., 2014; Li et al., 2015; Hu et al., 2020; Mao et al., 2020)。

成矿预测是一种基于多因子、多准则的综合方法, 其内含的数据和方法等具有很高的不确定性, 这种不确定性会影响预测结果, 提高找矿预测的风险。目前, 关于成矿预测的不确定性研究多集中于二维环境, 不确定性很大程度上与数据的质量有关(Carranza et al., 2005; Porwal et al., 2010; Lisitsin et al., 2014; Zuo et al., 2021)。对于融合更多数据和方法的三维成矿预测, 其不确定性更值得关注。三维地质模型作为三维成矿预测最主要的数据基础, 也是三维成矿预测最重要的环节(袁峰等, 2019), 对其不确定性研究具有十分重要的意义。

本文以长江中下游成矿带宁芜盆地的钟姑矿田为例, 基于蒙特卡洛模拟方法, 通过高斯分布生成控制剖面中地质界线产状数据的模拟数值; 利用三维隐式建模方法生成100个数据扰动后的三维地质模型, 以此对地质界线产状引起的三维地质模型的不确定性开展定量分析; 通过三维空间分析方法对扰动后的三维地质模型进行分析, 获取多套控矿要素信息, 并进一步开展数据融合与靶区圈定, 以度量和解析三维地质模型不确定性对三维成矿预测结果的影响。该研究可为进一步减少三维成矿预测结果的不确定性提出优化方案, 从而更好地提升三维成矿预测结果的可靠性, 降低深部找矿预测的风险。

1 数 据

长江中下游成矿带是中国东部重要的铜‒铁多金属成矿带(常印佛等, 1991), 发育宁芜、庐枞等多个火山岩盆地以及铜陵、鄂东南等多个矿集区。钟姑矿田位于长江中下游成矿带内宁芜盆地的南段, 矿田内地层主要为中三叠统周冲村组(T2)白云质灰岩夹膏盐层、上三叠统黄马青组(T3)砂页岩、上三叠统范家塘组(T3)砂页岩, 以及中下侏罗统象山群(J1-2)砂页岩(高道明和洪东良, 2008)。矿田内褶皱断裂构造发育, NNE向和NWW向两条基底断裂带控制了区内的火山‒侵入岩的发育以及矿化作用。火山岩主要发育于矿田西部和南部, 侵入岩主要发育于矿田中部及北部, 与铁矿有关的闪长岩类侵入体均为浅成‒超浅成的小岩体。矿田内发育大量热液矿床, 矿体主要产于闪长岩与三叠系膏岩层或含钙质地层的接触带部位, 具有明显的接触交代型铁矿床的地质特征。

本文用于三维地质建模和三维成矿预测的数据为钟姑矿田的基岩地质图和13条地质和地球物理综合解释剖面(图1), 通过蒙特卡洛模拟的方法, 扰动综合解译剖面中地质界线的产状, 利用隐式三维地质建模方法批量构建三维地质模型, 从而对三维地质模型的不确定性进行分析和度量。

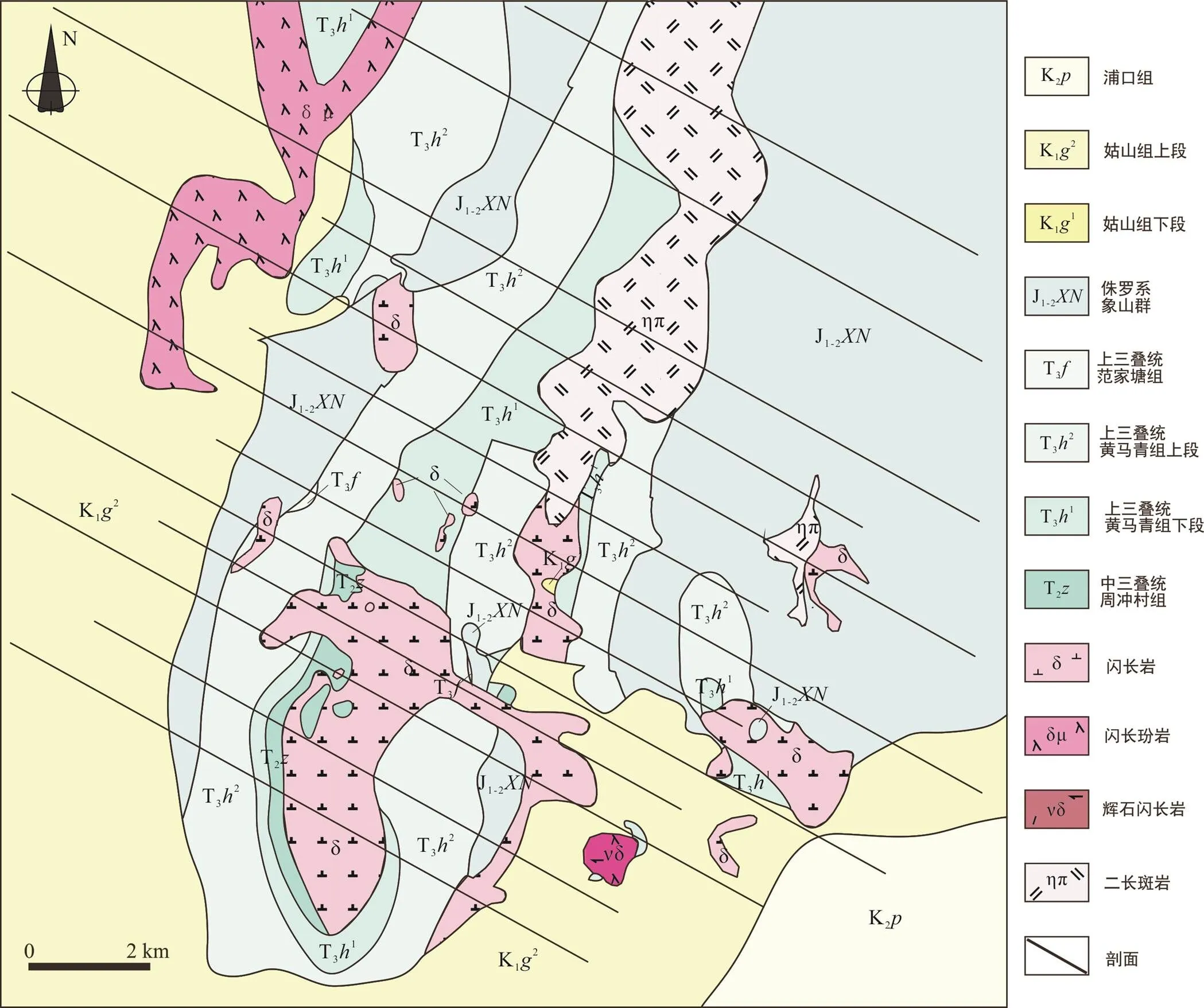
图1 矿田地质图及剖面位置(据Li et al., 2015修改)

2 研究方法

2.1 三维地质模型不确定性分析方法

随着深度的增加, 准确描述地质体和地质结构的难度不断加大。目前, 三维地质建模已成为描述地质体和地质结构的重要手段之一, 其主要采用隐式或显式的方法, 以有限的地质、地球物理平面和剖面数据以及钻孔数据作为约束, 对地质体和地质结构进行推演和模拟(Betts et al., 2003; Hills et al., 2003)。

三维隐式地质建模方法具有模型快速更新、多源数据融合、地质知识融入等优点, 近年来被广泛用于多尺度的三维地质建模研究工作(Wellmann et al., 2010; Caumon et al., 2013; Zhong et al., 2019)。三维隐式地质建模方法中最常采用协同克里格方法(公式1), 该方法能够充分融合位置和产状三维约束信息, 通过插值计算, 获取连续的三维势场标量函数, 进而更好、更合理地描述地质体的几何结构(Calcagno et al., 2008)。

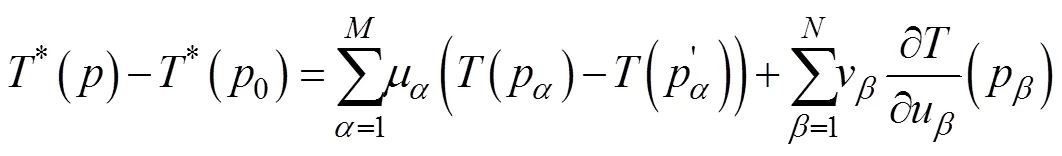
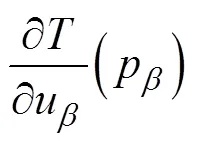
在三维地质建模中, 通常多会采用多条平行剖面描述和约束深部地质构造, 进而对整体地质结构进行模拟和推演。在这些平行剖面中, 地质界线的位置及产状主要通过地质和地球物理方法进行解释和描述; 对于平行剖面之间地质界线的形态和产状, 则主要通过人工连接或是基于上述插值方法计算获得。由于地表下地质界线是通过地球物理方式解译得到, 难免存在误差; 插值得到的结果也无法完全贴合实际的地质情况, 且平行剖面中的地质界线缺少垂直于剖面走向方向的产状信息约束。因此, 三维地质模型总是会存在一定的不确定性。其中, 不同的产状条件可能导致不同的建模结果。如图2所示, 在选取(a)作为两个剖面间的连接时, 在插值计算或手动连接时, 这两个剖面间的任意连接, 如(b)、(c), 可能是地质体的实际情况。

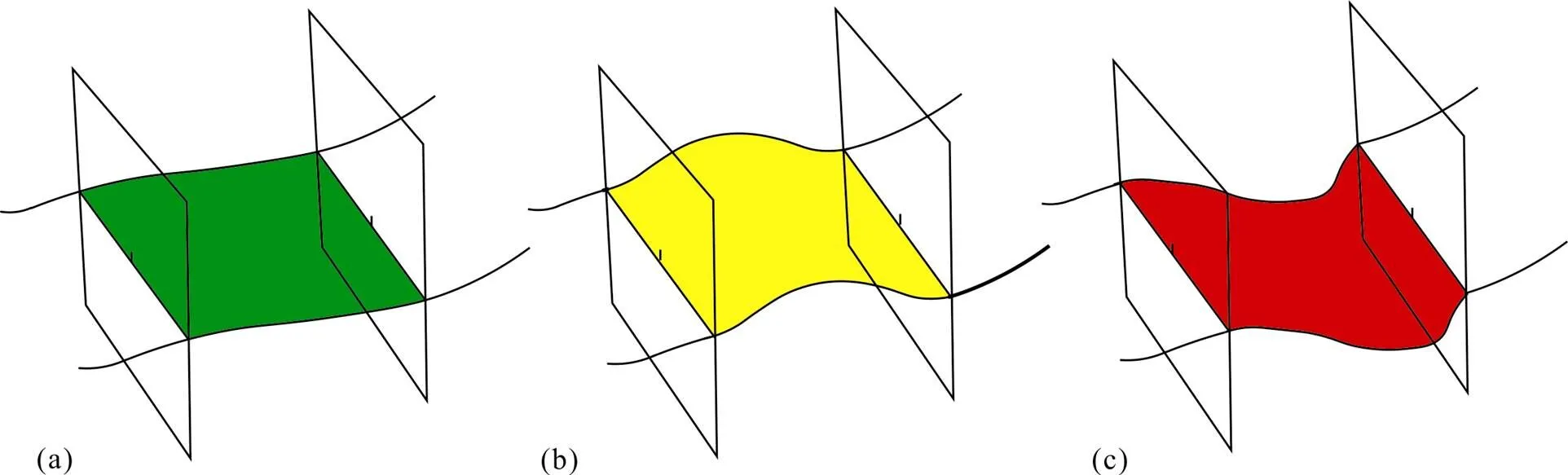
图2 地质解译与建模过程中的多解性

对于基于三维势场和协克里格插值方法的隐式三维地质建模方法, 倾角和倾向是度量地质体产状的主要参数, 特别是对于描述平行剖面间地质体和地质结构的三维形态时尤为重要。倾角主要影响地质界面的水平几何形态, 倾向主要影响地质界面的垂直几何形态(图3)。

(a) 水平向地质界线; (b) 水平向地质界线建立的原模型; (c) 倾向+10°建立的模型; (d) 倾角+10°建立的模型; (e) 竖直向地质界线; (f) 竖直向地质界线建立的原模型; (g) 倾向+10°建立的模型; (h) 倾角+10°建立的模型。

图3 地质界线中走向和倾角对三维地质模型的影响

Fig.3 The influences of the strike and dip of geological boundary on the 3D geological model

由于地质体存在多解性, 因此需要选择合适的方法对其进行模拟, 以构建出不同情况下地质体的三维地质模型结果。蒙特卡洛方法的基本思想是当所求解问题是某种随机事件出现的概率, 或者是某个随机变量的期望值时, 通过随机抽样的方法, 以随机事件出现的频率估计其自身的概率, 或者以抽样的数字特征估算随机变量的数学特征, 并将其作为问题的解, 主要步骤为: ①构造或描述概率过程; ②实现从已知概率分布抽样; ③建立各种估计量(朱陆陆, 2014)。该方法适用于不确定性过程的模拟。因此, 为了度量平行剖面中地质界线产状参数不确定性对三维地质模型的影响, 本文结合蒙特卡洛方法对平行剖面中地质界线的产状参数制定了随机扰动策略。方法和步骤如下:

(1) 设置参考模型, 假设剖面上地质界线的产状倾向垂直于剖面, 倾角垂直于地质界线, 通过基于三维势场插值的隐式三维地质建模方法, 构建三维地质模型(图4)。

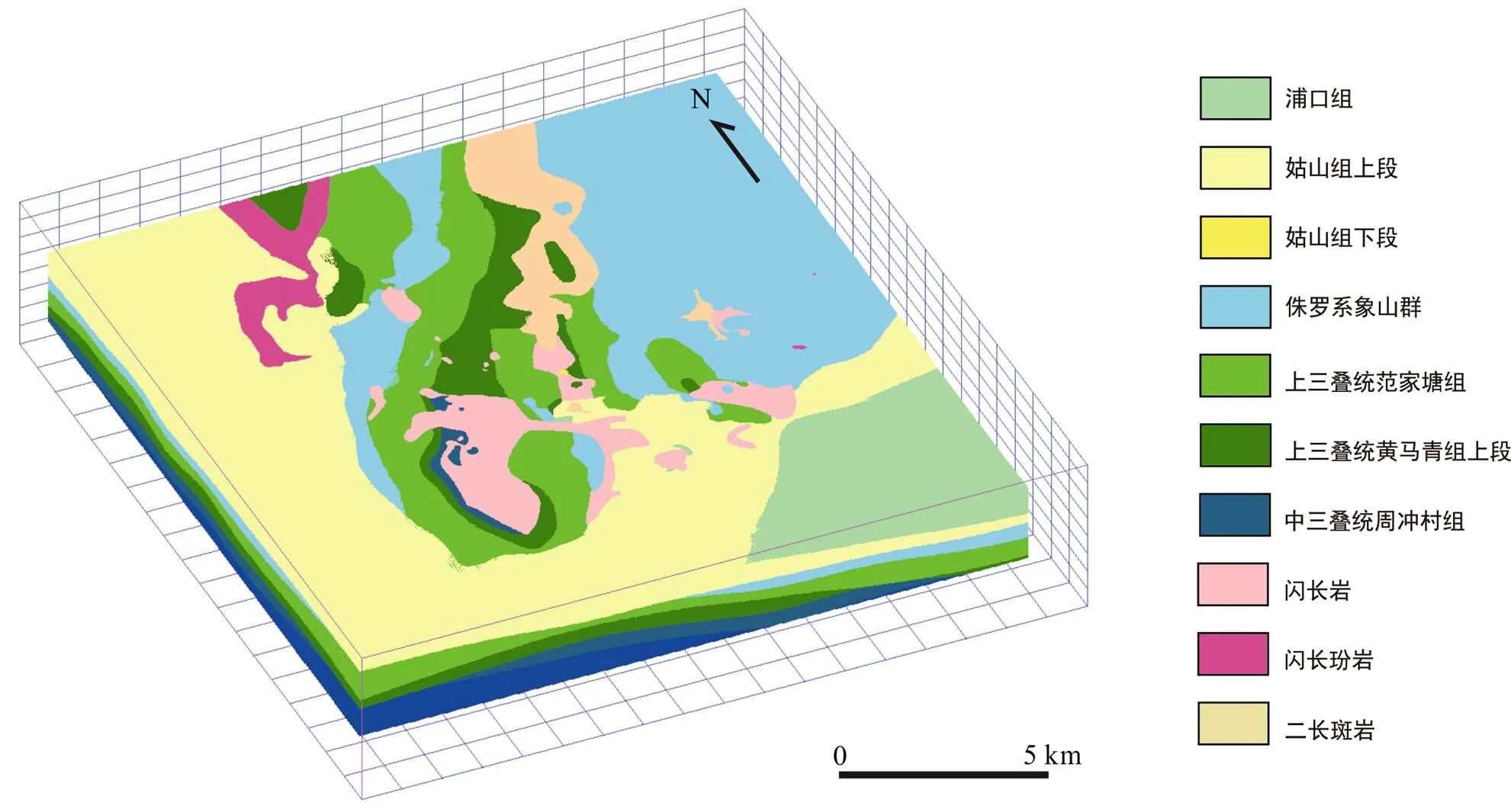
图4 参考模型结果及剖面位置(据Li et al., 2015修改)

(2) 在剖面上随机选取10%的地质界线产状中的倾角与倾向进行扰动。由于高斯分布符合大多数现象的概率分布(王浩龙, 2018), 因此, 将高斯分布作为先验概率分布来模拟原始数据点的不确定性(Pakyuz-Charrier et al., 2018)。高斯分布可定义为:

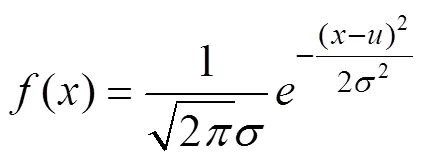
其中:和分别为均值和标准差。通过改变产状的倾角和倾向数据, 即由高斯分布随机生成的±度来扰动模型, 该度数是基于原始参考模型数据以高斯分布方法随机生成的。

(3) 依据上述方法产生100组扰动产状后的地质界线集合, 并用其重新计算和生成100个可能的地质模型。

(4) 将100个地质模型进行联合计算, 以分析和可视化不确定性。地质模型的不确定性可用值进行分析, 计算方法见Lindsay et al. (2012)。

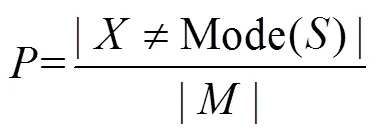
其中: Mode()代表在某位置出现最多的地层种类; |≠Mode()|是在该位置与Mode()不同的地层类别的数量; ||是总的模型数量。

2.2 三维成矿预测结果不确定性分析方法

三维成矿预测以三维地质模型为基础, 通过三维空间分析方法获取三维预测信息, 最后通过综合评价方法实现三维预测数据的融合与靶区圈定。本文从三维成矿预测全过程角度出发, 开展三维地质模型不确定性对三维成矿预测结果的影响的度量和分析研究, 不确定性分析方法和步骤如下:

(1) 由于三维成矿预测需要基于正六面体离散单元进行, 因此, 研究首先将上述101个地质模型(100个扰动模型和1个参考模型)分别离散为50 m× 50 m×50 m六面体单元。为了重点描述三维地质模型的不确定性对于三维成矿预测结果的影响, 本文选用的构建三维预测模型的预测要素均可采用三维空间分析方法基于三维地质模型计算得到(表1), 以排除三维地质模型以外其他来源相关的不确定性对三维成矿预测结果的影响。

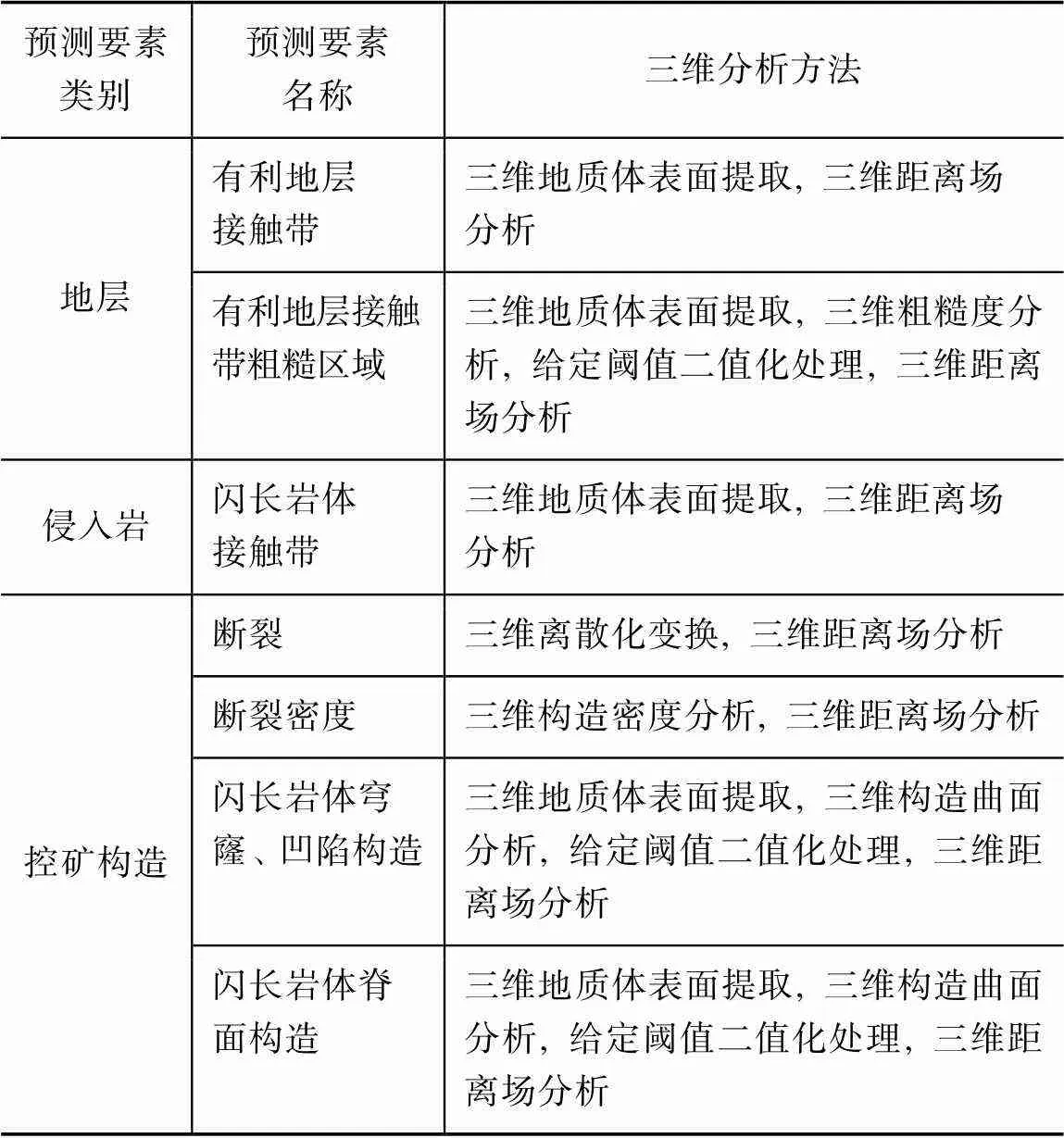
表1 成矿预测要素及三维空间分析方法

(2) 基于三维地质模型, 采用三维空间分析方法计算获取101组三维预测数据集, 最后采用数据驱动的逻辑回归模型, 分别对101组三维预测数据集进行综合, 计算成矿有利程度, 并根据阈值P=0.02(Li et al., 2015), 采用以下方式圈定深部找矿靶区(图5)。

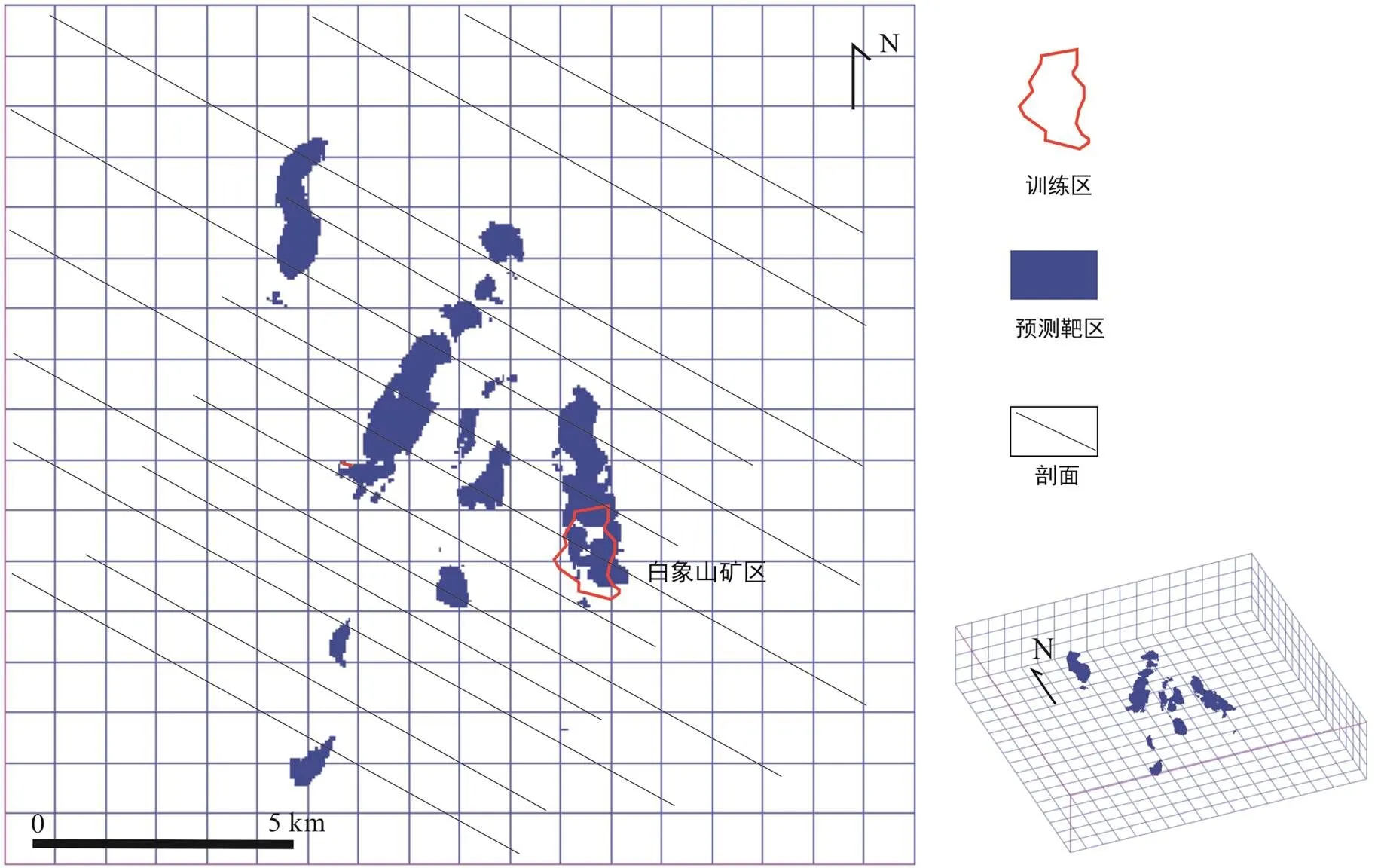
图5 参考模型三维成矿预测结果

其中:S为立方体单元是否在基于组预测数据集圈定的找矿靶区(成矿有利程度为≥P)内。

(3) 基于上述研究圈定的101组找矿靶区,即可使用N定量化度量三维地质模型对于三维成矿预测结果的不确定性影响:

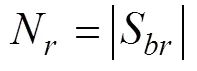
其中: |S|是立方体单元被圈定为找矿靶区的总次数。N值越小, 表示三维成矿预测结果的不确定性越高; 相反,N值越大, 表示三维成矿预测结果的不确定性越低。

3 结果与讨论

3.1 三维地质模型不确定性分析

通过扰动剖面内地质界线的产状数据来模拟分析三维地质模型的不确定性结果如图6所示。结果显示不确定性较高的区域主要集中在A、B和C区域中, 造成这些区域不确定性较高的主要原因是因为该区域内地质界线较为复杂, 曲率较高, 由于倾角和倾向对该区域影响的综合叠加, 使得区域的不确定性增加。

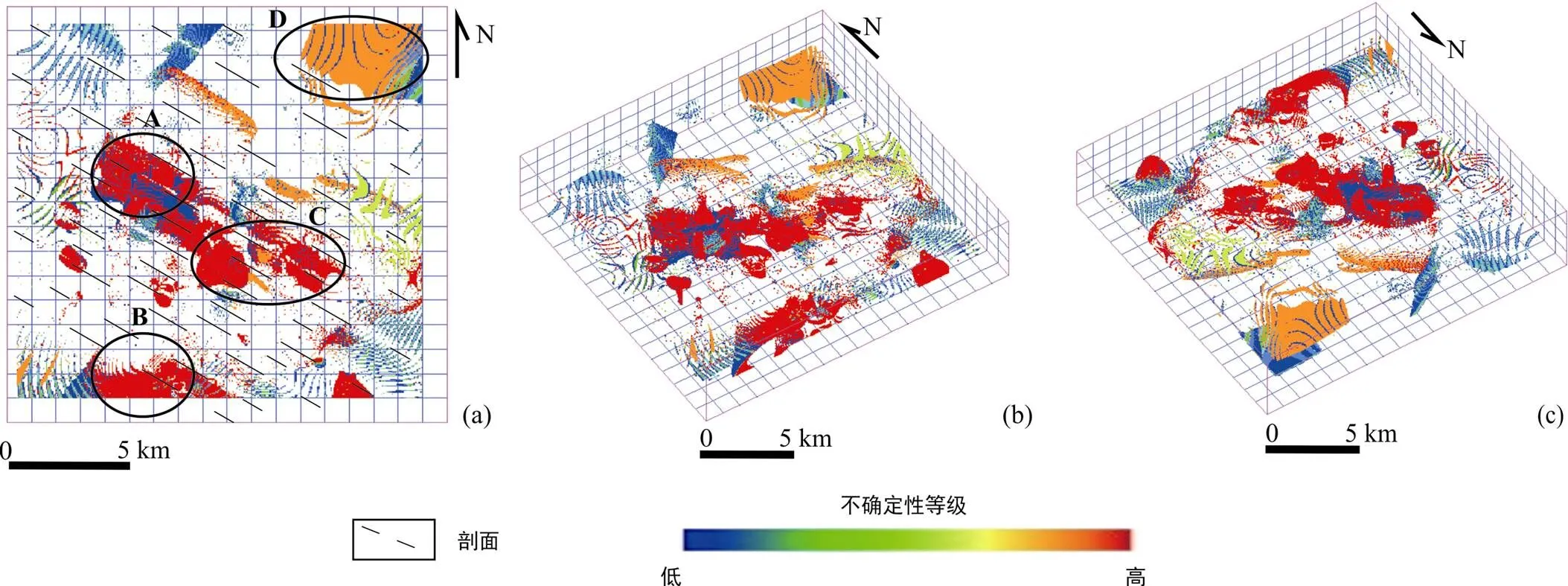
(a) 俯视图; (b) 西南方向侧视图; (c) 东北方向侧视图。

不确定性分析结果表明, 基于目前有限的平行剖面, 部分区域内的复杂地质体不能很好地描述, 具有较高的不确定性, 这些区域需要利用更为丰富的地质数据, 如垂直于平行剖面的剖面、钻孔数据, 或是对平行剖面进行加密, 以减小三维地质模型的不确定性。

3.2 三维成矿预测结果不确定性分析

基于101组三维地质模型计算得到的三维成矿预测结果的不确定性分析结果如图7所示。

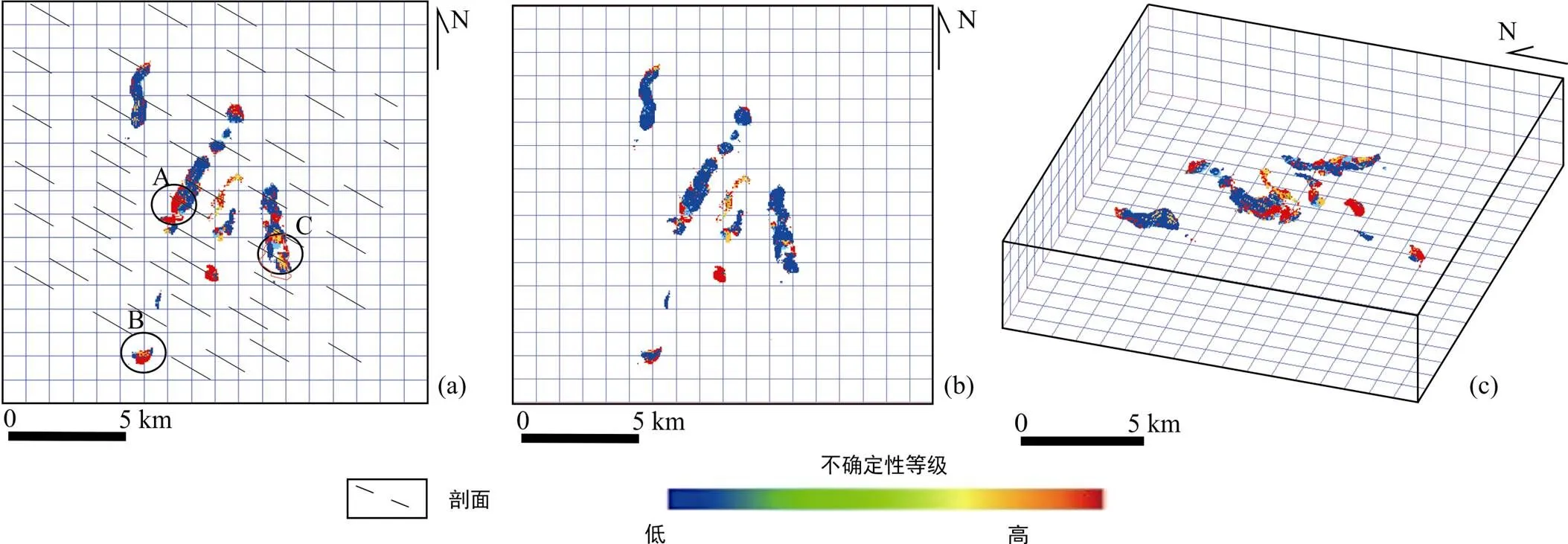
(a) 俯视图; (b) 仰视图; (c) 东北方向观察角度。

通过分析图6a和图7a可见, 三维成矿预测结果的不确定性与三维地质模型的不确定性在空间上存在一定的相关性。三维地质模型不确定性较高的地区主要集中在A区和B区, 上述两处区域中三维成矿预测结果的不确定性也相对较高。由此可见, 三维地质模型的不确定性会经过三维空间分析、三维综合评价等过程传递, 最终增加三维成矿预测结果的不确定性。因此要降低该位置的三维成矿预测结果的不确定性, 可通过增加穿越该位置的地质、地球物理综合解译剖面、钻孔方式降低三维地质模型的不确定性, 或是添加其他三维预测要素等方式进行改善。

但三维成矿预测结果的不确定性与三维地质模型的不确定性有时也存在着一定的差异性。三维地质模型的四周(图6a中的区域D)虽然其不确定性较高, 但由于其有利的成矿条件, 因此并不会影响三维成矿预测结果, 对于靶区圈定几乎没有影响。因此, 对于这些区域, 虽然三维地质模型的不确定性程度较高, 但对于三维成矿预测研究, 可以不去优化和降低模型的不确定性; 有限的精力和资源应当集中于三维成矿预测结果中具有较高不确定性区域的三维地质模型的优化, 以增强其确定性, 这也是开展不确定性分析和度量的重要目的之一。此外, 成矿预测结果(图7b、c)还显示, 部分三维成矿预测结果中具有较高不确定性的单元, 都位于较低不确定性单元的周围, 尤其是深部和浅部, 显示出地质界线的埋深对于三维成矿预测的结果具有较大的影响。在实际找矿勘查工作中, 目标靶区的最浅埋深应当以不确定性分析后, 通过统计具有较低不确定性的单元获得, 以避免由于不确定性导致的勘探深度不足等问题。

结合图5和图7a还可以看出三维成矿预测方法具有一定的鲁棒性, 具体表现为: ①尽管101个三维地质模型由于数据扰动后, 其内部地质结构各不相同, 导致三维空间分析后生成的预测要素也有所不同, 但经过对预测要素进行综合预测后得到三维成矿预测结果显示, 基于扰动数据预测的成矿靶区位置与参考模型在空间上没有明显变化, 埋深及厚度上也较为一致, 显示出预测结果的不确定性较小。②分析结果中,N<10的立方体单元仅占总体预测结果单元约1%,N<90的立方体单元仅占总体预测结果单元约16%(图8), 表明预测结果总体的不确定性程度较低; 同时, 靶区内部不确定性程度较低, 几乎没有出现具有较高不确定性的立方体单元, 较高不确定性单元多分布于少数靶区的外围空间。

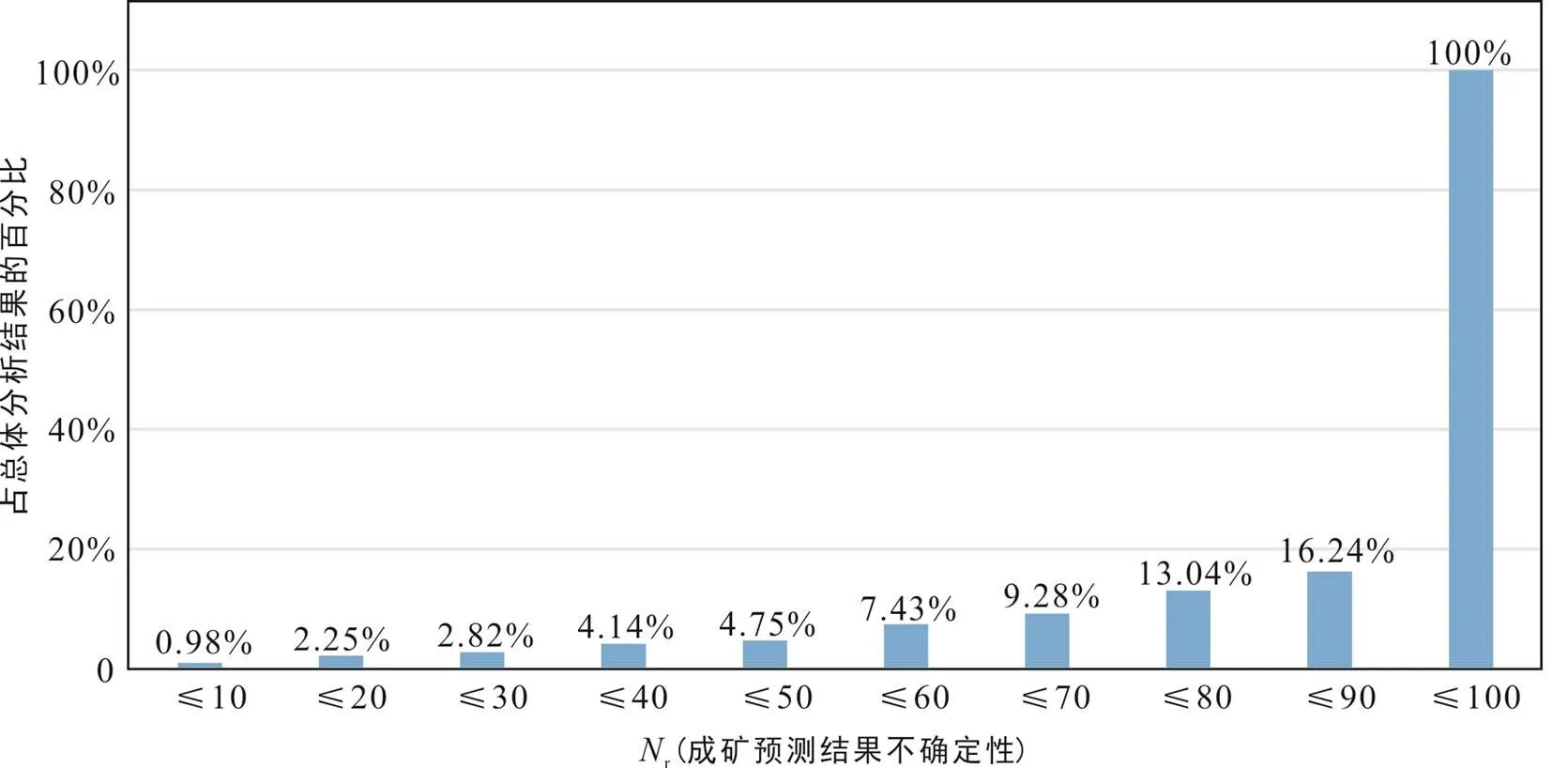
图8 Nr(成矿预测结果不确定性)累积直方图

综上, 通过不确定性分析, 开展补充工作可以进一步优化三维地质模型和三维成矿预测成果; 进一步的找矿勘查工作也能够基于不确定性分析结果, 更加合理的规划实施方法。对于具有较低不确定性的预测靶区可以先期开展找矿勘查, 对于具有较高不确定性的预测靶区, 需要视其成矿潜力投入更多的地质工作, 以进一步降低找矿勘查风险。

4 结 论

(1) 三维隐式地质建模过程中, 在地质界线位置信息不变的情况下, 产状信息变化会导致地质模型产生不同程度的不确定性。通过扰动策略, 能够较好地评价受上述因素导致的不确定性, 进而提示哪些空间位置需要开展进一步的研究工作, 以降低模型的不确定性。

(2) 基于扰动的三维地质模型, 通过联动三维空间分析方法和综合评价方法能够有效分析和度量三维地质模型对三维成矿预测结果的不确定性影响程度。三维地质模型的不确定性一定程度会影响三维成矿预测结果, 两者既有相关性又存在差异性。虽然三维地质模型的不确定性会对预测靶区外部产生一定的影响, 但三维成矿预测结果圈定的找矿靶区空间位置相对稳定、不确定性高的单元数量较少、靶区内部不确定性程度较低, 表明三维成矿预测方法具有一定的鲁棒性。

(3) 对于具有较高不确定性的深部预测靶区, 可通过进一步工作降低三维地质模型的不确定性或增加三维地质模型外的预测信息等方式, 提高预测结果的确定性, 降低找矿勘探风险。进一步勘探工作的实施顺序可以基于三维预测结果的不确定性和成矿有利程度进行综合分析。

致谢: 课题组的师兄师姐在论文撰写过程中提供了帮助与指导, 两位匿名审稿人提出了建设性的修改意见, 在此一并致以诚挚的感谢。

常印佛, 刘湘培, 吴言昌. 1991. 长江中下游铜铁成矿带. 北京: 地质出版社: 1–370.

高道明, 洪东良. 2008. 钟姑矿田铁矿成矿模式与规律及找矿标志. 金属矿山, (7): 84–87.

毛先成, 戴塔根, 吴湘滨, 邹艳红. 2009. 危机矿山深边部隐伏矿体立体定量预测研究——以广西大厂锡多金属矿床为例. 中国地质, 36(2): 424–435.

王浩龙. 2018. 复杂地质构造不确定性可视化及分析方法研究. 成都: 电子科技大学硕士学位论文: 1–76.

肖克炎, 李楠, 孙莉, 邹伟, 李莹. 2012. 基于三维信息技术大比例尺三维立体矿产预测方法及途径. 地质学刊, 36(3): 229–236.

袁峰, 张明明, 李晓晖, 葛粲, 陆三明, 李建设, 周宇章, 兰学毅. 2019. 成矿预测: 从二维到三维. 岩石学报, 35(12): 3863–3874.

朱陆陆. 2014. 蒙特卡洛方法及应用. 武汉: 华中师范大学硕士学位论文: 1–56.

Agterberg F P, Bonham-Carter G F, Wright D F. 1990. Statistical pattern integration for mineral exploration // Gaal G, Merriam D F. Computer Applications in Resource Estimation. Oxford: Pergamon Press: 1–21.

Betts P G, Valenta R K, Finlay J. 2003. Evolution of the Mount Woods Inlier, northern Gawler Craton, Southern Australia: An integrated structural and aeromagnetic analysis., 366(1): 83–111.

Calcagno P, Chilès J P, Courrioux G, Guillen A. 2008. Geological modelling from field data and geological knowledge: Part Ⅰ. Modelling method coupling 3D potential-field interpolation and geological rules., 171(1): 147–157.

Carranza E J M, Woldai T, Chikambwe E M. 2005. Application of data-driven evidential belief functions to prospectivity mapping for aquamarine-bearing pegmatites, Lundazi District, Zambia., 14(1): 47–63.

Caumon G, Gray G, Antoine C, Titeux M O. 2013. Three- dimensional implicit stratigraphic model building from remote sensing data on tetrahedral meshes: Theory and application to a regional model of La Popa Basin, NE Mexico., 51(3): 1613–1621

Hills Q G, Betts P G, Lister G S. 2003. Geophysical interpretationand modelling of the Olary Domain under cover: A hiddeninverted rift system., 50(4): 633–644.

Hu X Y, Li X H, Yuan F, Ord A, Jowitt S M, Li Y, Dai W Q, Zhou T F. 2020. Numerical modeling of ore-forming processes within the Chating Cu-Au porphyry-type deposit, China: Implications for the longevity of hydrothermal systems and potential uses in mineral exploration., 116, 103230.

Joly A, Porwal A, McCuaig T C. 2012. Exploration targeting for orogenic gold deposits in the Granites-Tanami Orogen: Mineral system analysis, targeting model and prospectivity analysis., 48: 349–383.

Li X H, Yuan F, Zhang M M, Jia C, Jowitt S M, Ord A, Zheng T K, Hu X Y, Li Y. 2015. Three-dimensional mineral prospectivity modeling for targeting of concealed mineralization within the Zhonggu iron orefield, Ningwu Basin, China., 71: 633–654.

Lindsay M D, Aillères L, Jessell M W, de Kemp E A, Betts P G. 2012. Locating and quantifying geological uncertainty in three-dimensional models: Analysis of the Gippsland Basin, southeastern Australia., 546–547(11): 10–27.

Lisitsin V A, Porwal A, Mccuaig T C. 2014. Probabilistic fuzzy logic modeling: Quantifying uncertainty of mineral prospectivity models using Monte Carlo simulations., 46(6): 747–769.

Malehmir A, Thunehed H, Tryggvason A. 2009. The Paleoproterozoic Kristineberg mining area, northern Sweden: Results from integrated 3D geophysical and geologic modeling, and implications for targeting ore deposits., 74(1): 9–22.

Mao X C, Zhang W, Liu Z K, Ren J, Bayless R C, Deng H. 2020. 3D Mineral prospectivity modeling for the low-sulfidation epithermal gold deposit: A case study of the Axi gold deposit, Western Tianshan, NW China., 10(3): 233–233.

Murphy F, Rawling T, Wilson C, Dugdale L, Miller J M. 2006. 3D structural modelling and implications for targetinggold mineralization in western Victoria., 53(5): 875–889.

Nielsen S H, Cunningham F, Hay R, Partington G, Stokes M. 2015. 3D prospectivity modelling of orogenic gold in the Marymia Inlier, Western Australia., 71: 578–591.

Pakyuz-Charrier E, Lindsay M, Ogarko V, Giraud J, Jessell M. 2018. Monte Carlo simulation for uncertainty estimation on structural data in implicit 3-D geological modeling, a guide for disturbance distribution selection and parameterization., 9(2): 385–402.

Payne C E, Cunningham F, Peters K J, Nielsen S, Puccioni E, Wildman C, Partington G A. 2015. From 2D to 3D: Prospectivity modelling in the Taupo volcanic zone, New Zealand., 71: 558–577.

Porwal A K, Kreuzer O P. 2010. Introduction to the special issue: Mineral prospectivity analysis and quantitative resource estimation., 38(3): 121–127.

Wellmann J F, Horowitz F G, Schill E, Regenauer-Lieb K. 2010. Towards incorporating uncertainty of structural data in 3D geological inversion., 490(3): 141–151.

Yuan F, Li X H, Zhang M M, Jowitt S M, Jia C, Zheng T K, Zhou T F. 2014. Three-dimensional weights of evidence- based prospectivity modelling: A case study of the Baixiangshan mining area, Ningwu Basin, Middle and Lower Yangtze Metallogenic Belt, China., 145: 82–97.

Zhong D Y, Wang L G, Bi L, Jia M T. 2019. Implicit modeling of complex orebody with constraints of geological rules., 29(11): 2392–2399.

Zuo R G, Kreuzer O P, Wang J, Xiong Y H, Zhang Z J, Wang Z Y. 2021. Uncertainties in GIS-based mineral prospectivity mapping: Key types, potential impacts and possible Solutions., 30(5): 3059–3079.

Uncertainty of 3D Geological Modeling and its Influence on 3D Mineral Prospectivity

QIN Yang1, 2, LI Xiaohui1, 2*, TANG Minhui3, YUAN Feng1, 2, ZHANG Mingming1, 2, LI He1, 2, XUE Chen1, 2, WU Bangcai1, 2

(1. Ore Deposit and Exploration Centre (ODEC), School of Resources and Environmental Engineering, Hefei Universityof Technology, Hefei 230009, Anhui, China; 2. Anhui Province Engineering Research Center for Mineral Resources and Mine Environments, Hefei 230009, Anhui, China; 3. Public Geological Survey Management Center of Anhui Province, Hefei 230091, Anhui, China)

Three-dimensional (3D) mineral prospectivity delineates the target mining area based on 3D geological model. The 3D geological model is the foundation of 3D mineral prospectivity. Due to the complexity and diversity of geology itself, data errors, modeling methods, and other factors, 3D geological model is bound to have uncertainty that will directly affect the target area of 3D mineral prospectivity. The Zhonggu iron orefield located in the middle and lower Yangtze metallogenic belt of Eastern China is taken as an example to research the influence of the uncertainty of the 3D geological model on 3D mineral prospectivity. Based on the implicit modeling method and Monte Carlo simulation method, a set of geological models are generated by randomly disturbing the strike and dip direction of the geological boundary. By using the 3D spatial analysis method and logistic regression method, the prospecting target area is prospected through the relevant ore-controlling and indicator elements, and analyzing the influence of the uncertainty of the 3D geological model. Research shows that the change of the strike and dip direction will influence 3D geological model and the results of 3D mineral prospectivity. The disturbance strategy described in this paper can effectively analyze and measure the uncertainty. The uncertainty of 3D geological model will affect the results of 3D mineral prospectivity. At the same time, the 3D mineral prospectivity method has certain robustness, and the 3D prediction results are relatively stable in delineating the prospecting target area. To reduce the uncertainty of the 3D mineral prospectivity and reduce the risk of prospecting and exploration, further work should be done to reduce the uncertainty of the 3D geological model or increase the ore-controlling and indicator elements in the 3D spatial analysis.

uncertainty; 3D; mineral prospectivity modeling; implicit modeling; Zhonggu orefield

2021-11-01;

2022-03-09

国家自然科学基金项目(41702353、42072321)和中央高校基本科研业务费专项资金(PA2019GDZC0093)联合资助。

秦阳(1997–), 男, 硕士研究生, 地理学专业。E-mail: 951051510@qq.com

李晓晖(1986–), 男, 副教授, 主要从事数学地质与三维GIS方面研究工作。E-mail: lxhlixiaohui@163.com

P612

A

1001-1552(2023)05-1173-010

10.16539/j.ddgzyckx.2023.05.013