陆海交界区与运动目标复合散射的矩量法研究

于少帅,任新成,杨天赐,赵 晔,杨鹏举

(延安大学 物理与电子信息学院,陕西 延安 716000)

0 引言

地、海背景与运动目标的复合电磁散射特性在民事、军事方面均有重要的应用价值,可为遥感、无线通信等民事应用,目标雷达成像、识别、检测、分类等军事应用提供一定的理论依据[1-4]。地球表面由71%的海洋和29%的陆地组成,我国主张管辖的海域面积大小约为300万平方公里,其中包括内海、领海、毗连区、专属经济区和大陆架,其中不乏较大的陆海交界区域,因此,研究陆海交界区域的电磁散射特性具有重要的意义。

在之前的研究中,张童[5]使用时域有限差分方法研究了有限深度海域海面的电磁散射特性,谭秋意[6]使用近似解析方法对有限深海域的电磁散射特性进行了系统性的研究,董子宇[7]使用时域有限差分法研究了沥青混凝土地面的电磁散射特性,Behdani Mahdi[8]使用物理光学方法研究了海面与二维船体目标的复合电磁散射,WANG等[9]采用混合算法研究了粗糙面与其上方目标的复合散射特性,王安琪[10]采用矩量法研究了一维理想导体粗糙面与上方二维目标的复合电磁散射特性,邹高翔等[11-12]提出了一种基于分区域面元的迭代物理光学法,计算了陆海交界区复合粗糙面的电磁散射特性。以上目标与环境电磁散射特性的研究中,目标都是静止的,在任何方向上都不会发生运动,不仅如此,目标所处的环境大部分是地面或海面的其中一个。

实际上,自然界中目标除处在单纯的地面、海面背景中之外,有的还处于陆海交界区域附近,且目标有时是运动的,因此,研究陆海交界区域表面与上方运动目标复合散射特性具有与研究地面、海面与上方运动目标复合散射特性同样重要的意义。

本文通过Monte Carlo方法生成功率谱密度分别为PM海谱、TMA海谱和指数功率谱的深水海域海面、有限深海域海面[13-14]与海岸地貌表面,并参照国际无线电咨询委员会[15]推荐的一套介质反射系数图表分别模拟海水与海岸的介电常数,对于陆海交界区域表面上方圆形截面柱在不同方向上的运动进行建模,应用矩量法[16]计算了海岸地貌表面上方、有限深海域海面上方以及深水海域表面上方圆形截面柱在纵向平移与横向平移两种移动方式下的复合电磁散射特性,并分析了目标分别移动至海岸地貌表面、有限深海域海面、深水海域海面三种背景上方对复合散射系数造成的影响,所得结果可为一系列军用、民用领域问题提供理论支撑。

1 复合电磁散射建模

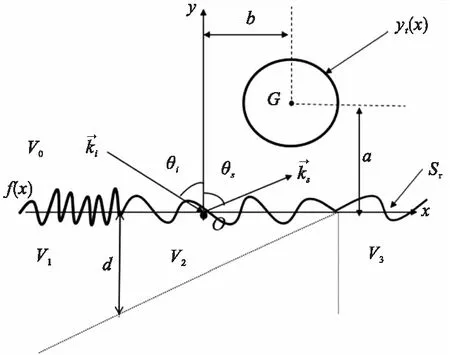
图1 陆海交界区域表面与上方运动目标复合散射几何示意图

本文使用Monte Carlo方法[17]分别模拟生成一维海面与一维海岸地貌表面进行分析讨论,根据Monte Carlo方法,在得出粗糙面功率谱后可由以下函数生成长度为L的一维粗糙面如式(1)所列。

(1)

式(1)中xn=nΔx(n=-N/2,...,N/2)为粗糙面的第n个采样点,F(kj)为滤波后所得到的粗糙面频谱,f(xn)为F(kj)的傅里叶变换对。表达式如式(2)所列。

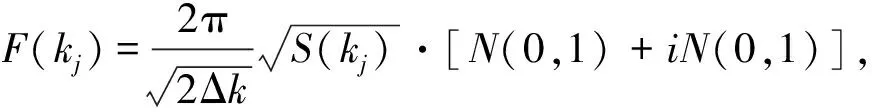
j=-N/2+1,…,-1

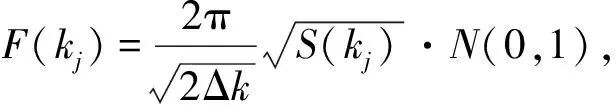
j=0,N/2

(2)

式(2)中,kj=2πj/L,Δk为谱域相邻的谐波样本的空间波束差;S(kj)为粗糙面的功率谱密度,N(0,1)表示均值为0,方差为1的正态分布随机数。

1.1 深水海域海面建模

海面功率谱定义为海面高度相关函数的傅里叶变换,PM海谱模拟传统的海域海面比较具有代表性并得到了广泛的应用,因此本文在模拟深水海域海面时,也采用传统的PM海谱进行模拟,传统的PM海谱[17]表达式如式(3)所列。

(3)

式(3)中,α和β是无量纲经验常数,α=8.10×10-3,β=0.74;gc是重力加速度,为9.81 m/s2;U19.5是海面19.5 m高度处的风速。值得注意的是,在模拟一维海面时,需将式(1)改写为如式(4)、式(5)所列。

(4)

其中,

ω(kj)={gc|kj|[1+(kj/363.2)2]}1/2eikjxn

(5)

1.2 有限深海域海面建模

本文在模拟有限深海域海面时,考虑到PM海谱为描述深海海面的全向海谱,因此选用引入了变浅系数的TMA海谱[13-14]来模拟有限深度海面[18],该海谱模拟生成的海面为有限深度海面,与真实海域背景中的近岸海面情形更为相近。在PM谱的基础上引入修正因子f可得到非稳态海谱JONSWAP谱[19],该海谱被认为是国际标准海谱,如式(6)所列。

Sj(k)=S(k)·f

(6)

式(6)中,S(k)为PM海谱,f为修正因子[11-12],在模拟近岸海面时,令α=10×10-3,此时该海谱为非充分发展JONSWAP谱,并引入变浅系数ξ与JONSWAP谱相结合,即可得到TMA海谱,如式(7)所列。

St(k)=Sj(k)·ξ2

(7)

式(7)中,Sj(k)为JONSWAP谱,变浅系数[11]ξ定义为水域有限深度d所对应的波高与无限水深所对应的波高的比值,如式(8)所列。

(8)

1.3 海岸地貌表面建模

常用的粗糙面功率谱密度有高斯功率谱密度、指数功率谱密度等,一般在模拟土壤粗糙面时选用指数功率谱,该功率谱表达式比较简单,能更好的体现电性参数以及其他因素对散射系数的影响,因此本文在建模海岸地貌表面时也选用指数功率谱[17]来进行模拟,如式(9)所列。

(9)

式(9)中,δ和l分别表示粗糙面的均方根高度和相关长度,得到指数功率谱密度之后,利用式(1)、(2)即可模拟生成一维指数随机粗糙面。

1.4 介电常数

本文参照国际无线电咨询委员会推荐的一套介质反射系数图表[15],选取不同介质的复介电常数进行仿真,如表1所列。

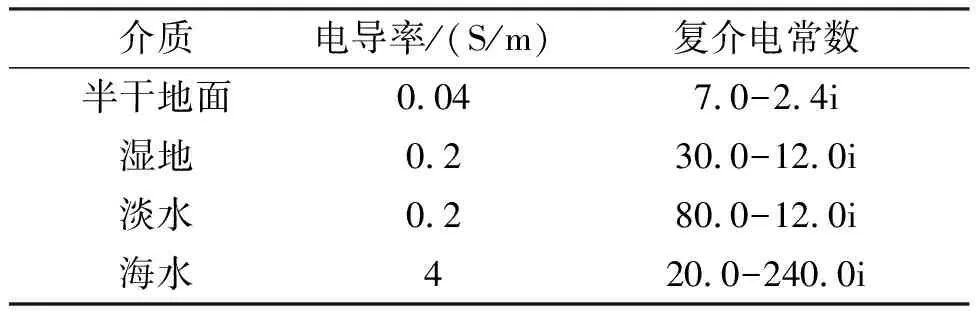
表1 不同介质粗糙面的复介电常数

根据表1分别选取海岸地貌表面介电常数为εs1=7.0-2.4i,选取海水介电常数为εs2=20.0-240i。

2 矩量法理论

当圆形截面柱目标位于V0区域即自由空间内时,研究该目标与粗糙面复合散射不仅需要考虑目标与粗糙面各自的散射特性,还要考虑两者的耦合,此时,可得到积分方程,如式(10)所列。

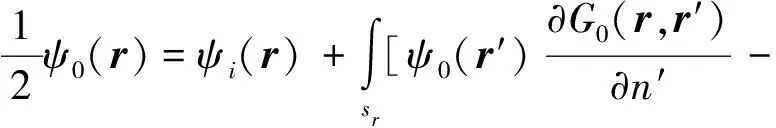
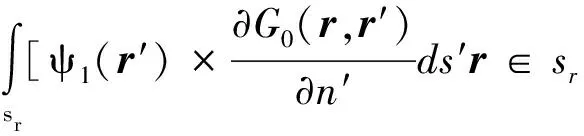
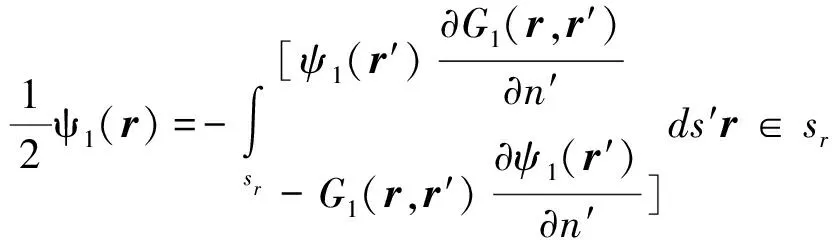
(10)

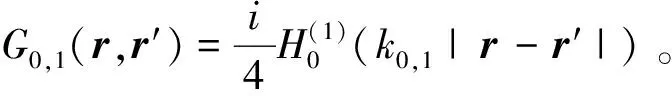
对于粗糙面sr上任意点r(即r∈sr),ψ0(r)和ψ1(r)满足边界条件,如式(11)所列。

(11)

式(11)中,ρ=ε1/ε0,ε1表示下方空间(即V1、V2、V3)中介质的介电常数,ε0表示上方空间V0中空气的介电常数。

将粗糙面sr沿x方向离散,将目标沿其表面轮廓so离散,利用矩量法将式(10)的积分方程离散化为下面的矩阵方程,如式(12)所列。

(12)

引入锥形波[20]作为入射波,此时粗糙面与目标的复合散射系数如式(13)所列。

(13)

在计算过程中,取归一化复合散射系数[16]为:σ=log10σ(θs)。其中,

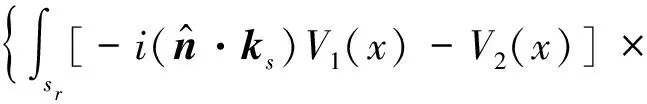
(14)

本文中的复合散射系数通过对粗糙面进行归一化计算得出。

3 数值仿真结果与分析

3.1 算法验证

为了验证矩量法(method of moments,MoM)算法的正确性,令入射波频率为1 GHz,入射角θi=30°,海岸介电常数εs1=7.0-2.4i,上方运动圆形截面柱目标半径为2.0λ、其重心G到x轴的距离a=2.0λ、到y轴的距离b=0.0λ,分别使用MoM与时域有限差分法(finite-difference time-domain,FDTD)[21]对粗糙面及其上方圆形截面柱的复合散射系数进行计算,计算结果如图2所示。

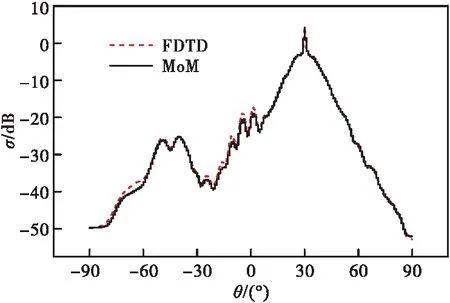
图2 FDTD与MoM算法结果对比

从图2可以看出,两种算法所得出的角分布曲线非常接近,这就验证了MoM算法的正确性。

3.2 海岸地貌表面

若无特殊说明,在海岸地貌表面情形下,取入射波频率均为1 GHz,入射角θi=30°;海岸介电常数εs1=7.0-2.4i,上方运动圆形截面柱目标半径为2.0λ、其重心G到x轴的距离a=2.0λ、到y轴的距离b=0.0λ,海岸地貌表面采样点1 024个,采样间隔为0.1λ,仿真统计个数100个。

3.2.1 纵向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到x轴的距离分别为a=2.0λ、a=30.0λ、a=60.0λ,分析目标纵向平移的距离a对复合散射系数σ的影响,计算结果如图3所示。

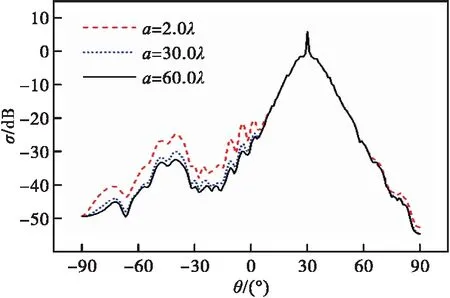
图3 海岸地貌表面上方目标纵向平移对散射系数的影响

由图3可以看出,目标的纵向平移距离a对复合散射系数σ有着比较规律的影响,除0°<θs<60°时,复合散射系数σ几乎不随目标纵向平移距离a的变化而变化,在其他散射角变化的范围内均有a越大,σ越小的结论。这是由于海岸地貌表面上方目标在竖直方向向上平移的过程中,距离地面越远,目标与地面之间的耦合效应越弱,从而整个模型的复合散射系数越小。

3.2.2 横向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到y轴的距离b=0.0λ、b=20.0λ、b=40.0λ,研究目标横向平移的距离b对散射系数σ的影响,计算数值结果如图4所示。

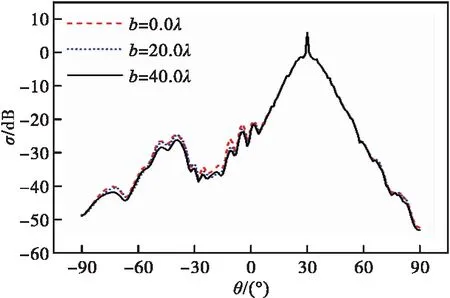
图4 海岸地貌表面上方目标横向平移对散射系数的影响

从图4可以看出,海岸地貌表面上方目标仅在水平方向进行平移时,复合散射系数σ所受到的影响较小。尤其是在镜反射方向附近的范围,σ几乎没有发生任何变化。b=0.0λ时的σ始终是最大的,但与b取其他两种情形(即b=20.0λ和b=40.0λ)时的σ差距也并不大。总体来讲,目标的横向平移距离b会对复合散射系数σ造成一定影响,但由于横向平移对目标与粗糙面的耦合产生的影响较小,所以对符合散射系数造成的影响也较小。

3.3 有限深海域海面

若无特殊说明,在有限深海域海面情形下,取入射波频率均为1 GHz,入射角θi=30°,海水介电常数εs2=20.0-240i,海水表面风速取U19.5=5 m/s;海面上方圆形截面柱目标半径为2.0λ、其重心G到x轴的距离a=2.0λ、到y轴的距离b=0.0λ,有限深海域海面采样点1 024个,采样间隔为0.1λ,仿真统计个数100个。

3.3.1 纵向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到x轴的距离分别为a=2.0λ、a=30.0λ、a=60.0λ,分析讨论目标纵向平移的距离a对复合散射系数σ的影响,计算结果如图5所示。

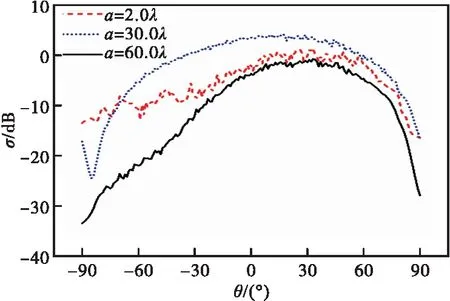
图5 有限深海域海面上方目标纵向平移对散射系数的影响

从图5可以看出,目标的纵向平移距离a对复合散射系数σ的影响比较显著,除θs<-60°时,a=2.0λ时的复合散射系数σ最大,在其余散射角θs变化的范围内,均有a=30.0λ时的σ最大,a=2.0λ的σ次之,而在所有散射角变化的范围(即-90°<θs<90°)内a=60.0λ时的σ均为最小,这是由于海面对电磁波的吸收能力较强,因此目标在有限深海域海面上方纵向移动的距离a会对目标与海水之间的耦合效应产生影响,从而对复合散射系数σ造成较为可观但比较复杂的影响。

3.3.2 横向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到y轴的距离b=0.0λ、b=20.0λ、b=40.0λ,计算研究目标横向平移的距离b对散射系数σ的影响,计算数值结果如图6所示。

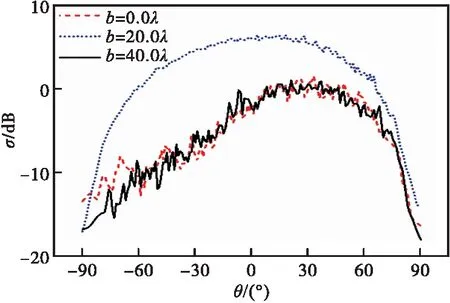
图6 有限深海域海面上方目标横向平移对散射系数的影响

从图6中可以看出,若有限深海域海面上方圆形截面柱仅在水平方向进行平移,复合散射系数σ所受到的影响比较复杂。b=20.0λ时的σ始终是最大的,当b分别取其他两种情形时,σ受到b的影响较小,从图4可以看到,在θs>0°时,b=0.0λ和b=40.0λ时的σ大小非常接近,而在θs<0°时,b=0.0λ和b=40.0λ时的σ仅在θs<-60°时具有比较小的差距。目标的横向平移距离b会改变目标自身的散射特性,对耦合的影响较小,因此复合散射系数σ受到的影响比较复杂。

3.3.3 风速对散射系数的影响

保持其他变量不发生任何变化,分别取有限深海域海面上方风速为5.0 m/s、10.0 m/s、15.0 m/s,计算研究海面上方风速U19.5对散射系数σ的影响,计算数值结果如图7所示。

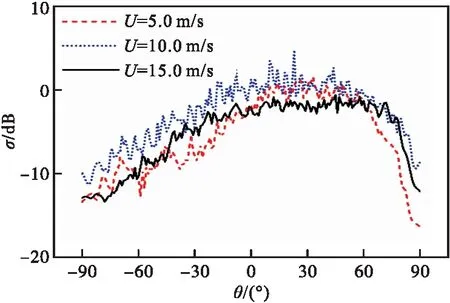
图7 有限深海域海面上方风速对散射系数的影响

从图7可以看出,海面上方风速的变化对复合散射系数σ有较为明显的影响,这是由于海面上方风速变化会引起海面高度起伏的变化,海面与上方目标的复合散射特性由目标散射特性、粗糙面散射特性和两者之间的耦合特性三部分组成,风速的变化会一定程度影响海面的散射特性,同时会对耦合散射特性构成较小的影响,从而复合散射系数会受到较为复杂的影响。

3.4 深水海域海面

若无特殊说明,在深水海域海面情形下,取入射波频率均为1 GHz,入射角θi=30°,海水介电常数εs2=20.0-240i,海水表面风速取U19.5=5.0 m/s;海面上方圆形截面柱目标半径为2.0λ、其重心G到x轴的距离a=2.0λ、到y轴的距离b=0.0λ,深水海域海面采样点1 024个,采样间隔为0.1λ,仿真统计个数100个。

3.4.1 纵向平移对散射系数的影响

保持其他变量不发生变化,取目标重心G到x轴的距离分别为a=2.0λ、a=30.0λ、a=60.0λ,分析讨论目标纵向平移的距离a对复合散射系数σ的影响,计算结果如图8所示。

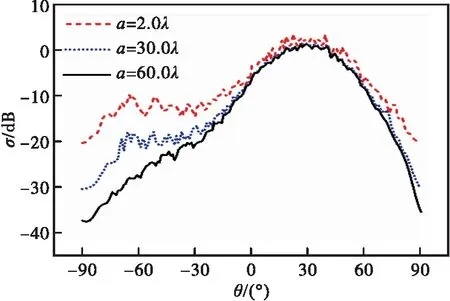
图8 深水海域海面上方目标纵向平移对散射系数的影响

从图8可以看出,目标的纵向平移距离a对复合散射系数σ有着比较规律的影响,与海岸地貌表面情形相似,在所有散射角变化的范围(即-90°<θs<90°)内,除镜反射方向附近的小范围外,均有a越大,σ越小的结论。这是由于海洋对于电磁波的吸收能力更强,而目标纵向移动的尺度越大,距离海面就越远,目标与海面之间的耦合效应也会变弱,因此整个模型的复合散射系数也会变小。

3.4.2 横向平移对散射系数的影响

保持其他变量不发生任何变化,取目标重心G到y轴的距离b=0.0λ、b=20.0λ、b=40.0λ,计算研究目标横向平移的距离b对散射系数σ的影响,计算数值结果如图9所示。

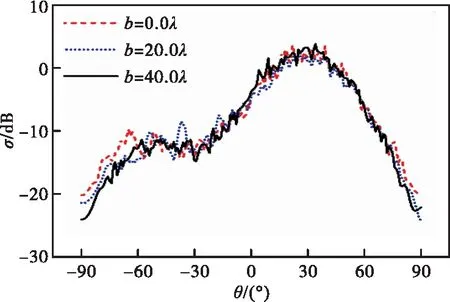
图9 深水海域海面上方目标横向平移对散射系数的影响

从图9中可以看出,若深水海域海面上方目标仅在水平方向进行平移,复合散射系数σ所受到的影响比较小,在整个散射角变化的范围内,σ受到b的影响均较小,b=0.0λ、b=20.0λ、b=40.0λ三种情形下的σ差距较小。总体来讲,深水海域海面上方运动目标的横向平移距离b会对复合散射系数σ造成程度较小的影响,这是由于目标的横向平移只会对目标自身的散射特性造成一定程度的影响。

3.4.3 风速对散射系数的影响

保持其他变量不发生任何变化,分别取深水海域海面上方风速为5.0 m/s、10.0 m/s、15.0 m/s,计算研究海面上方风速U19.5对散射系数σ的影响,计算数值结果如图10所示。

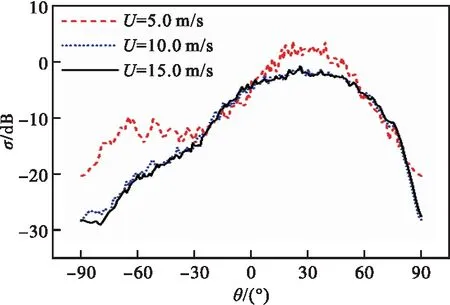
图10 深水海域海面上方风速对散射系数的影响

从图10可以看出,复合散射系数随风速振荡变化,且除散射角处于-30°<θs<0°、45°<θs<70°这两个小区间之外,均有U19.5越大,σ越小的规律,这是由于海面上方风速变大,海谱峰值也随之增大,因此海面高度起伏也增大,此时会有更多散射波被海浪吸收,从而使σ减小。

3.5 不同类型背景上目标散射系数差异分析

保持其他变量不发生任何变化,取目标重心G到y轴的距离b=0.0λ、目标重心G到x轴的距离a=2.0λ,海岸地貌表面介电常数εs1=7.0-2.4i,海水介电常数εs2=20.0-240i,分别计算目标移动至近岸土壤表面上方、有限深海域上方、深水海域上方时的复合散射系数σ,计算数值结果如图11所示。

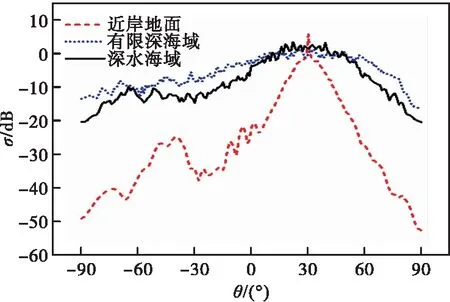
图11 不同类型背景上目标散射系数差异分析

从图11可以看出,当目标从近岸土壤表面上方移动至有限深海域上方时,复合散射系数σ发生了非常明显的变化,这是由于与土壤相比,海水对电磁波的吸收能力更强,因此海水与上方运动目标的耦合效应也就更强,从而当目标移动至海水上方时,复合散射系数σ的值会变大;而当目标从有限深海域移动至深水海域上方时,复合散射系数σ发生的变化较小,这是因为目标在本次移动的过程中,下方介质(即海水)的电性参数并没有发生变化,因此目标与下方介质的耦合效应发生的变化较小,所以复合散射系数σ受到的影响也较小。

4 结论

本文采用矩量法,基于PM海谱、TMA海谱与指数功率谱并结合Monte Carlo方法研究了陆海交界区域粗糙面与上方运动目标的复合电磁散射问题,数值计算了陆海交界区域粗糙面与上方圆形截面柱目标在锥形波入射下的复合散射特性。数值计算结果表明,圆形截面柱在海岸地貌表面与深水海域海面上方纵向平移时对复合散射系数的影响比较显著,而横向平移对复合散射系数造成的影响较小,在有限深海域海面情形下,两种移动方式均会对复合散射系数造成较为复杂的影响。本文还有许多值得改进的地方,例如本文只研究了各自独立的地、海粗糙面模型,自然界中的陆海交界区域是彼此接壤在一起的,这也会一定程度上构成耦合,对于此类陆海交界区域粗糙面与置于其上方或下方运动目标的复合散射问题来讲,还需要进行更进一步的研究。