中部地区高铁可达性演变对区域经济的空间效应研究

唐 卓,蒋惠园,田小勇

(1.武汉理工大学 交通与物流工程学院,湖北 武汉 430063;2.湖南理工学院 经济与管理学院,湖南 岳阳 414006)

中部地区包括晋豫鄂皖湘赣六省,连南接北、承东启西,资源要素丰富,其在全国高铁网络布局与覆盖过程中起着至关重要的连接作用。从《促进中部地区崛起规划》战略的提出,到《新时代推动中部地区高质量发展的意见》发布,国家为中部地区谋划“二次破局”,凸显出国家对中部地区经济一体化发展的重视。高铁包括高速动车组列车(G)、普通动车组列车(D)和城际动车组列车(C)3种车型,作为快速、安全的交通基础设施,高铁可达性提升对区域经济一体化发展具有深远影响[1-2]。因此,研究中部地区高铁可达性演变对区域经济的空间效应,能够促进资源要素流动,加强中部地区各城市之间的经济联系,为高铁建设规划与政策制定提供依据。

可达性是高铁的基础性研究,最常用的测算方法是平均最短旅行时间。姚永鹏等[3]基于加权平均最短旅行时间分析高铁对区域可达性和经济的影响,分析得出高铁能提升区域的可达性。但是,仅考虑平均最短旅行时间来测度可达性,其结果与实际往往偏差较大,学者开始运用多种方法对可达性进行测度分析。何煜超等[4-5]运用日常可达性指数、加权平均最短旅行时间、经济潜力指数等多个评价方法,定量分析了高铁线路建设对地区城市可达性产生的影响。GUTIERREZ[6]运用多个可达性测度方法构建复合评价体系,对法国、马德里等城市的高铁可达性进行评价,并对比分析不同可达性测度方法的公平性,发现研究尺度的差异会影响可达性的测度结果。此外,空间杜宾模型、双层差分模型和耦合协调模型等也是研究高铁可达性与区域经济间关系的重要模型。易其国等[7]应用空间杜宾模型得出高铁对区域经济发展具有显著的空间间接效应,高铁枢纽等级越高的城市其间接效应越强。李姣[8]基于双层差分模型得出高铁可达性提升能重塑生产要素的空间分布,加快人口和资本流动。崔晶等[9-10]应用耦合协调模型分析高铁可达性与区域经济间的作用机理,认为高铁会加快发达城市的虹吸效应,拉大其与贫困地区的经济差距。基于上述研究,笔者提出综合可达性模型,以弥补传统最短时间可达性模型的不足,同时引入地理距离权重矩阵并构建空间杜宾模型,这在中部地区高铁可达性与区域经济的研究方面是一次全新的尝试。

1 研究方法与数据来源

1.1 可达性模型

交通可达性是衡量城市节点间交通便捷程度的重要指标。目前,大多数研究采用平均最短旅行时间AS对可达性进行测度,计算公式为[11]:

(1)

式中:n为研究城市数量,取值为83;Tij为城市i与j间高铁最短旅行时间。

但传统可达性模型仅考虑时间距离,忽略出行到达机会和不同列车开行速度的差异,其测度值往往夸大城市间的可达性。基于此,考虑列车通行时间、类型与数量3个影响因素提出综合可达性模型,更符合实际。先计算综合可达性指数,计算公式为:

(2)

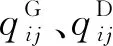
若无直达列车则考虑中转,换乘次数最少为第一原则,通行时间最短为第二原则,并计入换乘时间,则综合可达性A的计算公式为:

(3)

因不同年份有高铁开通的城市数量不同,为使不同年份间有可比性,以2021年为基准年,研究某一城市到其他82个城市的可达性。对于早些年份没有开通高铁的城市,Tij与Hij用非高铁列车数据代替,计算结果也能反映这类城市通高铁前后的可达性变化。

1.2 空间权重矩阵

在交通运输领域地理距离权重矩阵较常见,采用该矩阵对空间属性进行设定。空间权重矩阵W=(wij)n×n的计算公式为:

(4)

式中:wij为城市i对城市j的影响权重;Lij为城市i对j的地理距离。

1.3 空间自相关分析

空间自相关能检验区域某一变量与邻近区域间是否有空间相关关系。全局Moran′sI指数是分析全局空间特征的常用方法,其取值为负则说明两区域具有空间负相关关系,取值为正则说明具有空间正相关关系,其值等于0则说明无空间相关性,绝对值越大空间相关性越强。

(5)

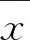
采用统计量Z和P来测定全局Moran′sI指数的显著性程度,P为分布曲线面积近似值,统计量Z的计算公式为:

(6)

式中:E(Moran′sI)、V(Moran′sI)分别为全局Moran′sI指数的期望值和方差。

1.4 空间面板计量模型

空间面板计量模型引入空间权重矩阵,表现空间交互效应,更符合实际。常用的3种模型分别为空间滞后模型(spatial lag model,SLM)、空间误差模型(spatial error model,SEM)与空间杜宾模型(spatial Durbin model,SDM),可通过拉格朗日乘子检验(LM)、稳健性拉格朗日乘子检验(Robust LM)检验、沃尔德检验(Wald)、似然比检验(LR)和豪斯曼检验(Hausman)对模型进行选择。笔者采用空间杜宾模型,与其他两种模型相比,其能同时考虑被解释变量和解释变量的空间自相关。因模型存在偏回归系数,需借助偏微分方程分解得到直接效应和间接效应。直接效应表示本区域自变量对因变量的影响,间接效应表示邻近区域自变量对本区域因变量的影响,直接效应与间接效益之和为总效应。空间杜宾模型的表达形式为:

Yt=(I-lW)-1(bXt+qWXt)+(I-lW)-1ε

(7)

式中:Yt为被解释变量矩阵;I为单位矩阵;l为空间自相关系数;b为解释变量的回归系数;Xt为解释变量矩阵;q为解释变量空间相关系数;WXt为解释变量滞后项;ε为随机扰动项。

对第m个解释变量Xm求偏导,得到用n×n维矩阵表示的边际效应:

(8)

式中:bm和qm分别为Xm及其滞后项的系数估计值。

矩阵E表示区域第m个解释变量变动一单位对所有区域被解释变量产生的影响。直接效应为矩阵E对角线上元素之和再除n,间接效应为矩阵E非对角线上元素之和再除n。

1.5 数据来源

根据高铁发展情况选取5个特征年份,2009年和2012年数据来自《全国铁路旅客列车时刻表》,2015年、2018年和2021年数据来源于“铁路12306”购票软件。

2 中部地区高铁网络可达性时空演变分析

2.1 综合可达性空间演变格局

根据计算结果将综合可达性(Ai)分为6个等级,分别为可达性高水平地区(187～300]、较高地区(300～480]、中等地区(480～660]、一般地区(660～840]、较低地区(840～1 020]、低水平地区(1 020～1 325]。中部地区高铁网络综合可达性演变情况如图1所示。

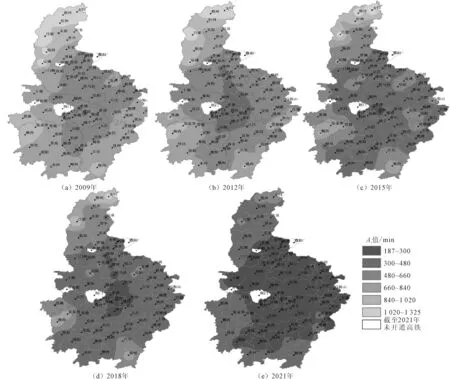
图1 中部地区高铁网络综合可达性演变图

由图1可知:①2009年,可达性较高地区主要分布在武汉、孝感和信阳等中心区域;可达性中等地区包括郑州、合肥、长沙和南昌等35个地级市,城市数量多且紧密围绕在可达性较高区域外围;可达性一般地区包括太原等33个地级市,围绕可达性中等地区形成东、西、南半包围态势;可达性较低及以下地区主要分布在山西、湘鄂西部等边缘区域。②2012年,可达性较高地区主要集中在京广线郑州至长沙段周围,东扩至合肥,南扩至长沙,西扩至潜江;可达性中等及以上地区进一步向四周呈图层式扩展;可达性一般及以下地区仍集中在山西、湘鄂西部及赣南片区,主要是由于列车总体班次不多且区域位于地域边缘,具有一定的独立性。③2015年,武汉、孝感和信阳首次进入可达性高水平地区,可达性较高地区范围也进一步蔓延,覆盖中部地区近三分之二区域;可达性中等及以下地区分布空间进一步压缩,较低及以下地区仅剩晋北片区和湘西。④2018年,可达性高水平地区进一步沿京广线向四周蔓延,湘西和忻州可达性进入到一般及以上水平,较低及以下地区仅剩晋西的吕梁和晋北的朔州、大同。⑤2021年,可达性提升幅度最大,总体空间格局最为简单,除吕梁、朔州和大同外,其他80个城市可达性都进入较高及以上水平,可达性高水平城市增至57座,主要覆盖中东大片区域;较高水平城市增加至23座,主要分布在西部、南部和北部边缘区域。

2.2 综合可达性与最短时间可达性对比

为对比分析综合可达性与最短时间可达性(ASi)两种计算方法的优劣,以进一步了解两种计算方法在反映高铁可达性上的差异。采用两种可达性的差异率((Ai-ASi)/Ai)进行对比分析,差异率演变如图2所示,可知两种可达性总体差异率维持在0%～16%之间。为确保不同年份间有可比性,将可达性差异率分为6个等级,分别为低差异率(2%～4%]、较低差异率(4%～6%]、一般差异率(6%～8%]、中等差异率(8%～10%]、较高差异率(10%～12%]和高差异率(12%～16%]。相比而言,最短时间可达性都偏低,但不同年份间差异率的空间分布存在差异。①2009年,两种可达性差异率主要以较低及以下为主,其中较低差异率范围基本覆盖了东部、中部和西部,山西西北部和湘赣南部等边缘地区是低差异率分布的集聚区。此时,中部地区有高铁的城市不多,高铁班次也较少,因此两种可达性计算结果差异不明显。②2012年,差异率呈增大趋势,中部与外围形成圈层式分异格局,河南和湖北大部分地区上升到一般差异率级别,主要是由于这两个省份处于地理中心位置,高铁班次多且不同列车速度有差异;而其他省份大部分地区由于高铁建设缓慢,出行列车类型选择有限,大部分地区都继续维持在6%以下的较低差异率。③2015年,差异率形成相对破碎化的空间格局,中等差异率及以上的高值区主要分布在湖北东北部、河南北部和安徽东南部,较低差异率及以下的低值区则主要分布在山西北部、湘鄂西部和湘赣南部,其他地区则以一般差异率覆盖为主。④2018年,中等差异率覆盖范围沿东西方向进一步延伸成片,覆盖湖北大部分城市和安徽南部片区。较低差异率及以下的覆盖范围进一步缩减,表现为散点状和小片区组团分布。⑤2021年,可达性差异率空间格局发生巨大变革,绝大部分城市都在中等差异率及以上,尤其是湖北、河南、湘赣北部等地理中心区域,整体上呈现由中向外发散覆盖的态势。

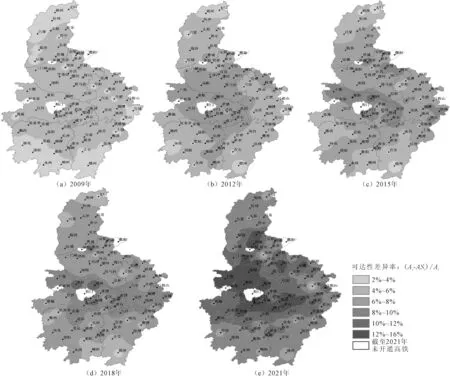
图2 两种可达性计算方法间差异率

3 中部地区高铁可达性演变对经济发展的空间效应研究

3.1 变量设定

考虑到区域经济发展通常是多因素共同作用的结果,因此在选取综合可达性和最短时间可达性为核心解释变量的基础上,进一步引入多个控制变量进行综合分析。

(1)被解释变量:经济发展水平。由于各地区人口基数不同,选用地区人均生产总值(PGDP)反映地区间经济发展的差异。

(2)核心解释变量:可达性水平。为了进一步比较两种可达性对区域经济发展空间效应的差异,分别选用综合可达性(Ai)和最短时间可达性(ASi)作为模型1和模型2的核心解释变量。

(3)控制变量:①资本水平(K),用实际固定投资总额来衡量;②城镇化水平(U),U=城市城镇人口/城市总人口;③第三产业水平(IND),IND=第三产业增加值/总GDP;④开放程度(OPEN),OPEN=外商投资企业工业总产值/总GDP;⑤劳动力(LAB),用年末单位从业人员数来衡量;⑥科教水平(RD),RD=科学和教育支出/财政支出;⑦社会建设(SC),SC=博物馆数+体育场馆数+公共图书馆数+影剧院数+普通高等学校数。考虑到不同控制变量数据形式的差异性,对以上7个控制变量进行对数化的平稳性处理。

3.2 空间关联特征分析

利用Stata软件得到地理距离权重矩阵下PGDP、Ai和ASi的全局Moran′sI指数变化情况,如表1所示。不难发现,各个年份PGDP、Ai和ASi的全局Moran′sI值均大于0,并通过显著性检验,说明上述3个指标都存在全局空间正向自相关性,相邻城市间会相互影响,可以采用空间计量模型进行分析。

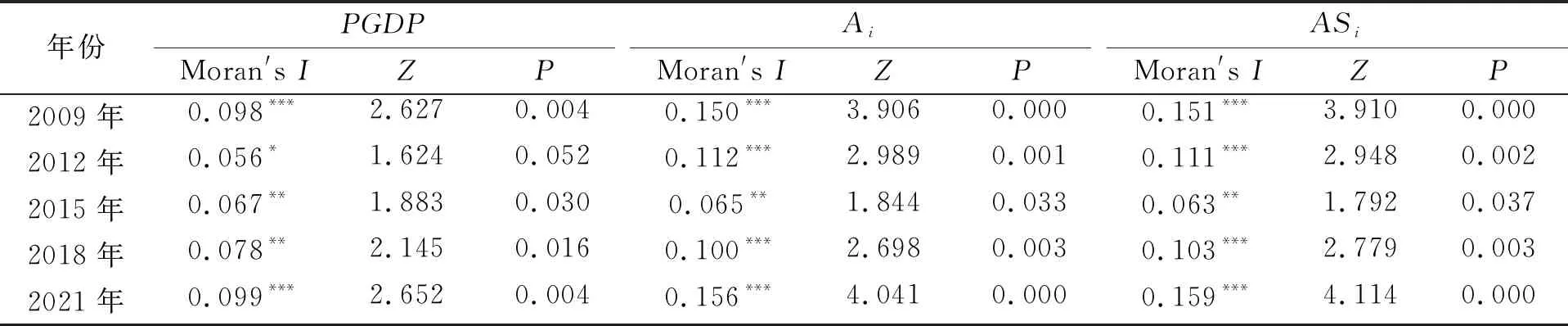
表1 主要指标的全局Moran′s I指数

为考虑城市间可能存在的关系,进一步探究局部空间关联特征,运用Stata软件进行局部空间自相关检验,绘制首尾两年主要指标的局部Moran散点图,如图3～图5所示,可以看出随着时间的发展,交通可达性对中部地区社会经济发展的影响趋于稳定,越来越多城市集中于一、三象限,说明这些城市的PGDP、Ai和ASi存在明显的空间正相关。

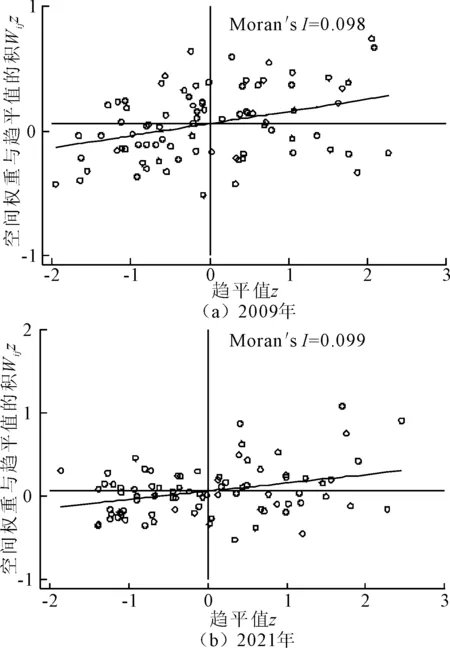
图3 2009年、2021年PGDP局部空间自相关检验图

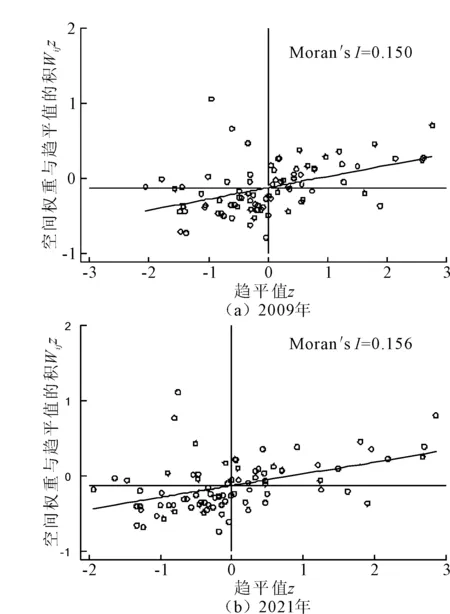
图4 2009年、2021年Ai局部空间自相关检验图

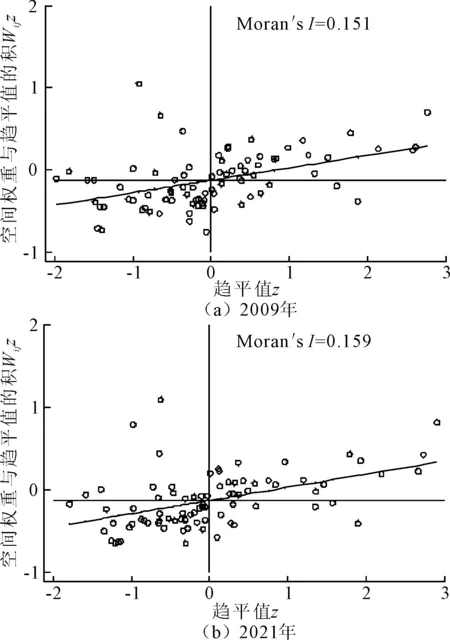
图5 2009年、2021年ASi局部空间自相关检验图

3.3 估计模型识别与结果分析

在空间关联特征分析的基础上,进一步检验空间关联性的具体存在形式,检验结果如表2所示。从表2可以看出,模型1(Ai)与模型2(ASi)的LM和Robust LM都通过了显著性检验,说明两个模型都具有空间误差和滞后的特征。Wald及LR检验都不允许将空间杜宾模型简化为空间误差模型或空间滞后模型。Hausman检验统计值分别为88.220和79.700(P=0.000),能够确定应用固定效应模型更加合适。综上所述,最终选择固定效应空间杜宾模型进行实证分析。

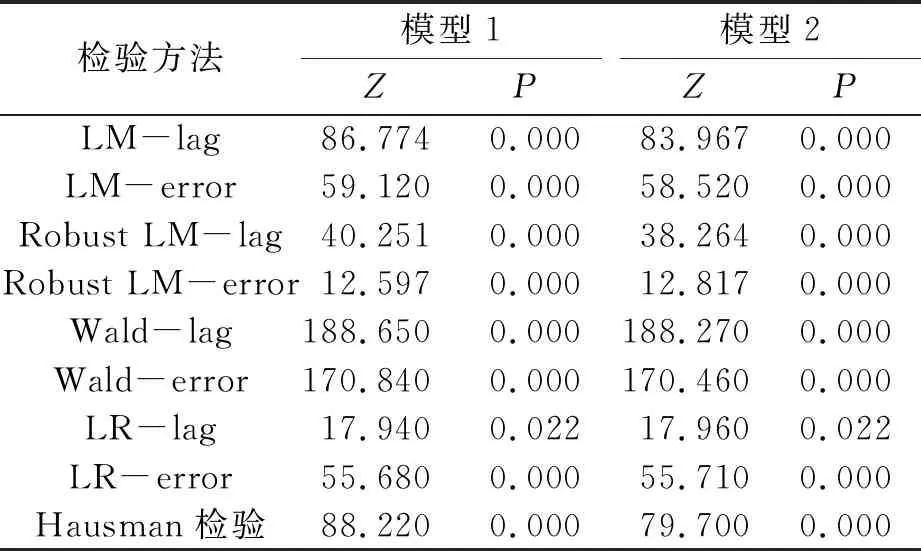
表2 空间计量模型的检验结果

为判断空间模型选取的合理性,先对空间模型做最小二乘估计(OLS),再进行空间杜宾模型估计,估计结果如表3所示。模型1中,在估计系数上OLS模型和SDM模型的空间固定效应存在明显差异,其值分别为0.278和0.131,表明综合可达性对城市经济发展不断产生影响。由于OLS模型没有考虑城市之间的空间依赖性,忽略了因变量和自变量的空间间接效应而高估了综合可达性对城市经济发展的影响。模型2也支持这种观点。从空间相关系数的角度看,两种模型的空间相关系数(rho)都为0.539,均在1%的水平下显著,故存在正向间接效应,这说明邻近城市可达性水平提升会对本地区经济增长带来促进作用。

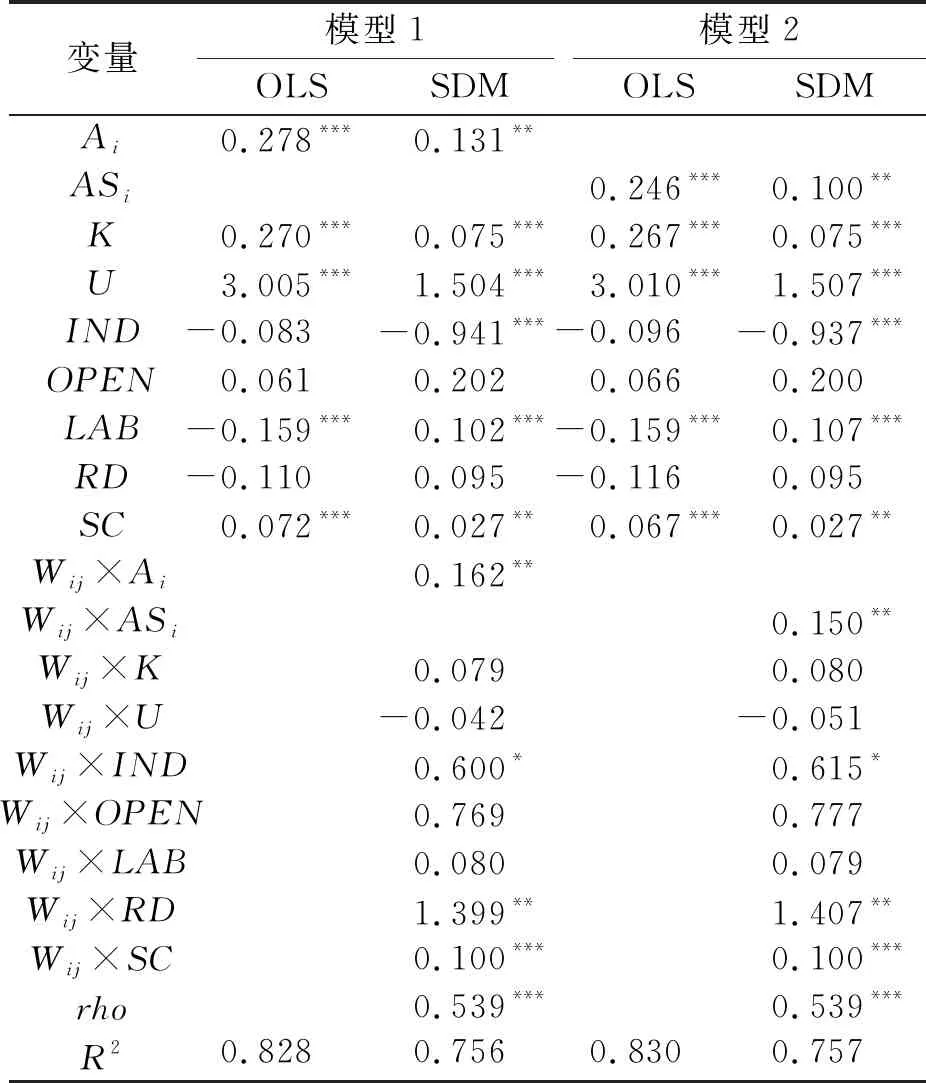
表3 OLS和SDM模型估计结果

3.4 区域整体层面的空间效应分解

为了更精准地刻画Ai和ASi对经济发展格局的影响,进一步采用偏微分方法分解出核心解释变量和控制变量的直接效应、间接效应和总效应,计算结果如表4所示。

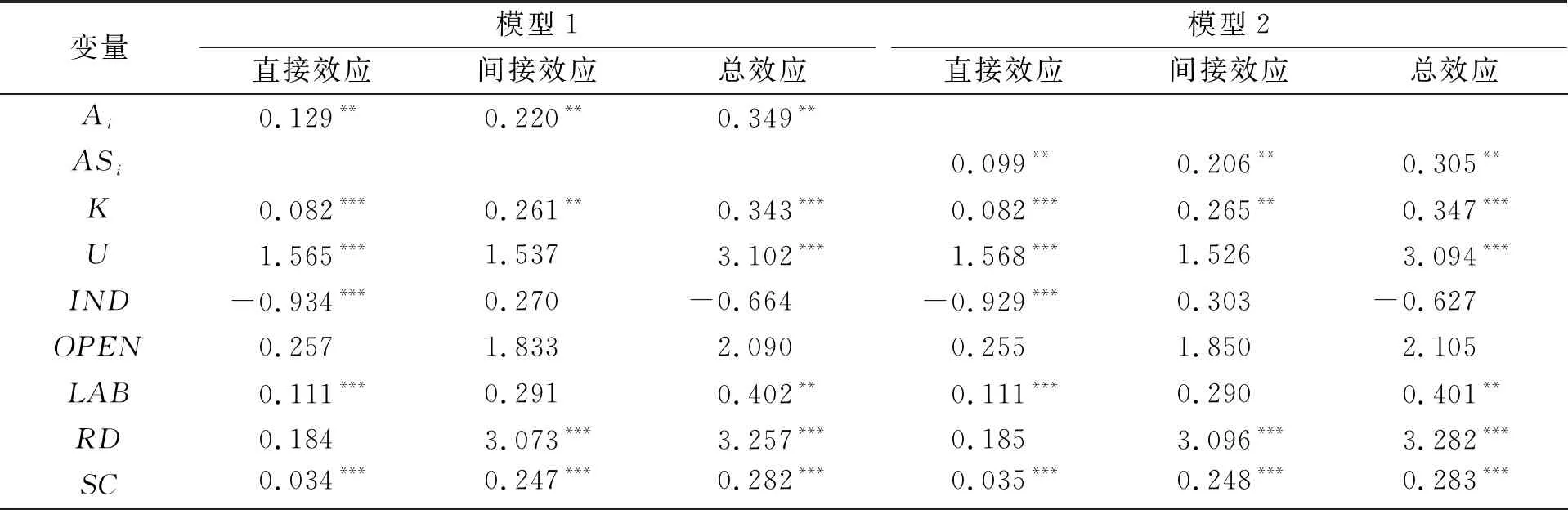
表4 空间效应分解

在模型1中,Ai对经济发展既存在正向空间直接效应,也存在正向空间间接效应,具有较强的一致性。其中,Ai的直接效应为0.129,间接效应为0.220,均通过了5%的显著性水平检验,表明本地区Ai每提升1个单位,将带动本地区0.129的经济发展和邻近地区0.220的经济增长。由此可见,Ai的间接效应大于直接效应,对周边地区的影响作用超过对本地区的影响。因此,构建完善的交通网络体系是推动区域经济一体化发展的重要措施。

模型2选取ASi作为核心解释变量,其对经济发展也存在正向空间直接效应和正向空间间接效应,并且在5%的水平下显著,表明本地区ASi每提升1个单位,将带动本地区0.099的经济发展和周边地区0.206的经济增长。但由于ASi忽略高铁类型、时间成本和客运结构的差异,其对经济发展的间接效应要小于Ai。这也在一定程度上表明交通基础设施发展速度过快会强化对周边地区经济发展资源要素的虹吸效应,削弱其对周边地区经济发展的间接效应。此外,其他控制变量或多或少也对经济发展产生不同程度的影响。

总之,不论哪种计算方式,交通可达性的提高都会促进本地区和邻近地区社会经济的发展,从模型的角度来说,这一结论在整体层面上是稳健的。随着高铁网络的发展,城市间交通可达性得到了较大提高,这对促进生产要素的流动起到了重要作用,对本区域和周边区域的经济发展创造了利好条件。

4 结论

(1)综合可达性空间格局演变总体呈现“核心-边缘”圈层式特征,位于几何中心的城市与其他城市通行时间更短,边缘城市通行则较为不便。中部地区综合可达性平均计算值由2009年的711.480降至2021年的292.040,高铁网络发展对城市联系的时空压缩效应明显,地区协同发展距离屏障逐渐削弱。

(2)综合可达性与最短时间可达性间的差异长期存在,并随着高铁网络发展,差异有着愈加显化的趋势。在2009年,两种可达性总体差异率位于4.610%的较低水平,然而随着高铁类型及班次可选择性越来越多,到2021年两种可达性总体差异率达到10.440%,此时最短时间可达性将过度优化实际可达性水平。

(3)高铁可达性的提升会促进本地区和邻近地区社会经济的发展。综合可达性的直接效应和间接效应分别为0.129和0.220,最短时间可达性的直接效应和间接效应分别为0.099和0.206,两种可达性的间接效应皆大于直接效应,经济发展受邻近地区可达性的影响更大,故未来高铁建设规划应注重均衡化布局,在规划本地区高铁线路的同时,邻近地区的高铁建设规划也应提上日程,这更有利于本地区经济发展。最短时间可达性的间接效应小于综合可达性,可达性提升过快会强化对周边地区经济发展的虹吸效应,削弱其对邻近地区经济发展的间接效应,在未来制定相关政策来宏观调控地区间高铁可达性差异率,促进邻近地区经济发展的同时,谨防虹吸效应,才是实现地区均衡高效发展的关键。

(4)由于连续年高铁时刻表数据收集与处理难度较大,仅选取2009年、2012年、2015年、2018年和2021年5个特征年份进行分析,非连续年数据在测算结果上可能相对粗略。未来借助流动大数据平台获取连续年客流量数据,有望更加精确识别中部地区高铁可达性演变规律。