国际集装箱海运服务多边多目标匹配研究

兰龙辉,李登峰

(1.福州大学 经济与管理学院,福建 福州 350108;2.电子科技大学 经济与管理学院,四川 成都 611731)

在国际贸易活动中,因海洋运输具有运价低、运量大、运距远的优势,集装箱海运已成为国际物流中最主要和最广泛的运输方式之一。根据国际货运代理协会联合会(FIATA)统计,2/3以上的全球贸易总运量和近90%的中国进出口货运总量都是利用集装箱通过海洋运输完成。由此可见,海运业对于国际贸易的重要作用。我国法律规定,进出口贸易企业无法直接从事国际货物运输业务,必须找有资质的国际货物运输代理企业(以下简称货代公司),代为其办理各类进出口货运手续。进出口贸易商在国际海运物流的单证体系中习惯称之为发货人和收货人,以出口货物为例,出口商为发货人,进口商则为收货人。船公司,也称船东,作为货物的实际承运人,负责将指定货物在指定时间内从指定的起运港运输到指定的目的港,并交付于指定收货人,至此完成国际集装箱海运的运输任务。货代公司作为资源型平台公司,基本经营模式是从外部采购各方资源(包括船东、拖车、仓库、保险公司等)为进出口商提供国际物流服务,并从中收取服务报酬。因此,在国际集装箱远洋运输中,货代公司通过整合多项国际物流资源和客户需求,进而为各方利益主体匹配到相应的物流服务。

现实中,货代公司掌握最新最全的市场信息,为客户提供海运物流服务方案时存在高报运价、错报船公司船期信息等行为,造成收、发货人的利益受损。同时,收、发货人也会发生谎报货物信息、拖欠账款等现象,导致货代公司、船公司的收益降低。针对上述市场行为,为减少信息不对称对国际海运物流效益的影响,使得国际集装箱海运物流活动的各方能够做出更加科学、公平和高效的决策,出现了多种智能匹配辅助决策系统。例如,Flexport开发的Ocean Match模块,可帮助发货人快速找到最适合的国内外物流服务提供商;运去哪的线上系统则提供了在线匹配业务功能,可根据发货人的国际物流服务要求,自动获取货代公司的报价信息。但是,目前上述匹配平台尚处于推广期,且仅考虑了某一主体的匹配需求,匹配指标较为单一,无法满足多指标下多方主体的匹配诉求。因此,为解决现有匹配指标、匹配主体单一的问题,将在货代公司构建的国际集装箱海运服务匹配平台上,最大化发货人、船公司和收货人的匹配满意度,提出多指标多边的匹配模型。

匹配问题最早由GALE等[1]提出,其对婚姻稳定和入学招生情况进行了开创性研究,提出Gale-Shapley算法并成功解决了婚姻匹配问题,证明稳定的婚姻匹配总是存在的。ROTH[2]于1985年首次提出“双边”和“双边匹配”的概念,之后对美国医学院毕业生与实习医院的匹配进行了研究。此后,关于双边匹配的研究成果不断出现,匹配理论在经济管理领域也得到大量的实践应用。陈希等[3]将双边匹配理论应用在IT服务外包中的供给方和需求方,用语言变量表示双方的评价信息,以供需双方满意度最大为目标,构建了IT服务供需双边匹配的多目标模型。万树平等[4]针对风险投资商与投资企业的双边匹配问题,基于前景理论,采用模糊数表示匹配指标,进而构建双边主体的总体满意度,最后建立风险投资商、投资企业总体满意度最大化和投资中介收益最大化的多目标优化模型。在匹配问题研究中,匹配指标一般表现为多属性,如何将异质匹配指标进行集结也是匹配问题研究的核心。许颖等[5]考虑隶属度、非隶属度、犹豫度之间的关系,构建出新的q阶区间Orthopair模糊集记分函数,依据成熟的前景理论,提出基于参考点相依效用函数的模糊多属性决策方法,并通过疫苗投资的多属性决策问题验证该方法的有效性。骆华[6]采用犹豫度公式计算概率犹豫模糊元的犹豫性,用信息不完全度公式测量概率犹豫模糊元的不完全性,结合元素数值间的差异,重新定义了改进后的距离公式,并将改进后的距离公式与TODIM方法相融合,构建出概率犹豫模糊多属性决策模型。

综上可知,国内外关于匹配问题的理论和应用研究较多集中在双边匹配,且匹配满意度的表达无法适用于不同的现实场景。而关于多指标决策问题的研究则主要侧重于指标值的表达和信息的集结方法[7]。针对具有多方匹配主体、多指标评价体系的国际集装箱海运服务的匹配研究较为稀少,现有研究也无法从多指标多方主体的利益需求出发,描述进出口贸易商、船公司的匹配满意度以及前后匹配主体的逻辑关系。因此,笔者将从实际需求出发,通过建立多指标多边匹配评价体系,提出一种全新的匹配主体综合满意度表达方式,以刻画国际集装箱海运服务的匹配特点;此外,受匈牙利算法思想的启发,设计出一种更加符合海运服务匹配要求的算法。

1 匹配指标体系构建

1.1 问题描述

在整个国际集装箱远洋运输中,涉及的重要主体为发货人、船公司、收货人。国际集装箱远洋运输的一般化流程可以概述为:货物由发货人按照约定的贸易条款(包括商品的价格、数量、品质等信息),以集装箱为载体,经由船公司经营的远洋货轮进行运输,最后将货物定时定点送达指定收货人。该过程的核心匹配问题是为已经确定买卖关系的发货人和收货人,通过某种科学决策方法,在供过于求的国际集装箱运力市场中找到船期适合、价格适合、综合满意度高的船公司。货代公司因其掌握国际集装箱海运市场上下游的资源,通过撮合物流服务需求方和运力的供应方,为各方主体匹配到满足自身利益诉求的服务。因此,货代公司具备构建匹配平台的天然优势。

考虑在相同的起运港和目的港的情况下,发货人与收货人为一一对应的买卖关系,即一个发货人只有一个收货人,一个收货人有且只有一个发货人。基于不同主体视角,在货代公司搭建的海运匹配平台上,构建合理的多指标多边匹配模型,建立最大化三方匹配主体的满意度函数。国际集装箱海运服务匹配决策的示意图如图1所示。

图1 国际集装箱海运服务的多边匹配示意图

1.2 符号定义与说明

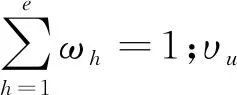
1.3 三方匹配指标的选取与表达

1.3.1 匹配指标的选取

根据实际调研情况分别对发货人、船公司和收货人的匹配需求进行分析,构建对应的匹配指标。从发货人的视角来看,其最关心的是实际负责远洋运输船公司的海运价格P1(以20GP的集装箱为例,区间数)、允许账期P2(支付船公司费用时被允许的最长时效、区间数)、货轮的开航时间P3(货轮离港时间,实数)。从船公司的视角来看,其是国际集装箱远洋运输的实际承运人,既关注处于上游的发货人,也关注处于下游的收货人,船公司对于发货人的评价指标可以总结为:公司信誉D1(发货人在海运市场中的信誉度,语言变量)、出货准时率D2(发货人按照约定时间和地点进行装车装船的准时度,语言变量)、回款账期D3(发货人支付船公司费用时被允许的最长时效,区间数);船公司对于收货人的评价指标可以归纳为:公司信誉E1(收货人在海运市场中的信誉度,语言变量)、收货准时率E2(收货人按照约定时间和地点进行卸车卸船的准时度,语言变量)、回款账期E3(收货人支付船公司费用时被允许的最长时效,区间数)。从收货人的视角来看,其是国际物流活动的终端,最关注的是负责实际承运的船公司的行业信誉G1(船公司在海运市场中的信誉度,语言变量)、允许账期G2(收货人支付船公司费用时被允许的最长时效,区间数)、到港时间G3(货轮到港时间,实数)。

1.3.2 匹配指标的数据类型

根据上述匹配指标,三方匹配主体针对匹配指标给出对应的期望值,给出的期望水平经常是多种不同形式下的定量和定性的指标值。对于定量指标,可能以实数或区间数表示,如某出口公司期望上海港到泰国曼谷港的海运费报价为1 000～1 200美元/标箱(以常用的20GP集装箱为例),记作闭区间[1 000,1 200]。而船公司的报价一般为确定的实数,如1 100美元/标箱,实数可以看成区间数退化后的特例,因此可以写成区间形式[1 100,1 100]。对于定性指标而言,一般以语言变量形式给出,如评价公司的信誉度、出货准时率等,使用“非常高”、“很高”等语言变量来描述。带有语言变量的匹配指标是评价主体根据主观感受给出的一种指标强弱程度化的表达形式,笔者采用描述指标更加细腻的七粒度语言评价集合。针对决策过程中的语言变量,参照传统做法,将语言变量转化为三角模糊数后再进行指标的量化处理[8-10]。

2 匹配指标满意度函数

在国际集装箱海运服务匹配过程中,3个主体的9个匹配指标均采用实数、区间数及语言变量进行表示,在这些匹配指标中,有的指标取值越大越好,如出货准时率,称之为效益型指标;有的指标值则是越小越好,如对于发货人来说船公司给出的海运价格越低越满意,称之为成本型指标[11-12]。对两种不同数据类型的匹配指标分别进行满意度函数的构建。

2.1 区间型匹配指标的满意度

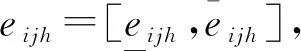
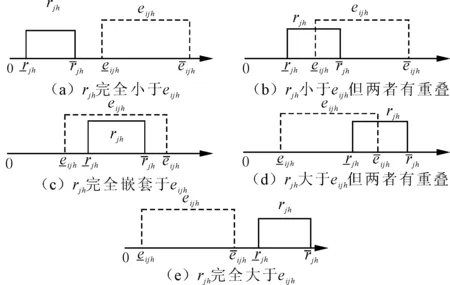
图2 区间数eijh与rjh的5种位置关系

通过观察期望值eijh和实际值rjh的相对位置关系,可以得出匹配主体在对应指标下的满意度,即两个区间数重合的区间越多,甚至实际值远大于期望值,则在该指标下的满意度越高[13]。基于决策者往往以期望值作为评估得失的心理特征,通过匹配指标期望水平与实际水平的比值刻画发货人Fi对于船公司Cj在区间效益型指标Ph下的匹配满意度αijh,即:

αijh=

(1)

式中:“>I”表示两个区间数的排列顺序关系。

(2)成本型指标。若匹配指标为区间成本型,即指标值越小匹配主体的满意度越高。同样地,通过观察区间成本型匹配指标的期望值eijh与实际值rjh的相对位置关系,可以得出匹配主体在对应指标下的满意度,此时,发货人Fi对于船公司Cj在区间成本型指标Ph下的匹配满意度αijh可以表示为:

αijh=

(2)

2.2 语言变量型匹配指标的满意度

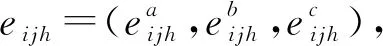
效益型指标:αijh=

(3)

成本型指标:αijh=

(4)

式中:符号“>T”表示两个三角模糊数的顺序关系。

同理,依次可以获得在区间效益型指标、区间成本型指标、语言变量效益型指标和语言变量成本型指标下不同匹配主体的单独满意度,即船公司Cj对发货人Fi在指标Du下的满意度βjiu、船公司Cj对收货人Sk在指标Ev下的满意度δjkv和收货人Sk对船公司Cj在指标Go下的满意度γkjo。

2.3 匹配满意度的集结

(1)指标权重的确定。通过式(1)～式(4)计算得到某个匹配主体在单个指标下的匹配满意度,由于国际集装箱海运物流的匹配模型是多指标下的匹配,需要赋予每个匹配指标不同的权重。匹配指标Ph、Du、Ev和Go的权重分别为ωh、υu、θv和ηo,可以采用层次分析法AHP或行业专家打分法确定。

(2)匹配满意度的集结。依次获得每个指标的匹配满意度和对应指标权重后,根据线性加权法,对所有匹配指标满意度进行集结,可得到该匹配主体的综合满意度,即发货人Fi对于船公司Cj在匹配指标集合P下的综合满意度πij、船公司Cj对发货人Fi在匹配指标集合D下的综合满意度πji、船公司Cj对收货人Sk在匹配指标集合E下的综合满意度πjk、收货人Sk对船公司Cj在匹配指标集合G下的综合满意度。

(5)

(6)

(7)

(8)

3 多边多目标匹配模型构建与求解

3.1 构建多边多目标匹配模型

根据现实场景,基于不同主体角度分析,构建国际集装箱海运物流的多边多目标匹配模型。模型仅考虑一个发货人对应一个收货人的海运服务匹配问题,因此假定发货人与收货人的人数相同,即l=n。把这种一个发货人只对应一个收货人的确定关系表示为一个集合Ω={(α,β)|发货人α对应的收货人β}。

从发货人的利益来看,其具有优先选择船公司的权利,重点考量对船公司各项指标的满意度。同时,为保证海运任务的顺利进行,还需要兼顾考虑到船公司对某一确定收货人的评价,如收货人在历史交易中是否存在拖欠账款现象,收货效率如何等。因此,从发货人角度考虑的匹配链条可以表示为:发货人Fi→船公司Cj→收货人Sk。作为国际贸易的正向物流,两个匹配环节的满意度必须同时达到发货人和船公司的要求才能算完成匹配任务,所以前后两段匹配的整体满意度表现为连乘关系,记作μf,即:

(9)

从货物实际承运人船公司的视角出发,其既考虑对上游发货人评价指标的满意度,又要考虑对下游收货人评价指标的满意度,具备根据匹配指标选择发货人和收货人的权利。所以,从船公司角度考虑的匹配链条可以表示为:发货人Fi←船公司Cj→收货人Sk。同样地,上下两段匹配的满意度也采用连乘关系来刻画。因此,从船公司角度考虑的整体满意度μc为:

(10)

从国际物流末端的收货人角度出发,其重点考量对船公司评价指标的满意度,此时,收货人具备选择船公司的权利。同时,还必须考虑到船公司对指定某一发货人的匹配满意度,匹配链条可以表示为:发货人Fi←船公司Cj←收货人Sk,前后两次的满意度也采用乘号进行连接。因此,从收货人角度考虑的整体满意度μs为:

(11)

由此,建立国际集装箱海运物流的多边多目标匹配模型:

max{μf,μc,μs}

(12)

(13)

xij=0或1(i=1,2,…,l;j=1,2,…,m)

(14)

xjk=0或1(j=1,2,…,m;k=1,2,…,n)

(15)

在该模型中,式(12)为目标函数,表示最大化分别从发货人、船公司和收货人三个主体出发考虑的满意度;式(13)表示经过所有船公司只能把发货人的货物运输给相应的固定收货人,确保发货人和收货人一一对应;式(14)和式(15)为0-1变量约束,xij=1表示发货人和船公司匹配成功,否则匹配失败;xjk=1表示船公司和收货人匹配成功,否则匹配失败。

3.2 模型求解

3.2.1 模型转化

上文建立的是非线性的多目标0-1整数匹配模型,采用传统的求解方法非常困难甚至无法求解得到0-1整数解。通过观察模型特点和国际集装箱海运匹配问题的行业特征,受匈牙利算法的启发,设计该模型的有效求解方法。①采用线性加权方法,将多目标匹配模型转化为单目标模型进行求解[15-16]。为保证三方海运匹配主体的公平性,设每个目标的权重为1/3。因此,上述多目标匹配模型可转化为单目标模型,如式(16)所示。②国际集装箱海运匹配问题的本质是为确定关系的发货人和收货人匹配到满意度最大的船公司,由于发货人和收货人在匹配之前就已经为确定的贸易关系,可将发货人和收货人视为一对确定关系的贸易组合。由此,借鉴指派问题的思想,将三方主体的匹配问题转化为整数规划中的指派问题。③借用匈牙利算法思想,对模型进行求解。

(16)

将确定收发关系的贸易组合即集合Ω={(α,β)|发货人α对应的收货人β}中的任意元素看作“人”,负责实际承运的船公司Cj看作“事”,贸易组合对船公司的整体满意度作为满意度矩阵。

3.2.2 模型算法设计

将多目标匹配模型转换成类似指派问题后可知,这是一类特殊的整数规划问题,即特殊的0-1规划问题,借用匈牙利籍数学家康尼格提出的关于矩阵中独立零元素的定理来求解该问题,因此称之为匈牙利解法[17]。该定理已证明若从指派问题的系数矩阵C的某一行(或某一列)各元素同时减去一个常数K,得到新的系数矩阵C′,此时以C和C′为系数矩阵的指派问题具有相同的最优解。国际集装箱多目标匹配问题转化为指派问题后的模型算法步骤:①以发货人和收货人建立的贸易组合作为行、船公司作为列,他们之间相应的整体满意度为矩阵的元素,构成满意度矩阵C。②选出满意度矩阵中最大值,记作M。③用最大值M减去满意度矩阵中所有元素,获得新的满意度矩阵C′。④找出含有零元素的行,划掉这些行。⑤从划掉行后剩余的满意度矩阵中继续找出其中的最大值M′,重复步骤②～步骤④。⑥若所有行都被划去,则获得最优匹配,否则转入步骤⑤。

值得注意的是,变换后的满意度矩阵中某行可能存在多个零元素,表示贸易组合对于零元素所对应的多家船公司的满意度相等,但是最终有且只能选择其中一家船公司进行运输;变换后的满意度矩阵中某列允许同时存在多个零元素,表示一家船公司可以同时承担多组运输任务,符合现实匹配场景。

4 实例分析

国际集装箱海运匹配平台收到如下匹配任务:5个发货人需从起运地上海港出口货物到目的地德国汉堡港、3家符合起讫港要求的船公司和5个在目的港的收货人。发货人和收货人组成5组一一对应的贸易关系:(长荣贸易F1,沃尔玛S5)、(升升材料F2,普兰电子S1)、(新世界家居F3,奥瑟商贸S2)、(徐记F4,茨尔林业S3)、(大唐木业F5,斯特家居S4),即发货人与收货人一一对应关系集合为Ω={(1,5),(2,1),(3,2),(4,3),(5,4)}。船公司分别为MSK马士基航运C1、MSC地中海航运C2和COSCO中远海运C3。模型仅考虑货物为整箱的情况,即一个集装箱仅有一名货主,不存在拼箱货,海运费以20GP箱型的集装箱为单位进行报价。

4.1 数据来源

国际集装箱海运匹配平台根据三方客户提交的匹配需求和实际调研情况,统计给出了三方匹配主体在不同评价指标下的期望水平和实际水平,具体如表1～表8所示。

表1 发货人对船公司关于指标P1与P2的期望水平

表2 船公司关于指标P1与P2的实际水平

表3 船公司对发货人关于指标D1、D2和D3的期望水平

表5 船公司对收货人关于指标E1、E2和E3的期望水平

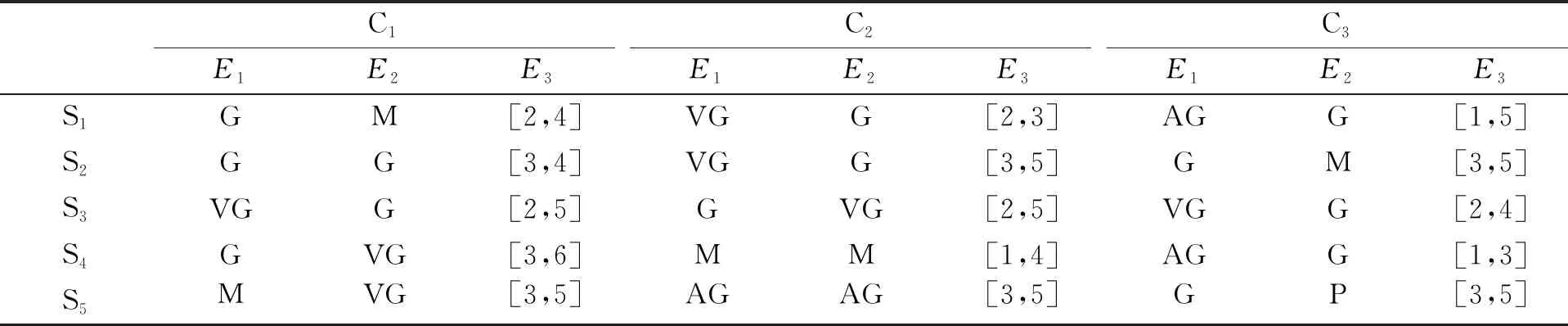
表6 收货人关于指标E1、E2和E3的实际水平

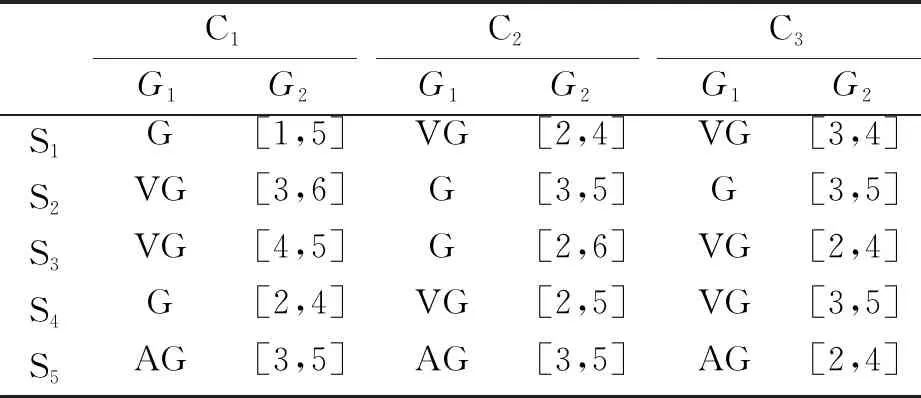
表7 收货人对船公司关于指标G1、G2和G3的期望水平

表8 船公司关于指标G1和G2的实际水平

鉴于某一家的发货人对于发货的时间是确定的,即同一发货人对任意一家船公司的期望开航时间P3是相同的,F1期望的开航时间为20221205,F2期望的开航时间为20221231,F3期望的开航时间为20221201,F4期望的开航时间为20221204,F5期望的开航时间为20221210。

同理,同一家船公司对于任意一家发货人来说开航日期P3都是相同,C1的实际开航时间为20221206,C2的实际开航时间为20221209,C3的实际开航时间为20221205。

由于某一的收货人对于期望的收货时间是确定的,即同一收货人对于任意一家船公司的到港时间要求G3是相同的,收货人S1期望的到港时间为20221231,收货人S2期望的到港时间为20230110,收货人S3期望的到港时间为20221215,收货人S4期望的到港时间为20221231,收货人S5期望的到港时间为20230108。

同理,由于每个船公司的到港时间是确定的,即同一家船公司对于任意一家收货人的实际到港时间都是相同的,C1的实际到港时间为20230102,C2的实际到港时间为20230106,C3的实际到港时间为20230110。

4.2 模型计算

国际集装箱海运匹配平台获得三方匹配主体之间相互评价的期望值和实际值后,首先,根据匹配指标所属的4种类型,分别利用式(1)～式(4)计算单个主体在单个评价指标下的满意度。其次,组织行业专家评议各匹配指标的权重,考虑到船期要求和回款账期是海运市场中最重要的两项指标,最终确定各指标的权重向量为:ωh=(0.2,0.2,0.6)T,υu=(0.3,0.3,0.4)T,θv=(0.3,0.3,0.4)T,ηo=(0.2,0.2,0.6)T,再利用式(5)～式(8)求得某个匹配主体在对应指标集合下的集结满意度。再次,根据式(9)～式(11)分别获得前后两段具有连乘关系的三方主体利益角度下的整体满意度。最后,通过式(16)将三方的整体满意度进行集结,得到三方互相评价后的最终满意度,如表9所示。

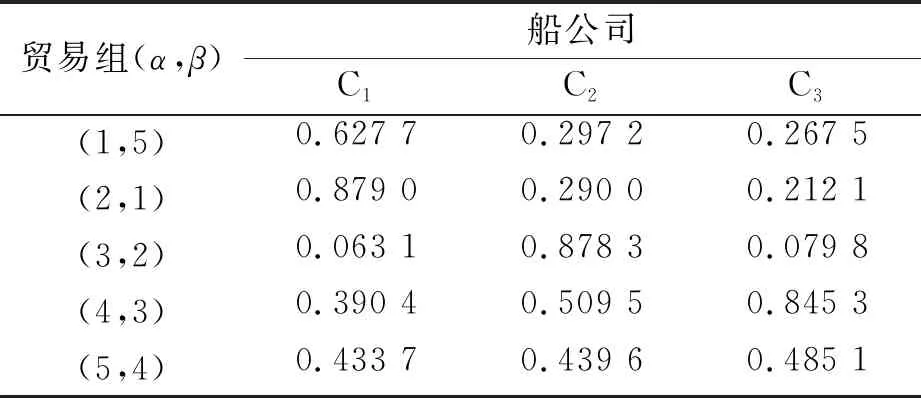
表9 发货人、收货人与船公司的整体满意度

将表9改写为指派问题中的满意度矩阵C,利用前文设计的模型算法,对满意度矩阵进行5次变换,便可得到最优匹配矩阵M:

用图示法表达即为:F1↔C3↔S5、F2↔C1↔S1、F3↔C1↔S2、F4↔C3↔S3、F5↔C3↔S4。匹配结果表明船公司C1承担了两项海运任务,船公司C3承担了三项海运任务,船公司C2不承担运输任务,符合模型的特征和现实情况。同时,经过验证计算,在目标函数权重系数不变时,其他匹配方案上的三方主体满意度都会低于现有的匹配方案。因此,本文在同时考虑了三方匹配主体满意度的基础上构建的模型,所求得的匹配结果即为全局最优方案。

总之,基于三方匹配主体的利益需求,建立了多边多目标的海运服务匹配模型,通过将模型转化为经典的指派问题,受匈牙利解法的启发,设计出可通过有限次迭代即可获得最优解的求解算法,成功为发货人和收货人匹配到了满足各方要求的船公司,进而促进国际集装箱海运服务高效运作。

4.3 匹配主体权重系数敏感分析

在模型求解过程中,为保证三方匹配主体的公平性,在将多目标转化为单目标的过程中,三方主体的权重系数均相等。为探索不同权重系数对于最优匹配方案的影响,分别对三方匹配主体的权重系数设置了24组不同的方案。利用前文的模型计算,得到三方主体在不同权重系数下的最优匹配方案,如表10所示。

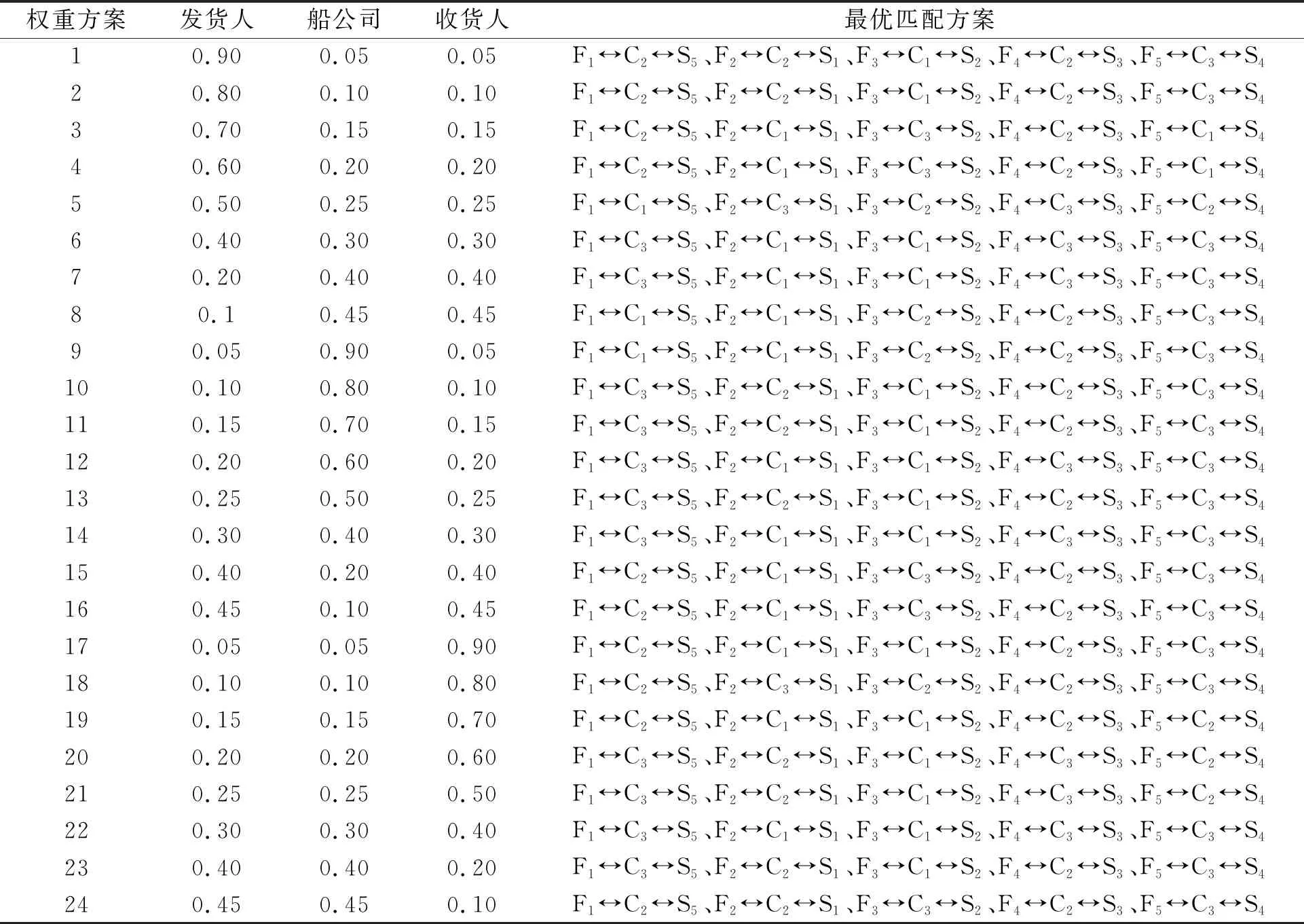
表10 三方匹配主体在不同权重系数下的最优匹配方案

从4组不同权重系数配置下产生的最优匹配方案来看,不同的主体权重对于匹配结果有较大影响,但是在三方的权重系数越接近时,最优匹配方案稳定在权重系数等于1/3时。因此,从管理者的角度分析,匹配平台应该结合实际注重不同集装箱海运匹配主体的市场地位,以保证匹配的公平性和方案的最优性。

5 结论

(1)构建了以发货人、船公司和收货人为主体的多指标多边多目标的匹配模型。将匹配指标划分为效益型指标和成本型指标,通过集结不同匹配主体在不同类型指标下的满意度,在表达不同主体视角下的整体满意度中创新性地采用连乘符号连接前后段匹配环节的满意度,刻画出国际海运服务选择的特点。

(2)在模型求解方面,通过将多边多目标的匹配问题转化为非标准的指派问题,借鉴匈牙利算法的思想设计出新颖且快捷有效的求解方法。相较于传统的匈牙利算法,该解法无需将行和列的数量转化为相等的矩阵,减少了矩阵变换次数,从而提高运算效率。

(3)区别于传统的独立零元素的定义,该解法中允许行和列中存在多个零元素,更加符合海运匹配市场的现实需求。文中所研究的模型和求解算法在一定程度上能够为国际集装箱海运服务匹配平台的相关管理者提供决策依据。