薄壁筒零件切削振动声学特性与试验研究

田美霞,吕凯波,郭富强,胡世杰,李 臻,庞新宇

(太原理工大学 机械与运载工程学院,太原 030024)

薄壁筒类零件具有质量轻、结构紧凑等优点,广泛应用于航空航天、船舶和石油化工等领域。由于薄壁筒零件自身刚度较低,切削加工过程中,刀具与工件之间极易产生相对振动,诱发切削颤振,加工现场伴随有刺耳的噪声[1-3]。因此,深入研究薄壁筒类零件切削加工过程中的振动声学特性,分析振动声学响应与工件加工表面质量的内在关联,这将对薄壁筒类零件切削质量的在线监测与控制具有重要的指导意义。

Mehdi等[4]分析了不同材料、几何形状和切削参数对薄壁筒工件振动响应特性的影响,并指出不同切削位置处工件表面形貌不同。Sun等[5]基于Sanders壳体理论,采用傅里叶级数展开法,研究不同边界条件下旋转薄壁圆柱体的固有特性。Gerasimenko 等[6]利用解析法预测薄壁圆柱零件的切削稳定性极限,切削试验表明颤振频率通常与零件壳体模态频率相接近。仇健[7]提出一种基于动态切削力和刀具动态位移时域仿真的车削颤振判稳方法。Lu等[8]建立了考虑切削位置变化的细长轴车削颤振模型,绘制出单次走刀的颤振稳定性图,并指出颤振加工表面呈沟槽形状。巫永琳[9]考虑弯板刀具的静态偏移和振动等因素,仿真结合试验得出车削参数对薄壁筒内腔表面粗糙度的影响规律。刘一沛等[10]针对薄壁筒工件车削颤振问题,采用数值仿真和试验测试相结合的方法,研究了切削过程中时变工件厚度和切削位置对薄壁筒振动特性的影响规律。

针对机床切削噪声,也有学者开展了相关研究。相比于结构振动、切削力等信号,声音信号往往包含了更为丰富的时、频域信息[11-12]。吴雅等[13-14]通过机床噪声试验发现,切削噪声与动态切削力具有较强的相关性,切削噪声频率与工艺系统某一阶薄弱模态相关。郭鹏[15]总结了车削加工过程中声音信号的构成,分析了主轴转速、切削深度、进给量、刀具主偏角等对切削噪声的影响。Cao等[16]对声压信号进行同步压缩变化,并利用3σ准则实现了铣削加工过程中的颤振监测。吕凯波等[17]采用小波包对车削过程中的声压信号进行实时分解,建立了基于能量峭度指标的早期切削颤振预警技术。

总体而言,切削过程中薄壁筒工件的振动行为要比轴类零件复杂得多,当前车削噪声方面的研究多以轴类零件为主,且鲜有文献关注切削噪声响应特性与加工表面形貌特征的映射关系。本文针对薄壁筒工件车削颤振问题,研究其切削振动声学特性及其对工件表面形貌的影响规律。首先通过理论建模与数值仿真得到不同特征频率下工件表面声压值、周围空间的声压级变化情况;而后开展薄壁筒工件车削试验,研究分析基于实测声音信号的工件表面形貌重构。

1 薄壁筒切削振动声学特性

1.1 薄壁筒工件振动模型

切削过程中,由于动态切削力的作用,工件-刀具工艺系统发生振动,这种结构振动带动了毗邻的弹性空气媒介分子的振动,依靠空气的惯性和弹性性质,空气分子的振动就以声波的形式向四周传播。

考虑到薄壁筒工件的柔度远大于刀具、机床结构的柔度,故以工件为唯一主振动体建立切削系统振动模型,如图1所示。在柱坐标Oxθz中,薄壁筒以角速度Ω绕机床主轴x轴旋转,图1中：L,H和R分别为薄壁筒的长度、厚度和中面半径;u(x,θ,t),v(x,θ,t)和w(x,θ,t)分别为中面上任意一点在轴向、周向和径向3个方向上的振动位移;Fx(x,θ,t),Fθ(x,θ,t)和Fz(x,θ,t)为中性面上一点的切削力F沿3个方向的分力;t为旋转时间。

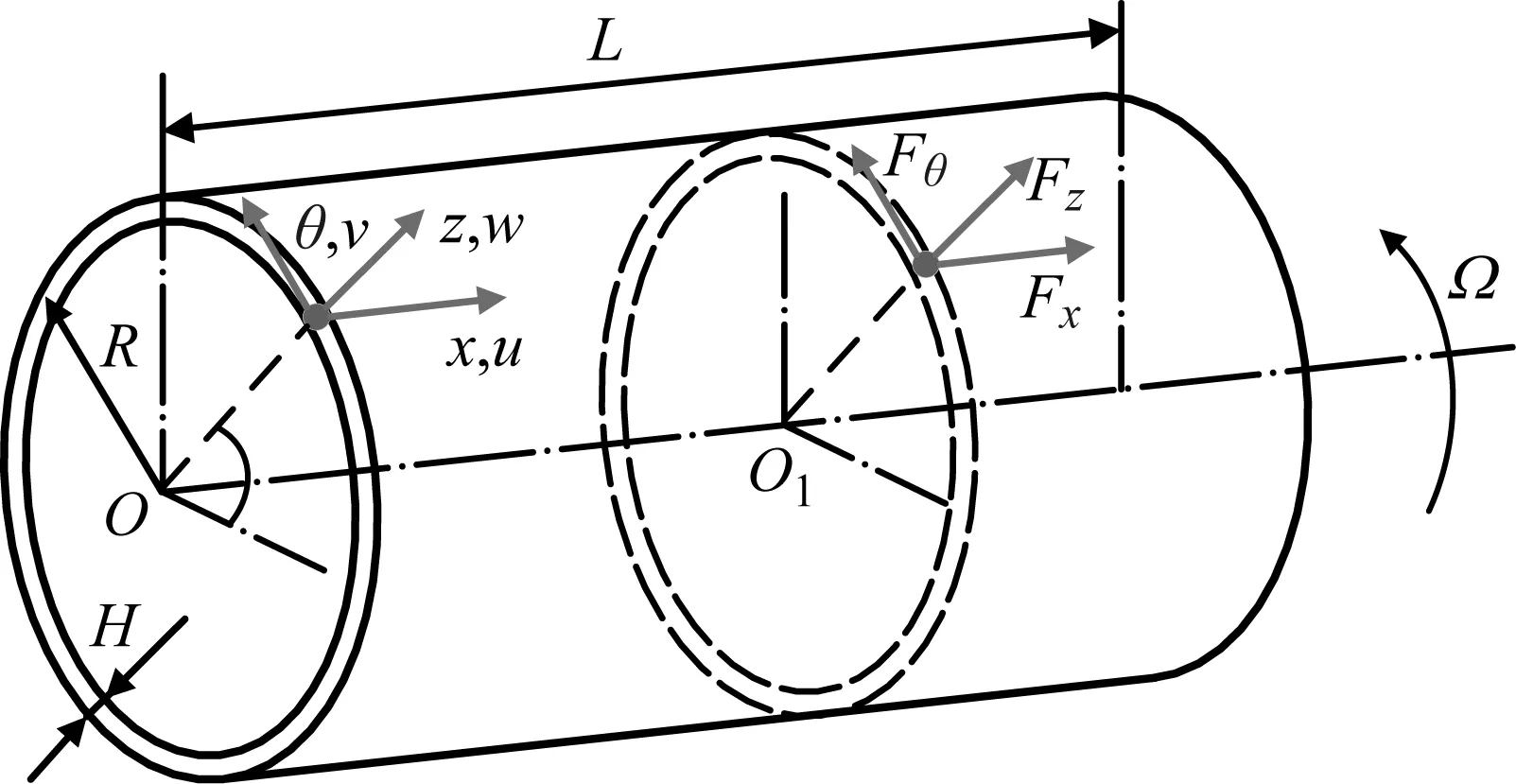
图1 旋转薄壁筒模型

基于Love壳体理论和Hamilton功能原理,考虑旋转薄壁筒的结构阻尼,建立其振动微分方程[18]

对于薄壁圆柱壳体,其模态振型由两部分组成,即轴向梁函数振型和周向花瓣状振型。依据分离变量法和振型叠加原理,壳体的振型函数可以由轴向梁函数和周向三角函数的组合形式来近似表示,其位移解可表示为

(4)

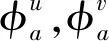
(5)

式中,cij(i,j=1,2,3)的具体表达式可参考文献[19]。根据式(5)存在唯一解的条件是系数行列式为零,可以得到旋转薄壁筒的固有频率

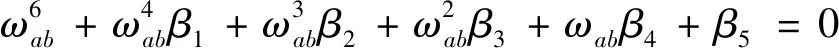
(6)

式中,βi(i=1,2,…,5)为待定系数,与工件的边界条件有关。

1.2 薄壁筒切削辐射声场模型

声波可以通过介质中的声压p、质点速度v以及密度变化量ρ′来描述和表征。薄壁筒振动过程中所产生的声音遵循声波方程,其表达式[20]为

(7)

在求解式(7)的过程中,可得到Helmholtz方程

∇2p+k2p=0

(8)

式中：k=ω/c0,k为声波数;ω为激励圆频率。

Helmholtz方程利用积分解来计算声场,在声学中应用十分广泛。Helmholtz积分方程将声场中任一点B的声压p(B)变成边界面S上许多小单元积分的和,其表达式为

(9)

式中：A为辐射声源;B为声场中的观测点;R=|B-A|,为点A和点B之间的距离;α与场点位置有关

(10)

求解式(9)需要用到边界条件,在边界面上表面声压p和法向振速vn存在以下关系

(11)

因此,根据式(1)～式(3)、式(11)建立起了薄壁筒动态切削力、切削振动和切削噪声三者之间的内在关系。在无限介质中,当振动结构表面的法向振动速度确定后,利用Helmholtz积分方程就可以确定给定表面声压和空间各点声压情况。

建立薄壁筒工件辐射声场模型,如图2所示。薄壁筒工件长度160 mm,厚度1.5 mm,内径111 mm,工件密度7 850 kg/m3,杨氏模量2×1011Pa,材料为结构钢。工件下端面添加固定约束,工件表面一点添加沿径向方向、幅值为10 N的激振力,激振力的频率范围取5～1 500 Hz,步长为5 Hz。在薄壁筒外侧建立边长为0.5 m的正方体,正方体的面边界选择平面波辐射,研究在此范围内声压分布情况。选择“声-固耦合”多物理场,将“压力声学”和“固体力学”接口相结合,进而将流体域中的声压变化与固体域中的结构变形联系起来。

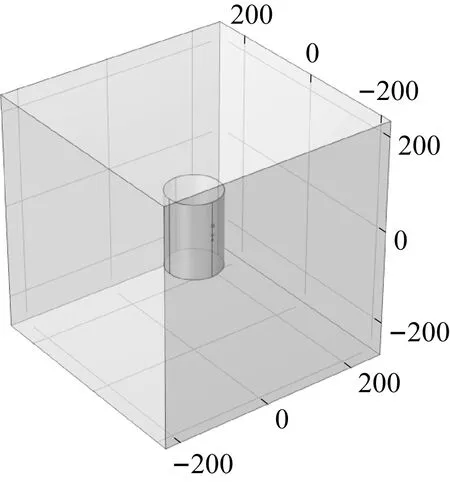
图2 薄壁筒工件辐射声场模型(mm)

1.3 薄壁筒振动声学特性仿真

由切削颤振理论可知,金属切削过程的振动特性、稳定性与工艺系统的薄弱模态密切相关,颤振频率往往略大于薄弱模态的固有频率。因此,在声学仿真之前,先对薄壁筒模型进行模态分析,得到工件的前两阶振型结果,如图3所示。可以发现,工件越靠近自由端,变形越大,说明该位置刚度较弱,越容易发生颤振。

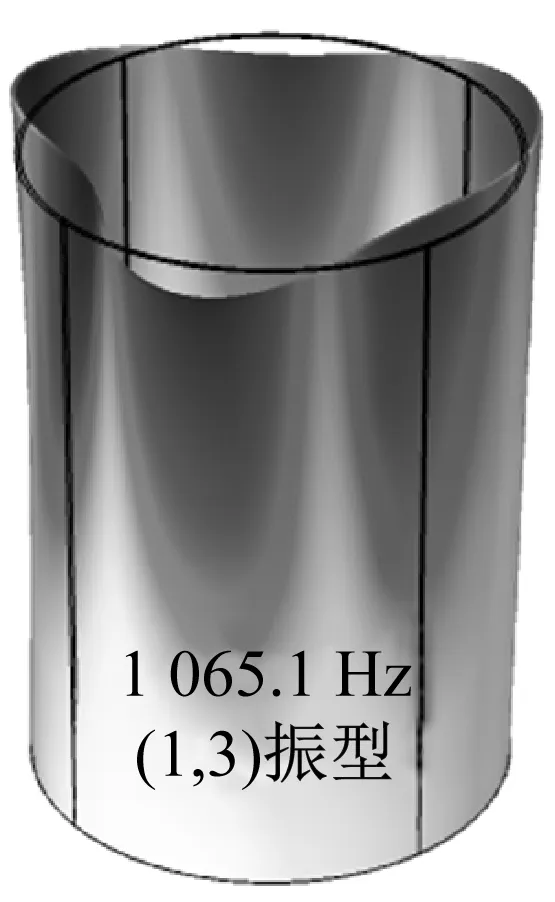
(a) (1,3)振型

选用自由四面体单元对辐射声场模型划分网格,开展有限元仿真。图4给出300 Hz外部激励下工件周围空间的声压级分布云图,可以看出：由刀具和工件一侧所引起的声压级值较大,而工件两端面则较小,并且距离工件越远,空间声压分布变弱。随着激振力频率的增大,工件表面的声压也越大,当激振频率与工件固有频率接近时,表面声压显著增大,如图5所示。

图4 在300 Hz激励下空间声压级云图

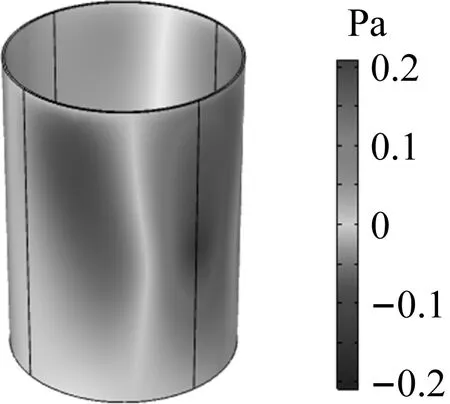
(a) 300 Hz

为了分析切削过程中工件-刀具接触点的实时改变对周围声场的影响,图6对比了工件表面不同激振点时空间测点(距离工件固定端80 mm)处的声压级变化情况。从图6可以看出：激振点越靠近自由端,测点处声压值越大;与此同时,不同测点呈现出一致的规律,声压峰值依次出现在工件的固有频率附近。

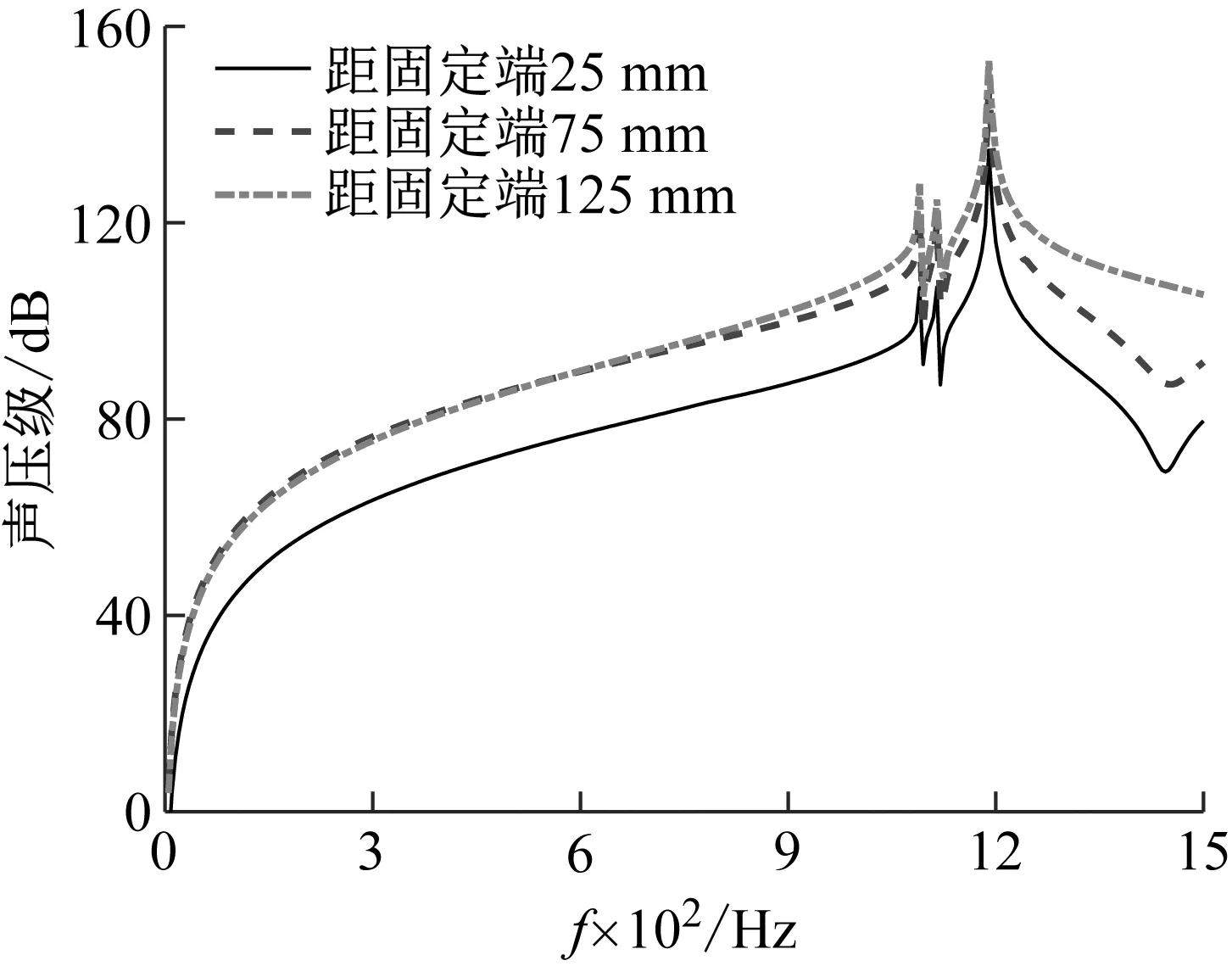
图6 不同激振位置下声压级对比图

2 切削试验与结果分析

2.1 试验台设计与搭建

为验证薄壁筒工件切削过程中振动声学特性及其与加工表面形貌的内在联系,在普通车床CA6140上开展车削试验,现场布置如图7所示。试验中选用刀杆型号为SDNCN2525M11,刀具型号为DCMT11T304,刀尖半径r=0.4 mm。选用的声音传感器型号为PCB 130F20,由支架固定放置于车床一侧;加速度传感器型号为PCB 352C34,贴附于刀具背面。选用两根材料为40钢的薄壁筒工件,工件一端由三爪卡盘夹持固定,另外一端自由,研究不同尺寸和切削参数下工件的振动声学特性和表面形貌特征。切削参数如表1所示。

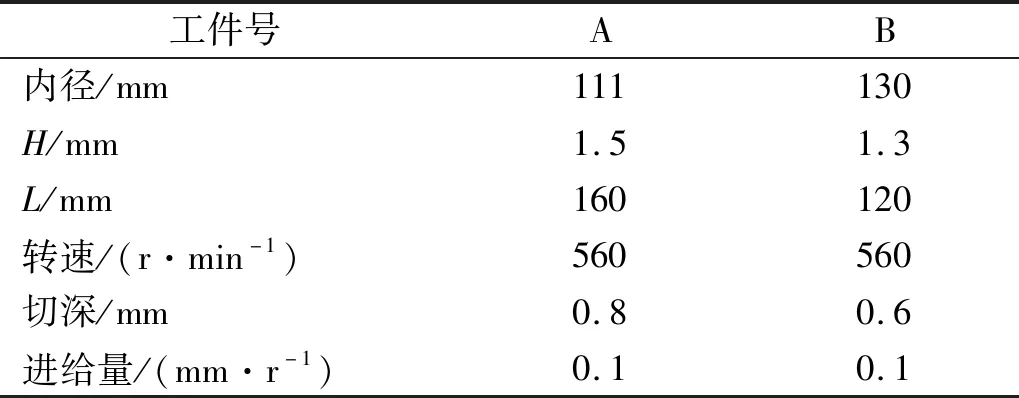
表1 切削参数

图7 车削试验台布置图

2.2 模态测试与分析

为得到工件的固有频率,对加工之后的工件进行锤击试验,敲击点在距离工件自由端15 mm处,采用加速度传感器拾取敲击点处的响应信号,得到工件的频率响应函数。图8给出工件A和工件B的频率响应函数试验结果。可以看出,工件A的前两阶固有频率分别为582.5 Hz和1 088 Hz。其中,第二阶频率与理论仿真结果(1,3)振型所对应的模态频率1 065.1 Hz相接近,但是第一阶频率582.5 Hz在仿真中并未出现,分析其原因,这可能是由于仿真分析中并未考虑机床主轴、卡盘等对工件模态的影响,这些组件对工件的弯曲梁模态有显著影响[21-22]。因此,推断582.5 Hz为主轴-卡盘-工件工艺系统的弯曲模态。工件B的前3阶模态频率分别为573.6 Hz,1 058 Hz和1 273 Hz。

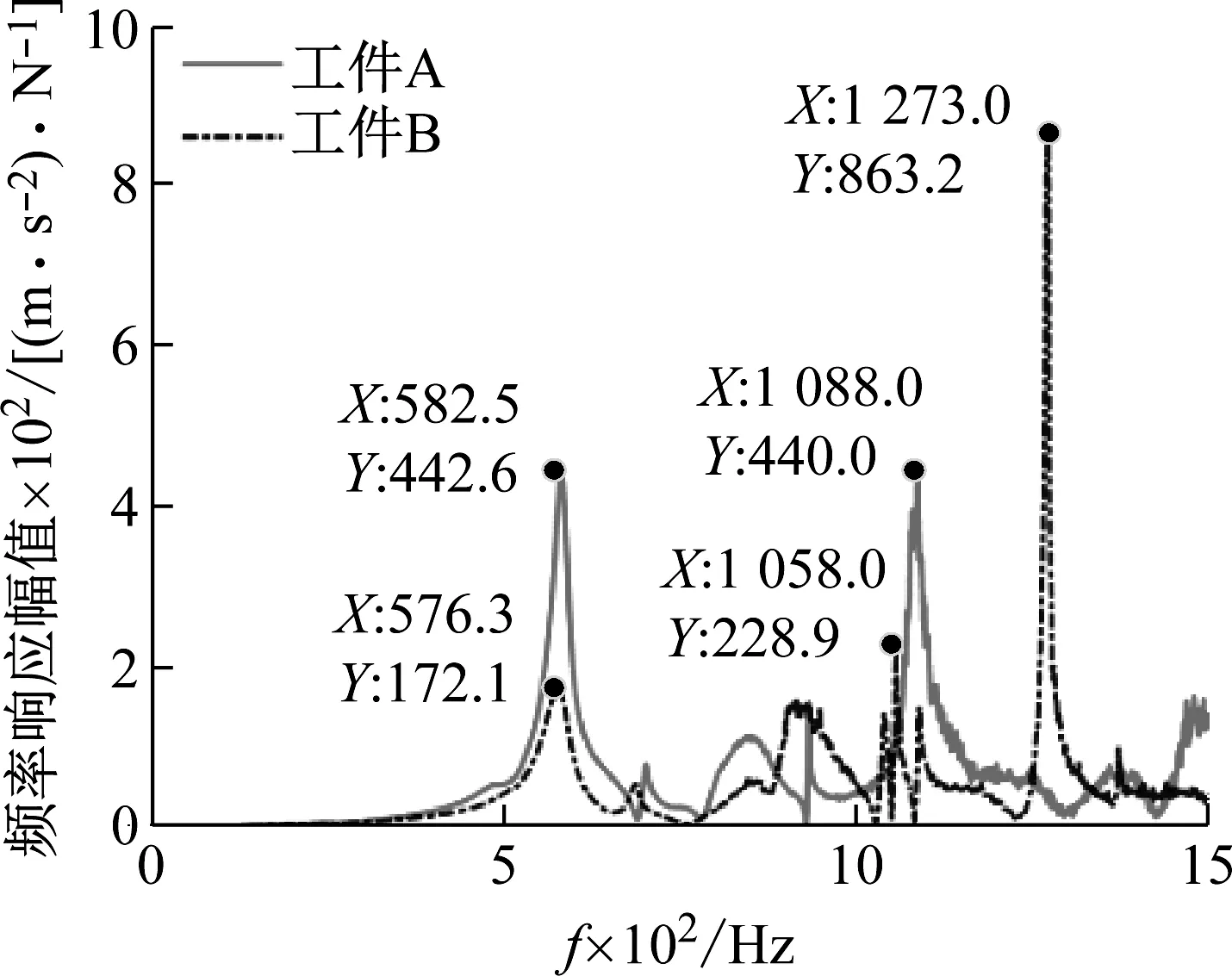
图8 工件A和B的频率响应函数

2.3 信号分析与形貌重构

在切削过程中,开始阶段薄壁筒工件加工状态平稳;当切削到工件轴向某一位置时,现场开始出现刺耳的切削噪声,且噪声呈现周期性规律变化,声音强度重复经历从增强到衰弱,再增强到再衰弱,直至加工结束。图9为工件A和工件B在整个切削过程中的声压信号对比图。可以看出,当稳定切削时,声压幅值较小,当颤振发生后,声压信号幅值显著增大。

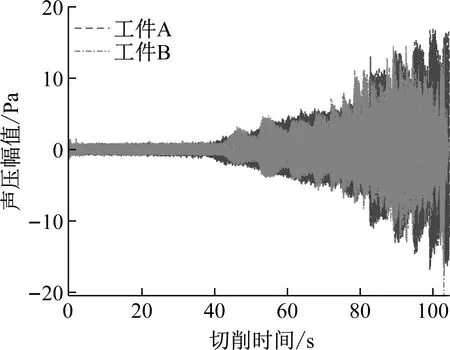
图9 工件A和工件B切削声压信号

图10为工件A切削完成之后的表面形貌图。根据其表面特征可以分为3个区域：区域一是平稳加工阶段,工件表面光滑;区域二是轻微颤振阶段,工件表面呈现规律的斜条纹图案;区域三是严重颤振阶段,工件表面呈现规律的抛物线图案。

图10 工件A表面形貌图

对采集到的声压信号做短时傅里叶变换,以获得不同时刻的声压频谱信息。图11为工件A加工过程中声压信号时频分析结果,可以发现,工件在区域二中的颤振频率为621.5 Hz,略高于图8中的第一阶固有频率582.5 Hz,且颤振频率基本保持不变;对于区域三,颤振频率跳变为1 096 Hz及其倍频成份为主,接近于工件的第二阶固有频率1 088 Hz,且频率有逐渐下降的趋势。这说明工件在不同切削位置处产生不同的声学响应和表面形貌特征,这可能与加工过程中工件主振频率的变化有关。

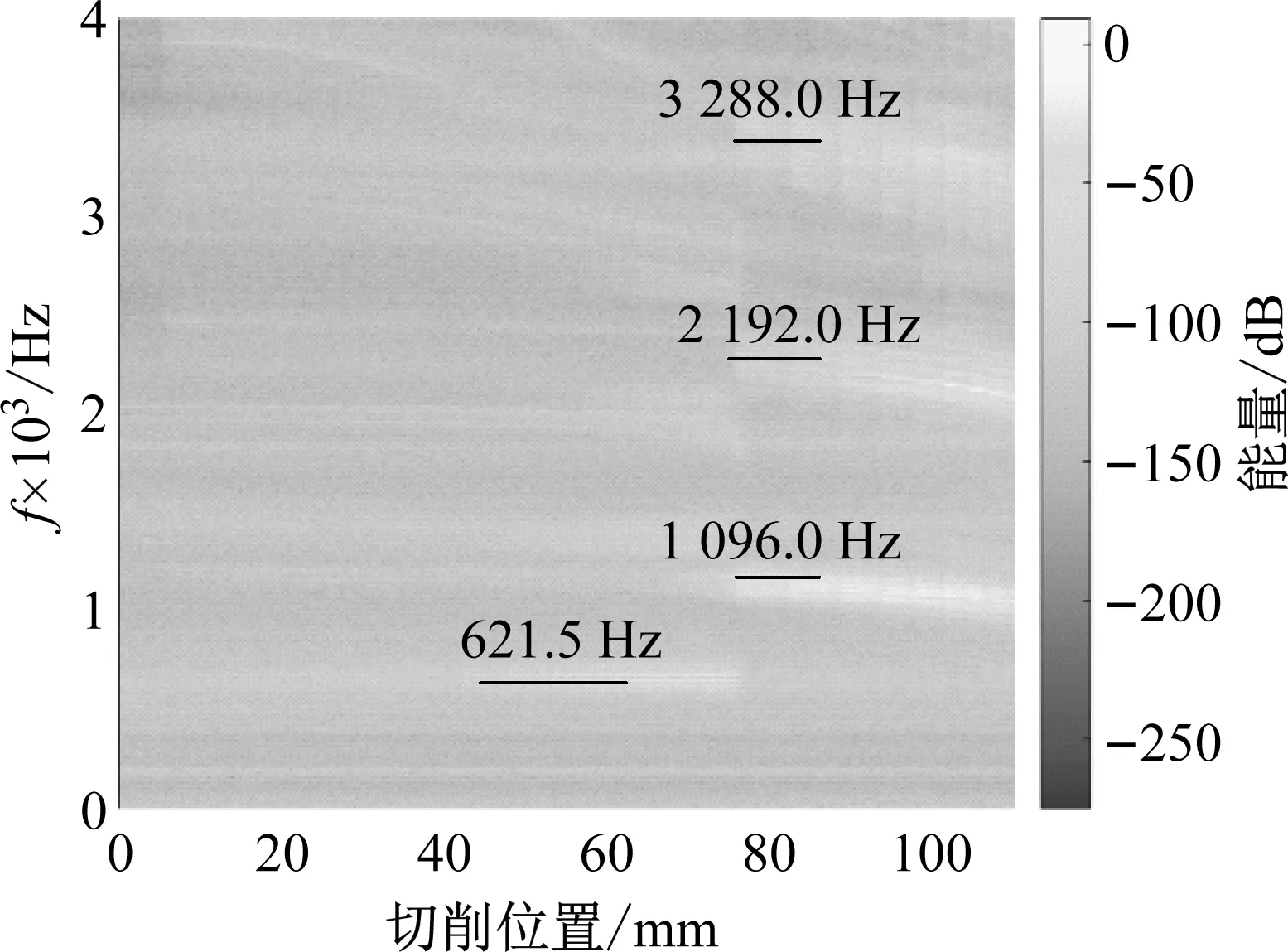
图11 工件A的声压信号时频谱图

图12和图13为基于原始声压信号的工件表面形貌展开图。其展开原理为：将采集到的每一个声压信号与切削过程中实时变化的切削点处的振动一一对应,轴向以进给量为间隔,周向以采样周期为间隔,将信号数据点依次存储在工件表面切削点的相应位置,由此得到工件二维形貌展开图。可以看出,声音信号与工件表面形貌之间存在一定的映射关系。

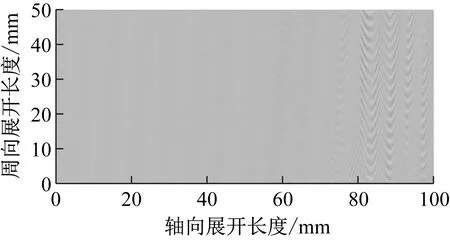
图12 基于原始声压信号的工件A表面形貌展开图

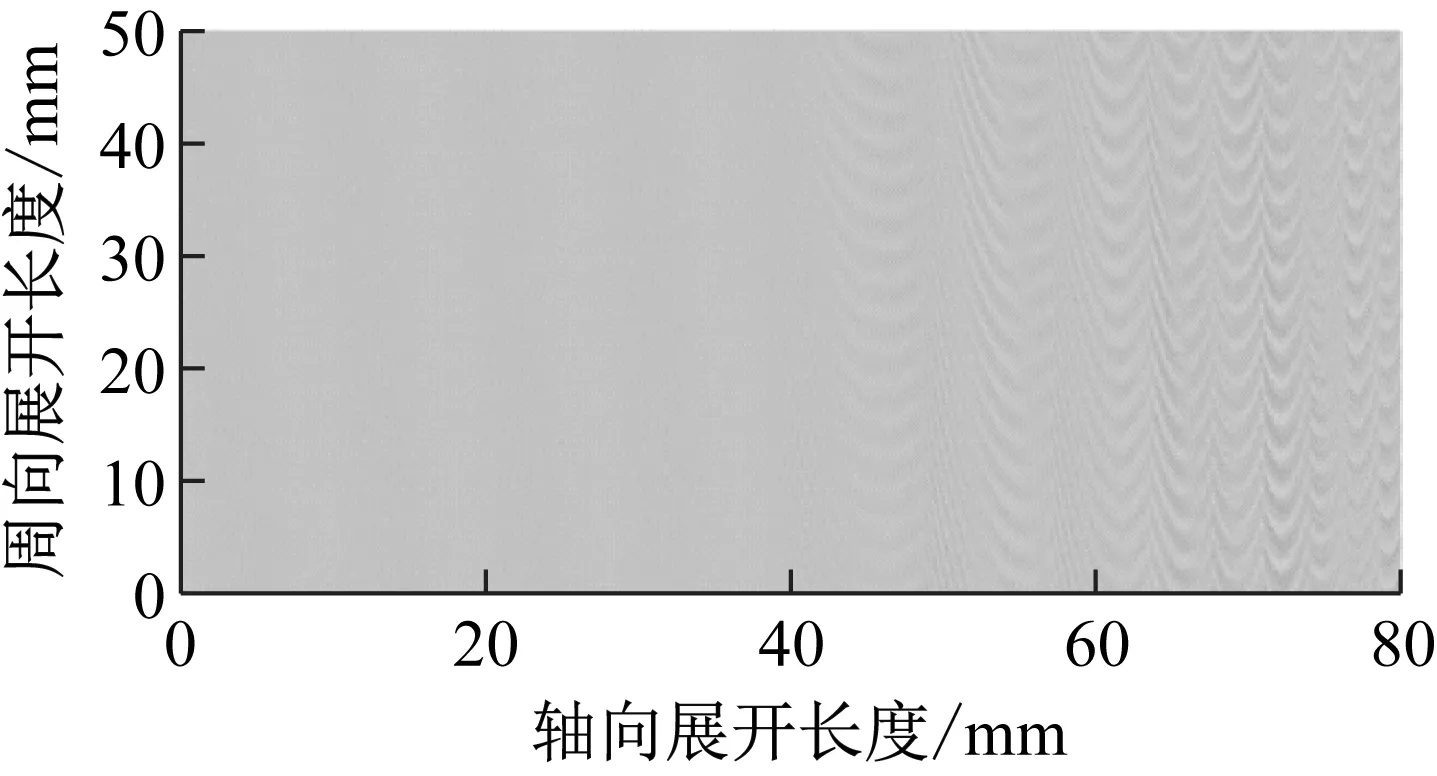
图13 基于原始声压信号的工件B表面形貌展开图

切削过程中采集到的声压信号不可避免存在噪声的干扰,提取切削路径上声压信号主振动频率的变化特征,结合被加工工件的几何尺寸和切削参数,重构获得薄壁筒切削加工表面形貌,如图14所示。从图14可以看出,在轴向0～40 mm内重构表面光滑平整,40～78 mm内为有规律的斜条纹形貌,78～100 mm内是开口向上的抛物线,且相邻两组抛物线之间的距离越来越小,这与工件A实际表面形貌(见图10)具有一致性。

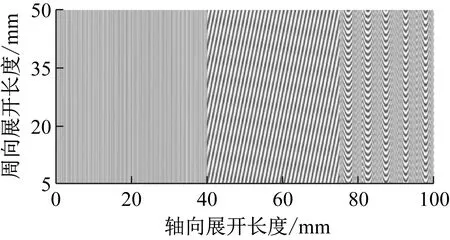
图14 基于特征频率提取的工件A表面形貌重构图

对工件B加工过程中的声压信号进行类似的分析,结果如图15所示。对比工件A可见,在不同的切削参数和工件尺寸作用下,薄壁筒零件切削振动声学响应及其加工表面形貌也会不同;与工件A的切削颤振不同,工件B并未出现颤振频率跳变现象,颤振频率以1 275 Hz及其倍频为主,这与模态测试结果的第三阶固有频率1 273 Hz相近。提取声压信号的特征频率,重构后的表面形貌与工件实际表面相似,轴向0～44 mm区间为平滑表面,44～80 mm为抛物线状表面形貌,且相邻两组抛物线之间的距离逐渐减小。

(a) 表面形貌图

综上,利用声音信号重构的表面形貌与工件实际表面形貌基本吻合,说明声固耦合振动作用下,工件切削噪声响应特性与加工表面形貌特征存在着映射关系,这对基于声压信号的薄壁筒类零件切削质量在线监控具有指导意义。

3 结 论

(1) 建立薄壁筒工件的声固耦合模型,利用动态切削力、切削振动和切削噪声三者之间的内在关系,数值仿真获得不同激振频率下工件表面、周围空间的声压分布情况。

(2) 分析获得薄壁筒切削系统从稳定到失稳状态下切削噪声信号的时频域特征,对比建立切削过程中声学响应信号特性与工件表面不同位置处形貌特征的对应关系。

(3) 基于切削噪声信号,提取切削历程中振动频率的变化特征,结合被加工工件的几何尺寸和切削参数,重构获得薄壁筒切削加工表面形貌,与实测表面结构具有一致性。