电池储能跟踪发电计划及平抑风电波动的多目标优化控制

罗隆福 ，庞涛 †，李勇 ，刘晓丹 ，田野 ，余璇

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.国网湖南省电力有限公司经济技术研究院，湖南 长沙 410007；3.能源互联网供需运营湖南省重点实验室，湖南 长沙 410007）

为应对日益严峻的环境压力与我国能源结构调整的战略需求，我国提出大力发展可再生能源.根据2021 年中国环境统计年鉴，风电装机容量从2015 年末的13 075万 kW 增长到2020年末的28 165万 kW，可见风电装机容量在我国有显著提升［1］.风力发电受天气的影响，有很强的波动性和随机性.因此大规模风电并网给电力系统带来了安全稳定方面的不利影响.

为降低风电并网对电网的冲击，需要对风电出力进行调控.储能技术可有效提升电网对新能源的消纳能力，成为解决风电并网问题的关键技术［2］.关于提升风电并网的稳定性，学者们主要聚焦于两方面的问题，一个是平抑风电功率波动，另一个是降低风电并网功率与发电计划的偏差.

平抑风电功率波动方面，张坤等［3］采用一阶低通滤波获取风电功率高频部分，用储能对高频部分进行补偿.欧阳曾恺［4］在此基础上进一步讨论了判别步长对控制效果和储能荷电状态（State of Charge，SOC）的影响.苏强强［5］提出基于SOC 的变时间常数的平滑控制策略.然而以上方法灵敏度和平稳度难以兼顾，难以适应风速骤变的情况，容易造成储能过补偿和欠补偿.为了减少电池充放电状态转换次数，从而减少电池寿命损耗，Yao 等［6］提出使用双电池储能系统解决风电并网功率波动问题，使两组储能分别处于充电和放电状态，待满充满放后再同步进行切换充放电状态.但实际上风电正向波动和负向波动的能量不总是均衡的，会使其中一组储能先达到满充满放状态，而使另一组储能被动切换.因此有学者提出了新的双储能系统控制策略平抑风电波动，并以优化储能SOC 或运行成本为目标［7-11］.张新松等［12］对双储能系统平抑风电的运行策略做了归纳并进行比较分析.帅挽澜等［13］提出一种综合能源系统协同方案，提高风电消纳能力.臧紫坤等［14］提出了一种降低弃能率的风光火储调度方案.为适应不同时间尺度的风电波动平抑需求，不少学者利用离散傅里叶变换、经验模态分解及变分模态分解等频域分析法分解风电，使用功率型和能量型储能组成混合储能系统来平抑不同频段的功率波动［15-17］.而以上频域方法的端点效应是影响控制性能不容忽视的因素.

降低风电并网功率与发电计划的偏差方面，李滨等［18］针对大型风电场提出了评价标准.柴炜等［19］提出了基于风功率超短期预测的储能策略，但其效果取决于预测的准确度.同时，模糊理论也应用于降低误差，根据SOC 对储能功率进行调整［20］.Moghaddam 等［21］使用预测控制器提升高风能渗透率下的并网功率准确率.柴炜等［22］考虑了控制步长和控制周期对储能寿命和跟踪发电计划能力的影响，提出了储能的变步长优化控制策略.罗煜等［23］提出一种储能辅助跟踪风电计划的实时滚动优化控制策略.Li等［24］将频域方法和混合储能技术引入跟踪发电计划的应用场景.Zhang 等［25］则将双电池系统集成到风电场以降低并网功率误差，并比较了同步和异步状态交换策略的技术性和经济性.Liu等［26］以抽水蓄能电站为主，以电池储能为辅，来优化风储电站发电计划以及实时降低发电误差.

上述文献基本将平抑风电波动和补偿风力发电误差分开控制，而实际上这两者是风电并网运行需要同时满足的需求.有学者兼顾了以上两者，但主要聚焦于储能的最优配置而非控制［27］.

本文提出了一种应用于电池储能系统（Battery Energy Storage System，BESS）辅助风电场联合发电的多目标优化控制策略.首先，分析“三站合一”风储电站的功率关系，并建立了合理评价风储并网功率的评价指标；其次，兼顾风电出力平抑和补偿风电误差，同时考虑电池储能系统SOC 和充放电电量的优化，建立了多目标优化模型；之后，利用多目标智能算法和模糊综合评价方法进行决策，确定储能系统的实时功率指令，以在满足风电并网需求的同时优化电池SOC 和延长电池寿命；最后，以湖南省某风储电站的实际数据搭建模型，验证本文策略的有效性.

1 “三站合一”风储电站

1.1 风储电站拓扑结构

湖南省某风储电站采用的“三站合一”拓扑结构如图1 所示.装机容量为50 MW 的双馈风机群经汇集线接入升压站主变35 kV 侧，配置容量为10 MW/20 MW·h的储能站也同时接入该35 kV侧.为解决风电储能电站的电能质量问题，升压站采用感应滤波技术［28］，配置的无功补偿装置及滤波器组经特殊设计额定电压为35 kV的感应滤波绕组接入升压站.该风电站因位于丘陵山区，各风机安装范围广，场站测风塔无法准确代表各个风机实时风速，且天气条件反复变化，数值天气预测的参数误差较大，致使日前风功率预测效果不理想.电力系统无法对该风电站的输出功率进行有效规划和调度，且该接入电网偏远薄弱，易影响区域电网稳定及安全.为此配置储能站对随机性强的风功率进行功率平抑，增加风电站输出功率的稳定性及可调控性.

图1 风储联合发电系统结构图Fig.1 Structure of wind storage combined power generation system

1.2 风储联合发电特性

风储电站并网功率、双馈风机群输出风功率及储能站输出功率的关系为：

式中：Pwind、Pbess和Pout分别为风电实际功率、电池储能系统功率和总输出功率，设定电池储能系统放电时功率为正.

储能站的主要作用在于提升风储电站并网功率的可控性和合格率，即并网功率能够跟踪上级调度下发的发电计划及平抑风功率可能存在的频繁波动，所以储能站的输出功率为：

式中：Pbess-1、Pbess-2分别为跟踪发电计划、平抑风功率波动所需的储能站补偿功率；Pplan为发电计划值；Pc为风电场的开机容量，开机容量即风电场某时刻实际运行风机的总容量，一般风电场所有风机都运行，故通常开机容量和装机容量相等；ε1为发电计划曲线所允许的误差；Ptag为符合风功率并网要求的并网功率目标值.

储能电站的荷电状态及输出功率存在以下关系：

式中：SOC（t）、SOC（t+Δt）分别为实时及下一时刻的储能站等效荷电状态值；Crate为储能站的额定容量；ρ为储能站的自放电率；Pbatt为储能电池的等效功率；ηchar、ηdis分别为储能变流器的充电和放电效率；Fchar、Fdis分别为储能站充电、放电标志.

图2 为储能平抑风电功率和辅助风电场跟踪发电计划的控制流程图.

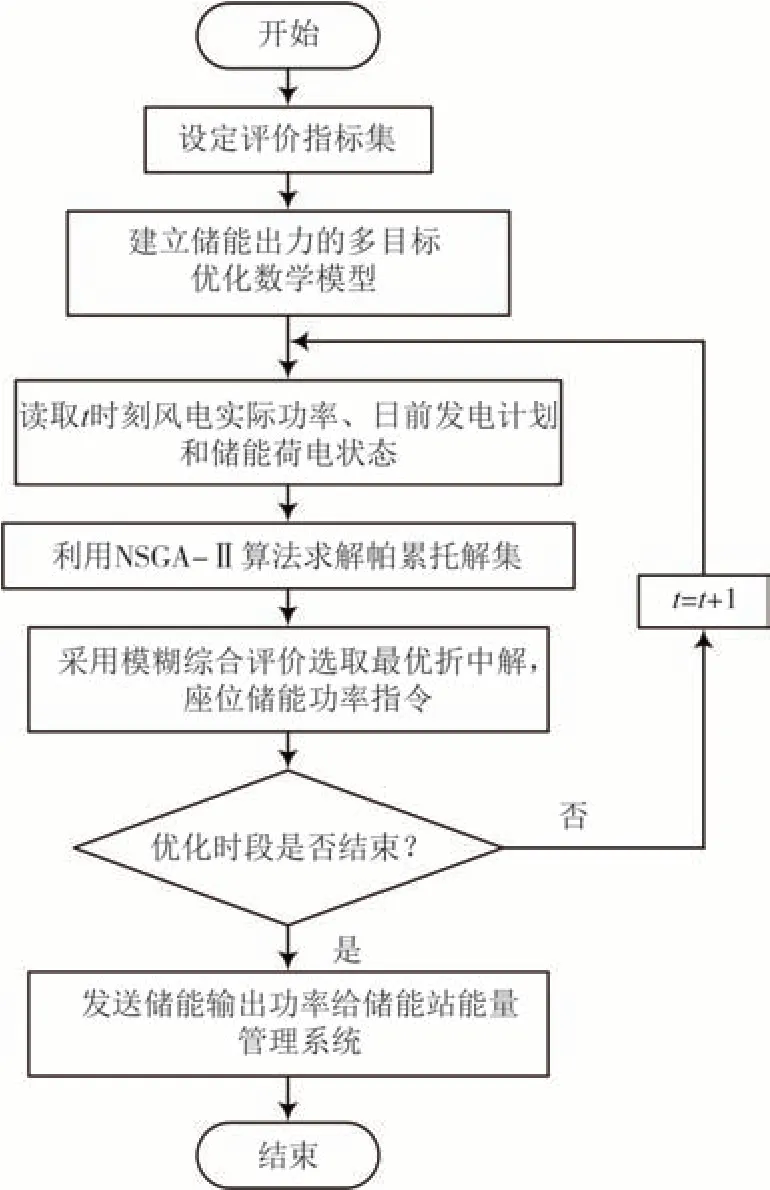
图2 储能系统有功功率控制流程图Fig.2 Active power control flow chart of energy storage system

2 风储联合发电的多目标优化模型

2.1 评价指标

为了合理地评价风储电站的并网功率，需要建立合适的评价指标来评判储能站有功功率输出的正确性及合理性.本文参考了风力发电和储能充放电的相关标准和要求，建立评价文中控制策略的评价指标.储能站的首要目标为增强风储电站并网功率的可调度性，即跟踪发电计划曲线：

式中：γplan（t）为t时刻风储电站并网功率的准确率，表明考核点风储并网功率与发电计划的准确程度；φplan为考核总时段的并网功率的跟踪准确率，用以评估全时段并网功率跟踪发电计划的准确程度；N为总评价时间段内的评价点总数.

为了评判评价时段内并网功率实时准确率的合格情况，建立并网功率调度合格率为：

式中：Bplan为总评价时间段内的并网功率调度合格率，旨在评估并网功率符合调度要求的总体情况；Fplan(γplan(t))为t时刻功率调度合格的标志.

根据《风电场接入电力系统技术规定 第1部分：陆上风电》（GB/T 19963.1—2021），对于并网的风功率的波动进行了要求和限制，主要分为10 min 有功功率变化最大限制和1 min 有功功率变化最大限制.此外，储能电站同时也要兼顾对风功率频繁波动进行补偿使其符合该国标中风电站并网的要求，建立并网功率波动合格率为：

式中：γflu（t）为Tflu时间尺度内的功率波动率；φflu为功率平滑度，以Tflu时间段为基本单位，是总评价时间段内的功率波动率的平均值，旨在评估总时间段内功率曲线的平滑程度，数值越小表征功率曲线越平滑；Bflu为总评价时间段内的并网功率波动合格率，旨在评估并网功率符合风功率波动要求的程度；ε2为Tflu时间尺度内的有功功率波动率限值；Sc为风电场装机容量.

储能电池的使用寿命是储能应用不可避免要考虑的问题，如何延长储能电池的使用寿命也是相关领域所关注研究的重点和难点.在尽可能满足跟踪发电计划及平抑功率波动的基础上，合理规划储能系统的功率输出，需要对储能站的功率输出进行评价.一般用循环充放电的次数表示储能的寿命情况，但在风储应用场景下，储能充放电是不具周期性和规律性的，此时可根据储能当前的累积吞吐电量估计储能寿命［22］.如式（11）所示，本文在累积吞吐电量的基础上，进一步细分出充电电量和放电电量，以便于分析储能充电和放电情况.

式中：Echar、Edis和Esum分别表示总充电电量、总放电电量和累积吞吐电量；T为储能控制步长.

2.2 目标函数建立

建立与并网功率的跟踪准确率相对应的目标函数：

式中：a1和b1是函数的常量参数.分析可知，当并网功率偏离发电计划允许度时，根据偏离程度大小，目标函数f1将会增大.故目标函数f1的值越小，表示并网功率越能满足发电计划的要求，表明其具有良好的可调度性.

建立与并网功率波动合格率相对应的目标函数：

式中：a2和b2是函数的常量参数.当并网功率的波动幅度不满足上述国标的要求时，目标函数f2将会增大.故f2的值越小，表示并网功率的波动越符合上述国标的波动要求，表明其具有良好的平滑性.

建立与单次充放电电量相对应的目标函数如式（14）所示：

f3代表储能在单步控制中的充放电电量，其值越小，表示在控制步长T内充放电造成的储能寿命损耗越小.

在储能站和风机群的并网功率能满足上述跟踪发电计划及平抑功率波动的基础上，为了减小储能电池寿命的不必要损耗，避免储能电池使用不当造成的安全隐患及浪费，应避免储能电池出现过充过放现象.同时应尽可能地使储能电池的SOC 维持在合理范围.为了清晰地描述储能电池SOC 状态，对储能电池SOC进行分区，如图3所示.

图3 储能SOC分区图Fig.3 SOC zoning diagram of energy storage

储能电池的SOC依次分为过放区Z1∈［0，SOCmin］、放电警戒区Z2∈［SOCmin，SOCa］、充电倾向区Z3∈［SOCa，SOCb］、放电倾向区Z4∈［SOCb，SOCc］、充电警戒区Z5∈［SOCc，SOCmax］及过充区Z6∈［SOCmax，1］.建立与储能电池总充放电电量相对应的目标函数如式（15）～式（17）所示.

储能电池SOC 优化的目标函数f4分为充电状态和放电状态两部分，在SOC 的5 个对应分区中分别予以评判.当储能电池的SOC 逐步偏离正常区时，f4会逐渐增大，增大幅度与储能电池的SOC 偏离程度正相关.故，目标函数f4的值越小，表示储能电池的SOC 长期处于正常区域，表明充放电电量在可控合理范围内，能极大地延长储能电池的使用寿命.

2.3 多目标优化模型

根据上述目标函数，结合多目标优化理论，建立储能电站输出功率多目标优化模型：

本文以式（1）、式（2）为风储联合发电系统功率约束，式（3）～式（5）为储能容量和荷电状态约束，式（19）为储能功率约束.

式中：Pdismax和Pcharmax分别为储能放电和充电的最大功率.

3 基于模糊综合评价的多目标优化

3.1 NSGA-Ⅱ算法求解非劣解

第2代非支配排序遗传算法（Nondominated Sorting Genetic Algorithms，NSGA-Ⅱ）是Srinivas 和Deb改进过的，适用于多目标优化的遗传算法［29］.

针对第2 节中的优化模型，使用NSGA-Ⅱ算法进行求解，得到非劣解集合，其流程图如图4 所示，简述如下：

图4 非劣解集求解流程图Fig.4 Flow chart for solving non-inferior solution set

1）导入各采样时刻的风电有功功率、储能有功功率、风电预测功率、电池状态等，进行参数初始化，通过随机方式在解空间内产生种群.

2）对种群中每个个体进行非支配排序，找出其中所有非劣解并划分帕累托等级，随后将这些个体按照帕累托等级进行排序.

3）计算拥挤度.传统NSGA-Ⅱ算法将位于约束边界的拥挤度设为无穷大，对非边界的个体，利用相邻个体的目标函数值计算拥挤度.该方法不适合帕累托前沿出现离散点的情况.而本文所考虑的优化问题目标函数值存在不连续情况.为了避免帕累托前沿不连续时陷入局部，本文将解集中目标函数值相等时的拥挤度设为0.

4）二进制竞赛选择.以拥挤度和帕累托等级作为判据，选择其中较优的个体.

5）采用模拟二进制交叉和多项式变异方式诞生子代.迭代完成后，最终的种群即非劣解集.

3.2 基于模糊综合评价的决策方法

计算出储能出力优化模型的非劣解集后，基于图5 所示的模糊决策方法，从解集中确定一个最优折中解作为储能在该优化时刻的出力.其流程如下：

图5 综合评价模型与流程Fig.5 Comprehensive evaluation model and process

1）本文将优化模型的目标函数作为评价指标集，并根据指标值对系统的影响构建风储优化控制的评判集V=［NB NS ZO PS PB］.

2）确定指标集中各指标对评价等级的影响权重.本文研究的优化问题具有明显的侧重点，需要专家根据经验进行主观判断.因此本文采用主观法中常用的层次分析法确定其权重，构造判断矩阵A，并求得权重w，对应各目标函数对决策的影响程度.

3）对指标集数据进行预处理，计算指标对应各评价等级的隶属度并建立隶属度矩阵R.由于本文中指标集元素是4 个，评判集元素是5 个，故隶属度矩阵R为4 行5 列矩阵.其中，评判集V中5 个等级的隶属度函数如图6所示.

图6 评判集隶属度Fig.6 Membership of the evaluation set

4）如式（20）所示，采用对权重敏感的加权平均算子，计算综合隶属度向量B，文中评判集有5 个等级，故B=[b1，b2，b3，b4，b5]，其表示储能出力方案在评判集中各等级所占的隶属度.

式中：bj为隶属度向量B的第j元素；rij为隶属度矩阵R中元素.

5）为客观比较各个解的优劣，对应评判集V建立等级分数向量S，并依照式（21）计算综合评分值G，同时计算储能不出力的综合评分，选择综合评分最高的解作为优化控制的指令输出.

式中：sj为评分集S的第j元素.

4 算例验证

以图1 所示风储联合发电系统为例，该风电场的装机容量为50 MW，储能站容量配置为10 MW/20 MW·h.实测某24 h 的发电计划和风电实际并网发电数据进行验证，控制步长与数据采样周期为5 min，优化周期内共计288个点.本文设定的发电准确率和10 min波动率合格要求以及其他控制参数如表1所示.

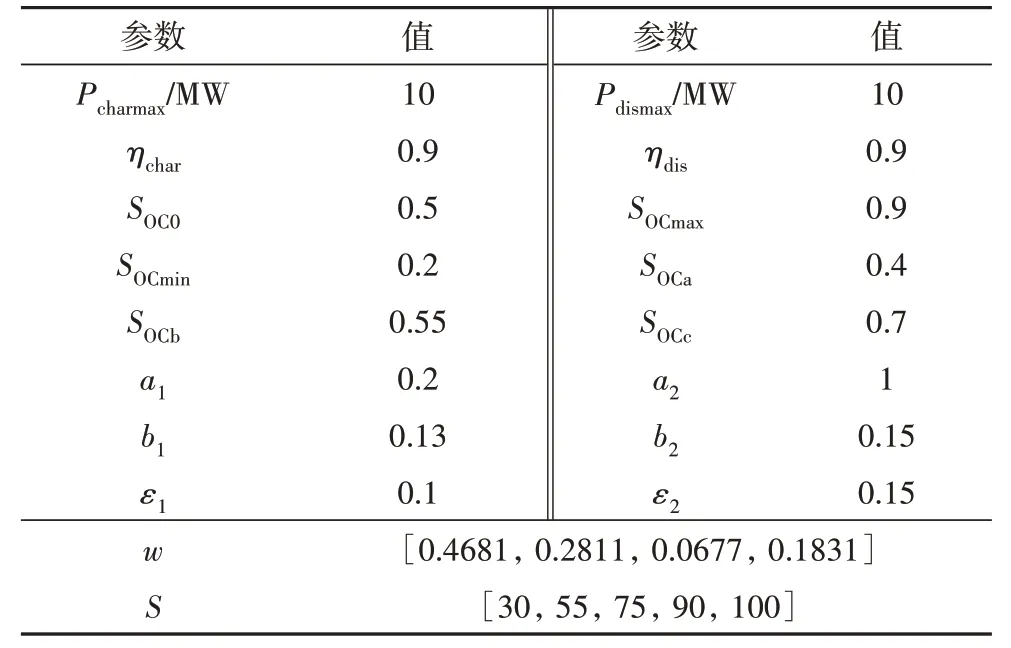
表1 控制参数表Tab.1 Control parameter table

为验证本文优化策略的有效性，设置3 个方案进行对比分析.方案一为无储能参与发电的情况；方案二为储能辅助风电跟踪计划发电，考虑储能充放电效率，并利用模糊控制优化电池SOC；方案三即本文提出的策略.优化结果如表2所示.

表2 各方案优化结果Tab.2 Optimization results of different schemes

各方案下的并网功率对比如图7 所示，并网功率准确率如图8 所示.可以看出，无储能情况下风电跟踪发电计划的准确率和合格率明显不高，部分点的准确率低于本文要求的90%，少量点甚至低于《风电场接入电力系统技术规定 第1 部分：陆上风电》（GB/T 19963.1—2021）要求的85%，总体的合格率仅为70.83%；方案二优化后，准确率明显提高，但储能过补偿使某些点准确率远高于合格要求，导致储能充放电容量被提前消耗，从而在准确率不足的点处无法提供足量补偿功率；本文策略，在准确率合格的时刻结合SOC 和波动率优化电池功率，而在准确率偏低的时刻进行功率补偿，整个优化周期内的合格率达到了100%，达到降低发电误差的控制目的.

图7 并网功率曲线Fig.7 Grid connected power curve

图8 并网功率准确率Fig.8 Grid connected power accuracy

图9为各方案下的并网功率波动图，按照表1参数ε2可知本文要求波动不大于总装机容量的15%，即7.5 MW.无储能时的功率波动最大为7.82 MW，大部分点的波动低于7.5 MW，波动合格率为99.31%.可以看出，风电功率本身已基本满足波动限制值，储能只需要对少数波动大的点进行平抑即可.方案二和方案三均使功率波动合格率达到100%.而方案二中2～4 h的波动远小于合格值，表明此时段储能过度平抑风电功率，造成电池充放电电量较大，从而使电池寿命损耗.方案三主要对18～20 h时段内波动较大的风电功率进行了平抑，而其他时段风储总功率的波动与原始风电功率波动差距不大，有效降低了电池出力.

图9 功率波动图Fig.9 Picture of power fluctuation

综合图10、图11和图12分析，可以发现：方案二的SOC变化幅度较大，变化范围在0.30～0.81，储能出力较大，单次DoD 超过了30%，动作次数67 次；而方案三的SOC 变化相对平缓，SOC 在0.41～0.70 之间波动，波幅较方案二降低了40%，储能最大出力相对小，单次DoD 保持在20%以下，动作次数61 次.由表2 可知，方案二的电池充电电量和放电电量分别为16.092 MW·h 和8.022 MW·h，而本文电池充电电量和放电电量分别为11.978 MW·h 和3.812 MW·h.以上数据表明，本文策略有效减少了优化时段内电池的充放电电量，降低了电池寿命损耗.

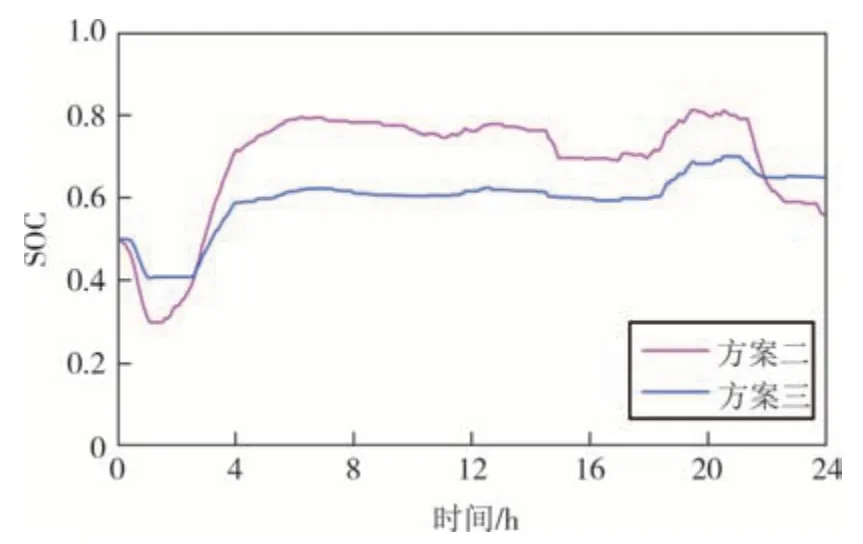
图10 储能系统SOC变化曲线Fig.10 SOC curve of energy storage system

图12 储能系统充放电深度Fig.12 DoD of energy storage system

5 结论

针对风力发电并网功率波动大、随机性高及风速预测不理想的问题，本文采用电池储能站对风电站进行功率补偿，为提高电池储能的补偿效率及延长电池循环实验寿命，提出了多目标优化控制策略，具体如下：

1）综合考虑跟踪发电计划曲线、平抑风功率波动及降低储能电池寿命损耗的需求，建立了多考核指标的评价体系，并进一步建立了储能站输出功率的多目标优化模型.

2）采用NSGA-Ⅱ智能算法求解多目标优化模型，并使用模糊综合评价进行最终决策，基于指标评价体系选取最优的储能站输出功率指令.

3）基于某风力发电场实际运行数据进行算例验证.相比文中对比方案，本方案SOC 波动幅度降低了40%，24 h 内储能动作次数降低6 次，延长了储能电池循环寿命，并在跟踪发电计划和平抑并网功率波动方面均具有一定的有效性及优越性.