基于傅里叶变换的双音多频信号识别实验设计

夏玉杰 崔建华 高 雅

(洛阳师范学院 物理与电子信息学院,洛阳 471934)

随着计算机技术的应用和信号处理技术的迅速发展,傅里叶变换已成为信号分析与系统设计不可缺少的重要工具[1]。傅里叶变换在信号处理课程群中处于核心作用,建立以时间为自变量的“信号”与以频率为自变量的“频谱”间的变换关系,是连接时域与频域的重要分析方法[2]。但是,傅里叶变换的数学分析多且公式复杂,学生学习中存在较多困惑和疑难问题[3-6],且运用傅里叶变换解决信号处理领域中复杂工程问题的能力普遍不足[7-9]。

为帮助学生理解并掌握傅里叶变换及其应用,本文首先梳理了傅里叶变换在自变量“时间”或“频率”取值连续或离散的四种形式,然后设计了基于傅里叶变换的双音多频(Dual Tone Multiple Frequency,DTMF)音频信号按键值识别综合实验。该实验以录制的电话拨号DTMF音频信号为对象,通过信号分段滤波、频谱分析、特征频率提取和判断识别等环节,带领学生学习利用傅里叶变换识别DTMF音频信号中的按键值;通过该实验的研究性拓展设计,培养学生对傅里叶变换的运用能力和创新探索能力。

1 傅里叶变换关系分析

在信号处理类课程教学中,信号在时域上分为连续时间信号和离散时间信号,频谱分为连续谱和离散谱。连续时间非周期信号和离散时间非周期信号的频谱分析分别为连续时间傅里叶变换(Continuous Time Fourier Transform,CTFT)和离散时间傅里叶变换(Discrete Time Fourier Transform,DTFT),连续时间周期信号和离散时间周期信号的频谱分析分别为傅里叶级数(Fourier Series,FS)和离散傅里叶级数(Discrete Fourier Series,DFS)。四种信号的频谱特征如表1所示。

表1 信号傅里叶变换形式表

抽样定理是联系连续时间信号和离散时间信号的桥梁,离散时间信号的DTFT频谱是连续的,而实际数字处理系统要求信号在时域和频域均是离散且有限长的。时域和频域均为有限长序列的频谱分析方法为离散傅里叶变换(Discrete Fourier Transform,DFT)。

在时域,以Ts为间隔对连续时间非周期信号x(n)进行时域抽样,形成离散时间非周期序列x(n),再加窗截断后得到N点有限长序列xN(n);在频域,连续时间非周期信号x(t)的频谱X(Ω)以Ωs=2π/Ts为周期延拓形成序列x(n)的连续周期频谱X(ejω),在[0,2π)内以2π/N为间隔对X(ejω)进行频域抽样,得到序列xN(n)的N点离散频谱xN(k),信号频谱分析的傅里叶变换关系如图1所示。

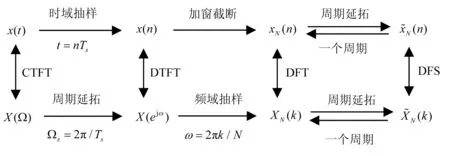
图1 信号频谱分析的傅里叶变换关系

2 DTMF信号识别实验设计

信号的频谱分析和特征频率提取是信号处理领域中的热点问题,傅里叶变换作为信号频谱分析的重要手段,在信号处理领域中应用广泛[8-11]。为帮助学生更好地理解傅里叶变换的应用,设计了基于傅里叶分析的DTMF音频信号按键值识别实验。

2.1 DTMF原理

DTMF信号是将两个特定的单音频信号进行组合来表示特定数字信号的编码方式,广泛应用于电话拨号和交互式控制系统[10-12]。DTMF信号由低频群和高频群两组不同频率组成,按键0～9和DTMF信号的频率组合对应关系如表2所示[13-14]。

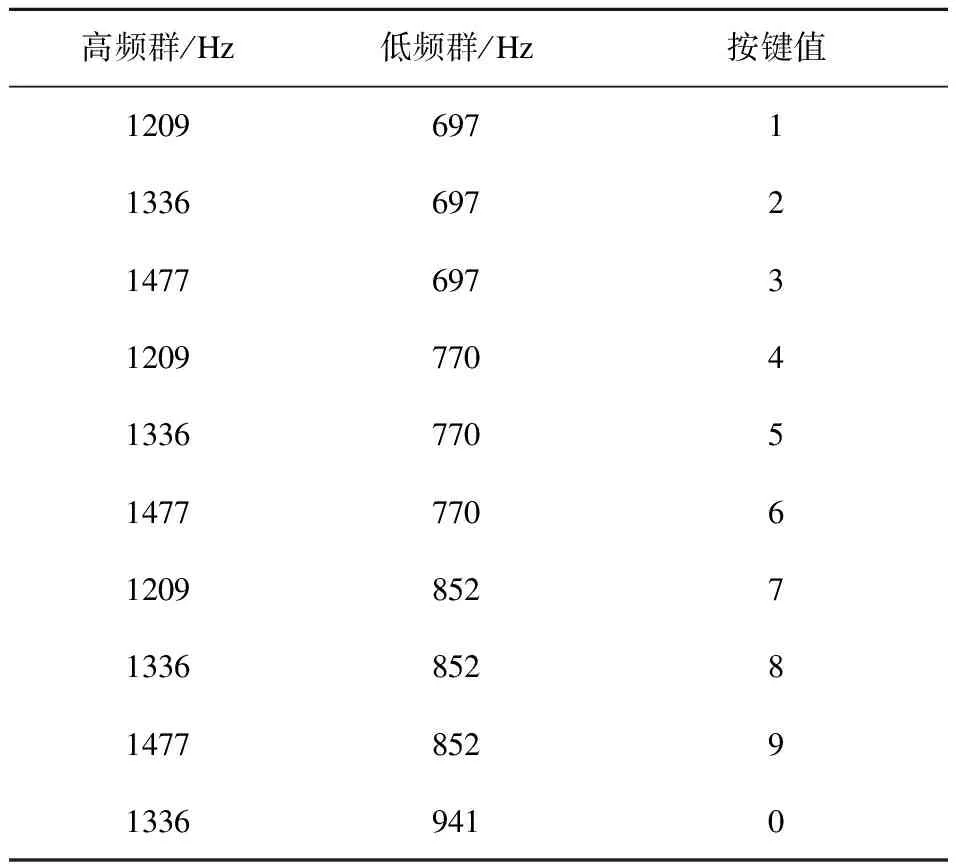
表2 DTMF信号频率与按键数字对应表

2.2 实验内容

利用电脑自带的录音机,录制一段手机键盘拨号的音频文件(M4A格式),例如“1326547890”。该音频信号的时间长度为6.5 s,采样率fs=44100 Hz。利用Matlab读取该音频文件数据,通过信号分段滤波和DFT频谱分析提取信号的特征频率,利用表2判断识别相应的按键值。

2.3 实验设计

DTMF信号的最高频率为1477 Hz,录制拨号音频信号的采样率fs=44100 Hz,满足抽样定理。音频信号是离散时间非周期序列,由DTFT分析可知其频谱是连续的。为了便于数字系统处理,在时域对音频信号加矩形窗进行分段处理,分段长度为N=4096点,由DFT分析知其频谱离散。

由于每个按键信号是由两个特定的单音频信号叠加组合,因此对分段的拨号音频信号利用DFT的快速傅里叶变换算法(Fast Fourier Transform,FFT)提取其特征频率,在合理的误差范围内对照表2即可正确识别对应的按键值。DTMF信号识别实验的设计流程如图2所示。

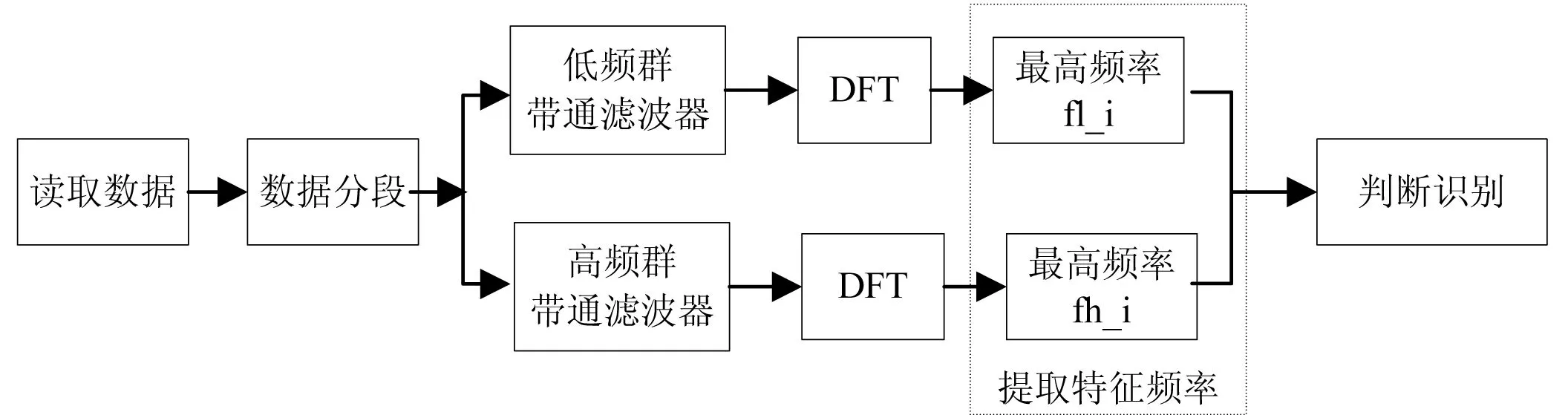
图2 DTMF信号识别实验设计流程

(1)读取录制的拨号音频数据:调用[x_sig,fs]=audioread(filename)函数读取音频数据,返回值x_sig为filename文件数据,fs为采样率44100Hz。

(2)分割有效的拨号信号段:利用[x_i,fs]=audioread(filename,samples)函数对音频中10个DTMF拨号信号分段,其中samples是filename文件的数据范围,各信号段均取N=4096个采样点。

(3)设计通带为697～941 Hz的低频群带通滤波器和1209～1477 Hz的高频群带通滤波器:利用bandpass(Fstop1,Fpass1,Fpass2,Fstop2,Astop1,Apass,Astop2)函数设计带通滤波器,其中Fstop1和Fstop2为阻带左右边界频率,Fpass1和Fpass2为通带左右边界频率,Apass为通带最大衰减,Astop1和Astop2为左右两侧过渡带最小衰减。

低频群带通滤波器BPF_low参数选取:Fstop1=500 Hz,Fpass1=697 Hz,Fpass2=941 Hz,Fstop2=1000 Hz,Astop1=30 dB,Apass=1 dB,Astop2=30 dB。

高频群带通滤波器BPF_high参数选取:Fstop1=1000 Hz,Fpass1=1209 Hz,Fpass2=1477 Hz,Fstop2=1600 Hz,Astop1=30 dB,Apass=1 dB,Astop2=30 dB。

(4)对第i段分段数据段分别通过低频群带通滤波器x_low_i=filter(BPF_low,x_i)和高频群带通滤波器x_high_i=filter(BPF_high,x_i)滤波。

(5)分析第i段数据滤波后信号频谱:利用DFT的快速傅里叶变换算法FFT(x_low_i)和FFT(x_high_i)提取信号特征频率,获得第i段数据的低频群最高频率fl_i和高频群最高频率fh_i。

(6)通过DTMF频率表和特征频率(fl_i,fh_i)在设定频率误差门限内比较,判断识别对应键值。

2.4 实验结果与分析

录制的音频信号时域和频域波形分别如图3(a)和图3(b)所示。图3(a)可见,由于不同按键值拨号的持续时间不同,各按键对应信号段的时域波形也不同。图3(b)表明,音频信号频率集中在约650～950 Hz和1200～1500 Hz,这与DTMF信号发送频率基本一致。由于存在背景噪声,其他频率上也存在较小的频率分量。

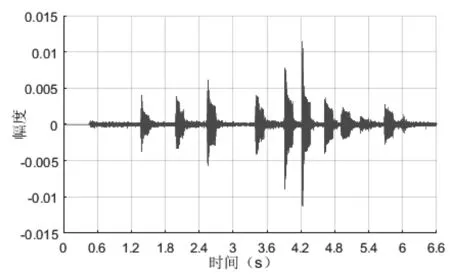
(a) 音频信号的时域波形

低频群和高频群带通滤波器输出的分段信号时域波形(以第1个信号段为例)如图4所示。其中,图4(a)为第1个信号段滤波前的时域波形,图4(b)为第1个信号段通过低频群带通滤波器的输出时域波形,图4(c)为第1个信号段通过高频群带通滤波器的输出时域波形。可以看出,低频群带通滤波器和高频群带通滤波器输出的信号频率不同。这是由于低频群和高频群带通滤波器的通带频率不一致,这两个带通滤波器的目的是保证对应频带信号顺利通过,从而消除其它频率干扰。

(a) 第1个信号段滤波前时域波形

分段信号的特征频率提取和按键值识别结果如图5所示。可以看到,基于DFT的快速傅里叶变换能够有效提取各段信号的特征频率,并可正确识别出按键值“1326547890”。以第1段信号段的DFT分析为例,低频群带通滤波器的输出信号最高频率fl_i=699 Hz,高频群带通滤波器的输出信号最高频率fh_i=1205 Hz,则第1段信号的特征频率为(699 Hz,1205 Hz)。DFT频率分辨率为10.8 Hz,提取的特征频率(699 Hz,1205 Hz)和数值“1”的DTMF频率(697 Hz,1209 Hz)存在较小误差。设定频率误差门限为22 Hz,则第1个信号段的按键值识别结果为“1”。

图5 分段信号的特征频率提取和按键值识别结果

3 研究性实验拓展

为了培养学生的研究思维和创新能力,本实验设计还可从以下几个方面进行开放性拓展研究:

(1)探讨分段信号长度N对特征频率提取精度的影响;

(2)分析低频群和高频群带通滤波器参数选取对信号滤波的影响;

(3)分析提取的特征频率与实际DTMF频率不完全一致的原因;

(4)探讨特征频率提取的误差门限设定对按键值识别的影响。

上述开放研究性实验拓展不仅能够提高学生对傅里叶分析基本原理的认知,加深学生对抽象理论的理解,而且能够激发学生的科研活动兴趣,驱动创新思维发展,提升学生解决复杂工程问题的多维分析能力和实践创新素质,形成傅里叶分析在信号处理中知识、能力、素养的有机融合。

4 结语

针对傅里叶变换的学习难点梳理和分析了傅里叶变换四种形式和关系,重点设计了DTMF电话拨号音频信号的按键值识别综合应用实验。该实验将音频信号的DFT频谱分析和特征频率提取引入教学,利用Matlab仿真工具进行程序设计和功能验证,有助于加强学生对傅里叶变换原理和工程应用的理解,培养学生利用信号处理的基本理论解决复杂工程问题的科学素养和实践技能。