稳健的稀疏信号单快拍波达方向估计

虞 飞，宋 俊，余 赟，苏 冰

(海军研究院，北京 100071)

0 引 言

基于稀疏重构理论的阵列测向方法是近十年阵列信号处理领域新发展起来的十分活跃的一个研究分支，已取得了丰硕的理论成果[1-4]。这类方法在传统的基于子空间的超分辨算法的基础上，引入了目标信号的空间稀疏信息，从而大大提高了目标信号的到达角估计性能。传统的子空间类到达角估计算法要求在高信噪比、非相关、大样本、理想阵列流形条件下才可获得优异的性能[5-7]，尽管近年来围绕其中某一种非理想因素进行算法优化的研究成果很多[8-10]，但是算法的实用性因实际使用场景下多个非理想因素往往同时存在而大大受限。

稀疏重构类到达角估计方法之所以能够成为近年来的研究热点，关键原因在于此类方法在低信噪比、相干背景、小样本、阵列未校准等不利条件下都具有良好的目标信号测向精度和多目标分辨能力，相对于传统的子空间类算法在实用性方面具有更大潜力[11]。

虽然稀疏重构类到达角估计方法在整体鲁棒性方面优于子空间类估计技术，但是前者的主流算法在计算复杂度方面处于相对劣势，而且还涉及额外的正则化参数选取问题。本文通过稀疏重构得到传感器阵列输出数据的稀疏表示模型，提出了一种基于最小均方误差(Minimum Mean-Square Error,MMSE)准则迭代实现的单快拍到达角估计算法(Iterative Implementation of MMSE, II-MMSE)。该算法采用MMSE框架，考虑了阵列接收数据中的模型“噪声”协方差信息，对于阵列模型误差具有较好的鲁棒性。II-MMSE算法保持了稀疏重构类到达角估计方法在诸多非理想因素下的整体鲁棒性优势，克服了主流稀疏重构类方法的高计算复杂度问题，而且避免了正则化参数选取，进一步推动了稀疏重构类到达角估计方法的工程实用化。

1 阵列输出模型的稀疏重构

考虑K个远场窄带平面波入射到由M个无指向性单元构成的传感器阵列，且K个信号与传感器阵列位于同一平面内。将目标信号可能到达角范围空间Θ进行N次均匀网格划分，可将传统的阵列输出模型转化为稀疏重构模型[11]：

2 基于MMSE准则迭代实现的单快拍DOA估计算法

根据最小均方误差(MMSE)准则和式(1)中的稀疏重构模型，取目标函数f(t)：

式中：W(t)为M×N维复权矩阵，γ(t)显然是经过M×N型滤波器组滤波后的期望输出信号矢量。根据Wiener滤波器理论相关结论，容易求得式(2)中的目标函数在MMSE意义上的最优权矩阵为

假定γ(t)与n(t)之间相互统计独立，则由式(1)可得：

式中：Rn=E[n(t)nH(t)]为M×M维噪声协方差矩阵，对于功率为σ2n的空间高斯白噪声，Rn可以简化为Rn=σ2nIM，P=E[γ(t)γH(t)]为N×N维稀疏信号协方差矩阵。假设稀疏信号矢量γ(t)内各个分量互不相关，则有：

其中：pn=E[γn(t)γ*n(t)]，n=1，…，N，故P可称为稀疏功率对角阵。

由式(4)和(5)，可将式(3)进一步表示为

采用空间匹配滤波器(Matched Filter, MF)即常规波束形成(Conventional Beamforming, CBF)算法，可以得到稀疏信号γ(t)的粗略估计：

(t)可作为MMSE迭代算法中稀疏信号γ(t)的初始估计值：

则稀疏功率对角阵的初始值为

式中：⊙表示矩阵的哈达玛(Hadamard)乘积，即矩阵对应元素乘积。再由式(7)可得MMSE迭代算法中权矩阵的更新值：

式中：下标i表示第i次迭代。稀疏信号γ(t)的最小均方误差估计值为

类似于式(10)，可得第i次迭代时稀疏功率对角阵的估计为

式(11)、(12)和(13)构成了MMSE迭代算法第i次迭代的实现过程。当某一次迭代估计值满足ε为某一预先指定的较小正数时，算法停止迭代，或者当算法达到预设的最大迭代次数时也停止迭代。此时，由稀疏功率对角阵的估值构成的列向量diag[(t)]关于到达角网格的稀疏功率谱中，第K个谱峰对应的角度即为目标信号到达角估计值

综合以上分析，现将MMSE迭代算法的完整流程归纳如下：

(1) 初始化

对于t时刻的阵列接收数据x(t)，有

(2) 迭代过程

(3) 算法结果

在列向量diag[(t)]关于到达角网格的稀疏功率谱中，第k个谱峰对应的角度值即为目标信号到达角估计值

3 算法收敛性分析

下面分析MMSE迭代算法的收敛性。为了说明MMSE算法迭代的收敛性，首先建立稀疏信号矢量估计的递推表达式。由式(11)、(12)和(13)可得：

式中：“(·)†”表示矩阵的穆尔-彭罗斯(Moore-Penrose)逆。在实际应用中，噪声协方差矩阵Rn不能忽略。迭代过程式(15)实际上是如下加权最小范数优化问题的一种递推形式[12]：

式中：W为N×N维权矩阵，且W为对角阵，其迭代形式为Wi=diag[(t)]。在每一步迭代中，目标函数都有如下关系：

其中：wk为权矩阵W的第k个对角元素，γk(t)为稀疏信号矢量γ(t)的第k个元素。

由式(17)可以看出，权矩阵W中某个对角元素相对越大，γ(t)中的相应位置元素对目标函数最小化的贡献就相对越小，即惩罚值越小。反之亦然。因此，如果稀疏基矩阵Φ中的某一列相对于其他列来说能更好地匹配阵列测量数据x(t)，那么γi-1(t)中的对应位置元素迭代到下一步时将得到更大值。这样，通过设定一个可行的初始化稀疏信号矢量估计，如可使目标函数(17)在最小化的迭代过程中，逐渐强化γ(t)中某一个大小相对突出的元素，同时逐渐抑制剩余元素的大小，直至γ(t)达到预设的估计精度或者这些受抑制元素近似全为0，此时算法收敛，停止迭代。这时，仅选取稀疏基矩阵Φ中的某一列来最佳地匹配阵列测量数据x(t)。

由式(17)容易得出第i次迭代时的目标函数为

综上分析可知，式(18)中的递推问题收敛到最稀疏解意味着当i→+∞且(t)≠0时，有而MMSE迭代算法的收敛条件可以进一步写成：

因此，如果当i→+∞且(t)≠0时，有成立，则也成立，从而说明MMSE迭代算法是收敛的。

应注意，MMSE迭代算法并非在任意初始化条件下的收敛都是有意义的，例如当(t)=0时，γ(t)每步迭代的结果都为0。因此，不失一般性，可假定初始化稀疏信号矢量(t)的非0元素个数始终为N。另外，权矩阵W的对角元素wk=0意味着，通过运算ΦWi使稀疏基矩阵Φ中的相应列变成了0向量，说明相应的子空间被排除出了信号子空间。

4 阵列模型误差下的算法性能分析

在实际应用中，由于传感器基阵工作环境中的介质扰动、阵列长期未校准或存在校准误差、阵列有限采样引起的幅相量化误差等，都可能导致传感器基阵模型产生误差。结合式(1)，含有阵列模型误差的阵列输出响应一般可以定义为

式中：z为M×1维未知的阵列模型误差矢量，其第m个元素可表示为

其中：Δam和Δφm分别为阵元m上的随机幅度误差和随机相位误差。假设各阵元具有独立且同分布的零均值随机幅值误差和随机相位误差，则各阵元之间的模型误差是互不相关的，但具有相同的模型误差的方差σ2z。式(20)还可以表示为

式中：nz(t)=[Φγ(t)]⊙(z-IM×1)等效为阵列模型误差引起的“噪声”矢量，这里IM×1为M×1维全1向量。由模型误差的假设可知nz(t)为M×1维零均值矢量。

类似于式(11)，可得存在阵列模型误差时，MMSE迭代算法的权矩阵更新为

式中：Rnz=E[nz(t)nHz(t)]表示模型噪声协方差矩阵，且有：

其中：Z=diag[z1，…，zM]-IM。在式(24)的推导过程中，还利用到了Hadamard乘积的运算性质A⊙B=B⊙A和(A⊙B)H=AH⊙BH[13]。根据式(24)的结果，则权矩阵的更新变为

在式(25)中，Rn为仅依赖于噪声的固定协方差矩阵，而σ2zIM⊙[H]是依赖于信号功率更新估计的自适应噪声协方差矩阵。当有高功率信号源存在时，可能导致算法对噪声功率的低估，或者存在阵列模型误差等情形时，都可能会引起小的伪峰，而模型噪声协方差项σ2zIM⊙[H]的存在为信号源的功率估计建立了一个可接受的动态范围，恰好消除了这些伪峰的影响，从而使本文算法具有自适应能力，表明MMSE迭代算法对阵列模型误差具有较好的鲁棒性。

为了增强算法的自适应能力，可对式(25)进行以下修正[14]：

其中，通过引入尺度因子α(0＜α＜1)降低了噪声协方差项Rn，可以进一步增强算法的自适应能力，使自适应噪声协方差项在权矩阵更新过程中的相对贡献更大。

5 仿真实验

考虑两个等功率的相干窄带远场平面波分别从不同方向入射到由12个传感器阵元按照半波长间距布阵构成的均匀线列阵，阵列对空间信号进行单快拍采样。定义信噪比RSN=10lg(Psσ2n)，如无特殊说明，实验中取RSN=10 dB。

实验中，第l个阵元对应的模型误差可表示为

式中：ρ为相对于标准差的百分比，N(0，1)为零均值，单位方差的实高斯随机分布噪声。由式(21)可知，E[zl]=1，则故可以通过zl-1的1 000次独立实现来估计zl的方差，即。显然，ρ越大，模型误差的方差也越大，而ρ=0、α=1时，算法退化为理想阵列模型。如无明确说明，实验中噪声协方差尺度因子α=1/8。

5.1 算法收敛性实验

假设两个目标信号分别以到达角参数θ1=-10°，θ2=60°入射到上述传感器阵列，阵列模型误差百分比ρ=10。图1为II-MMSE算法分别在初始化、迭代1次、5次和10次过程中对目标信号到达角的归一化稀疏功率谱图。这里算法初始化结果为通过空间匹配滤波器估计所得。

图1 II-MMSE算法迭代不同次数得到的两个信号到达角估计的归一化功率谱Fig.1 Normalized power spectrums of the DOA estimate for two signals obtained by the II-MMSE algorithm with different times of iterations

从仿真结果可发现，尽管存在阵列模型误差，II-MMSE算法仍能在真实目标方向角上形成尖锐谱峰，表明算法对目标信号具有良好的到达角估计精度和多目标分辨能力。当算法迭代到一定次数时(一般不超过15次)，功率谱图的伪峰及旁瓣逐渐被抑制，且目标方向对应的谱峰十分尖锐，表明算法达到收敛状态。

5.2 算法对多目标信号的角度分辨率

假设两个空间方位邻近信号分别以到达角参数θ1=-10°、θ2=-5°入射到上述传感器阵列，阵列模型误差百分比ρ=10%。图2给出了采用II-MMSE算法、L1-min算法[15]和常规波束形成(CBF)算法对目标信号到达角估计的归一化稀疏功率谱图。

图2 三种不同算法得到的两个邻近信号到达角估计的归一化功率谱Fig.2 Normalized power spectrums of the DOA estimate for two adjacent signals obtained by three different algorithms

由图2中的仿真结果可看出，对于空间上方位邻近的两个目标信号，采用II-MMSE算法和L1-min算法均具备对目标信号的高方位分辨能力，而常规波束形成算法不具备这一能力。另外发现，L1-min算法的稀疏功率谱具有较多的小幅度伪峰，而II-MMSE算法几乎没有伪峰和旁瓣影响。实验中还发现，当阵列模型误差百分比ρ=0时，L1-min算法的伪峰也几乎被抑制。上述结果表明，IIMMSE算法对阵列模型误差具有一定的鲁棒性，而L1-min算法不具备这一特性。

5.3 信噪比对到达角估计精度的影响

考虑两个目标信号分别以到达角参数θ1=-10°、θ2=60°入射到上述传感器基阵，阵列模型误差百分比ρ=10。对前述3种算法分别进行300次蒙特卡洛(Monte Carlo)仿真实验，得到如图3所示的目标信号到达角估计的均方根误差(Root Mean Square Error, RMSE)随信噪比的变化关系。

图3 三种算法到达角估计的RMSE随信噪比的变化曲线Fig.3 Variation curves of the RMSE of DOA estimation with SNR by the three algorithms

从图3中的仿真结果可发现，在阵列模型存在误差的情况下，II-MMSE算法对目标信号到达角的统计估计精度明显高于另两种算法。在低信噪比时这一优势更加明显。

5.4 计算复杂度分析和计算时间比较

由式(26)可知，本文提出的II-MMSE算法的计算复杂度为O(N2M)。而L1-min算法通过文献[11]中的分析可知，其计算复杂度为O(N3)。另外，由式(8)可知，CBF算法的计算复杂度为O(NM)。考虑到在实际应用场景中，N≫M，因此在这3种估计算法中，L1-min算法的计算复杂度最高，其次是II-MMSE算法，CBF算法的计算复杂度最低。

表1中列出了上述3种估计算法在不同信噪比下的平均计算时间。实验中，取两个相干信号分别以DOA参数θ1=-10°、θ2=60°入射到上述均匀线阵，阵列模型误差百分比ρ=10%，Monte Carlo仿真实验次数为50。仿真环境：采用Matlab R2009a平台，Intel Core 2处理器，2G内存。通过比较这3种算法的计算时间可以看出，II-MMSE算法的计算效率远高于L1-min算法，但这两种算法的计算效率都明显低于CBF算法。但II-MMSE算法和L1-min算法在整体性能上优于CBF算法。

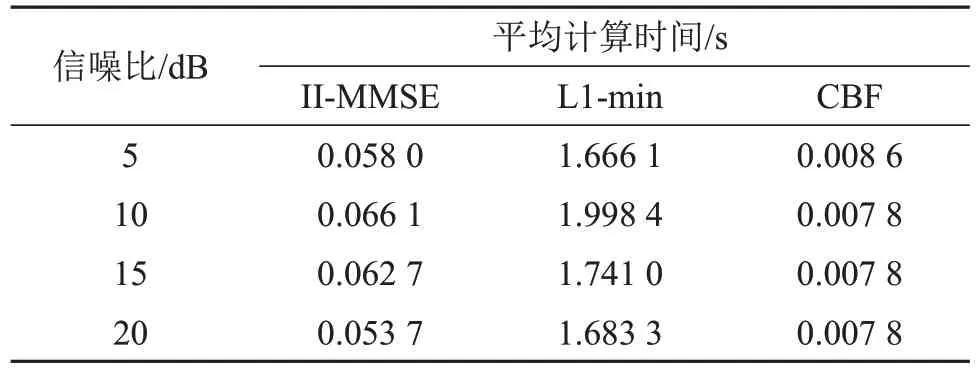
表1 不同信噪比下三种算法的平均计算时间Table 1 Average computation times of the three algorithms under different SNRs

6 结 论

本文通过稀疏重构得到传感器阵列输出数据的稀疏表示模型，提出了一种II-MMSE算法，理论分析了II-MMSE算法的迭代收敛性和对阵列模型误差的鲁棒性，评估了该算法的计算复杂度。理论分析和仿真结果都表明II-MMSE算法保持了稀疏重构类到达角估计方法在低信噪比、相干背景、小样本、阵列未校准等诸多非理想因素下的整体鲁棒性优势，而且计算效率更高，无需选取正则化参数，具有潜在的工程推广价值。