基于优化匹配追踪稀疏分解的微弱超声回波提取

苏映新

(辽东学院信息工程学院，辽宁丹东 118000)

0 引 言

超声具有指向性好、声能集中和穿透力强的特点，因其精度高、便于携带而在超声无损缺陷检测[1]、农业病虫超声雾化防治[2]，机械零件应力消除[3]等工农业、航空和军事领域具有广泛的应用。然而受环境噪声影响，超声回波信号的幅度通常较小且包含大量噪声，因此提高低信噪比超声回波提取性能是不可或缺的技术手段[3]。

Sinding等[4]对超声回波信号进行了正则化处理，显著提高了算法的处理速度和信噪比，相比于传统带通滤波具有较好的回波参数估计性能。Abbass等[5]根据随机选择移位算法改进小波阈值算法，该算法的平移不变性提高了小波变换的降噪效果，但当回波信号存在强噪声时容易造成失真。王大为等[6]根据超声回波的频率结构与噪声频率结构不同的特点，设计双高斯衰减模型进行参数最优估计，以重构超声信号。章涛等[7]由回波波峰实时更新阈值，通过一致性判断和自动补偿，获取回波的精确特征点。

上述方法通常难以满足低信噪比回波信号的降噪和检测要求[8]。匹配追踪(Matching Pursuit, MP)算法能够根据信号稀疏性进行分解并重构，无需先验信息，适于各种非平稳和强噪声环境下的声音识别。陈秋菊等[9]将改进的MP稀疏分解用于强噪声环境下异常声信号识别，通过信号重构对低信噪比信号进行降噪增强；Cho等[10]结合MP稀疏分解和短时谱估计对低信噪比声信号进行分解和二次重构，提高信号的检测和识别精度；Jorge等[11]采用MP稀疏分解提高声音信号的信噪比。

根据已有研究，借鉴匹配追踪在低信噪比语音信号检测方面的成果，本文提出自适应MP稀疏分解的超声回波检测算法。算法通过构建合适的目标函数和重构函数，由自适应粒子群优化(Particle Swarm Optimization, PSO)算法对MP稀疏分解进行优化，通过连续Gabor原子集提高了MP进化过程中最优原子的匹配度，最后通过回波信号重构实现对回波的降噪和提取，实验验证了算法的有效性和鲁棒性。

1 匹配追踪信号稀疏分解

设集合D={gi}，i=1，2，…，Q。D中元素gi为张成空间H=RN所需的单位矢量，且有Q≫N，Q为集合D的规模，N为空间H的维数，则D为构成空间的超完备库。对于任意信号f∈H都可以由D中若干原子的线性组合表示[11]，即f=a·g，a={α1，a2，…，am}为展开系数，g={g1，g2，…，gm}为稀疏分解原子集。从D库中选取g1i，使其满足[9]：

式中：gi1为最优匹配原子，表示内积，max(·)为取最大值函数，此时，回波信号f可分解为f=R1f为剩余信号，对R1f重复分解且令R0f=f，则f可表示为

实验表明，随着次数k增加，Rkf逐渐趋向于0[14]，此时信号f可实现稀疏分解。

实际超声回波检测时MP稀疏分解对字典遍历的有限性要求与其超完备集需求存在矛盾。PSO算法具有较好的连续空间搜索特性[11]，因而如果通过目标函数和重构函数的合理改进，将PSO的连续空间搜索能力融入MP稀疏分解中，可以避免参数离散化对字典冗余度的影响。

2 自适应MP稀疏分解

2.1 PSO算法参数自适应改进

PSO算法[12]具有较好的连续空间搜索能力，其描述了种群粒子以一定的速度在d维空间飞行，并根据个体和种群的历史最优位置更新粒子当前的位置。但当算法的最优粒子不是全局最优且无更优解时，算法陷入局部最优，或在收敛速度和稳定上产生矛盾[7]。为此，需对算法的惯性因子和学习因子进行自适应调整。

惯性权重w值影响算法的全局和局部搜索性能，为此，采用具有非线性动态惯性特性的权重系数，以平衡其全局和局部搜索性能，其表达式为[11]

式中：favg和fmin分别为粒子的平均和最小适应度值，f为当前粒子的适应度值，wmax和wmin为当前惯性权重的边界极值。由式(3)可知当f≤favg时，粒子的w较小，受到保护；而当f＞favg时，粒子的w=wmax，算法驱动粒子向最优区域搜索靠拢，从而提高算法的搜索能力。

粒子搜索时应设置合理的最优速度，第i次迭代中粒子可搜索的速度界为

式中：和为搜索边界，npop为群粒子数，当粒子的搜索速度超过时，其速度需以原有方向随机更新，可见限定了粒子可以达到的最远距离。

为了解决PSO算法因收敛过快而陷于局部最优解问题，在迭代过程中，增加最优粒子的扰动有利于粒子从局部最优中解放出来[9]。与高斯型Gabor原子集相适应，采用高斯概率密度函数变异扰动Gi(t)，即：

2.2 自适应粒子变异

设粒子群算法在迭代优化过程中，粒子间的距离值s(L)可表示为

式中：Laj为粒子j与当前划分簇中最优粒子之间的欧氏距离。如果当前最优粒子gbest在相邻k次迭代内无明显改善，则需对其进行自适应变异，其表达式为

式中：为根据式(6)计算的粒子间距，Lmax和Lmin分别为其极大、极小值。

自适应交叉因子根据粒子个体适应度值的大小进行动态调整，其计算公式为

式中：CRL和CRL为交叉因子上下限，学习因子影响PSO算法的粒子间继承性，文中学习因子的自适应设置方式为

式中：c0为调整所需比例因子，与为第k次迭代过程中粒子i的个体历史最优位置和种群的历史最优位置。

在粒子群更新过程中，如果给定随机数r∈[0，1]满足r≤p，则对当前粒子进行变异操作，其变异操作过程为

式中：、和分别为粒子位置矢量。

超完备集中原子特性与超声回波特性相匹配是完成信号稀疏分解的关键，由高斯窗函数得到的Gabor字典集，其原子特性与超声回波特性具有较好的相似性[10]。由于D是连续的，其包含的原子数将远超过传统参数离散化Gabor集，因而其最优匹配原子可以更准确地反映原信号的结构特性。同时文中算法可实时计算最优原子，减少原子集遍历的时间开销。

2.3 PSO优化稀疏分解目标函数构建

设超声回波模型为f=fs+fn，式中fs为纯净回波信号，fn为叠加的噪声信号，则文中文中自适应MP稀疏分解的目标函数为

式中：J(·)表示内积。重构回波信号的方法为

式中：gbest={gi|maxJ(f，gi)，gi∈D}，为根据式(12)所示目标函数通过自适应MP稀疏分解得到与信号最优匹配的原子，其参数γbest={s，u，v，ω}反映了回波特征。文中自适应MP稀疏分解超声回波提取流程图如图1所示。图1中Pb(i)和Pglobal分别表示粒子的个体最优位置和种群全局最优位置。

图1 超声回波信号提取流程图Fig.1 Flow chart of ultrasonic echo signal extraction

3 实验分析

为验证所提回波提取算法的有效性，实验选用RAM-5000超声无损检测系统，以金属构件拉伸疲劳为检测对象，以无激励在安静实验室检测的噪声放大后作为实验用叠加噪声，采用均方误差(Mean Square Error, MSE)、波形相似性(Normalized Correlation Coefficient, NCC)[10]及信噪比(Signal to Noise Ratio, SNR)三个指标对重构回波信号进行性能评估，文中自适应MP稀疏分解算法(记为APSO-MP)中相关参数的设置如表1所示，表中N为信号长度，rand(·)表示生成(0, 1)内均匀分布随机数。

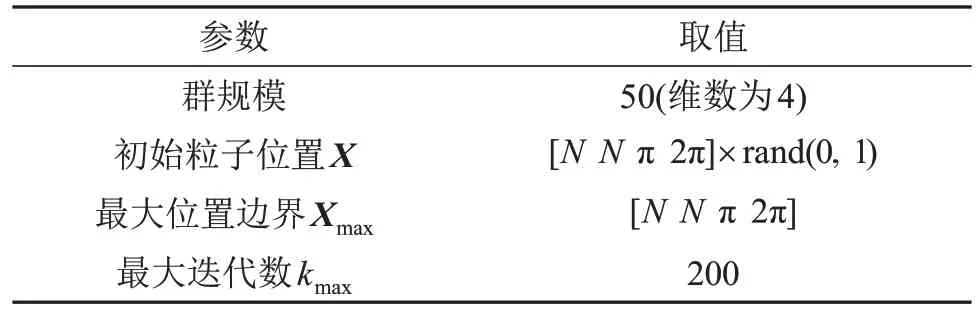
表1 自适应MP稀疏分解参数设置Table 1 Parameter setting of the proposed algorithm

如图2所示为一组无噪声及叠加噪声的回波信号，参数为带宽50 µs，中心频率f0=1 MHz，时延为20 µs，初相u0=0，采样率及点数fs=10 MHz、N为512，高斯白噪声方差σ=0.3，SNR为-4 dB。实验中通过调整带宽、中心频率、时延及初相等参数获得多组不同参数的超声回波信号，然后与噪声按不同的分段信噪比进行混合作为测试数据，以无噪声回波信号作为原始信号，将不同算法检测的回波信号与原始信号进行比较，并计算相应的评价指标以测试算法的回波检测性能。

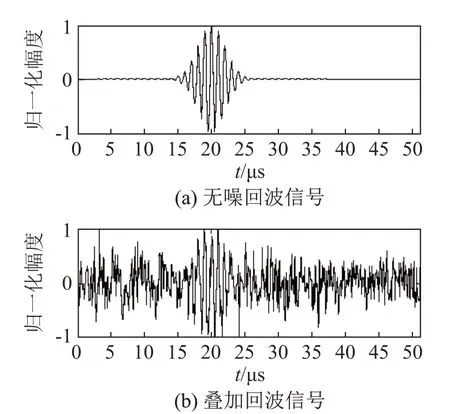
图2 有无噪声叠加的超声回波信号Fig.2 Ultrasonic echo signal with or without noise superposition

3.1 自适应MP稀疏分解性能分析

以原始正交MP算法(记为OMP)及经典PSO优化的MP算法(记为PSO-MP)[11]作为对比算法，与文中APSO-MP算法一起对测试数据进行稀疏分解和重构。分析三种算法的计算量和评估重构性能。实验结果如表2所示，表中结果为多次实验结果的平均值。

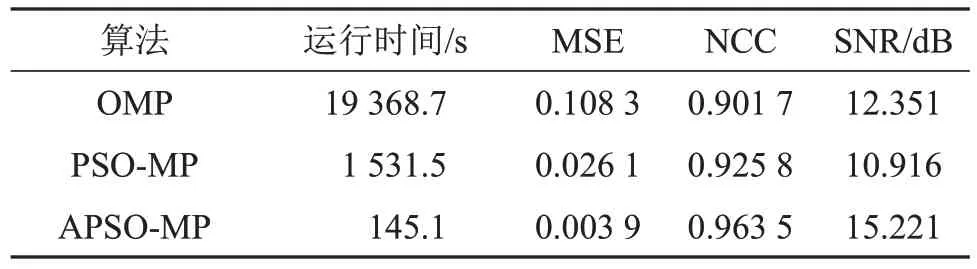
表2 三种比较算法实验结果平均值Table 2 Average experimental results of three algorithms

由表2结果可知，加入PSO算法，有效减少了稀疏分解的计算量，说明采用PSO对MP算法进行优化是有效的，并且APSO-MP算法进一步降低了计算量。从重构指标可以看出，PSO-MP算法的重构性能最差，主要因为其PSO相关参数的设置不能保证其与不同参数的回波信号之间的相关性，而文中算法的性能最优，主要是因为采用连续原子集，在每次迭代时，可以选择最佳匹配的原子，而不会因为原子参数离散化带来的精度损失，同时PSO参数自适应设置，可更好地适应不同参数超声信号。

3.2 算法性能比较实验

以SNR为-10 dB的含噪声回波作为测试数据，以小波阈值降噪法、EMD与S变换组合检测法(EMD+S)作为比较算法，实验结果如图3所示。从图3中的实验结果看出，APSO-MP算法可以较为准确地重构出原始回波信号，重构信号与原始回波信号具有相近的渡越时间，而小波阈值法与EMD+S算法的重构信号含有较多的噪声，且原始信号出现部分失真，回波的渡越时间不明晰。实验结果进一步验证文中APSO-MP算法在低信噪比下对超声回波信号降噪重构的有效性。

图3 不同算法的回波降噪重构实验结果Fig.3 Experimental results of echo-noise reduction and reconstruction for different algorithms

4 结 论

为实现低信噪比微弱超声回波信号的准确提取，本文提出了基于优化匹配追踪的稀疏分解回波提取算法。该算法首先优化了PSO参数，实现参数自适应设置，然后改进MP稀疏分解的目标函数和重构函数，实现自适应PSO优化的MP稀疏分解算法，并建立了连续超完备Gabor原子集，提高了最优原子与超声回波信号的匹配程度，最后重构回波实现对回波的降噪和准确提取。实验结果表明，本文所提识别算法显著降低了计算量，能够准确提取信噪比在-10 dB以上的回波信号，实验平均均方误差为0.004 7，平均波形相似系数为0.975 0，效果优于已有小波阈值等算法，且具有较好的识别鲁棒性。