煤炭港口设备维护调度优化研究

刘华琳 王 潇 李军伟

(国能黄骅港务有限责任公司1) 沧州 061113) (武汉理工大学交通与物流工程学院2) 武汉 430063)

0 引 言

Boland等[1-2]在研究澳大利亚猎人谷煤炭供应链年度维护问题时发现,将规划期内所有设备的维护检修任务作为一个整体考虑,协调起来制定检修计划,才能保证系统的总中断时间最短,从而达到在计划时间段内最大化系统通货能力的效果.该问题被抽象为一个带边中断动态网络最大流(MAXTFAO)问题,并被证明是强NP难的.同时还提出了多种基于智能搜索的优化算法有效解决了该问题,成功替代了以往需要20多人两个月完成的工作,并应用到了纽卡斯尔港NCIG码头的日常运营管理中,取得了显著的经济效益.

带边中断的动态网络最大流问题自然地混合了网络流和调度问题的特征.系统组件维护期间是不可用的,相应的抽象网络中对应的弧容量为0.每个维护任务的维护时间窗是相对固定的,其取决于设施设备的运行状态.这意味着弧容量是随着时间的推移而变化,即不同时间段内流量的相互依赖性和流量网络是动态的,这是典型的时间依赖动态容量网络问题.此外,网络中的弧是否中断取决于何时执行维护任务,这意味着网络在一定时间范围包含的时间段内的性能将在很大程度上取决于之前的时间段所做的决策,是调度的结果.

Pearce等[3]针对该问题特征设计了基于Branch and Benders cut(B&BC)的精确算法并提出三种有效的改进措施对该问题进行求解.相较于商业求解器,该算法均有不错的改进和表现.与Pearce算法不同,刘茜等[4]采用传统的Benders分解算法对该问题进行了算法实验.高吉冰等[5]将两位学者的算法进行了求解性能对比,其结果表明B&BC算法的性能更加优越,并基于该算法框架提出了多种有效的改进措施.徐齐鹏[6]设计了以禁忌搜索算法为主体,结合整数规划的混合算法,实验结果表明该算法在大网络大规模的算例中表现最好.

上述研究中均是假设网络中维护资源无限的情况下进行的.然而,在现实世界中维护计划通常受到资源可用性的限制.根据文献[7]可知:当多个组件通过共享备件、工具或维护人员连接时,就会出现资源依赖性.例如,如果系统由于工人的可用性有限而显示出资源依赖性,那么维护活动的同步调度将受到可用维护人员数量的限制.Charkhgard等[8]对MaxTFFAO进行了拓展,其基于使用的预防维护以网络路径的角度对该问题重新建模并进行了深入研究,探讨了在一条路径上的维护设备有限且唯一,同时该维护设备在单位时间段内可到达的弧的范围为有限的情况.在其研究中验证了即使只有一个设备需要维护,该问题仍是NP难的.

针对基于网络优化模型研究系统的设备维护调度问题,Urbani等[9]研究了将多组件系统建模为网络化的有向图,在其网络中节点表示机器或工人,边表示这些节点之间的材料、信息或工作交换.制定了一个双目标优化问题,该问题考虑了维修人员的有限可用性,目的是寻求最佳维护计划.冯乐乐[10]提出了一种基于设备健康指数的多设备生产线预防性机会维护方法.谢志强等[11]提出了基于动态规划调整设备维护开始时间的综合调度算法.

文中结合黄骅港作业实际场景的需求,考虑了维护资源配备组(维护人员和其他资源)的限制,构建了资源限制下的网络维护调度优化的混合整数规划模型,涉及维护作业的分配和时间表设计.该模型在MaxTFFAO问题结构上,增加了维护资源到维护任务的分配,具有带时间窗车辆路径问题的特征.通过基于问题结构的分解,提高了精确算法的求解能力,并在实际数据和测试算例中验证了方法的有效性.

1 问题描述及模型

1.1 问题描述

在黄骅港的生产场景中,火车将煤炭运送到港口后需要经过翻车机、堆料机、取料机、装船机以及设备间输送煤炭的皮带等运送到船舶,见图1.由于使用和暴露于环境的原因,港口的设备通常随着时间的推移会退化.这将导致设备的质量下降,最终导致设备故障.为了避免在设备突然发生故障后进行成本更高的事后维护,企业会对设备进行定期检查和保养措施的预防性维护.这也是确保了设备运转的性能和可靠性水平.

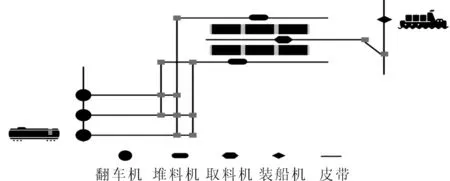
图1 煤炭港口装卸设备关联示意图

相互关联的港口设备组成了设备网络,可以抽象为图2的有向图来描述,其中V表示设备连接关系节点.网络中的弧a∈A分为设备弧和关系弧,其中设备弧代表的是一个设备.由于部分设备之间的相互关系复杂,因此需用关系弧进行表示.每个设备的单位运行效率为每条设备弧上的容量.对于关系弧的容量则等于其出发节点所连接的设备弧的容量.

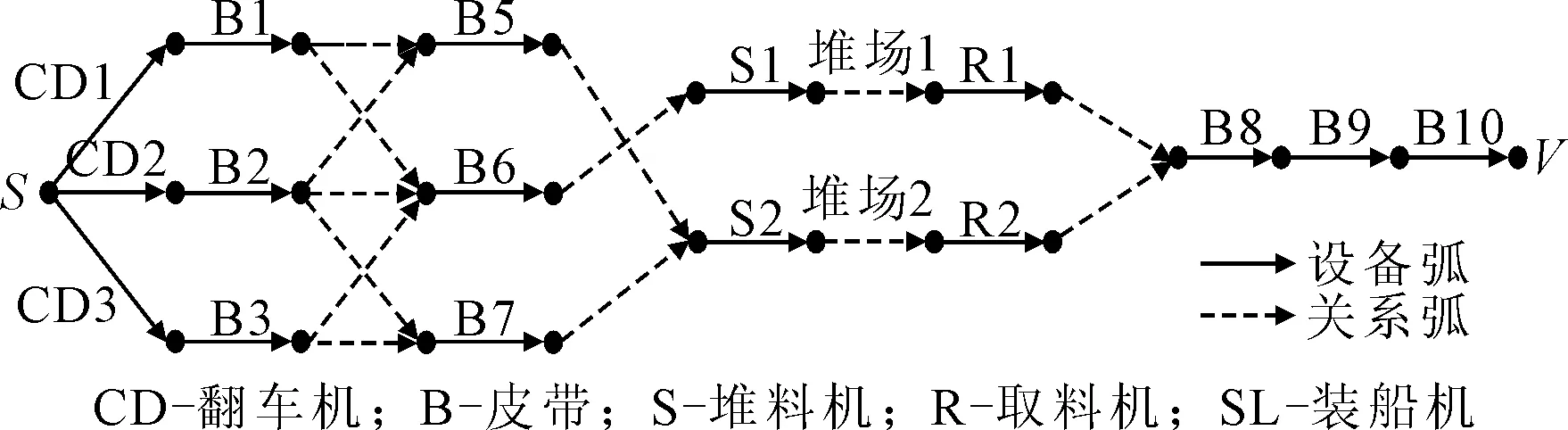
图2 设备网络有向图示意图

在港口日常运作时,维护计划通常受到资源可用性的限制.港口设备共享备件、工具和维护人员.因此维护活动的同步调度将受到可用维护人员数量的限制.此外,在开始执行维护作业之前,维护人员需申请流动机械和备件,以及一定的到达维修点的时间[12].因此同一维护人员的多个维护作业之间需要一定大小的时间间隔.

1.2 参数设置

定义设备网络G=(V,A),其中V为节点集合,A为有向的弧集.虚拟一个源点s和一个汇点v.其他具体的参数说明如下.

1) 参数集合δ+(v)为流出每个节点v∈V的弧集;δ-(v)为流入每个节点v∈V的弧集;J为所有维护作业的集合;Ja为单个弧上维护作业的集合.

2) 参数T为设备网络G的总规划期;Ca为每个弧上的容量;pj为每个维护作业的处理时间;rj为每个维护作业的最早开始时间;dj为每个维护作业的最迟截止时间;[rj,dj-pj+1]为每个维护作业的可以开始执行的时间窗;Tij为维护作业之间的维护人员到达时间间隔;K为维护人员的数量.

1.3 数学模型

将资源限制下的网络维护问题表述为MIP问题.该问题中要最大化的目标函数是在总规划期内设备网络的吞吐能力,即经过的流量最大.

(1)

该问题的可行方案由以下一组约束条件定义.

(2)

(3)

(4)

(5)

(6)

∀i∈J,k=1,2,…,K

(7)

(8)

startik+pi+Tij-M(1-wijk)≤

startjk,i≠j∈[J],k∈K

(9)

(10)

wijk∈{0,1},startjk≥0

(11)

式(2)和式(3)分别为t时段对应的每个弧流量出入平衡,且流经的流量小于弧的容量.式(4)为每个维护作业执行时相对应的弧会中断,且同一个弧上的多个维护作业不能同时进行.式(5)为每个维护作业只能有一个维护人员执行且每个维护作业的开始时间唯一.式(6)虚拟一个出发作业节点0.每个维护人员都会经过虚拟节点一次.式(7)限定了每个作业节点只能被一个维护人员访问一次.即如果维护作业j被维护人员k在其时间窗内执行,则等于1,否则为0.式(8)定义了每个维护作业的时间戳.式(9)为一个维护人员执行的维护作业之间必须有一个准备和到达所需的间隔时间Tij,该约束同为消除子回路约束.式(10)为资源约束.即同一时间网络中中断的弧的数量不能大于维护人员的数量.

2 Benders分解算法设计

2.1 Benders模型分解设计

Benders Decomposition与传统的Benders算法在子问题和主问题之间循环迭代求解不同,采用Branch and Benders Cut(B&BC)算法框架,是只需求解一次主问题的Benders分解算法.

该问题可以分解为两个问题,子问题为网络最大流问题,主问题为一个具有VRP特征的调度问题.

(12)

(14)

φat≥0

(15)

当子问题求解完后获取其对偶变量uat,并引入一个θt变量用以表示主问题的上界.

(16)

将式(16)加入主问题后主问题模型为

(17)

(18)

(19)

算法步骤为:

步骤1初始化参数G,A,T,C,J,Ja,K.

步骤2构建子问题模型和主问题模型,设置xat=1(∀a∈A,t∈[T]).

步骤3获取子问题目标值x0,构造约束θt≤x0加入主问题中.

步骤4设置主问题参数MipGapAbs=0.999,MipGap=1×10-6.

步骤5求解主问题,求解过程中利用求解器的Callback函数向主问题中加入Benders割.

2.2 网络最小割

因为关闭任意的弧都不可能增加网络总流量,所以当网络中的弧都处于连通状态,即xat=1(∀a∈A,t∈[T])时,网络可以通过的最大流量为网络流量的上界.与容量约束相关的非零对偶变量的弧集是来自最大流最小割定理的“最小割集”,最小割集是网络的瓶颈.因为最小割集中的任意弧的中断,都会直接影响通过网络的总流量.图3为分层结构示意图.

图3 分层结构示意图

除去虚拟的源汇点,该网络有两层,其中弧1～2的容量之和为10,弧3～4的容量之总和为15.在这种情况下,初始割集将为弧1～2.组成了最小割集即为网络的瓶颈,故可以在模型中增加约束.

θt≤4x1t+6x2t∀t∈T

(20)

由于这些弧为最大流量最小切割定理中定义的最小切割集,所以其是该网络的瓶颈所在.假设增加这些弧的容量,使其大于弧3～4的容量之和.然后我们再次求解这一最大流量问题时,发现第二个最小割集为弧3～4.然后只需在模型中添加瓶颈约束:

θt≤8x3t+7x4t∀t∈T

(21)

这些约束都是有效的.通过这些网络流瓶颈约束,可以找到满足调度约束的主问题的解决方案.当遇到分支和定界树的节点时,检查是否需要更多的网络流瓶颈割,以惰性约束的方式添加到模型中.该实施将被记为为网络最小割(Net-cuts).

算法步骤为:

步骤1检查子问题的对偶变量ua,∀a∈A.

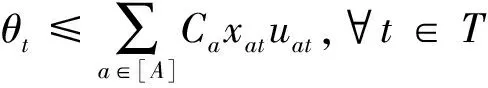
步骤3重置Ca,∀a∈A的值.

该算法步骤用于Benders算法步骤的3～4.

3 算例实验分析

3.1 算例测试集

实验数据由维护作业信息数据和网络结构数据两部分组成.网络结构数据是由黄骅港一期项目的现实场景抽象而来,关于场景包含的设备详情见表1.

表1 网络结构数据详情

维护数据主要的参数有维护任务可选开始时间窗、维护任务的处理时间.在生成测试数据时主要关注两点:时间窗的大小和处理时间的长短.很容易知道时间窗的大小对模型的求解规模影响极大.因此在生成测试数据时,生成了三种规模的时间窗.而处理时间的长短决定了网络中断的总规模.除了测试算例集,还依据港口生产的现实维护状态进行设计实例数据C进行测试.现实场景中维护任务往往会因为生产压力而推迟执行,因此每个维护任务的时间窗的规模往往较大.具体参数见表2.

表2 维护作业数据详情

3.2 算法性能对比分析

设定了以下对比指标.F-time为模型在迭代求解的过程中发现第一个可行解的时间;S-time为程序运行时间,采用此指标用以观察算法在寻优的表现.gap为每个资源下网络相应的求解gap值.

小规模时间窗下,模型整体规模较小.见表3算例A1的结果显示,Gurobi和B&BC都可以在极短的时间寻找到可行解.但在寻找最优解上,Gurobi明显优于B&BC.这是由于B&BC分解原模型的同时,丧失了相应的信息,从而B&BC在主问题获得的松弛解的质量比原问题差.这意味着B&BC的上界很差且产生了很多无效分支,增加搜索成本.算例B1相较于A1,增大了作业处理时间,这样会导致维护资源的需求增大,因此在资源为1时无解.

表3 算法运行1 800 s结果对比详情

中规模时间窗下,问题规模增大.通过算例A2和B2发现B&BC寻找可行解的优势更加明显.算例B2中,在资源为3和4时B&BC都寻到了可行解而Gurobi没有.特别在资源为5时,B&BC在找可行解和寻优上都优于Gurobi.这是因为B&BC将规模变大的原问题分解后,主问题的规模相较于原问题会小很多,在探寻节点的速度上更快.虽然其松弛解质量要比原问题差很多,但利用Callback加入有效Benders割可以对主问题的规模进行有效的消减.

大规模时间窗下,进一步验证了之前算法的表现.除此之外,在算例B3时发现资源为4时B&BC找不到可行解,而Gurobi可以寻到最优解.这和其它算例中B&BC在特定资源下寻找可行解不如Gurobi的原因相同.随着资源的增大,问题规模也随之增大.但是不同资源下的Benders割的有效性可能是相同的,对于效果一样的Benders割,问题规模却倍增下,寻找可行解的难度自然增大很多.

3.3 算法改进对比

从网络的分层结构出发,构造了网络最小割用以提高松弛解的质量.

在实际运用场景中,数据规模往往偏大.在表4实例数据C的求解结果看,B&BC和其改进在寻优和发现可行解方面的表现都远远强于Gurobi,符合3.2中分析的不同数据算法求解规律.在资源为1时Net-B&BC算法表现的非常优秀.其不仅在117.3 s内就求得了最优解,且在发现最优解的时间花费也是最少的.

表4 实例数据C算法运行1800s结果对比详情

表5列出了Root松弛解、添加cut数量和搜索节点数量的详细信息来说明B&BC和Net-B&BC两者的优劣.Net-B&BC的松弛解的质量明显全部优于B&BC,这意味着网络最小割十分有效.且在算法运行中Net-B&BC向主问题中添加的benders割的数目大量减少,这意味着网络最小割的加入有效的排除了大量的无效benders割的加入.而且分支定界树的规模相对变小,这在node数量的对比上可以有效体现.

表5 B&BC和Pre-B&BC算法运行信息详情

4 结 论

1) 建立资源约束下的网络维护问题整数规划模型,可以同时处理维护人员配置和任务调度两个维度的问题,更贴近工程实际需求.

2) 可以在规划期内同步为港口范围内所有部门的预防性维护任务制定统一的调度时刻表,相较于传统的分部门分时段的人工决策更有助于提升系统整体的作业效率,有利于洞察港口作业系统生产运营的薄弱环节.

3) 设计了基于网络数据结构的网络最小割进行算法改进.通过对真实作业数据和测试用例的计算实验分析了不同的维护任务数据对于问题求解难度的影响,验证了所提出的算法的有效性,尤其在某些算例中有非常优秀的表现.

后续研究将会考虑与启发式算法结合去改进算法以适用于更大规模的工业数据.除此之外,也会围绕该问题的本质结构进行更深入的探索,寻找更多有效的不等式以提升MIP模型线性松弛解的下界.