基于神经网络的高校贫困生辅助认定模型研究

曾文玄，高启文，陈新超

(1.福建医科大学 信息中心，福建 福州 350122；2.福建医科大学 后勤管理处，福建 福州 350122；3.福建医科大学 教务处，福建 福州 350122)

0 引言

新时期指导我国扶贫工作的重要思想是精准扶贫,“精准资助”也成为现阶段我国贫困生资助等教育扶贫工作的新任务[1]。作为贫困生资助的首要环节,贫困生认定涉及有效识别贫困生这一根本问题,是资助工作的重要基础,是促进教育公平的关键环节[2]。

目前,大多数高校的贫困生资格认定流程为:学生个人自愿填写家庭经济贫困申请表以及承诺书,附上地方政府出具的贫困证明一同交由班级评议小组民主评议,辅导员对申请资助的学生进行一对一谈话,最后对学生是否贫困进行综合判定。这类认定过程存在以下问题。

(1)经常出现“假贫困”现象。税收可以最直接、最客观和最准确地反映个人和家庭经济情况,但我国的收入申报制度和税收制度尚未完善,侧面了解公民的收入和家庭经济状况暂时无法完全实现[3]。而对学生家庭实地调查走访的成本太高,所以贫困生认定过程中过于依靠申报者的自律,容易出现虚假材料;而监督惩处开具虚假贫困证明行为的力度较弱,使得递交贫困证明的公信力下降,很难获取真实可靠的相关数据,贫困生认定中不可避免出现“假贫困”现象。

(2)真困难学生自我主动“屏蔽”贫困。在实际工作中发现,有很多家庭经济贫困的学生由于家庭具体情况、性格等原因,不愿意让同学知晓自己的家庭经济情况而放弃贫困资助,宁愿省吃俭用或者东挪西借也不愿意申报,自我主动“屏蔽”贫困[4]。

(3)认定工作受主观影响过大。在贫困生认定中,特别是班级民主评议小组评议过程中,普遍存在受主观影响较大、标准不够客观清晰、判定方法合理性不足和人为操作性较大等问题。

近年来高校信息化建设不断发展,已经进入“智慧校园”阶段。在大面积、长期覆盖的信息化环境中,高校建立的各业务管理系统积累了各类反映学生行为特征的海量数据,如生活消费一卡通数据、教务教学及综合测评数据和学工系统学生信息数据等[5]。这些数据都是学生现实生活的数字化表现,通过对其中包含的学生个人相关信息、在校学业情况和生活消费等数据进行分析挖掘,可以得到反映学生基本行为特征的精准数据,基于这些精准数据采用全神经网络进行学习训练,获得的高校贫困生辅助认定模型具有较高的预测能力,可以为智慧校园背景下高校贫困生认定工作提供更为精准、客观的支撑,较好地解决现有高校贫困生认定环节中存在的问题[6]。

1 原理

1.1 Tensorflow框架

2015年11月,谷歌发布第二代基于人工智能网络学习的系统——TensorFlow,它由 Google Brain团队开发和维护,是基于Python的开源机器学习框架。其本质是采用数据流图(Data Flow Graphs)进行数据分析和处理,将复杂的数据结构向复杂的人工智能神经网中传输。TensorFlow可以在只调用一个TensorFlow API的前提下将深度神经网络的计算部署到任意数量的CPU或GPU的服务器、PC终端或移动设备和网页上,实现多层级结构。TensorFlow 还可以提供除Python之外其他编程语言的接口,如Java、JavaScript、Go、R和C/C++ 等,可以应用在音频处理、推荐系统和自然语言处理和图形分类等各种场景,是深受市场欢迎的主流机器学习框架[7]。Tensorflow具有适用于多种开发语言、有各方面强大支持,具有高移植性,比Torch/Theano拥有更好的计算图表可视性。

1.2 全连接神经网络

人工神经网络(Artificial Neural Networks, ANNs)简称神经网络(NNs)或连接模型,是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的[8]。

一个全连接神经网络的结构,包含输入层(样本数据)、隐藏层(自己设定层数)和输出层(预测目标),一个神经网络结构只有一个输入层和一个输出层,输入层和输出层之间的都是隐藏层。每一层神经网络都有若干神经元,层与层之间神经元相互连接,且下一层神经元连接上一层所有的神经元,而层内神经元不产生任何连接[9],全连接神经网络结构如图1所示。

可设计一个最简单的神经网络来方便理解,它只有一个神经元,简单全连接神经网络的结构如图2所示。

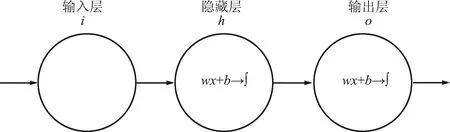
图2 简单全连接神经网络的结构Fig.2 Structure of a simple fully connected neural network

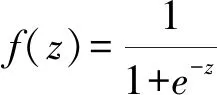
进行模型训练的目的是使神经网络的输出和实际的输出也就是标签一样,但出现这样的效果之前,二者之间存在一定的差异,将这个“差异”设为参数e,表示误差,模型输出加上误差之后即为真实标签,记作y=wx+b+e。

当有n个输入x和输出y,即有n个误差e。把n个误差e都相加,表示误差总量,为了避免残差正负抵消,可取平方或取绝对值,此处取平方。这种误差称为“残差”,是模型的输出结果和真实结果之间的差值,损失函数Loss还可以称为“代价函数cost”, 残差表达式如下:

模型训练的目的是找到合适的w和b,使得整个残差尽可能小,残差越小说明训练的模型越好[11]。

2 基于校园大数据环境下贫困生认定

2.1 贫困生辅助认定实现总流程

首先采集与贫困生相关的数据并进行处理得到数据集,将此数据集作为样本特征值输入进行模型训练,将是否为贫困生设置为模型的输出标签,神经网络基于输入的样本数据进行学习训练,根据学习到的知识(即模型)产生期望输出,再将期望输出结果与标签值进行比较,如结果和标签值一致则说明训练结果准确。模型训练结果有训练精度(ACC)和损失值(LOSS)参数,精度越高(损失值越低)表明模型的性能越高,预测的结果越准确。通过对初始参数的调整设置,学习模型进行反复迭代学习,不断地自我改进从而得到更高的精度,提高模型预测的能力。

功能的实现主要包含以下几个步骤[12]:

①从校园一卡通系统、学工系统和教务系统抽取不同年级各专业学生的消费数据、综合测评结果和个人家庭信息作为原始数据;

②清洗抽取的样本数据,将与贫困生认定无关的数据项剔除;

③预处理得到的数据集,将源数据进行数据标准化、规范化处理,以得到模型训练可用的数据集;

④利用样本数据集和标签数据,建立贫困辅助认定模型,模型训练得到预测模型。

贫困生辅助认定总流程如图3 所示。

图3 贫困生辅助认定总流程Fig.3 Overall flowchart for auxiliary identification of poverty students

2.2 实验数据建模

进行贫困生辅助认定模型训练,需要先准备好可训练的数据集作为训练的样本数据集,数据集的建模需经过以下几个过程:采集数据源、数据属性抽取、数据建模、数据均衡化、PCA因子分析和数据归一化。贫困生辅助认定的数据准备流程如图4 所示。

2.2.1 数据源及抽取

采用神经网络训练模型的过程中,首要关注的是样本数据(输入层)和标签数据(输出层),对应的是学生的基本行为特征和贫困生认定数据,本文主要从反映学生消费水平的消费行为习惯、在校学业情况(包括德、智和体各方面表现)、影响学生家庭经济情况的学生亲属情况和个人信息等方面考虑确定数据源,并从中抽取相关数据,结合往年贫困生认定数据作为实验样本数据[13]。

(1)一卡通消费数据

本文采集的某校一卡通数据包含了2016—2019级4个年级所有在校本科生2020年9月份的消费数据,包括学号、校园卡号、食堂消费金额、超市消费金额、消费时间、消费类别名称、消费类型码、卡序号、消费地点、钱包余额和消费笔数计数等48个字段,数据量共35万条。学生消费数据样例如表1所示。

表1 学生消费数据样例

从学生消费数据表中去除校园卡号、消费时间、消费类别名称、消费类型码、卡序号、消费地点、钱包余额和消费笔数等与学生消费行为习惯不相关的数据选项。抽取和模型相关的数据项包括学号、食堂消费金额和超市消费金额等数据。

(2)学生综合测评结果

2019—2020学年的学生综合评定情况包括学号、姓名、测评学年、学院、专业、班级、是否补考、现在年级、专业年级排名、综测总分、德育测评成绩、智育测评成绩、体育测评成绩、德育专业排名、智育专业排名和体育专业排名共16个字段,数据量共17.7万余条。学生综合测评结果样例如表2所示。

在综合测评结果表中,德育、智育和体育成绩已经细化体现了综测总分,所以去除学生综测总分;保留比德育、智育和体育成绩更有相对可比性的各项专业排名数据;去除与学业情况无关的学院、专业、班级、姓名和年级等数据;由于只采用一个学年的测评结果,将测评学年去除。最后从学生综合测评结果表中抽取学生德育、智育和体育成绩专业排名,专业年级排名、是否补考等数据项。

(3)学生亲属关系表

主要是对学生的亲属关系描述字段,包括学生学号、与本人关系、学生姓名、学生性别、亲属姓名、亲属性别和亲属婚姻情况共7个字段,数据量共14.5万余条,学生亲属关系样例如表3所示。

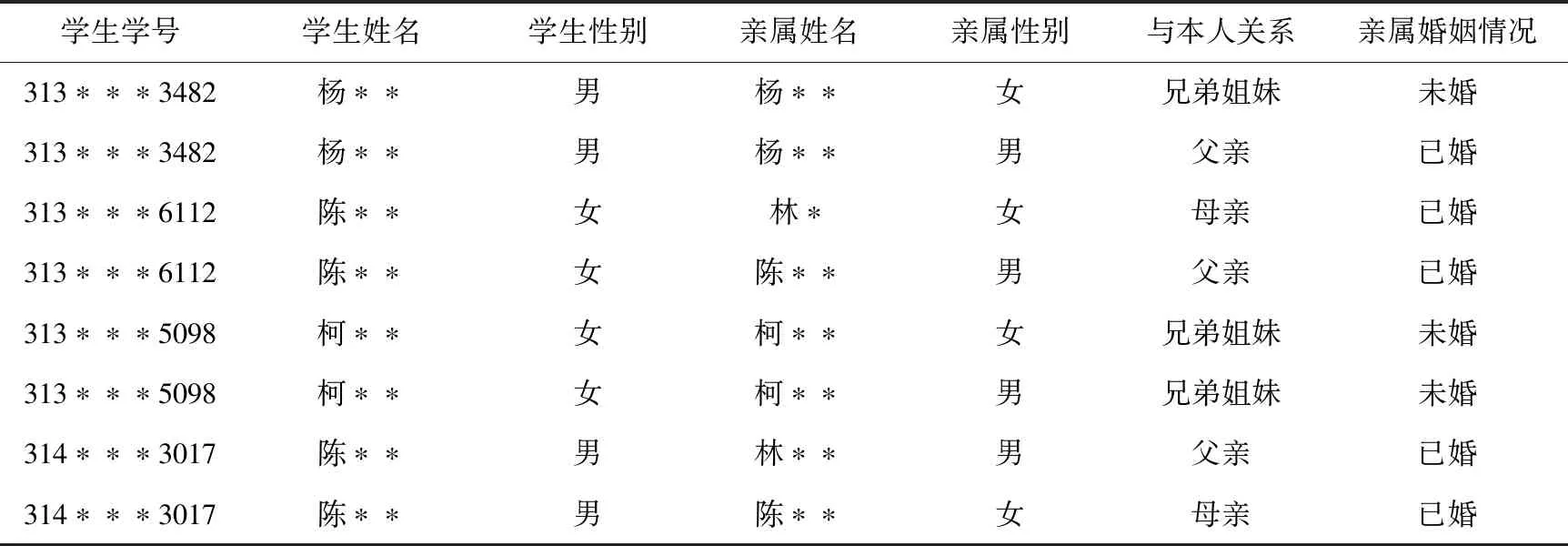
表3 学生亲属关系样例Tab.3 Sample table of student family relationship

在亲属关系数据中,与本人关系字段反应出亲属是否健在,亲属是否健在是影响学生家庭经济情况的重要因素,所以抽取与本人关系和学生学号2个数据项作为训练数据。

(4)困难生认定信息表

2019—2020学年困难生申请信息包括审核状态、学号、姓名、院系、现在年级、申请时间、评定学年、申请困难类型和评定困难类型共9个字段,数据量共2.6万余条。困难生认定信息样例如表4所示。

本文中2019—2020学年困难生认定信息表的数据主要作为模型的样本数据使用。出现在此表中的均为贫困生,抽取可判断出是否贫困生的学号、评定困难类型2个数据项作为训练数据。

2.2.2 数据处理及标准化

前文从多数据源抽取的相关数据量较大,但并不是所有数据对于贫困生认定模型训练都有意义。为了保证训练结果可靠、使数据具有更强的泛化能力与适应性,在进行模型训练之前需将抽取的大量数据中有价值的部分挖掘出来,对数据进行清洗降噪、分析和整合等处理,并将数据转换,完成数据的标准化,得到模型可训练的数据集。

①将抽取的消费数据按照学号统计出学生在2020年9月份的消费总金额,将数据泛化。

②抽取的综合测评结果数据中,以7开头的专升本学生数据中的年级专业排名数据中,排名有大量并列第一的情况,不具备参考性,予以清除。

③将亲属关系数据中与本人关系数据项进行建模,按照学号对应,此数据项值为兄弟姐妹的转换为是有兄弟姐妹值为1,否则值为0[14];数据项值为父亲的转换为父亲健在值为1,否则值为0;数据项值为母亲的转换为母亲健在值为1,否则值为0。

④用2019—2020学年困难生认定信息和消费数据表数据,通过逻辑判断来确定是否贫困生这个标签值。在消费数据表中增加是否贫困生数据项,如果学生学号在贫困生认定表中出现,其对应为贫困生数值为1,否则为0。

将以上处理后的数据表通过学号这一字段关联整合成一个贫困生辅助认定训练数据集,数据集共有8 900余条数据。贫困生辅助认定训练数据集如表5所示。

表5 贫困生辅助认定训练数据集Tab.5 Training dataset for auxiliary identification of poverty students

⑤数据均衡化

为了保证模型训练结果的可靠性,在不破坏原数据之间相对关系的前提下获得更合理的数据集分布,需要对消费数据进行分布均衡化处理。

经以上处理后的数据集共有8 902条数据,包含了6 571条非贫困生数据和2 331条贫困生数据,正负样本的比例为1∶3。为保留一定量的正向样本,将贫困生消费数据分布中的离群值剔除,留取1 552条贫困生样本数据,剔除后贫困生的月消费金额为0～900元,剔除的贫困生数据作为测试集使用。之后将非贫困生消费数据分布中的离群值剔除,因为正向样本的比例偏少,所以根据欠采样的方法,在学生月消费金额为0～900元的非贫困生中抽取一定量数据,使正负样本比例接近1∶1,最终随机采样非贫困生消费数据1 613条[15]。

均衡前后学生月消费数据分布对比如图5所示。蓝色折线横坐标跨越0～1 600分布,说明均衡前学生的月消费金额在0～1 600元均有分布,而且不均匀:月消费金额在1～100元有2 182个学生,而月消费金额在1 200～1 300、1 300～1 400、1 400～1 500、1 500～1 600元各个区间的分布学生数均为个位数;均衡后橙色折线横坐标跨越0～900,说明学生月消费金额分布在0～900元的各个区间,橙色折线分布在整个图纵向的下半部分,说明每个区间的学生分布数量相差不大。对比分析可见,均衡化后学生消费数据分布更加均衡。

另一方面,也可以通过计算学生消费数据分布的标准差来观察均衡效果,学生消费数据分布均衡前后标准差如表6所示。由表6可以看出,学生消费数据分布均衡前后标准差从651.224 5降为281.268 8,说明均衡化效果较好。

⑥数据归一化

数据归一化方法一般是指将数据处理为[0,1]的实数。如学生月消费金额为20～700元,将其除以 1 000,即可实现归一化为[0,1][16]。

对于每一个维度指标,令 min(x(j))和 max(x(j))分别为数据集的最小和最大指标值[17],可得尺寸参数x(j)为:

因此,每个记录的值被映射到 [0,1]。利用(x(i),y(i)(i=1,2,…,q)规范化数据集,归一化指标向量为x(i)∈R。

具体的归一化算法实现如下:

scaler =MinMaxScaler()

scaler.fit(x_data) # 训练

x_data = scaler.transform(x_data) # 此时输出数组了

# print(x_data)

⑦PCA因子分析

通过PCA因子分析对数据进行降维度,做回归分析,降维算法实现如下:

pca_model = PCA(n_components=9).fit(x_data) # 代表提取的主成分有9个特征

x_pca_data = pca_model.transform(x_data)

print(x_pca_data)

2.3 模型训练

2.3.1 实验环境

软件环境:Python 3.6;CUDA 9.0;Tensorflow 2.4.0;Pandas 1.1.3。

硬件环境:macOS Catalina 10.15.7;Intel(R) Core(TM) i7-8569U CPU@ 2.80 GHz。

2.3.2 模型构建

由于预测的结果只有是否为贫困生,没有对贫困生进行分类,3 163条数据量并不大,所以此处采用的是较为简单的浅神经网络,模型包含3层(输入层、隐藏层、输出层),描述如下:

①输入层是9个维度的特征值,数据矩阵的大小为[n,9];

②隐藏层是2个全连接的ReLU层,每个ReLU层有64个神经元;

③输出层只有2个输出值:0或1,表示是否是贫困生。

具体的模型结构如图6所示。

2.3.3 训练参数

在算法模型训练之初需要对模型的训练参数进行初始化,主要包括学习率(lr)[18]、迭代次数(Epochs)[19]等。模型进行训练的过程中,对比各个参数设置不同值的训练结果,得到最优设置参数。

(1)在其他参数值相同的情况下,分别将学习率设置为0.1、0.01和0.001。当学习率设置为0.1时,ACC趋于80.45%收敛,ACC和LOSS的收敛效果均不理想;当学习率设置为0.01时,ACC趋于93.28%收敛,但LOSS的收敛效果不佳;当学习率设置为0.001时,LOSS趋向于0.1629 收敛,ACC趋向于93.14% 收敛且收敛效果好。不同学习率训练过程对比如图7所示。

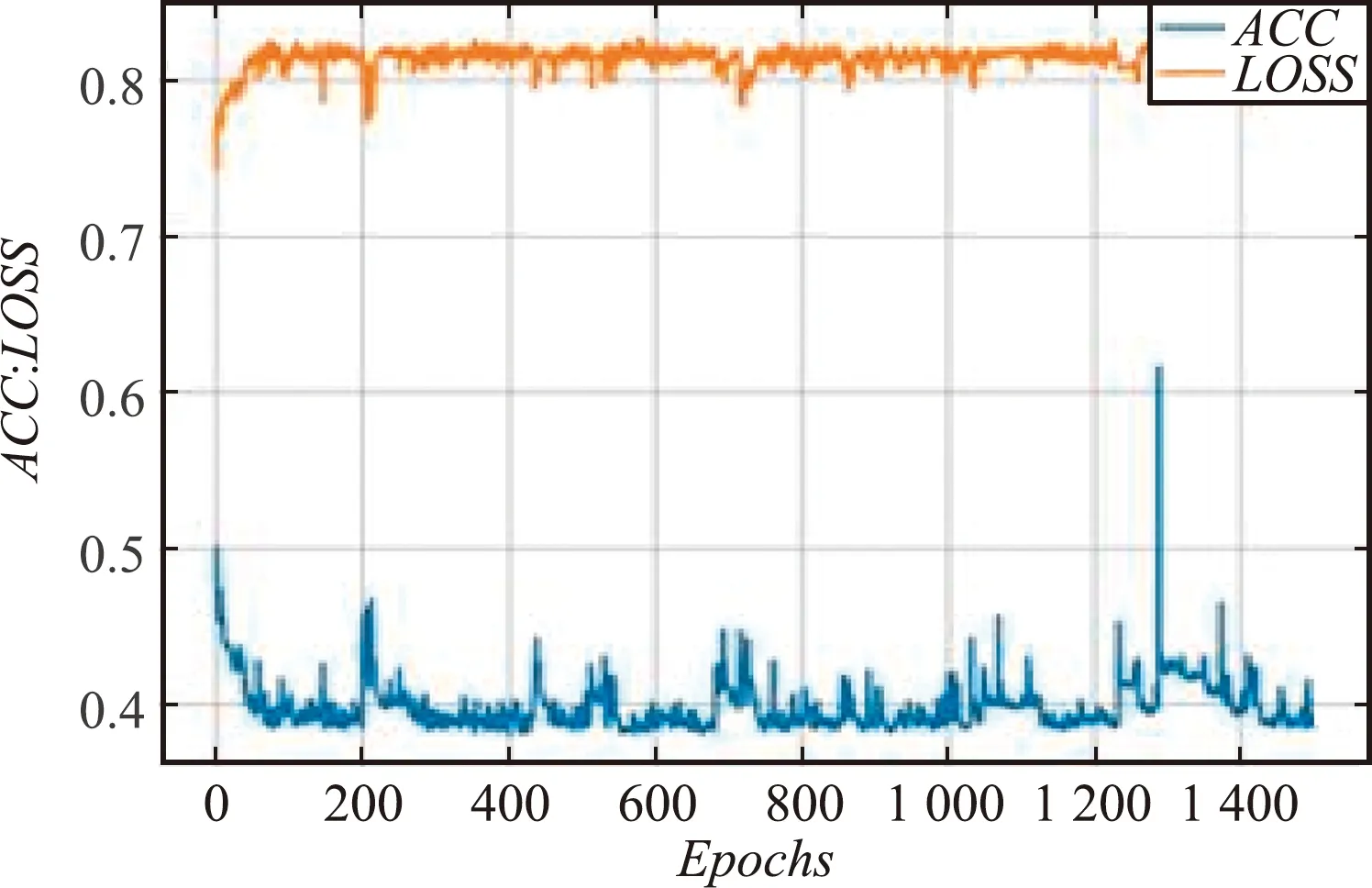
(a)学习率为0.1的训练过程

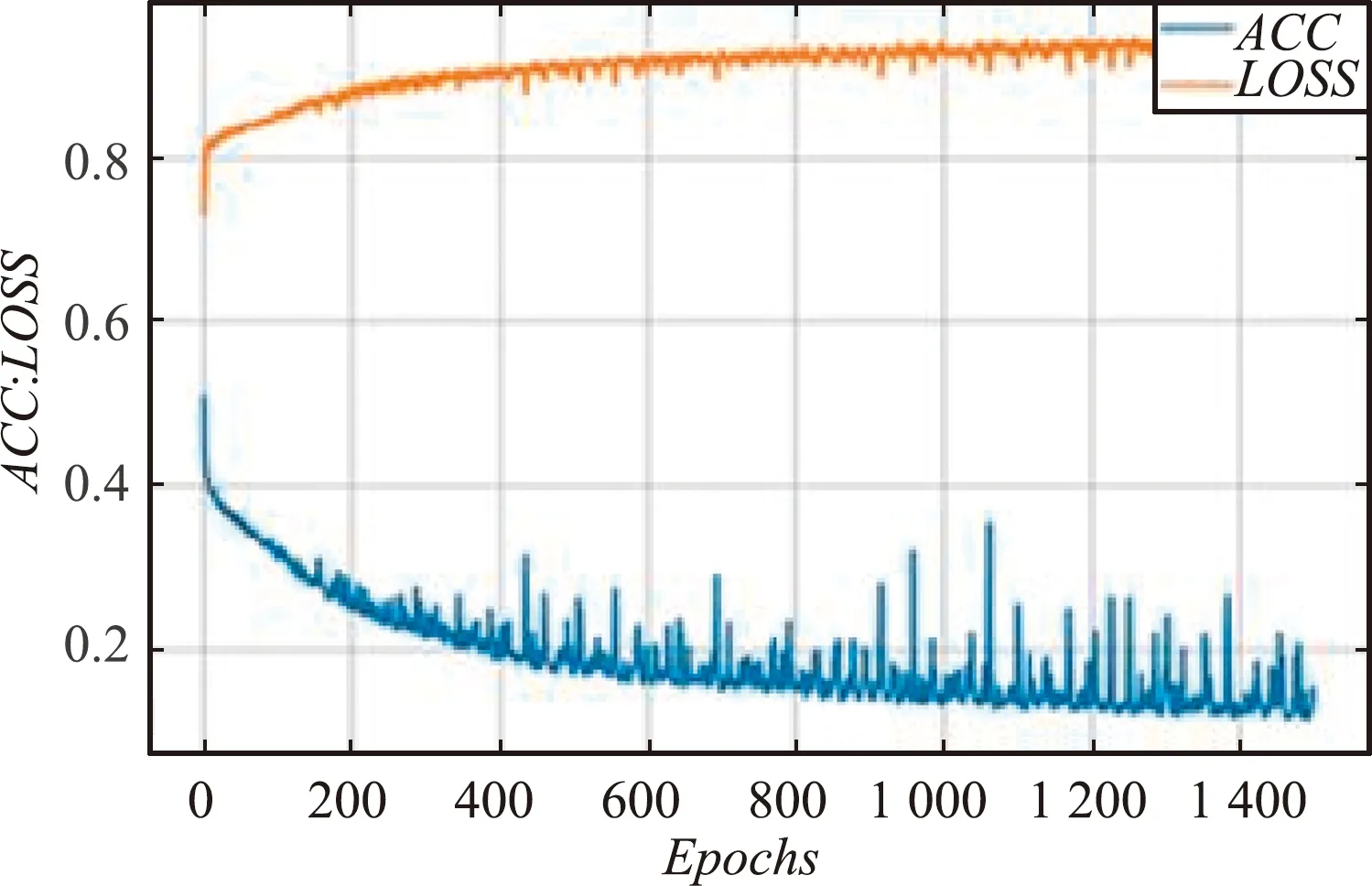
(b)学习率为0.01的训练过程

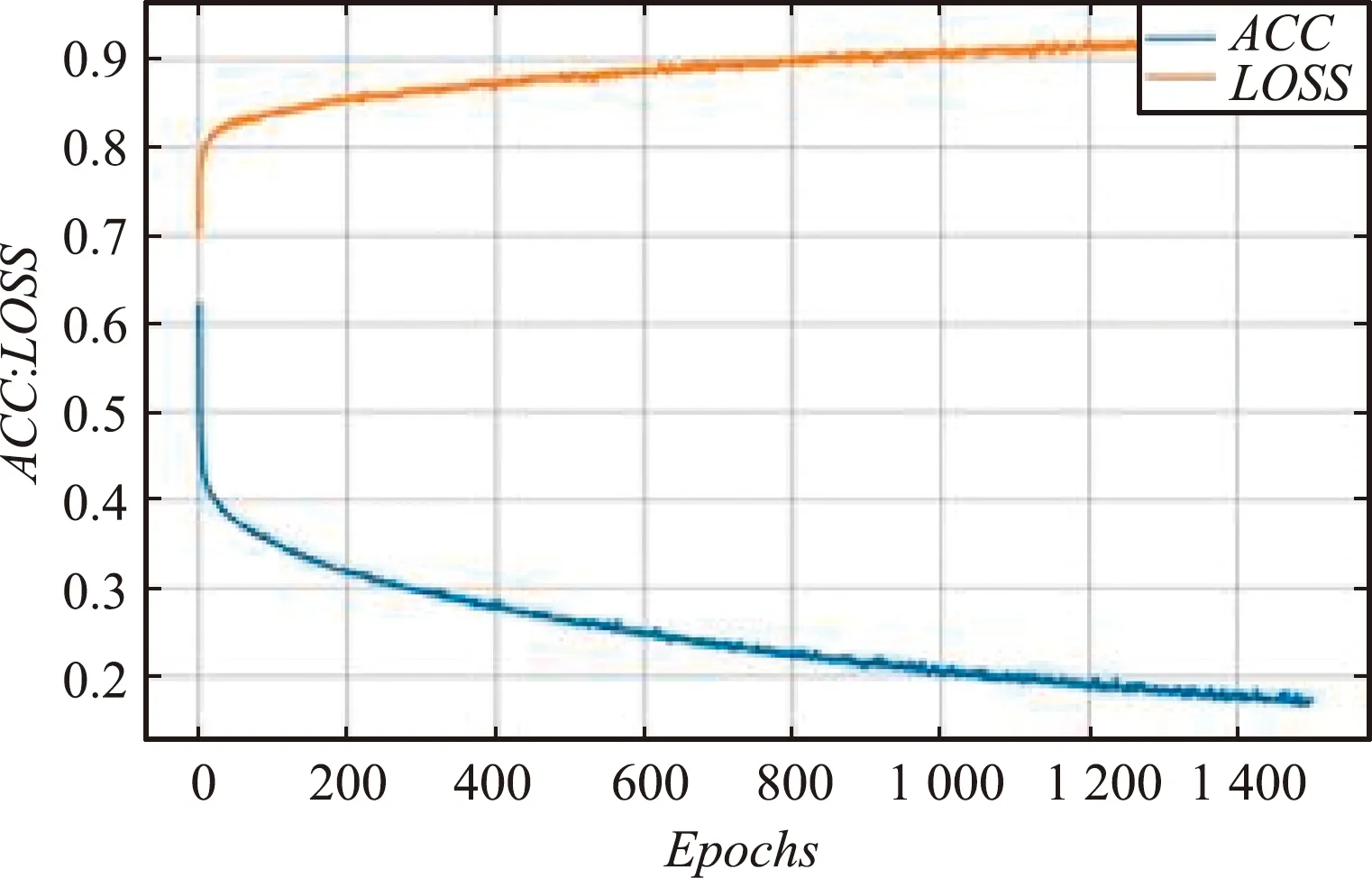
(c)学习率为0.001的训练过程

对比分析发现,迭代次数为1 500时,学习率为0.001的ACC值最高,收敛效果最好,模型的性能最好。不同学习率训练过程数据对比如表7所示。

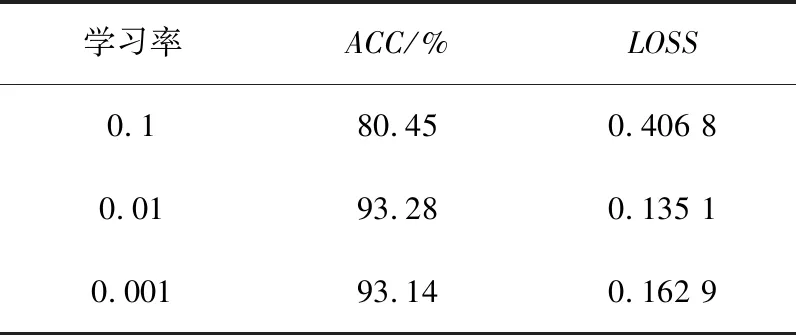
表7 不同学习率训练过程对比Tab.7 Comparison of training process with different learning rates

(2)在其他参数值相同的情况下,分别将迭代次数设置为1 500、5 000和10 000。当迭代次数设置为10 000时,ACC和LOSS的收敛效果均不理想;当迭代次数设置为5 000时,ACC趋于96.38%收敛,但是LOSS的收敛效果不佳;当迭代次数设置为1 500时,LOSS趋向于0.162 9收敛,ACC趋向于93.14%收敛。不同迭代次数训练过程对比如图8所示。

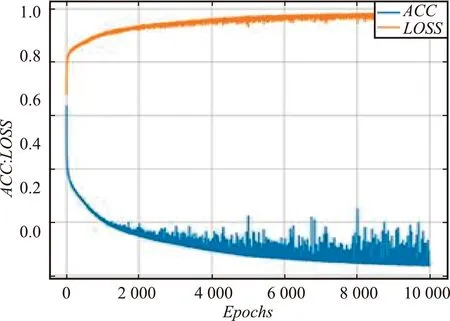
(a)迭代次数为10 000的训练过程

(b)迭代次数为5 000的训练过程

综合对比分析发现,迭代次数设置为1 500时模型的性能最好。不同迭代次数训练过程数据对比如表8所示。

表8 不同迭代次数训练过程对比Tab.8 Comparison of training process with different iterations

综合2个训练过程的对比,模型训练的主要参数学习率设为0.001,迭代次数设为1 500。

2.3.4 模型算法

本文的模型算法实现如下:

(1)模型搭建

model =tf.keras.Sequential([

tf.keras.layers.Dense(64, activation=‘relu’, input_shape=(9,)), # 9维数据

tf.keras.layers.Dense(64, activation=‘relu’), # 每层隐藏层64组神经元

tf.keras.layers.Dense(1, activation=‘sigmoid’) # 激活函数

])

print(model.summary())

plot_model(model, to_file=‘model.png’)

(2)编译与训练,本模型使用的损失函数是binary_crossentropy

model.compile(loss=‘binary_crossentropy’,

optimizer=keras.optimizers.

Adam(lr=0.001),

metrics=[‘acc’]) # 设置学习率

history =model.fit(x_pca_data, y_data, epochs=1500) #设置迭代次数

hist =pd.DataFrame(history.history)

hist[‘epoch’] =history.epoch

(3)绘制损失函数和准确率图像

def plot_his(hist):

migtime = hist[‘loss’]

delay = hist[‘acc’]

fig, ax =plt.subplots()

plt.xlabel(‘Epochs’)

plt.ylabel(‘ACC; LOSS’)

"""set interval for y label"""

yticks = range(10, 110, 10)

ax.set_yticks(yticks)

# """set min and max value for axes"""

#ax.set_ylim([10, 110])

#ax.set_xlim([58, 42])

x = hist["epoch"]

plt.plot(x, migtime, "-", label="ACC")

plt.plot(x, delay, "-", label="LOSS")

"""open the grid"""

plt.grid(True)

plt.legend(bbox_to_anchor=(1.0, 1), loc=1, borderaxespad=0.)

plt.show()

2.4 实验结果分析

基于学生消费数据的贫困生认定模型训练过程如图9所示。由图9可以看出,随着迭代次数的增长,模型训练LOSS和ACC均趋于平滑趋势[20],当迭代次数超过1 500后,LOSS趋向于0.162 9收敛,ACC趋向于93.14%收敛。

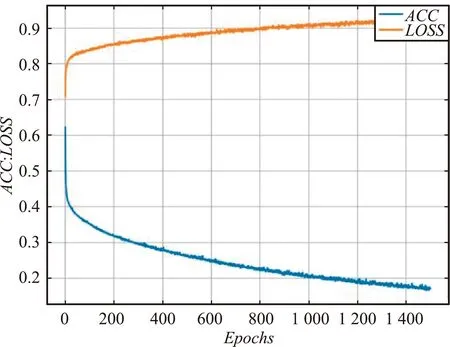
图9 贫困生认定模型训练过程Fig.9 Training process of identification model for poverty students

随机抽取20个测试集数据进行测试,测试准确率为90%,说明此模型的预测准确率较高,将此模型应用于贫困生判定,可以得到较为精准的结果。预测过程示意如图10所示。

图10 预测过程示意Fig.10 Prediction process

3 结束语

教育扶贫工作进入新阶段,大数据、人工智能等新技术给新时期的高校资助工作带来新的解决方案。本文利用智慧校园积累的海量学生数据和数据挖掘技术,深度学习训练获得的高校贫困生认定模型,预测准确度较高,为传统的贫困生认定方式提供了更为客观的支撑和有效补充,对于实现高校的“精准资助”和推进高校的管理工作具有一定的研究意义。但由于条件和时间有限,本文仅从是否为贫困生的角度去训练辅助认定模型,未考虑贫困生认定等级分类问题,更为精准的认定模型仍有待后续探索和深入优化研究。