基于静力修正的钢管混凝土拱桥Pushover法

谢开仲 ，梁栋，祝通华，覃悦

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 防灾减灾与工程安全重点实验室，广西 南宁 530004)

近年来，钢管混凝土(Concrete-filled Steel Tube,CFST)拱桥[1]发展迅速，目前，最大跨径已达575 m(平南三桥)，ZHENG 等[1-3]认为建造700 m 级的钢管混凝土拱桥已不存在技术门槛，使钢管混凝土拱桥成为500～1 000 m 跨径的优势桥型，前景广阔。跨径的增大使得钢管混凝土拱桥对抗震性能要求更高，而目前其在抗震方面的研究仍有不足[1]。当前主要抗震计算方法有静力非线性分析方法(Nonlinear Static Procedure)，即Pushover 分析方法、非线性时程方法和反应谱方法。其中反应谱方法仅适用于弹性分析，非线性时程方法难以快速评估，而Pushover 方法可以给出强震下结构的目标位移[4-5]，实现结构抗震性能的快速评估，因此得到广泛应用。该方法可研究结构单一、多向以及多向耦合地震作用的抗震性能[6-11]，如樊健生等[9-11]的研究表明多向以及多向耦合地震下Pushover方法运用的可行性。其次，Pushover方法可分析单一振型[12-15]以及多阶振型[16-19]影响的地震效应，其中，ROOSHENAS 等[16-17]基于能量原理、郝润霞等[18]基于拟力法、QU 等[19]基于振型刚度考虑高阶振型的影响，使Pushover 方法得到完善和发展。另一方面，在桥梁领域Pushover 方法多集中研究桥墩的抗震性能[20-22]，对于拱桥的抗震性能研究相对较少，且石拱桥[23-24]、钢拱桥[25-27]居多。由于大跨度钢管混凝土拱桥振型数量庞大，少数振型计算的精度得不到保证。对于Pushover 方法在钢管混凝土拱桥的适用性研究，申现龙等[28]针对下承式钢管混凝土拱桥采用模态Pushover 方法、上界Pushover方法与非线性时程分析方法对比分析，但其研究的重点仅限于桥墩的弹塑性性能；曾森等[29]采用模态Pushover 方法研究了钢管混凝土拱桥，表明考虑多阶振型模态Pushover 方法能得到更合理的结构最大响应结果。谢开仲等[30]研究了传统Pushover 方法在大跨度劲性骨架拱桥中的适用性，指出对于拱桥的不利截面可采用Pushover 方法进行抗震评估。文献[23-30]针对拱桥的Pushover 分析，多采用传统Pushover 方法进行，该方法一般假设结构的地震反应受第1阶振型控制，无法明确侧向荷载分布形式，考虑高阶振型时控制点选取困难、评估效率不足，当结构振型数量庞大时，如大跨度钢管混凝土拱桥，计算精度难以保证。因此，亟需一种计算精度较高且计算简单的拱桥Pushover方法。基于此，本文提出基于整体位移的能力谱模型，根据动力贡献系数提出高阶振型遴选方法，并结合静力修正方法提出了钢管混凝土拱桥Pushover法，解决传统Pushover方法无法明确侧向荷载分布形式、高阶振型选控制点困难等问题，同时通过静力修正提高求解的精度。采用该方法与现有文献结果对比验证其准确性，再对某钢管混凝土拱桥进行抗震评估。

1 钢管混凝土拱桥Pushover方法

1.1 基于整体位移的能力谱模型

采用黏滞阻尼的多自由度体系运动方程的一般形式为

式中：M，C和K分别表示结构的质量矩阵、阻尼矩阵、刚度矩阵，均为N×N阶矩阵；N为结构自由度数目；I为单位矩阵；为地震加速度。

将式(1)转化为单自由度的形式，令u=ϕnqn，并左乘，整理后可以得到

采用Pushover 方法求结构的能力谱曲线，其水平荷载分布模式应能反映结构在地震作用下真实的位移响应，从而更好地反映结构的地震破坏机理。工程中应用较多的有均匀分布、倒三角分布、抛物线分布、1 阶振型分布、等效基本振型分布和振型组合分布等分布荷载模式[30]。能力谱曲线按式(3)计算：

式中：表示第n振型的参与质量；Гn表示第n振型的参与系数；表示第n振型控制点i的位移；ui表示控制点i的位移增量；V表示基底剪力增量。

式(3)为传统求解能力谱模型的方法，分析时需要确定一个控制节点反映结构的位移响应。对于大跨度拱桥，不同振型选择控制节点较为复杂，较高阶振型由于多为空间弯扭变形，选取控制节点时会存在不合适[19]或者在加载初期和加载后期的变形方向不同而导致节点往复，得不到正确的能力谱。另一方面，传统Pushover 方法采用不同的分布荷载模式求解时，计算结果也不同[30]，如图1所示。采用不同的分布荷载模式得到的能力谱模型不同，可以迭代求解出不同的性能点，但何种分布荷载模式较为合适难以统一。因此，需要构建新的能力谱求解模型，解决传统Pushover 方法在钢管混凝土拱桥中运用的不足。

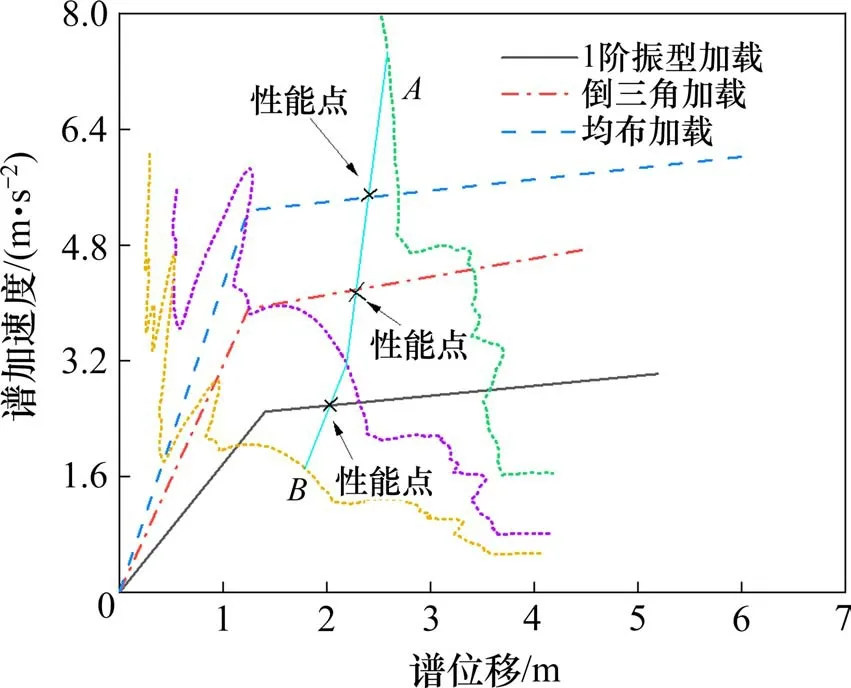
图1 传统方法的求解过程Fig.1 Solution process of traditional method

假设为地震荷载，取u=ϕnqn(t)=ϕnГnDn(t)，式(1)可以整理为

假设荷载形式为

式中：λ为荷载因子。

可以根据式(4)～(5)建立能力曲线。考虑到加载形式与振型相关，结构的节点位移也与振型相关，将u=ϕnГnDn左乘，采用矩阵形式求解能力谱曲线。其中An和Dn可以按式(6)进行计算：

式(6)采用矩阵求解，考虑了结构整体的位移，避免了高阶振型选控制点的困难，替代传统方法以单一控制点反映结构位移的能力曲线。有明确的加载模式F=λMϕn，避免了盲目选择侧向荷载形式带来的误差。根据式(6)得到能力曲线后，可以根据反应谱求性能点或采用时程分析求解式(4)得到谱位移，进而求得结构位移。

1.2 位移矩阵的静力修正方法

根据等效单自由度体系模型求得振型的广义坐标，经转化成几何体系坐标，各阶振型组合即得结构总动力响应。然而大跨度拱桥的振型数量是庞大的，对每一阶振型求解较为困难，可以用静力修正方法[31-33]对振型数量进行缩减。根据静力修正方法，结构的位移矩阵可以表示为：

其中，u表示结构的位移矩阵；m表示结构受动力放大效应影响较大的振型数量；ϕn为振型向量；q为振型的广义坐标，为便于区分将qnd表示动力求解值、qns表示静力求解值；K，M和I分别为结构的刚度矩阵、质量矩阵和单位矩阵。

在荷载频率一定时，随着考虑振型的频率提高，频率比趋向于0，结构的抗力趋近于纯静力而惯性力贡献几乎为0。采用式(7)可以提高计算精度，高阶振型通过静力修正，避免对高阶振型向量求解。借助所建立的能力曲线，根据式(2)不考虑惯性力和阻尼力得到

式(8)中，将替换为Dn/An即可得到非线性阶段的静力解qns：

在式(10)中，第1 项根据建立的等效单自由度体系，建立相应的恢复力模型得到qnd(t)；第2 项对结构静力分析得到-K-1(t)，求解过程应考虑结构的非线性；第3 项可以根据振型参与系数Гn，谱位移Dn，谱加速度An和地震加速度(t)直接计算得到；最后叠加得到结构的位移响应。

由于实际上更关心地震反应的峰值，振型的正交性可采用平方和开方法(SRSS)获取最不利值。由于拱桥与框架结构的不同，其抗震评估仅依据位移是不全面的，还需根据内力评估结构的屈服状态以及稳定性。而结构的位移响应是对各阶振型叠加后得到，对于结构的内力响应仍无法获得，因此需要建立结构内力求解模型，根据结构的刚度矩阵与恢复力的关系按式(11)计算

式中：F为外荷载矩阵。

式(11)中高阶振型的计算通过静力修正得到，降低了高阶振型的截断误差影响，保证计算的精度。为方便，把以荷载F=λMϕn对结构进行推覆分析，得到结构位移响应的过程称为1 阶段Pushover 分析；把以式(11)进行加载求解结构内力的过程称为2阶段Pushover分析。

1.3 钢管混凝土拱的评估指标

2 阶段Pushover 分析可以得到结构内力，为进行抗震评估需建立钢管混凝土拱评估指标，其主要受力如图2 所示。CFST 拱肋的受力较为复杂，应综合考虑钢管混凝土的套箍效应，引入轴力和弯矩组合系数λxg，表示拱肋的强度评估指标系数。其中λxg=0表示单元无损伤；λxg=1表示单元已破坏，计算如式(12)：

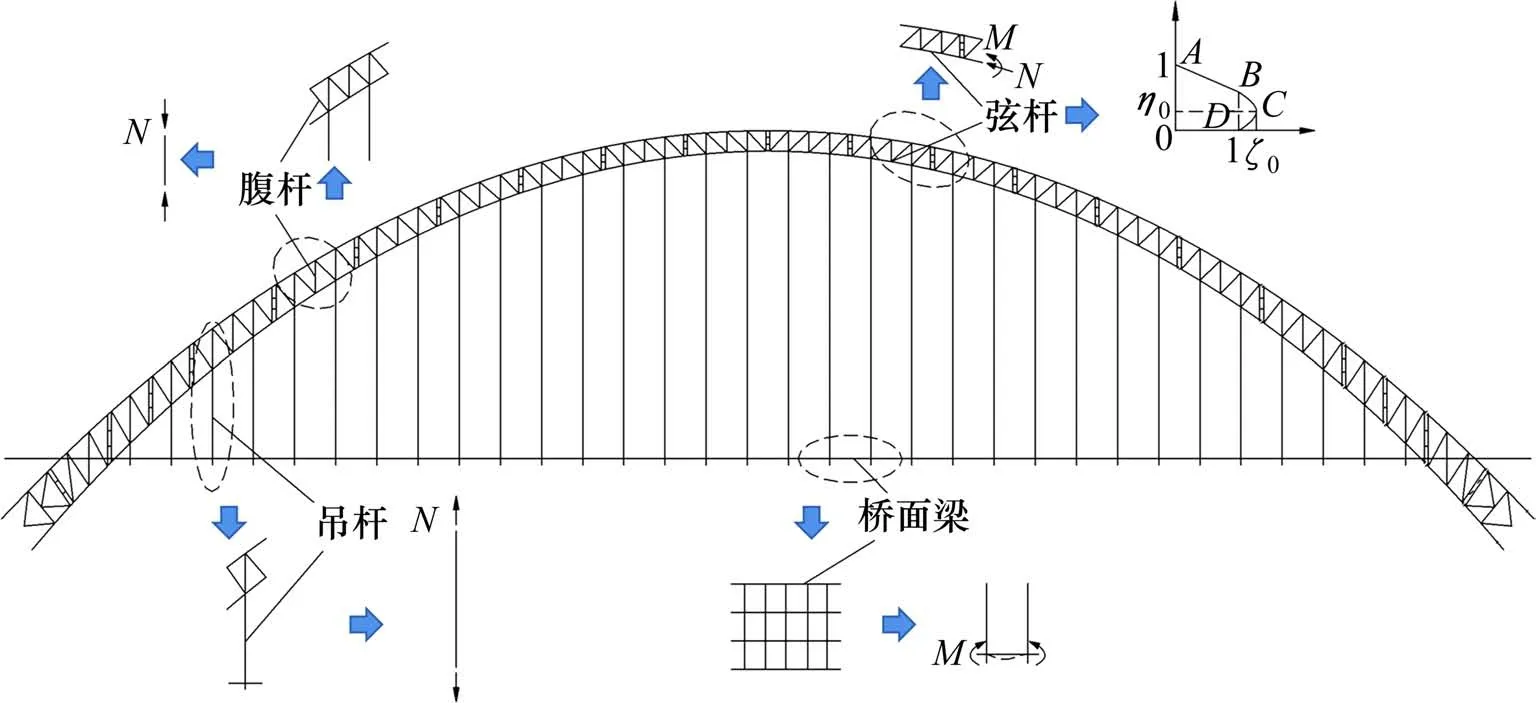
图2 钢管混凝土拱的主要构件受力简图Fig.2 Stress diagram of main components of CFST arch

1.3.2 钢管杆件

在地震作用下腹杆主要为拉压破坏，可根据其受力特点建立强度和稳定性指标：

式中：λy为强度指标系数；λcr为稳定性指标系数；σ和σs分别为钢管的应力和屈服应力；N和Ncr分别为钢管的轴力和临界轴力，，E为弹性模量；I为截面惯性矩；l为杆件的长度。

1.3.3 吊杆和桥面梁

吊杆属于拉压破坏，主要为强度破坏，评估系数定义为

式中：λyd为吊杆的强度指标系数；N和Nu分别为吊杆的轴力和极限轴力。

对测量模型信效度的检验发现：(1)各个潜变量具有较好的内部一致性，其内部一致性系数均在0.7以上，说明测量模型信度达到检验标准的要求；(2)所有显变量的因子载荷都大于0.5，这表明显变量和潜变量之间的从属关系在统计学上达到显著；(3)职业希望自我、心理弹性和主观幸福感三个潜变量的组合信度(CR)为0.7～0.84，全部大于0.7，平均方差提取值(AVE)也均大于0.4，说明测量模型的收敛效度通过检验。两个模型的拟合指标如表2所示。

桥面梁主要为弯曲破坏，评估系数定义为

式中：λyl为桥面梁的强度指标系数；M和Mu分别为梁的弯矩和极限弯矩。

1.4 基于动力贡献系数的振型遴选方法

不同振型对结构反应的贡献是不同的，可以根据振型贡献进一步缩减振型数量，提高计算效率。振型贡献指标有振型参与系数和动力放大系数，对于轴力型构件如拱结构[34]，振型参与系数指标会产生较大误差，振型恢复力响应得不到有效的评估。由于静力修正方法是基于振型的动力放大系数考虑的，故对振型遴选可以根据动力放大效应进行。根据式(2)，结构动力贡献部分为

则动力参与功为

振型的动力贡献系数

式中：δdn为第n振型的动力贡献系数；Гn为振型参与系数。

式(18)可以看出，动力贡献系数反应了结构动力响应的惯性力贡献，考虑所有的振型时，动力贡献系数等于质量参与系数，可以表示振型的动力放大效应，与静力修正方法的原理相对应。采用动力贡献系数进行振型的遴选，阈值按式(19)计算确定

式中：δdn(j=i)表示遴选的第i振型的动力贡献系数；δ为振型遴选的动力贡献系数阈值。

式(19)可以确定振型的阈值，遴选出动力贡献较大的振型，在遴选振型总数较少的情况下可以考虑更高阶振型，如前50 阶振型的累积动力贡献系数达到了90%，传统反应谱方法只考虑了前50阶，但是第55 阶振型比第40 阶振型的动力贡献系数大，而本文方法却可以考虑到，且振型的总数远少于50。再结合静力修正方法，使计算的振型数量大为减少，其累积动力贡献系数达到90%，保证了计算结果的可靠。

1.5 求解步骤

基于静力修正的钢管混凝土拱桥Pushover 法应用的一般程序为：

1) 根据结构的特点和材料属性，计算钢管混凝土拱构件的强度Nu，Ncr和Mu。

2) 建立空间有限元模型，进行模态分析获取模态数据，包括频率，振型参与系数Гn，振型向量ϕn和动力贡献系数δdn。

3) 根据式(19)确定振型贡献的阈值δ，遴选出需要叠加计算的振型。

4) 以荷载F=λMϕn对结构进行1 阶段Pushover分析，提取每一荷载步中荷载因子增量Δλ和各节点的位移增量Δu，然后按式(6)计算A和D，绘制能力谱曲线，建立等效单自由度体系模型。

5) 根据建立的等效单自由度体系模型求解式(4)，得到广义坐标qnd(t)，按式(9)计算静力解qns(t)，同时获取结构的静力解，再根据式(10)求原结构的位移响应。

6) 按式(11)加载进行2 阶段Pushover 分析，得到结构内力响应，根据式(12)～(15)对结构的屈服状态以及稳定性进行抗震评估。

本方法首先通过结构的刚度和质量分布，得到模态数据，采用与振型叠加法类似的求解方式，对结构进行单一振型的Pushover 分析和多振型叠加的方式求解结构的地震响应。相比振型叠加法采用的振型数量较少，相比于传统的Pushover 方法可以考虑高阶振型的影响，且具有统一的分布荷载模式，结合静力修正方法可以获得较高的计算精度，同时2 阶段Pushover分析得到结构的内力分布，可以对结构的屈服状态和稳定性进行评估。此外，本文理论推导时并未涉及结构类型，因此可运用于多种结构类型的抗震评估中。

2 算例验证

钢管混凝土拱桥Pushover 方法具体运用之前，先对其计算结果的准确性进行验证，由于推导并未涉及到结构类型，因此采用文献[19]单层柱面网壳算例进行验证。由于非线性时程分析方法采用逐步积分的形式，可以考虑结构的几何、材料等非线性行为，是动力分析中相对精确的计算方法，因此参考文献[19]，将本文所提方法与文献[19]的方法、时程方法进行对比验证。

某单层柱面网壳长度为30 m，跨度为15 m，矢高为5 m，其横杆、纵杆、斜杆分别为Φ245×7，Φ140×5，Φ180×6，钢材为Q235，弹性模量为206 GPa，屈服强度235 MPa，切线模量为0.8 GPa，作用重力代表值为1.5 kN/m2的均布荷载并转化为节点质量，具体参数参考文献[19]，如图3 所示，采用有限元软件ANSYS 求解，材料采用双线性随动强化模型模拟。采用Beam189 和Mass21 模拟结构构件和节点集中质量，两纵边为固定铰接约束。

以横向激励为例进行计算，并与文献[19]的模型方法进行对比分析，首先根据式(18)确定振型遴选的阈值为0.018，遴选出动力贡献较大的振型7个，如表1 所示，其中第1 阶振型的动力贡献系数达到了0.688，其余振型相对较小，均在0.01～0.1之间。各振型如图4 所示。选用EI Centro 地震波，主方向经过调幅后达到1.3g，取前10 s 进行计算，采用Rayleigh 阻尼，阻尼比为0.02。以荷载F=λMϕn对结构进行1 阶段Pushover 分析，并按式(6)计算各阶振型的能力曲线，这里仅列出第1阶和第131 阶振型的能力曲线，如图6 所示，其中第1 阶振型的能力曲线与文献[19]吻合。由此，可以得到各阶振型的等效单自由度体系模型。

表1 振型遴选Table 1 Selection table of vibration modes

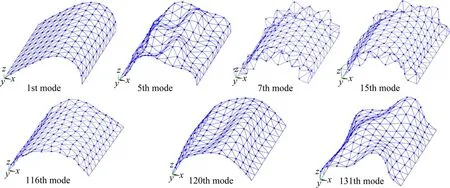
图4 结构振型图Fig.4 Structural modes diagram

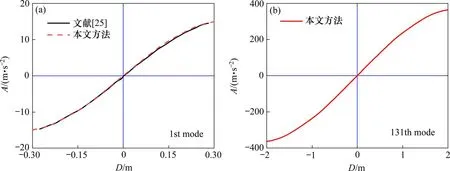
图5 第1和第131阶振型能力曲线Fig.5 Capacity spectrum model for the 1st and 131th order vibrations

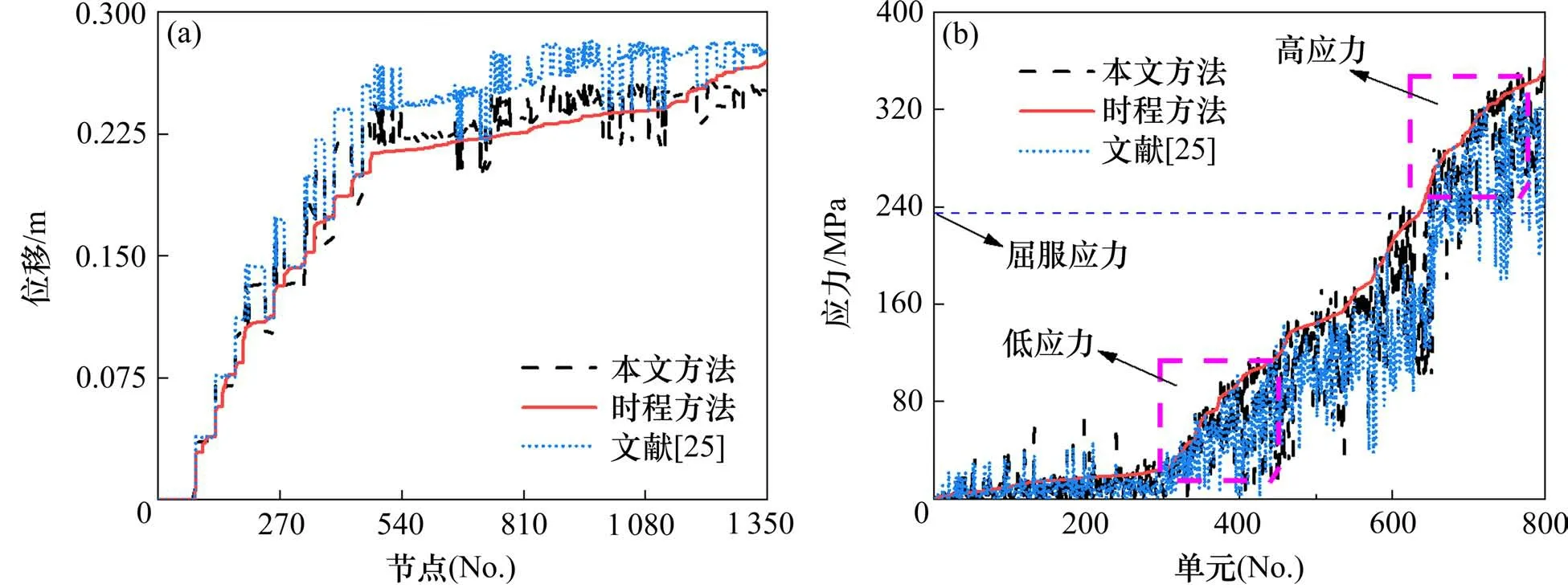
图6 节点位移和单元应力对比图Fig.6 Comparison diagram of node displacement and element stress

根据建立的等效单自由度体系模型，可按式(4)和式(9)计算得到动力解和静力解，再按式(10)计算得到结构的位移，将各节点的位移与时程方法和文献[19]的方法进行对比，如图6 所示。文献[19]的模型由于只考虑第1 阶振型，对于时程分析的位移最大值会被高估，如图6(a)所示，而本文方法保证了动力贡献系数达到90%，使计算的精度提高20%。由F=w2Mu可知，高阶振型的频率较高，其内力贡献相对较大，文献[19]的方法内力结果又会被低估，见图6(b)，而经过静力修正后其内力结果会改善10%，在高应力和低应力区均较时程方法更吻合，其中部分单元进入了屈服阶段。

3 工程实例

3.1 工程概况

广西平南三桥是一座中承式CFST 无铰拱桥，主跨为575 m，计算跨径560 m，矢跨比1/4.0，拱轴系数为1.50，肋宽为4.2 m，桥梁整体布置见图7。弦杆采用Q420qD 钢材，拱肋共分为11 段，上弦杆钢管为Φ1 400×26 mm，下弦钢管厚度变化，第1～4 段为Φ1 400×34 mm，5～7 段采用Φ1 400×30 mm，8～11 段为Φ1 400×26 mm，管内填充C70混凝土。腹杆和横向联系均采用Q345钢材，分别为Φ700×14 mm 钢管、Φ850×18 mm 钢管。吊杆采用37Φ15.2 mm钢绞线，其极限抗拉强度为1 960 MPa。桥面纵梁和吊杆横梁采用Q420钢材。

3.2 计算结果与分析

采用ANSYS 建立空间有限元模型。拱肋弦杆、腹杆、横向联系和桥面纵横梁采用Beam188单元模拟，其中弦杆采用双单元模拟钢管和混凝土；吊杆采用空间杆单元模拟；临时铰接处加强钢板和桥面系使用板单元Shell 63 模拟。吊杆与拱肋、吊杆横梁共节点，拱脚处固定约束，桥面两端采用简支约束。空间有限元模型见图8(a)，模型共有4 437 个节点和11 688 个单元，计算同时考虑几何非线性和材料非线性，其中，核心混凝土本构参考文献[35]，采用多线性随动强化模型模拟，钢管视为理想弹塑性材料，采用双线性随动强化模型模拟。

首先基于有限元模型，进行模态分析，根据式(19)确定阈值δ为0.019，进行计算振型的遴选。以荷载形式F=λMϕn对结构进行1 阶段Pushover 分析，采用ANSYS 的APDL 语言编写相应程序，进行加载求解，提取每一荷载步中各节点的位移以及荷载因子，计算每一荷载步的A和D，绘制A-D曲线，建立各振型的等效单自由度体系模型。根据建立的单自由度体系模型，采用ANSYS 建立单自由度非线性弹簧，弹簧单元采用Combin39，质量单元采用Mass21，进行逐步法求解单自由度动力方程。

选用EI Centro 地震波，经过调幅后达到0.4g，取前10 s进行计算，采用Rayleigh阻尼，阻尼比取0.05，取振型参与系数最大的1 阶、4 阶频率进行计算比例系数，得到α=0.064，β=0.030。得到各等效单自由度体系的动力反应之后，根据本文方法，按式(10)可以得到结构的位移响应。其次，按式(11)进行2 阶段Pushover 分析，获取结构的内力响应，并根据式(12)～(15)建立的钢管混凝土拱的评估指标系数，计算各构件的指标，如图8(b)所示。在0.4g横向地震作用下，吊杆的指标系数在0.125～0.25之间，处于较安全状态；弦杆的强度指标系数均小于0.125，较安全；桥面梁指标系数在0～0.25之间，偏于安全；腹杆的强度和稳定系数有部分达到了1.0，这部分杆件已经进入屈服阶段，且出现失稳，但是桥梁结构整体并没有失稳破坏。

4 结论

1) 提出的钢管混凝土拱桥Pushover 法，能适应具有大量振型的复杂结构，且对本文算例结果位移计算精度整体提高20%，内力结果会改善10%，能对钢管混凝土拱桥进行抗震评估。

2) 提出的基于整体位移的能力谱模型，避免传统方法选取控制节点的困难问题，同时具有明确统一的分布荷载模式，可以提高Pushover 方法对钢管混凝土拱桥的适用性。

3) 所提振型遴选方法，基于振型动力贡献系数确定阈值的大小，降低振型的截断误差，可以将振型数量缩减，提高一定的计算精度。

4) 本文方法通过求解能力谱模型，结合静力修正方法可以获得较高的计算精度，但求解多阶振型时较为繁琐，此外，本文理论推导时并未涉及结构类型，因此可运用于多种结构类型的抗震评估中。