深水采油树生产回路运维可用性分析*

庞 楠，熊中刚，刘 忠，王为庆，徐嘉宏

（桂林航天工业学院机电工程学院，广西桂林 541004）

0 引言

深水采油树作为水下油气生产系统的核心设备，主要用于油气开采、注气注水、修井、流量控制及监测等作业[1]。采油树直接连接油气生产井口，一旦出现故障，会严重影响整套水下生产系统的工作效率。由于深海环境压力高、洋流冲击大、水下能见度差等多项难题，国内有相关水下检测维修经验的公司或院校寥寥无几，检测维修技术还依赖国外，但国外维修售价高、停机期长、人力成本高，大大增加了我国深水油气开发项目的成本和周期，并随时有被国外大厂“卡脖子”的风险，严重威胁了我国能源战略安全和国民经济发展[2-3]。因此，在采油树投入生产前，需要对其进行严格的可靠性设计和预防性维修，并在采油树运维过程中进行实时可靠性状态评估，这对水下油气的安全生产至关重要。

有研究表明[4-5]：深水采油树故障率达到206×10-6，仅次于水下控制系统，失效率是其他核心设备的2.9～18.5 倍。鉴于此，很多学者对采油树关键部件的可靠性开展了相关研究。针对井口连接器方面，Buitrago 等[6]采用传统累积损伤法，根据S-N 曲线定义的局部应力和疲劳抗力计算了井口连接器疲劳寿命。Wang 等[7]在缺乏失效数据情况下，提出了一种将有限元分析与动态贝叶斯模型相结合的疲劳裂纹材料老化故障诊断方法，进行了井口连接器的可靠性分析，得出在出现裂缝的情况下，水下连接器在使用30年后结构失效概率从0.022 8增加到0.207 5；同时，采用蒙特卡罗仿真和基于DBN 的可靠性分析方法，得到在材料强度老化情况下，连接器驱动环结构可靠度达到96.26%的结论[8]；结合赫兹接触理论对油管悬挂器密封性能进行了研究，证明了c 形密封圈在0.1～0.375 mm 干涉范围内具有优良的密封性能和结构完整性[9]。

针对控制系统方面，Liu等[10]提出了一种混合多阶段控制系统规则约束预测方法，解决了采油树控制系统寿命预测过程中不确定性、难以获得实时观测数据以及数据采集噪声影响等问题。岳明阳等[11]基于贝叶斯-GO 法对采油树控制系统进行可靠性分析，得到水下控制模块和生产翼阀失效率最高，失效概率分别达0.023 54 和0.019 543，并建议早期维护须注重对这2个部位进行检测。Liu等[12]提出一种电气控制系统组件的双因素退化模型，建议地面控制系统在连续工作7 000 h 后停机维护，可提高系统可靠性。

另外，Guo 等[13]提出了一种由管理和多个系统代理组成的采油树可靠性建模流程，发现生产节流阀、管线、采油树帽和化学控制阀对系统可靠性影响较大。Hamilton-Smith[14]分析了第三方载荷对采油树框架结构的影响，将关键位置的位移和结果应变值与允许限值进行比较，以确保符合设计要求。Liu等[15]提出了一种基于跳跃连接深度神经网络的非接触故障诊断方法进行阀门泄漏故障诊断，准确率达到98.89%。Cheliyan 和Bhattacharyya[16-17]采用模糊故障树和非支配排序遗传算法进行了采油树可靠性分析。刘超等[18-19]基于历史数据和失效模式分析，应用马尔可夫模型（Markov）、FFTA 及FMEA 对采油树进行可靠性评估，得到采油树可用度为0.999 671；并通过概率重要度分析明确了油管悬挂器化学试剂注入耦合器、节流模块硬管及控制阀是薄弱环节，概率重要度达到了0.999 797。刘健等[20]利用动态模糊子集来描述贝叶斯网络各根节点动态失效概率，很好地解决了因部件故障信息的模糊性与动态性造成的求解精度偏低的问题。

以上针对采油树关键部件进行失效分析的研究达到了较好的可靠性指标评估效果，但目前针对采油树关键部件的可靠性研究多集中在阀门、油管悬挂器、井口连接器、控制模块以及框架结构方面，对采油树生产回路可靠性的分析较少。本文对采油树生产回路进行可靠性和可用性分析，解决生产回路的实时运维评估问题；同时，在现有可靠性研究基础上增加反馈功能，即考虑生产回路维修性数据补充到可靠性评估模型中，达到完善可靠性评估模型变量节点的目的。

1 深水采油树生产回路

本节针对深水采油树生产回路的结构组成、执行功能以及工作原理等方面进行分析，为建立3 条回路的随机Petri网运维模型提供建模基础。

采油树生产回路主要承担深水采油树的油气传输和流量控制的工作。如图1 所示，当系统正常工作时，打开水下控制安全阀，海底油气通过生产回路采集，依次通过生产主阀，生产翼阀和生产节流阀。在阀门周围布置传感器，负责接收温度、压力以及沙粒冲蚀等信号，并传送到水下控制系统进行实时监测。当PTT1数据反馈大于额定值时，水下控制系统发送信号使生产主阀中电液换向阀断电，弹簧复位关闭生产主阀，如果PTT1仍然显示数据，说明生产主阀故障，需要进行修复并保证正常运行，如不能及时维修，则需要关闭生产翼阀，若此时隔离仍不成功，说明生产翼阀故障，则需要继续关闭节流阀和隔离阀。生产节流阀通过阀门打开程度控制生产回路中油气流量，流量计WGFM 统计生产回路实时流量并反馈给水下控制系统。当生产回路的传感器数据反馈小于额定值时，水下控制系统只能接收数据，无法关闭阀门，需要水下机器人操作深水采油树控制面板强行关闭阀门。当生产回路中的阀门无法正常关闭时，深水采油树将进入危险状态。

图1 深水采油树生产回路

2 随机Petri网模型

深水采油树生产回路较为复杂，存在两种或多种失效模式同时发生的情况，为避免可靠性分析过程中的爆炸性问题，本文采用随机Petri 网法进行可靠性分析，首先介绍随机Petri网应用原理和建模流程。

2.1 随机Petri网

随机Petri 网（SPN）系统定义为六元组N=（P，T，F，K，M0，λ），其中（P，T，F）为基网；K为容量函数；M0为初始标识；λ为变迁T转移率的集合，即故障率。故障率与标识状态无关，一般假设元器件随机Petri网中故障率服从指数分布，结构件随机Petri 网中故障率服从威布尔分布。基网定义为三元组N=（P，T，F），P为库所，T为变迁，F为连接弧，满足以下4 点；（1）P∩T= ∅，库所和变迁应没有交集；（2）P∪T≠∅，网中至少要有一个元素；（3）F⊆P×T∪T×P，弧分为两类；（4）dom(F)∪cod(F)=P∪T，网中无孤立元素。其中，dom(F)={x|∃y.(x,y)∈F} ，为定 义 域； cod(F)={x|∃y.(y,x)∈F} ， 为 值 域；P={P1,P2,…,Pn} ， 为 一 个 有 限 的 库 所 集 合；T={t1,t2,…,tq} ，为一个有限的变迁集合；n为库所总数，pi为一个库所，即系统一个局部的状态；P为整个系统的状态；q为变迁总数。在一个Petri 网系统中，可以通过Token 来表示库所的状态，用m（pi）表示库所Pi的Token值，则Token 的分布状态为系统的整体状态，称之为标识，则定义M0=[m（0P1），m（0P2），…，m（0Pn）]为初始标识，代表系统的原始状态。

2.2 生产主阀PMV的随机Petri网模型

针对生产主阀PMV 的运行状态由正常运行到发生泄漏，发生泄漏后确定PMV 失效，然后发现失效，发起命令进行维修，最后通过维修恢复PMV 正常工作状态。该变迁过程如图2 所示，系统初始标识M0=[1，0，0]，此时变迁failure 具有发生权。由于PMV 属于液压元器件，失效和维修分布一般符合指数函数，发现失效后发起开始维修命令符合零延迟狄拉克定律。

2.3 随机Petri网建模流程

在随机Petri 网络中，对系统在不同状态可能发生的事件（故障、测试、维护等）进行建模。过程如下：

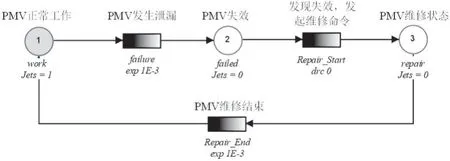
图2 PMV网系统模型

（1）首先列出系统所有库所和变迁：明确深水采油树生产回路不同状态以及不同状态之间的转换过程；

（2）确定库所和变迁逻辑关系：明确每个变迁的输入和输出；

（3）确定所有变迁发生分布函数：一般阀门、传感器、流量计等电控、液压元器件的失效模式一般服从指数分布；机械结构的失效模式一般服从威布尔分布；

（4）建立系统随机Petri 网模型：根据库所、变迁以及库所和变迁的逻辑关系建立深水采油树生产回路的随机Petri网模型；

（5）完成可靠性及可用性等分析：基于系统随机Petri 网模型和变迁发生分布函数关系，完成深水采油树生产回路的可靠性和可用性指标求解。

3 深水采油树生产回路可靠性分析

建立Petri 网模型之前，根据系统实际工作情况和可靠性基础知识作如下假设：

图3 生产回路Petri网模型

（1）系统中所有部件和元器件的技术参数都满足设计要求，且从完美状态开始工作；

（2）阀门、传感器、流量计等电控、液压元器件失效率的失效模式均服从指数分布；机械结构部件失效率的失效模式均服从威布尔分布；

（3）各失效模式均互不影响，相互独立；

（4）忽略控制系统的失效。

基于第2节深水采油树生产回路分析，建立如图3所示的深水采油树生产回路的随机Petri网模型。

该模型中包括11个库所：

（1）库所1：work，生产回路运行正常状态；

（2）库所2：failure，PMV故障状态；

（3）库所3：repair，PMV维修状态；

（4）库所4：failure，PWV故障状态；

（5）库所5：repair，PWV维修状态；

（6）库所6：failure，PCV故障状态；

（7）库所7：repair，PCV维修状态；

（8）库所8：failure，PIV故障状态；

（9）库所9：repair，PIV维修状态；

（10）库所10：failure，生产回路故障状态；

（11）库所11：repair，生产回路维修状态。

模型的23 个变迁如表1 所示（失效和维修率数据来源于OREDA海洋工程可靠性手册）。

该模型可以用来模拟深水采油树生产回路实际运行流程：

（1）库所1 最初包含一个token，因此进行失效转换是初始状态唯一有效的转换；

（2）当生产回路发生任一失效时，按照失效模式发生的分布函数进行变迁。此时，生产回路运行正常状态的token将被设置为0，失效模式所在库所token数为1；

（3）当失效模式发生时，会分为是否进行维修两种状态，且两种状态触发变迁不同，如当PMV 发生泄漏，分为发现泄漏失效和没有发现失效两种情况，如果发现泄漏失效，则Repair_Start 变迁传递为true，PMV 进入维修状态；如果没有发现泄漏失效，则没有发现PMV 失效的变迁传递为true，PMV 长期处于泄漏状态，会导致生产回路失效；

表1 随机Petri网模型的23个变迁信息

（4）一旦修复开始（Repair_Start 变迁传递为true），水下控制系统会立刻发出指令，关闭相应元器件并进行维修，因此修复将立即开始，设置修复变迁的延迟定律为零延迟狄拉克定律，token直接转移到维修状态的库所；

（5）token 到达正常工作状态的库所按照Repair_End变迁的分布函数进行；

（6）启动Repair_End 变迁后将从Repair 状态删除token，将一个token 放入Work 位置。因此生产回路回到正常工作状态。

4 生产回路可靠性仿真、结果分析及验证

4.1 可靠性仿真

在仿真模式下，当Petri 网模型中变迁有效时，变迁可以随设定的分布函数进行触发，也可以自动触发，自动触发零延迟（参数为0 的狄拉克定律）的变迁。在几个狄拉克变迁“冲突”的情况下，这些变迁的发生是根据它们的优先级进行的，按照时间顺序进行。本节对生产回路进行可靠性仿真分析。

根据生产回路随机Petri 网模型可知，N=（P，T，F，K，M0，λ），其中P={p1，p2，p3，p4，p5，p6，p7，p8，p9，p10，p11}；T={t1，t2，t3，t4，t5，t6，t7，t8，t9，t10，t11，t12，t13，t14，t15，t16，t17，t18，t19，t20，t21，t22，t23}；F={（p1，t1），（p1，t2），（t1，p2），（t2，p2），（p2，t3），（p2，t4），（t3，p10），（t4，p3），（p3，t5），（t5，p1），（p1，t6），（p1，t7），（p1，t8），（t6，p4），（t7，p4），（t8，p4），（p4，t9），（p4，t10），（t9，p10），（t10，p5），（p5，t11），（t11，p1），（p1，t12），（p1，t13），（p1，t14），（t12，p6），（t13，p6），（t14，p6），（p6，t15），（p6，t16），（t15，p10），（t16，p7），（p7，t17），（t17，p1），（p1，t18），（t18，p8），（p8，t19），（p8，t20），（t19，p10），（t20，p9），（p9，t21），（t21，p1），（p10，t22），（t22，p11），（p11，t23），（t23，p1）}；M0={m0（p1）=1，m0（p2）=m0（p3）=m0（p4）=m0（p5）=m0（p6）=m0（p7）=m0（p8）=m0（p9）=m0（p10）=m0（p11）=0}，因此初始状态变迁t1、t2、t6、t7、t8、t12、t13、t14以及t18具有发生权。

4.2 可靠性结果分析及验证

图4 所示为深水采油树生产回路失效率对平均无故障时间的影响。系统MTTF 随失效率的增加而减小，根据OREDA 数据库推荐的失效率进行计算，生产回路平均无故障时间为9 998.2 h。系统的可用度可以表示为系统平均无故障时间与平均无故障时间和平均维修时间加和的比值，根据生产回路随机Petri 网模型可求得系统的平均维修时间，如表2所示。

图4 生产回路失效率对平均无故障时间的影响

表2 生产回路不同失效率的平均维修时间

由OREDA数据库可知，当失效率量级达到10-6～10-4时，系统平均维修时间在0.3～456.0 h内，本文得出1.84、7.57、131.07 h 均符合系统平均维修时间取值范围。图5所示为深水采油树生产回路失效率对生产回路可用度的影响。由图可知，系统可用度随失效率增加而减小，当失效率低于10-3时，生产回路的可用度下降趋势比较平缓，当失效率大于10-3时，可用度随故障率的增加而迅速下降。根据OREDA 数据库推荐的失效率计算，生产回路可用度为0.999 8。

图5 深水采油树生产回路失效率对系统可用度的影响

5 结束语

本文针对深水采油树生产回路进行可靠性分析，提出了基于随机Petri 网的运维可靠性分析方法，避免了可靠性分析过程中的爆炸性问题，得到主要结论如下：

（1）考虑系统维修性的影响，对深水采油树生产回路进行可靠性分析，得到了平均无故障时间及可用性曲线；

（2）通过随机Petri 网可靠性模型分析，得到了采油树生产回路不同失效率情况下系统的平均维修时间，如针对生产回路，当失效率分别为10-6、10-5、10-4、10-3、10-2和10-1时，系统平均 维修时间 分 别为1.84、7.57、131.07、796.6、4 732.77、9 014.98 h，以上结果通过了OREDA数据库的数据验证；

（3）通过随机Petri 网可靠性模型分析，得到了不同失效率情况下，采油树生产回路的可靠度；同时基于OREDA 数据库统计的失效率进行计算，得到深水采油树生产回路的平均无故障时间约为9 998.2 h。