TC4钛合金材料钻削仿真与参数优化

贾宗强,白海清,2,张鑫何,张 乐,李高伟

(1.陕西理工大学 机械工程学院, 陕西 汉中 723001;2.陕西省工业自动化重点实验室, 陕西 汉中 723001)

0 引言

TC4钛合金因耐热性好、比强度高、耐高温、耐腐蚀,具有良好的综合性能[1]。但TC4钛合金材料导热系数低、化学性质活泼、弹性模量小,切削加工过程温升较高且容易出现“让刀”、回弹和切削振动现象,是典型的难加工材料[2]。尤其在钻削加工时,散热条件差[3],使钻削温度更易升高,导致刀具的材料硬度降低、磨损增加、寿命减少,影响加工效率和表面质量可加工性能较差。通过对钻削加工参数的优化,降低轴向力和切削温度可以改善加工表面质量、减少刀具磨损[4],对提高钛合金材料钻削加工性能的研究具有重要意义。

利用有限元仿真技术,可得到传统钻削实验中难以测得的钻削力和钻削温度等参数,降低试验研究成本。目前,国内外学者为了提高钛合金材料的可钻削加工性,结合计算机仿真,做了大量的研究。谈志晶等[5]通过仿真与实验对比,证明了用有限元仿真模型来预测钛合金钻削力、钻削温度的可行性。房晨等[6],利用有限元仿真研究了硬质合金麻花钻的不同外缘后角、螺旋角和横刃斜角等对钛合金钻削性能的影响,发现相比于其他刀尖几何参数,横刃斜角和螺旋角分别对轴向力及切削温度影响更为显著。田卫军等[7]研究了钻削参数对轴向力和温度的影响,发现相比于转速来说,钻削力对进给量的变化最为敏感。冯杰等[8]利用ABAQUS有限元分析软件对TC4钛合金薄壁件进行加工仿真,建立了钻削轴向力随转速、进给量变化的响应曲面,研究表明,进给量对钻削力的影响最为显著,随着进给量的增大,轴向力不断增大。刘成炜等[9]利用ABAQUS建立了钻削过程冷却换热仿真模型,研究了不同冷却方式对钛合金薄壁件钻削温度场的影响。姜铭等[10]基于有限元仿真分析结果,研究了钻头刃形和几何参数对钛合金薄壁件钻削力的影响,发现随着螺旋角的增大,轴向力先降低后升高。可见,以上文献大多只研究了钻削参数对钻削力、钻削温度等,反映了钻削性能评价指标的影响规律,在对评价指标预测模型的建立和钻削参数优化方面的研究还有所欠缺。胡立湘等[11]通过实验得到了钻削用量对轴向力、表面粗糙度和切屑形态的影响规律,并拟合数据得到了钻削力的指数预测模型,但最后只是给出了参数优选原则。张文盟[12]研究了不同的麻花钻几何参数对钻削力、扭矩和孔壁残余应力的影响规律,并分别将以上三者作为优化目标得到了刀具的最佳几何参数组合。但是,对单一目标的优化通常难以满足工程实际的需要。刘士荃等[13]采用熵值法确定了优化目标的权重,对多个优化目标的回归模型进行加权组合得到一个评价函数,最后通过单目标遗传算法实现了钻削参数的优化。这种方法相比于普通的多目标优化方法,其解的含义和分布情况不够直观。王永鑫等[14]基于响应面实验,建立了转速、进给速度和步进量对轴向力的数学预测模型,最后得到了使表面质量较优和加工效率更高的最优参数组合,尽管其实现了钻削工艺参数的多目标优化,但忽略了不同评价指标之间的相对重要性(即权重)。对评价指标权重的忽视,将降低多目标优化结果的可信度。且其结果作为一个解集,难以满足生产实际的需要,具体解的选取方法尚缺少理论依据。

建立在各钻削加工参数对评价指标影响规律分析的基础上,对钻削参数进行多目标优化,是提高TC4钛合金钻削加工性能的重要途径,其中对评价指标权重的研究又是提高优化结果可信度的关键。将刀具几何参数中对钻削力和钻削温度影响较为显著的横刃斜角、螺旋角以及在切削用量中影响较为显著的进给量作为影响因素,设计响应面试验方案,利用金属切削有限元仿真软件AdvantEdgeFEM对麻花钻钻削TC4材料的过程进行仿真,并通过实验验证了其结果的可靠性。通过仿真结果得到了评价指标的影响规律,并建立了钻削力和钻削温度的预测模型,将其作为多目标遗传算法的目标函数,得到了多目标优化结果的非劣解集,最后通过熵权法分别考虑了钻削力和钻削温度的权重,并利用TOPSIS综合评价法实现了对非劣解集的二次筛选,得到了唯一解。为提高多目标优化结果的可靠性,使多目标优化方法更好地适用于生产实际等方面提供了一定的参考和依据。

1 建立钻削模型

AdvantEdge软件是基于材料特性的金属切削有限元分析软件,有着强大的切削模拟功能,可以较好地模拟硬质合金刀具对钛合金材料的切削仿真[15-16]。利用AdvantEdge软件进行麻花钻对钛合金材料的钻削过程仿真,工件材料为Ti6Al4V、刀具材料为硬质合金、工件尺寸为12 mm×12 mm×3 mm、麻花钻直径为6 mm、转速为2 123 r/min(换算成切削速度为40 m/min)、顶角为135°,工作环境温度选择20 ℃(精密机床工作一般要求车间温度在20 ℃左右[17])。此处,Ti6Al4V钛合金材料的本构为Johnson-Cook本构模型[18-19],即:

(1)

表1 Ti6Al4V钛合金材料参数

在AdvantEdge软件中使用自动网格划分功能对工件和麻花钻模型进行网格划分,并且可以实现在切削刃处的网格加密,划分后的有限元网格模型如图1所示。

图1 钻削加工的有限元模型

设置好工件形状尺寸、工件材料、刀具材料和麻花钻的钻削参数,并划分好网格后,即可进行钻削过程的有限元仿真模拟。

2 模拟与分析

2.1 单因素有限元模拟

为了探究各因素对评价指标的影响,首先设计了单因素数值模拟方案,如表2所示。以分析钻削过程中的轴向力和切削温度随进给量、螺旋角和横刃斜角的变化规律及显著性,为后面响应面分析做准备。

表2 单因素模拟方案

本文中对横刃斜角的表述,参考了软件自身设置习惯和相关教材,为了避免产生歧义,于是特意在此做出表述,横刃斜角如图2所示。

图2 麻花钻横刃斜角

2.2 结果与分析

按单因素模拟方案表,在有限元分析软件中做切削仿真模拟,将轴向力、切削温度随单因素变化的结果数据统计并导入Origin软件中绘制变化曲线。

2.2.1进给量对轴向力和温度的影响

控制螺旋角为28°、横刃斜角为120°不变,分别取进给量为0.06、0.10、0.14、0.18 mm/r时轴向力和切削温度如图3所示。由图3可知,进给量对轴向力和切削温度的影响是显著的,随着进给量的增加,轴向力呈近似线性递增变化,切削温度与轴向力的变化规律近似。进给量过小,会导致加工效率低,进给量过大,则轴向力和切削温度太高,于是选择进给量的取值范围为0.1～0.14 mm/r,用于响应面设计。

图3 轴向力和温度随进给量的变化趋势

2.2.2螺旋角对轴向力和温度的影响

控制进给量为0.12 mm/r、横刃斜角为120°不变,分别取螺旋角为25°、28°、31°、34°时轴向力和切削温度如图4所示。

图4 轴向力和温度随螺旋角的变化趋势

由图4可见,螺旋角的影响是显著的,随着螺旋角的增加,轴向力和切削温度先减小后增加。螺旋角在区间[25°, 28°]内轴向力和切削温度随着螺旋角的增加而降低,这是因为增大螺旋角有利于排屑,并且螺旋角越大前角越大,可以减小钻头的摩擦;在区间[28°, 31°]内轴向力随切削温度的增加而降低,这是因为温度升高导致材料软化引起的;在区间[31°, 34°]内轴向力和切削温度随螺旋角的增大而增大,这是因为螺旋角过大会削弱切削刃的强度、刚度和散热条件[20]。当螺旋角为28°时切削温度最小,当螺旋角为31°时轴向力最小,于是选择螺旋角为28°～34°用于响应面设计的因素水平。

2.2.3横刃斜角对轴向力和温度的影响

控制进给量为0.12 mm/r,螺旋角为28°不变,分别取横刃斜角为120°、125°、130°、135°时轴向力和切削温度的变化如图5所示。由图5可知,随着横刃斜角的增大轴向力和切削温度增大,综合考虑轴向力和切削温度后,选择横刃斜角为120°～130°的范围内进行取值。

图5 轴向力和温度随横刃斜角的变化趋势

2.2.4实验验证

为了验证仿真结果的准确性,以2.2.1节的单因素仿真为例,进行钻削加工实验。如图6所示,刀具采用定制的整体硬质合金麻花钻(直径6 mm、顶角135°、螺旋角28°横刃斜角120°),其合金类型为YG6X。工件材料为TC4钛合金(厚度10 mm),钻孔深度为5 mm。在DMU50数控加工中心上进行钻削实验,并用瑞士KISTLER公司生产的9 257 B压电式测力仪系统配合DEWESoftX3数据采集软件采集钻削轴向力。

图6 实验装置

通过KISTLER测力仪得到加工过程中微弱的压电信号,经过电荷放大器放大得到模拟信号,再经过A/D转换器将模拟信号转换为数值信号导入数据处理系统,得到钻削轴向力在时间历程上的变化情况如图7所示。

图7 不同进给速度下的轴向钻削力实验值

图7中分别为0.06、0.1、0.14、0.18 mm/r进给速度的单因素实验条件下轴向力的实时变化曲线图,可见随着钻尖钻入,钻削轴向力逐渐增大,当钻尖完全钻入则轴向力进入稳定阶段,由于材料未钻透在抬刀的瞬间轴向力随即消失。取稳定钻削阶段轴向力的平均值作为该组实验值,并将仿真值与实验值作对比,结果如表3所示。

表3 仿真与实验结果对比

可以发现仿真值与实验值较为接近,误差都在15%以内,也即仿真结果可信度在85%以上,说明后续的仿真结果具有一定的实际意义。

2.3 响应面模拟方案

2.3.1确定因素水平

根据上文所做的单因素分析结果,进一步设计了响应面模拟方案。采用Box-Behnken Design(简称 BBD)响应曲面设计方法,综合考虑进给量、螺旋角、横刃斜角对钻削过程中轴向力和切削温度的影响,其因素水平设计如表4所示。

表4 因素水平表

2.3.2模拟方案与结果

依据表4所列因素水平,在Design-Expert软件中按照BBD方法设计响应面方案,在金属切削有限元分析软件中进行仿真。模拟方案及结果如表5所示。

表5 响应面方案设计及结果

2.4 方差分析

2.4.1轴向力方差分析

根据模拟结果,在Design-Expert软件中得到轴向力的二次多项式回归模型如下:

FZ=70.156+9839.7f+136.835ω-46.675ψ-

111.188fω-57.757fψ+0.036ωψ+

25357.5f2-1.907ω2+0.234ψ2

(2)

钻削轴向力回归模型的方差分析结果如表6所示。

表6 轴向力二次模型方差分析

为了进一步检验模型的准确性,判断模型是否存在过拟合的问题,有必要引入误差分析和残差分析,分别如图8和图9所示。

图8 轴向力回归模型的标准化残差及拟合误差图

图9 切削温度回归模型标准化残差及拟合误差图

2.4.2切削温度方差分析

切削温度的二次多项式回归模型如下:

T=9 360.09+13 951.71f-189.03ω-110.86ψ+

58fω-66.775fψ+0.185 8ωψ-26 172.5f2+

2.517 8ω2+0.453 7ψ2

(3)

切削温度回归模型的方差分析结果如表7所示。

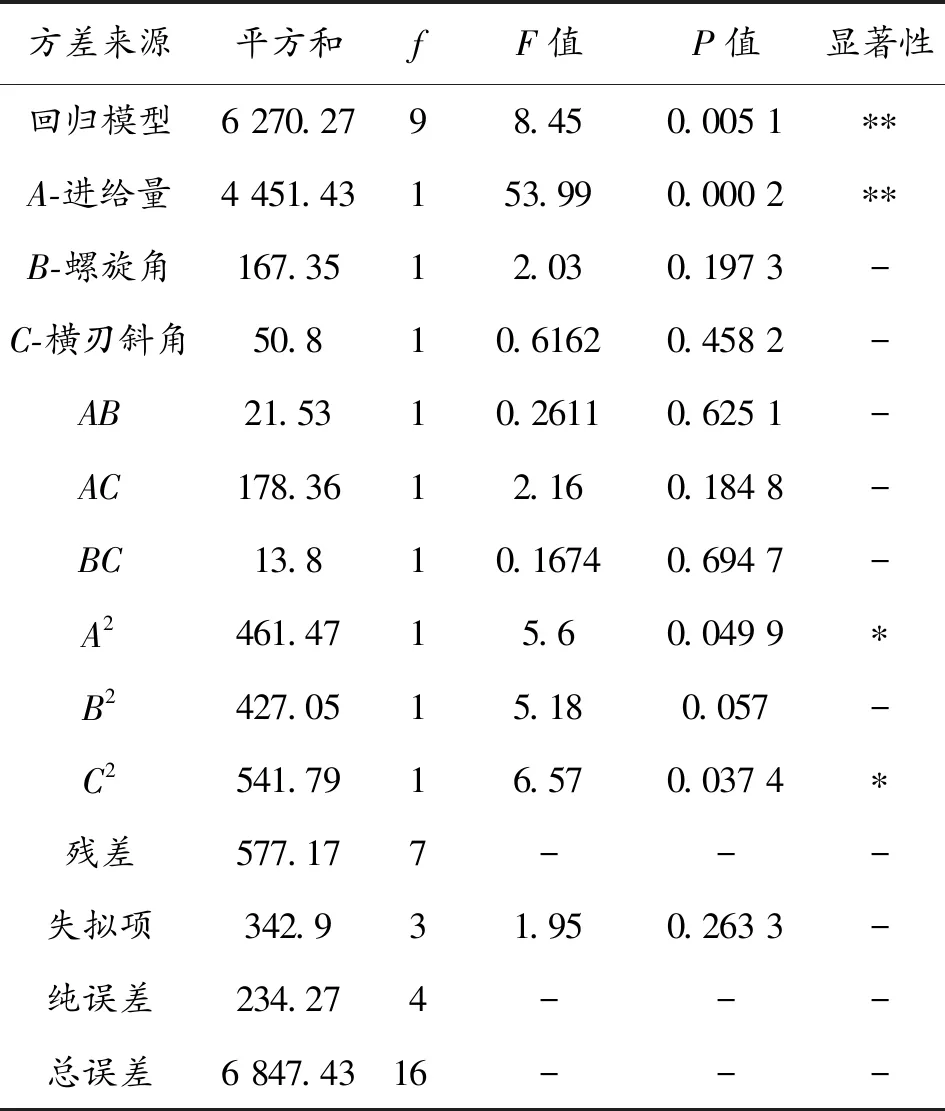
表7 切削温度二次模型方差分析

从图8和图9可见,残差基本分布在一条直线上,并且主要集中于直线的中间位置,说明模型的残差分布符合正态分布规律,拟合误差都控制在了±3%以内;如表8所示,R2均大于0.9、调整后的R2均大于0.8(越接近于1则回归方程越准确),说明2个回归模型拟合精度高、预测结果可靠、置信度高[21]。

表8 回归模型符合度统计

2.5 响应面分析

2.5.1轴向力响应面分析

图10为不同钻削参数组合下的轴向力响应面,可以发现进给量、螺旋角和横刃斜角三者之间的交互作用对轴向力的影响很大。图10(a)为进给量和螺旋角对轴向力的响应图,可以发现,相比于螺旋角,进给量对轴向力的影响更大;图10(b)为进给量和横刃斜角对轴向力的响应图,可以发现,相比于横刃斜角,进给量对轴向力的影响更大;图10(c)为螺旋角和横刃斜角对轴向力的响应面图,可以发现,相比于螺旋角,横刃斜角对轴向力的影响更大。综上所述,各钻削参数对轴向力影响的主次顺序为:进给量>横刃斜角>螺旋角。综合图10(a)、图10(b)、图10(c)可以发现,轴向力随各参数的增大而近似线性增大,因此,为使钻削加工的轴向力更小,应选择较小的进给量、螺旋角和横刃斜角。

2.5.2切削温度响应面分析

图11为不同钻削参数组合下的切削温度响应面,可以发现,各参数之间存在不同程度的交互作用。图11(a)为进给量和螺旋角对切削温度的响应图,可以发现相比于螺旋角,进给量对切削温度的影响更明显;图11(b)为进给量和横刃斜角对切削温度的响应图,可以发现,相比于横刃斜角,进给量对切削温度的影响更大;图11(c)为螺旋角和横刃斜角对切削温度的响应面图,可以发现螺旋角和横刃斜角对切削温度的影响均不显著。各钻削参数对切削温度影响的主次顺序为:进给量>螺旋角>横刃斜角。响应面分析结果与方差分析结果一致。从图11还可以发现,切削温度随进给量的增加而升高,且变化速率逐渐减小,这是因为增加进给量使材料去除率提高,切屑带走了更多的热量所致;切削温度随螺旋角和横刃斜角的增加呈先减小后增大的变化规律,所以说螺旋角和横刃斜角的取值应接近中间水平。

图11 不同钻削参数组合下的切削温度响应面

3 多目标优化

3.1 多目标优化模型

遗传算法具有较强的全局寻优能力,是一种先进的智能仿生优化方法。以轴向力和切削温度的二次回归模型为目标函数进行多目标优化。多目标优化问题可以描述为

min[f1(x),f2(x),…,fm(x)]

(4)

(5)

式(4)、式(5)中:fi(x)为目标函数;x为待优化的变量;ub和lb分别为变量的上下限;Aeq*x=beq为线性等式约束;Aeq*x≤beq为线性不等式约束。在多目标优化中,一个目标函数的优化往往会以另一个目标函数的劣化为代价,于是,通过多目标遗传算法优化得到的最优解,称为非劣解集,又称为帕累托最优解。

3.2 多目标遗传算法参数设置及优化结果

3.2.1参数设置

设置遗传算法进化代数为2 000代,终止条件阈值为1×10-4,初始种群规模为200,帕累托前端系数为0.3,其他保持默认设置,其中约束条件为:

(6)

3.2.2多目标优化结果

调用gamultiobj函数进行迭代寻优,达到终止条件阈值后得到帕累托最优解如图12所示。

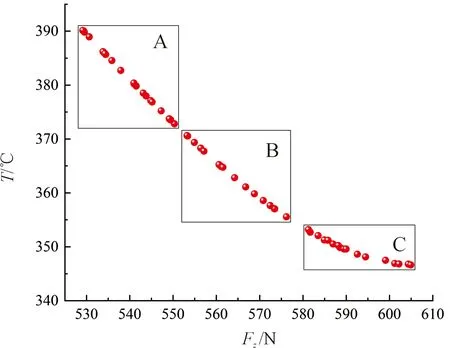
图12 轴向力和切削温度优化的帕累托前沿

由图12可见,随着切削温度的降低,轴向力逐渐升高。在区域A中,随着轴向力的降低切削温度急剧升高;在区域C中,随着切削温度的降低轴向力急剧增大;而在区域B中各评价指标的变化不大,轴向力和切削温度均保持在期望的范围内。于是选择区域B的第30～46个非劣解如表9所示[22]。

表9 区域B的非劣解集

3.3 多目标优化结果的二次筛选

然而区域B中的非劣解数目仍旧太多,难以满足工程实际的需要,要求决策者根据实际情况从中进行选择,但所选结果对决策者自身专业水平的依赖性较大。事实上,在生产实际当中,由于各评价指标自身的特点不同,各非劣解的相对优度也不完全相同,这里可以通过综合评价方法做进一步筛选解决此问题[23]。综合评价方法有很多种,如层次分析法、主效应分析法、TOPSIS法、灰色关联度分析法、模糊分析法等,其中TOPSIS法能充分利用原始数据的信息,反映各方案之间的真实差距,结合熵权法以考虑权重的影响,可以进一步提高其评价结果的准确性和可靠性。本文选择熵权-TOPSIS法对非劣解集进行评价,其工作流程如图13所示。

熵权-TOPSIS法的具体实现过程如下:

Ⅰ.熵权法计算权重

步骤1数据标准化

(7)

得到标准化矩阵Y={yij}m×n, 其中,m、n分别为评价对象和评价指标的数量。

步骤2计算比重矩阵

(8)

式(8)中,pij表示第j个评价指标下第i个评价对象的样本值占该指标的比重,并作为计算信息熵时的概率。

步骤3计算各指标信息熵值

(9)

式(9)中,-lnpij=Iij为第j个评价指标下第i个评价对象的信息量,随着比重的增大而减小。

步骤4计算各评价指标权重

(10)

式(10)中,1-ej=dj表示第j个评价指标的信息效用值,信息熵越大则信息效用值越小。

Ⅱ.TOPSIS法综合评价

假设共有i个评价对象、j个评价指标,则数据原始矩阵如下:

(11)

(12)

步骤1评价指标正向化

由于评价指标的类型有很多,因此优化的方向也是不同的,需要对各指标进行正向化处理使之统一成为高优指标,方法如下:

(13)

步骤2构造归一化初始矩阵

为了消除各评价指标之间因量纲的不同所导致的误差,对原始数据做归一化处理,处理方法是将每一列各元素都除以当前列向量的2-范数,如下:

(14)

原始数据经过归一化处理后得到了下面这个矩阵,我们称之为归一化矩阵,即:

(15)

步骤3确定正理想解和负理想解

基于归一化矩阵Z,采用余弦法找出正理想解和负理想解。正理想解是由每列元素的最大值构成的1×j维矩阵,负理想解是由每列元素的最小值构成的1×j维矩阵,有:

max{z1j,z2j,…,zij}]

(16)

min{z1j,z2j,…,zij}]

(17)

步骤4计算每一个评价对象与正理想解和负理想解的距离

(18)

步骤5计算每个评价对象与正理想解的接近程度

(19)

其中0≤Ci≤1,越接近于1,则评价对象与理想解贴近度越高,说明评价对象越优。熵权-TOPSIS法对所选非劣解集的评价结果如图14所示。可以发现,贴进程度最高的3个最优解依次为非劣解40(优度最高)、非劣解43、非劣解38,所对应的最优钻削加工参数值如表10所示。

图14 区域B非劣解集综合评价结果对比

表10 所选非劣解及对应的加工参数值

此处,结合表1可以发现,通过多目标智能优化算法所得到的最优钻削参数组合与响应面分析所得结果相符合。

3.4 优化预测结果验证

最后,为了检验优化预测结果的可靠性,将表10中的参数在有限元软件中进行仿真,做了对比验证[15],其结果如表11所示。

表11 预测结果对比

各评价指标的误差均在7%以内,说明了回归模型有较好的预测精度,优化结果预测准确度较为可靠。

4 结论

1) 进给量、螺旋角和横刃斜角,相互之间的交互作用对钻削轴向力和钻削温度的影响不显著。各参数对轴向力影响的主次顺序为:进给量>横刃斜角>螺旋角;对钻削温度影响的主次顺序为:进给量>螺旋角>横刃斜角。

2) 二次响应曲面回归模型可以较好地预测实验结果,结合多目标遗传算法可以很好的实现对麻花钻切削参数的多目标全局性优化,模型的拟合优度均在0.9以上、预测误差都小于7%,模型精度较高,优化结果准确可靠。

3) 利用熵权-TOPSIS综合评价方法对多目标优化所得非劣解集进行二次筛选,得到了唯一解、提高了所选最优解的可靠性和可信度,满足了生产实际的需要。当进给量为0.10 mm/r、螺旋角为31.43°、横刃斜角为121.68°时,TC4钛合金材料的钻削加工性能达到最优。