壁温对类HTV-2飞行器气动力计算的影响

陶善聪,周 毅,时晓天

(1.中国航天空气动力技术研究院, 北京 100074;2.南京理工大学 能源与动力工程学院, 南京 210094)

0 引言

高超声速飞行器速度高、机动快、突防强,在航空航天、军事等领域表现出色,成为世界各国研究的重点[1]。而气动力特性影响着高超声速飞行器总体方案和飞行性能,因此准确预测高超声速飞行器气动力特性意义显著。风洞试验是预测高超声速飞行器气动力特性的重要手段,但受风洞设备和测试技术的限制,高超声速风洞试验无法完全复现飞行状态下的流场环境[2],地面预测气动力与高空真实环境飞行气动力存在差异。数值模拟手段能够完全模拟真实飞行环境,且相比于风洞试验无洞壁支撑等干扰,成为预测高超声速飞行器气动力特性的主流手段之一[3-5]。

在实际工程计算中,无论是数值模拟风洞试验状态还是模拟高空飞行状态,需要指定壁面的温度条件,其数值大小依赖于计算经验给定,若偏离正常值很可能得到误差非常大的气动力预测结果。因此需要进一步评估壁温对高超声速气动力计算和高超声速流场流动特性的影响。刘杰等[6]研究了壁温对高超声速飞行器阻力的影响,提出了预测高超声速飞行器阻力时,要同时预测马赫数、雷诺数、壁温与来流静温比3个相似参数。范月华等[7]采用国家数值风洞工程提供的NNW-Flowstar软件数值评估了壁温对高马赫数层流摩阻计算的影响,指出应当根据壁面不同部位气动加热的程度,发展可实现所有位置壁温的高效自适应调整技术。王刚等[2]应用理论分析方法证实了黏性干扰参数是高马赫数高超声速气动力实验中的主要模拟参数,并且说明了壁温条件对黏性干扰效应具有显著影响。王振清等[8]分析了壁面温度对来流脉冲扰动下高超声速流动的影响主要集中在边界层,壁温不同表面密度和摩擦因数分布差异明显。贺元元等[9]利用脉动燃烧风洞、常规高超声速风洞和数值计算3种手段评估了壁温比对模型气动性能的影响,指出了壁面对边界层速度型的传热是差异主要诱因。窦立谦等[10]采用参考温度法建立高超声速飞行器气动黏性模型,分析了黏性阻力及飞行器弹性形变随壁面温度变化的规律,结果表明随壁面温度升高,黏性阻力升高。Zhong等[11]利用化学非平衡方法研究了壁温对火星进入舱气动性能的影响,指出壁温对进入舱前体气动特性影响较小,对后体气动性能影响显著。Xu等[12]采用直接数值模拟方法研究了壁温对高超声速边界层可压缩效应的影响,说明了流向脉动、法向脉动的正负分布导致了冷壁增强近壁流场的可压缩效应。

总的来说,国内外学者已经在壁温对高超声速气动特性的影响进行了相当的研究,研究重点主要是壁温对高超声速飞行器气动阻力的影响,并且将影响原因归结为来流温度与壁面温度之比的不同,但是未对壁温比导致边界层内流动特性的变化展开深入的探讨,而边界层内流动特性又是影响高超声速飞行器气动特性的决定因素。鉴于此,本研究中从数值模拟风洞试验状态及高空飞行状态2个方向剖析壁温对类HTV-2外形飞行器高超声速气动力计算的影响,以期获得能够指导利于工程数值计算的规律性结论。

1 数值方法及模型网格拓扑

1.1 数值方法

控制方程为无量纲形式三维不可压Navier-Stokes方程:

(1)

式(1)中:t为时间;Q为守恒变量;x、y和z为直角坐标系坐标;Ec、Fc和Gc分别为x、y、z方向的对流通量;Ev、Fv和Gv分别为x、y、z方向的黏性通量;Reref为特征雷诺数。采用有限体积法求解上述控制方程,对于空间离散利用二阶迎风格式计算对流通量,应用Minmod TVD(total variation diminishing)限制器抑制激波附近的非物理振荡,瞬态项采用隐式求解并且通过多重网格方法加速迭代收敛。湍流模型采用Realizablek-ε湍流模型,该模型对强逆压梯度的边界层流动、流动分离和二次流表现较好。

1.2 模型及网格

HTV-2是美国空军在“猎鹰”计划下重点发展的高超声速技术飞行器,其构想是发展一种在临近空间长时间滑翔飞行、机动作战的无动力新型武器装备,并且进行了2次飞行试验验证技术方案,但均已失败告终,从失败结果上启示须高度重视空气动力学在高超声速飞行器研制中的作用和地位[13]。

因此,本研究中选用模型为典型高超声速飞行器类HTV-2,坐标系以头部为原点,沿轴线指向尾端为x轴正方向,y轴在飞行器纵向对称剖面上,向上为正,z轴按右手系规定。类HTV-2外形(见图 1)同风洞试验外形及尺寸相同[14-15],流向轴长L为0.427 m,底部面积为0.010 65 m2。计算网格采用结构六面体半模网格(见图 2),网格拓扑保持良好的正交性,第一层网格高度为1×10-5m,壁面y+<1。

2 壁温对风洞试验状态计算的影响

通过与风洞试验结果对比分析可验证数值方法的正确性,并且考察试验工况下壁温对高超声速气动力计算的影响。试验在中国航天空气动力技术研究院的FD-07风洞中进行[14-15],试验马赫数为6,前室总压为2 MPa,具体参数见表 1(其中Ma为马赫数,P0为总压,P∞为静压,q∞为动压,T0为总温,Re为单位雷诺数)。试验所用天平为TG624C六分量天平,通过静校,天平的最大标准不确定度为0.5%。数值计算来流条件与试验相同,壁面采用等温壁(Tw=300 L)和绝热壁((∂q/∂n)w=0)2种处理方式。为验证网格无关性,计算了3套网格(总网格量分别为200万、470万和820万)作为比较,并且提供了层流的计算结果。

表1 风洞试验来流参数

图3给出了数值计算与风洞试验气动力结果的对比示意图。

其中图3(a)为轴向力系数Cx示意图,图3(b)为法向力系数Cy示意图,图3(c)为俯仰力矩系数Cmz示意图(参考点为头部顶点)。由图3可知,不同网格量之间轴向力系数Cx最大误差不超过5%,法向力系数Cy和俯仰力矩系数Cmy最大误差不超过0.2%,表明网格对计算结果无影响,因此以下结果分析均采用200万网格计算结果。不同壁面处理方式的数值计算结果相差细微,并且与风洞试验结果十分符合,表明数值计算结果的正确性。

图4和图5分别给出了等温壁和绝热壁条件下在0°攻角不同流向位置压力分布。从其中可以看出,随着流动沿流向发展,侧缘压力逐渐减小,2类壁温条件对压力分布影响不大。为了分析壁温对边界层的内在影响,提取图4和图5中粗实线代表的中心对称面和壁面不同流向位置参数特性如图6所示。

高超声速气动力由压力部分和黏性部分组成

F=Fp+Fv

(2)

因此对比流场压力p分布和黏性部分反映的壁面摩擦阻力系数Cf=τw/q∞(τw为壁面剪切应力)分布可深入认识壁温对气动力产生的内在影响。如图6(c)所示,等温壁流场和绝热壁流场在不同流向位置压力分布相同,而等温壁的壁面摩擦阻力系数略高于绝热壁的壁面摩擦阻力系数 (见图6(d)),来流动压相同且壁面摩擦阻力系数中的壁面剪切应力由黏性系数和速度梯度主导,表明在风洞试验状态下,壁温对气动力的影响主要体现在黏性部分。

将壁面气动力系数分为压力部分和黏性部分并单独积分:

(3)

(4)

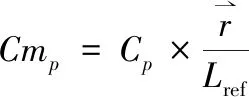
(5)

(6)

3 壁温对高空飞行状态计算影响

风洞试验状态壁温较低,来流总温与壁温相差较小,并且风洞吹风时间很短,壁温相对温升不高,数值模拟设置壁面温度为300 K得到的飞行器气动力与力矩计算足够精确。在真实飞行状态下,高超声速飞行器往往在高空环境飞行。一方面单位来流雷诺数相比地面实验条件小一个量级甚至多个量级,另一方面飞行器表面受到气动加热时间足够长导致热流大、温度高,此时壁温对高超声速飞行器气动力计算的影响更值得深入研究。选取飞行高度H为63.8 km、更高马赫数Ma为14作为计算飞行状态的工况,来流参数依据此高度下大气参数。为尽可能模拟真实飞行状态,将风洞试验状态计算模型放大10倍,放大之后轴长为4.27 m,底部面积为1.064 m2,网格及拓扑保持不变。

图8给出了高空飞行状态下气动力与力矩系数随攻角演变,其中300～9 000 K为在等温壁面条件下的壁面温度,同时给出了绝热壁面条件的计算结果。在绝热壁面条件下,类HTV-2飞行器表面温度分布可分为头部的高温区[9 000 K,10 000 K]、翼身的中温区[7 000 K,8 000 K]和底部的低温区[6 000 K,7 000 K],将3区温度分布赋予飞行器表面并设置等温壁面条件,得到图8中分区等温的计算结果。

图8(a)为轴向力系数Cx计算结果,可以看出壁温对轴向力系数Cx的影响相当显著,随着壁温的升高,在本文中计算攻角下轴向力系数逐渐增大。在绝热壁面条件下,壁面温度在[6 000 K,10 000 L]之间,但翼身大面积温度位于[7 000 K,8 000 K]之间,因此绝热壁轴向力系数略大于等温壁面T=7 000 K计算结果,且小于等温壁面T=9 000 K计算结果。分区等温的轴向力系数Cx计算结果表明在壁面温度相差范围不大的情况下,依据实际壁温情况采用壁温分区的方法计算得到的轴向力系数与直接采用绝热壁面条件结果相同。图8(b)、图8(c)分别给出了高空飞行状态下法向力系数Cy与俯仰力矩系数Cmz随攻角演变,由图可知,各个壁温条件下法向力系数Cy与俯仰力矩系数Cmz极为接近,表明小攻角条件下壁温对法向力系数Cy与俯仰力矩系数Cmz影响甚微。因此,综上分析可知,对于类HTV-2外形,在小攻角高空状态下,壁温对壁面轴向力系数Cx影响十分显著,而对法向力系数Cy与俯仰力矩系数Cmz影响甚微。

图9给出了小攻角条件下轴向力系数Cx随壁面温度演变。可以看出,轴向力系数随着温度升高表现出近似线性增长。为了评估温度效应作用在轴向力系数Cx的黏性分量或者压力分量。

图10给出了高空飞行状态轴向力系数Cx的黏性和压力分量随壁温演变,其中实线实心符号代表压力分量,虚线空心符号代表黏性分量。由图可知,Cx压力分量随着壁温的提高近似线性增长,且其值与攻角成负相关。Cx黏性分量在壁温较低时(T≤3 000 K)变化并不明显,随着温度逐渐升高(T>3 000 K),其值缓慢增长,并且Cx黏性分量与攻角之间未发现明显关联,其值始终在小范围内波动。

图1 类HTV-2模型示意图

图2 数值模拟网格示意图

图3 数值计算与风洞试验气动力结果对比

图4 等温壁面条件流向不同截面压力分布

图5 绝热壁面条件流向不同截面压力分布

图7 壁温对气动力压力分量和黏性分量的影响

图8 高空飞行状态壁面气动力与力矩系数随攻角演变

图9 高空飞行状态轴向力系数Cx随壁温演变

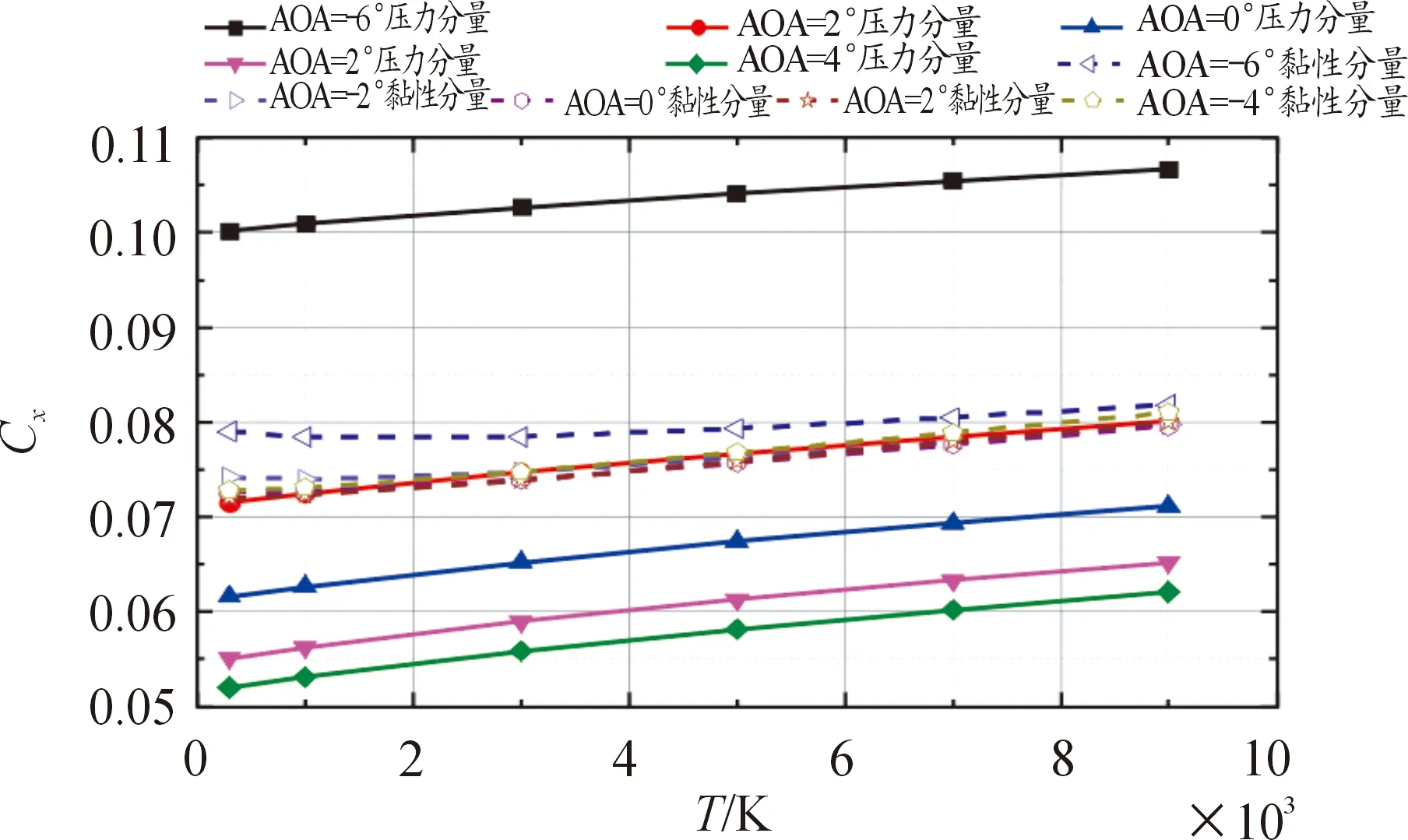
图10 高空飞行状态轴向力系数Cx的黏性和压力分量随壁温演变

为了定性研究在高空飞行状态壁温对边界层内流动特性的影响,提取中心对称面及壁面在不同壁温0°攻角下典型流向位置x=1 m和x=4 m的特征参数进行分析,如图11和图12所示。

图11 近壁特性参数(x=1 m)

图12 近壁特性参数(x=4 m)

可以看出,壁温显著影响边界层内温度分布,壁温越高,边界层内温度也随之增高。值得注意的是当壁温小于等于 5 000 K时,边界层内高温气体加热飞行器壁面,当壁温大于等于7 000 K时,飞行器壁面加热边界层内高温气体,而对于绝热壁条件壁面热流量为0。由于当地声速与温度成正比,因此马赫数与温度成反比,表现为壁温越高其边界层内相应位置马赫数越小,并且速度边界层越厚。迎风面压力随壁温升高保持不变,背风面压力随壁温升高持续增大,因此飞行器表面压差阻力随壁温升高而增大,造成轴向力系数Cx压力分量与壁温成正比。对于类HTV-2外形,在0°攻角条件下,壁温对摩擦阻力系数cf存在影响,但在流向不同位置处影响规律不同。

图13给出了不同壁温条件下壁面极限流线。从图13中可以看出,背风面①区压力随着温度的升高逐渐增大,并且范围逐渐扩大,而背风面②区压力随着温度升高基本保持不变,因此当壁温较低时,侧缘中段的流体粒子沿着侧缘外缘向底部流动,当温度逐渐升高,侧缘中段的流体粒子在压力梯度作用下逐渐向中心线聚拢。显然壁面温度的不同改变了背风面压力的分布,致使边界层内流体粒子运动轨迹发生改变。

图13 壁面极限流线

4 结论

为了研究壁温对高超声速飞行器气动力计算的影响,数值模拟了风洞试验状态和高空飞行状态下气动力和边界层内特性参数,得到的结论如下:

1) 对于类HTV-2面对称升力体外形,在小攻角飞行条件下,壁温不同对法向力系数和俯仰力矩系数影响较小,而对轴向力系数影响显著。

2) 对于数值模拟风洞试验状态,由于预测壁温与真实试验壁温较低且变化范围不大,壁温通过作用在边界层内的黏性剪切应力对轴向力系数产生微弱影响。

3) 对于数值模拟高空飞行状态,在更高马赫数飞行条件下,壁温不同对边界层内的黏性剪切应力和压力均产生影响,需要模拟飞行器作长期定常飞行时的温度以得到精确的气动力预测结果。