数据驱动的交通信号控制感知—评估—诊断—优化闭环技术（三）：运行评估

文图｜吴浩 骆旅舟 朱宏 唐克双

交通信号控制运行评估可直观反映各项运行状态感知指标的优劣程度，为问题诊断提供重要的参考依据。本文在借鉴现行标准以及行业企业的运行评估业务的基础上，介绍了一种交通信号控制运行评估技术，梳理了交通信号控制运行状态感知指标体系中用于评估的指标，通过融合预优化技术与交通流状态重构等技术，提出了各项评估指标参考区间的计算方法，进一步对感知指标进行评估打分与分级，并举例说明了部分指标的运行评估方法。

一、背景与目标

交通信号控制状态感知可全面、客观和精细化地反映交通运行现状。然而，在实际工作中，交通管理者通常难以仅凭状态感知指标的数值来确定信号配时方案的优劣，即在当前交通需求条件下，状态感知指标究竟是偏高还是偏低。运行评估的主要功能是确定状态感知指标的合理参考区间，对其进行评分和分级，为交通管理者提供量化的评估标准。

目前，标准规范仍是交通实践中最为常见的评估依据。《道路交通拥堵度评价方法》（GA/T 115/——2020）、《城市交通运行状况评价规范》（GB/T 33171——2016）等现行国家、行业和地方标准，分别面向单点、干线等不同场景，提出了一系列用来描述交通运行状态的评估指标，是交通管理者开展运行评估工作时最为常见的评估依据之一。此类运行评估方法反映的往往是一段时间内交通运行状态的总体定性描述（畅通、轻度拥堵、中度拥堵等），评估粒度较粗。此外，此类方法主要通过对最大车均延误、行程时间等常见感知指标二次计算，得到交通运行状态的评估结果，其有限的评估指标难以全面反映交通运行现状。

近年来，伴随我国智能交通市场与信息化技术的发展，一部分行业企业结合其软硬件优势，提出了自身所特有的评估方法。例如，百度地图提出了面向城市路网场景的“拥堵六维特征画像”，包括了严重拥堵路段里程占比、高峰拥堵指数在内的多项用来刻画区域级/城市级拥堵特征的感知指标，并采用各项指标在同类城市中的排名计算其评估分值；高德地图基于高峰平均速度、常发拥堵路段里程比在内的六项感知指标，提出了综合指标“交通健康指数”，并使用熵权法确定各项指标的权重，基于历史数据计算综合指标的参考区间，通过计算感知指标与参考区间的贴近程度获取评估分值。然而，此类方法多假设评估指标具有单调性，即指标值应越大越好或越小越好，较少从当前交通供需关系出发确定状态感知指标的合理参考区间。

二、交通信号控制运行评估

针对当前运行评估未成体系以及参考区间与现实场景脱节的现状，本文在借鉴现行标准及行业企业的运行评估业务的基础上，提出了一种交通信号控制运行评估方法，适用于单点、干线和路网三个场景，可更好地服务于运行感知指标的定量评价以及后续的问题诊断和方案优化。

（一）总体技术流程

交通信号控制运行评估方法主要包括指标分类、预优化以及参考区间计算三个步骤，总体技术流程如图1所示。首先，依据各项状态感知指标的定义及适用场景，将信号控制状态感知指标体系划分为用于评估指标与其它指标两个类别，对于用于评估指标，根据其运行评估参考区间来源的不同，进一步分为标准规范、模型计算和仿真推演三类。然后，利用预优化技术，获取在当前交通需求下合理的信号配时方案，并将其作为基准，计算各项用于评估指标的参考区间。在此基础上，通过比较各项用于评估指标的感知结果与相应的参考区间，可计算出各指标的评估分值（0 ～100）和分级（优、良、中、差）。

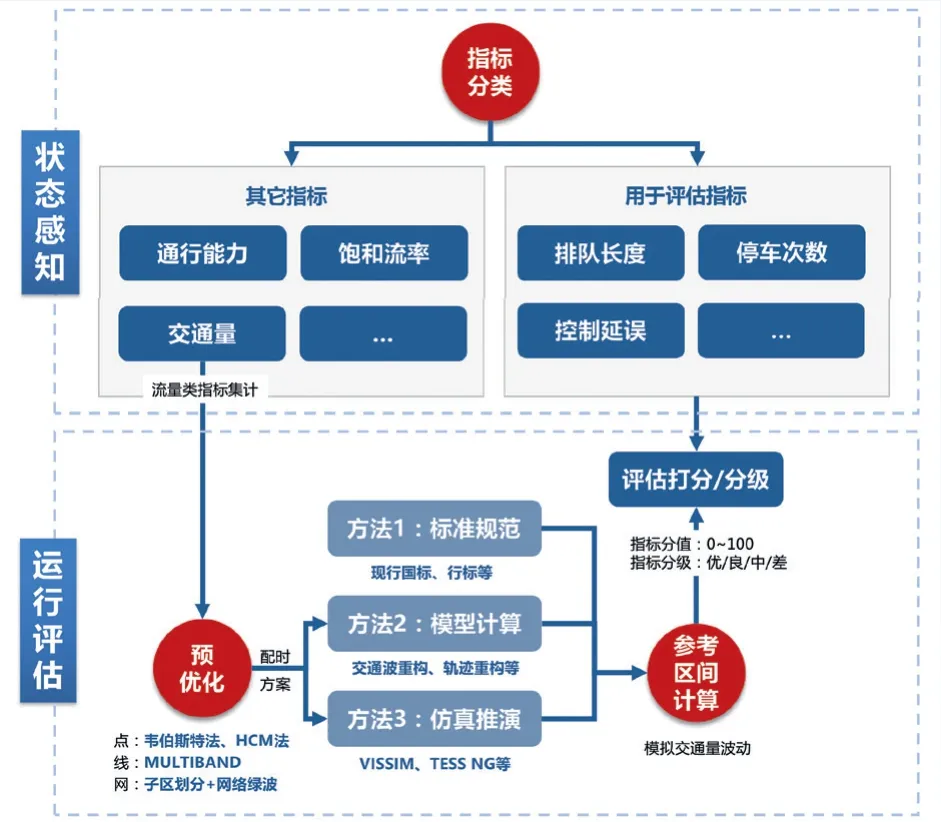
图1 交通信号控制运行评估总体技术流程

（二）指标分类

状态感知指标反映了交通供给与交通需求的共同作用结果，因此，单方面反映交通供给（交叉口通行能力、干线通行能力等指标）或交通需求（交叉口交通量、高峰小时交通量等指标）的感知指标无对应参考区间，此类指标称为其它指标，如表1 所示。对于用于评估指标，其参考区间的主要来源可分为如下三类：

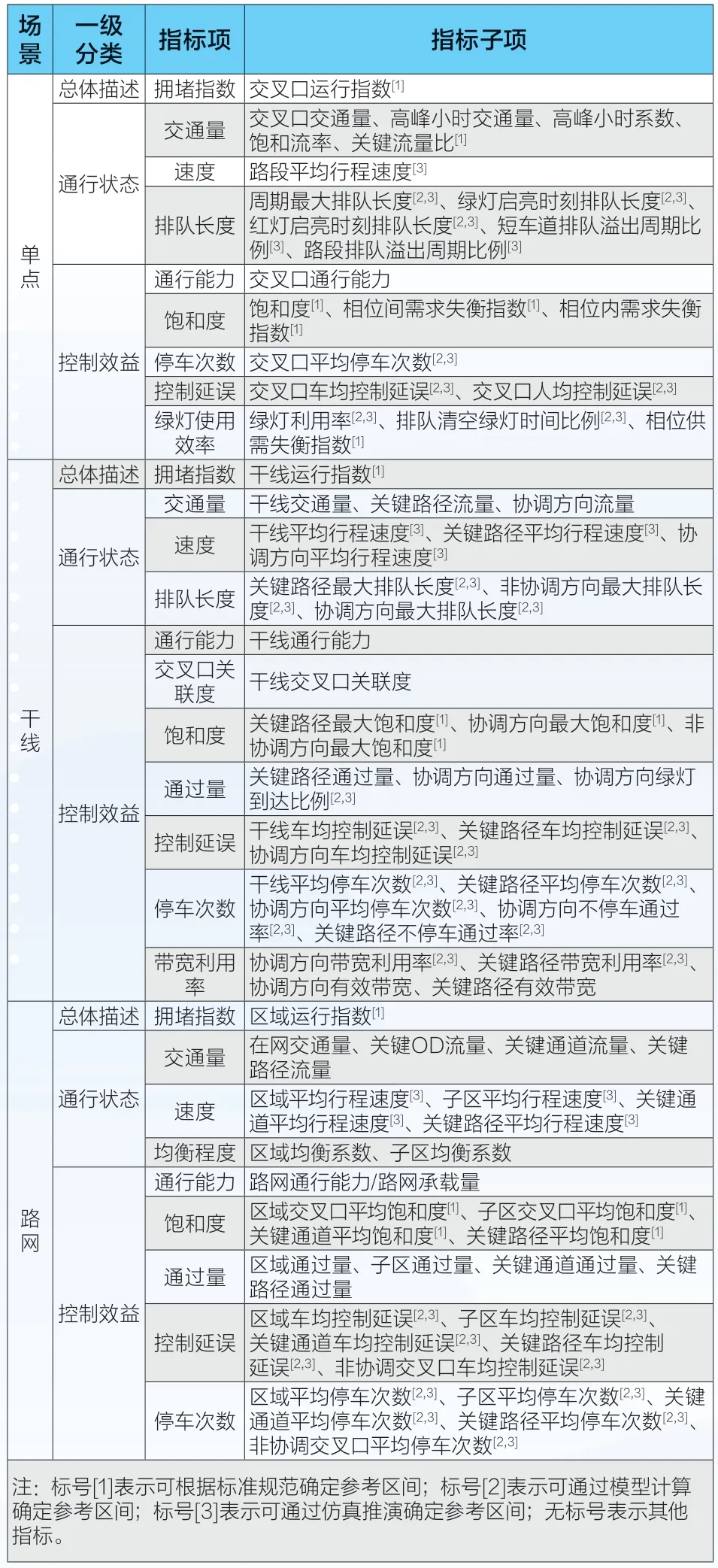
表1 交通信号控制运行状态指标评估体系

（1）标准规范（由[1]表示）：相关研究表明，当饱和度处于0.8 ～0.9 的实用限值时，系统处于较好的运行水平，因此，饱和度及其相关指标（相位间需求失衡指数、相位供需失衡指数等）的参考区间可直接基于实用限值确定；此外，部分收录在标准规范中的指标（交叉口运行指数、干线运行指数等）的参考区间也可直接确定。此类方法可提供少部分感知指标的运行评估参考区间。

（2）模型计算（由[2]表示）：在已知信号配时方案和交通需求的情况下，可以利用交通流状态重构模型，如交通波重构和车辆轨迹重构等，计算各项指标的基准值，作为感知指标的评估依据。同时，考虑到交通量的波动性，计算出各项指标的参考区间。此类方法为感知指标的运行评估参考区间的主要来源。

（3）仿真推演（由[3]表示）：在已知信号配时方案和交通需求的情况下，可基于仿真软件（VISSIM、SUMO、TESS NG 等）对所研究场景下的交通流状态进行仿真推演，直接获取各项评估指标的参考值及参考区间。部分涉及频率的状态感知指标（短车道排队溢出周期比例等）的运行评估参考区间只能通过此方法获得。

（三）预优化

无论是模型计算还是仿真推演，都需要已知信号配时方案，且合理的信号控制方案是运行状态精准评估的前提。因此，本文引入了预优化的概念。在计算各项用于评估指标的参考区间之前，对所研究的交通场景（单点、干线或路网）进行初步的信号配时优化，有助于确定在交通供需关系良好的情况下，各指标应该处于的数值范围。区别于本闭环技术体系的“方案优化”模块，预优化模型的选取应注重轻量化和可实施性。

针对单点，预优化模型可采用基于最小延误的韦伯斯特法或基于饱和度的HCM 法，其输入为流量及配时约束，输出为交叉口的信号配时优化方案。其模型思路为：首先确定交叉口的绿灯间隔时间与信号总损失时间，计算所有相位关键车道组的流量比之和，并使用最优周期长度公式计算周期时长，再根据各相位关键车道组的流量比确定其绿灯显示时间。

针对干线，预优化模型可采用基于带宽最大的协调优化模型（MULTIBAND 等），其输入为流量、绿信比、排队清空时间等参数，输出为干线的信号控制协调方案，包括各交叉口的信号配时优化方案及协调相位差。其模型思路为：通过协调干线上连续交叉口的相位差，最大化协调方向的连续绿波带宽，使得尽可能多的车辆能以车队形式不停车通过各个交叉口。

针对路网，预优化模型可采用基于控制子区划分的区域协调控制方法（网络绿波模型等），其输入为各交叉口的流量、绿信比、排队清空时间等参数，输出为路网的信号控制协调方案。其模型思路为：将路网分成若干相对独立的控制子区，在各控制子区内部采用协调优化模型（MULTIBAND 等）并添加额外约束，允许干线之间交叉或形成闭环，从而实现路网的协调优化。

（四）参考区间计算

模型计算和仿真推演两种方法都可以基于当前的交通供需关系来获取各项评估指标的参考区间，其基本逻辑相似，即根据原始的交通需求和预优化方案，还原研究场景（单点、干线、路网等）的交通流状态，得到指标的评估参考值，并将此值视为在交通供需关系良好的条件下的最优值（分值记为100）。此外，考虑到交通量的波动性，分别增加或减少交通需求20%，并使用同样的交通流状态重构方法，得出各项评估指标的上下限值（分值记为60），即评估指标的参考区间。两类方法的区别在于对交通流状态重构方法的不同，前者通过模型计算，如交通波重构和轨迹重构等，来获得各项用于评估指标的参考区间。而后者直接基于仿真软件，通过仿真推演直接输出各项用于评估指标的参考值及参考区间。

以单点场景下的“周期最大排队长度”指标为例，该感知指标的参考区间可以通过模型计算或仿真推演获得。本文简要介绍模型计算方法。首先，在已知交通需求和预优化方案的基础上，计算各个流向在周期内的到达车辆数，通过标定车辆的饱和车头时距、排队密度以及加入排队前后的车辆速度，进一步推导出集结波与消散波的速度，从而获取“周期最大排队长度”指标的参考值；随后，考虑到交通量的波动性，分别将周期内的到达车辆数增加和减少20%，并使用相同的方法进行计算，将结果作为指标的上下限值，如图2（a）所示。

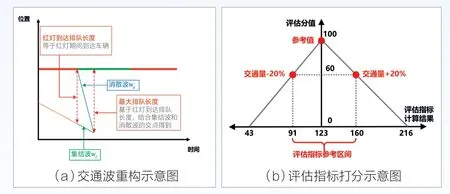
图2 评估参考区间及打分示意图

在获得用于评估指标的参考区间后，可以进一步对各项指标的感知结果进行评估和打分。通过对参考值与参考区间上下限进行线性拟合，可以将感知指标的值映射为介于0 和100 之间的数值，以实现对感知指标的打分。为了更清晰地展示，可以将分值分成四个等级：优（80 ～100）、良（70 ～80）、中（60 ～70）、差（0 ～60），如图2（b）所示。

三、交通信号控制运行评估算例

本文以单点场景下的“周期最大排队长度”指标为例，阐述了交通信号控制运行评估方法，其他用于评估指标可以采用类似的方法进行计算。

首先，结合交通检测数据与韦伯斯特模型，计算得到该单点的预优化方案。在这个方案中，信号周期长度为120 秒，所研究流向的红灯时长为80 秒，绿灯时长为38 秒，黄灯时长为3 秒。此外，基于历史数据的标定结果表明，车辆加入排队和离开排队的速度均为50千米/时，车辆排队车头间距为8 米，饱和车头时距为2 秒，流量为500 辆/时。然后，可计算出集结波的波速为1.21 米/秒，消散波的波速为5.62 米/秒。周期最大排队长度在绿灯的第22 秒出现，长度为123 米。

在此基础上，进一步将交通量减小20%，降至400辆/时，使用相同的方法计算得到周期最大排队长度为91 米，出现在绿灯的第16 秒，并将此值作为“周期最大排队长度”的参考区间下限。然后，将交通量增加20%，增至600 辆/时，计算得到周期最大排队长度为160 米，出现在绿灯的第28 秒，并将此值作为“周期最大排队长度”的参考区间上限。因此，在所研究的时段内，“周期最大排队长度”的评估参考区间为91 米～160 米，参考值为123 米，计算过程如图3 所示。

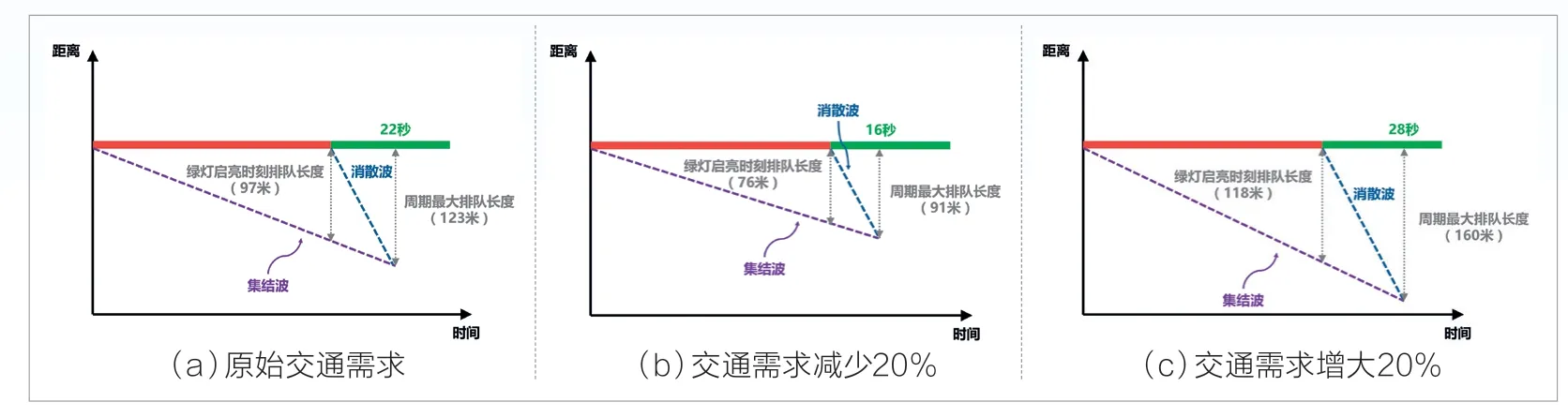
图3 交通波重构过程示意图

假设在该时段内，“周期最大排队长度”的感知结果为140 米，则可基于评估参考区间与线性插值方法，计算出该指标的评估分值为82 分，对应的评估等级为“优”。