基于模型辨识的新型牵引供电系统直流馈线保护原理

和敬涵，廖南杰，李 猛，卫云辉，郭旭刚，李 强

（1.北京交通大学 电气工程学院，北京 100044；2.中国铁道科学研究院集团有限公司机车车辆研究所，北京 100089）

0 引言

随着城市化进程的不断加快，以地铁为代表的城市轨道交通建设得到了快速发展，运营里程和耗电量不断增加。 “双碳”目标下，绿色低碳成为地铁牵引供电系统的发展方向［1-2］。而常规牵引供电系统只能实现能量的单向流动，再生能量利用率低，难以较好地实现新能源并入。随着电力电子技术的快速发展，基于电压源换流器（voltage source converter，VSC）的柔性直流牵引供电系统可实现双向供电，且控制灵活，提高了供电可靠性和再生能量利用率，可提升新能源消纳水平，具有广阔的发展前景［3-5］。然而，新型系统下线路发生故障后相邻的多个换流器均会向故障点馈入电流，如果保护不及时动作，易导致多个换流器因过流而闭锁，扩大故障影响范围，这对直流馈线保护提出了全线故障快速动作的要求。同时，由于机车启动瞬间，馈线电流同样会快速增长，机车启动电流在幅值及变化率上与远端故障电流存在一定的相似性，直流馈线保护如何在极短时间内实现全线速动并可靠区分启动电流，面临严重挑战。

目前，地铁直流馈线主保护主要采用大电流脱扣保护、电流变化率和电流增量（DDL）保护等。文献［6］指出了直流馈线保护一些重要参数的计算方法，并针对DDL 保护的整定数值进行了详细研究。文献［7］分析了DDL 保护的局限性，并在传统DDL保护的基础上进行了改良，一定程度上减小了列车启动对保护装置的影响。但DDL 保护在发生远端短路故障时动作速度慢，难以满足新型牵引供电系统保护需求。文献［8］采用Mexh小波变化提取电流的时间常数变化特征来区分远端短路故障和机车启动过程，但其时间窗较长。文献［9］利用经验模态函数重构能量熵来识别列车启动电流和远端短路故障电流，但工程应用效果有待验证。

上述文献针对常规牵引供电系统下远端故障电流和机车启动电流区分难题，主要利用电流特征进行辨别，易受故障位置及过渡电阻的影响，在一定程度上牺牲了保护的速动性，难以完全适应新型牵引供电系统。文献［10］针对新型地铁牵引供电系统提出了一种利用5G 通信技术的多端电流差动保护方案，该保护方法利用机车与牵引变电所之间电气量信息的快速交互，实现了全线速动，但目前5G技术在地铁中的应用还存在一定的技术瓶颈和经济限制。

虽然柔性直流输电技术在我国已经取得了巨大发展，且工程中柔性直流线路主要以行波保护作为主保护［11］，但行波保护为了捕捉故障信息需要高采样频率，对于长度较短的地铁线路在采样频率方面提出了更高要求，实际工程难以实现。因此，柔性直流输电工程中采用的行波保护并不适用于柔性直流牵引供电系统下的地铁直流馈线保护。

针对高压交直流输电线路，基于模型参数识别的保护原理已被提出［12］。模型参数识别保护是利用全时域或频域的故障信息计算识别被保护元件的参数，构成保护判据，理论上不受故障暂态的影响，可靠性高、动作速度快。文献［13-14］针对基于电压源换流器的高压直流输电（voltage source converter based high voltage direct current，VSC-HVDC）线路的RLC 模型列写时域微分方程求得故障距离及线路元件参数，但需要函数迭代，计算量较大。文献［15］提出一种频变参数电缆线路电流差动保护新原理。文献［16］提出一种基于阻感模型和电容模型的纵联保护原理。文献［17-18］提出了基于模量的线路模型识别纵联保护新原理，利用线路电容、电感模型识别区内外故障。但上述方法并没有考虑机车启动过程，不能直接应用于新型牵引供电系统直流馈线保护。

为了能快速准确地区分机车启动电流和故障电流，本文参考模型参数识别思路，从模型辨识的角度来寻找两者差异；从机理上揭示了短路故障和机车启动的暂态模型差异，引入方差系数的思想，提出了一种基于模型辨识的新型牵引供电系统直流馈线保护原理。该保护原理利用模型参数的统计分布规律，可准确区分短路故障和机车启动过程，快速判别故障，理论上不受过渡电阻影响。

1 柔性直流牵引供电系统特性分析

直流牵引供电系统由牵引变电所（降压变电所和整流机组）和牵引网系统（接触网或走行轨、馈线、回流线）两部分组成。我国地铁工程建设目前大部分采用24 脉波整流器，将城市中压交流电转化为750 V 或1 500 V 直流电供机车使用，这种整流方式结构简单、成本低，但无法实现能量双向流动，不利于新能源并网。柔性直流牵引供电系统利用VSC实现能量双向流动，并灵活控制直流电压［19］，如附录A图A1所示。然而，柔性直流牵引供电系统直流侧故障特性也变得更加复杂。

1.1 故障分析

以最典型的双边供电方式为研究对象，供电网络如图1 所示。A、B 为相邻牵引变电所，当牵引变电所A、B 之间没有机车行驶时，两侧的直流馈线电流均为0。当牵引变电所A、B 之间有机车行驶时，两侧的直流馈线电流为一个较小的稳定值。同时在线路中间设置短路故障，i1、i2分别为牵引变电所A、B 的直流馈线电流；x为故障点与牵引变电所A 的距离；l为牵引变电所A、B 之间的线路全长；R、L分别为线路单位等效电阻、电感；Rf为过渡电阻；u1、u2分别为故障点左、右侧的直流侧电压。

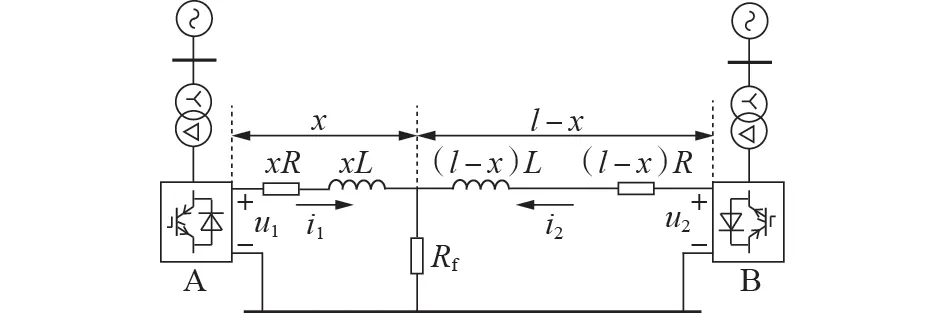
图1 双边供电示意图Fig.1 Schematic diagram of bilateral power supply

当地铁线路直流侧发生短路故障时，直流线路极间短路发生故障响应。短路故障发生初始阶段，由于电容放电电流远大于交流侧提供的短路电流，此时，忽略交流测的馈入作用，只考虑电容向故障点的放电作用，可得到如图2 所示的等效电路图。图中：y=x/l且y∈(0，1)，为基于2 个VSC 之间的直流线路总长度的归一化故障距离；Cdc为直流侧电容。

图2 电容放电等效电路图Fig.2 Equivalent circuit diagram of capacitor discharge

根据基尔霍夫定律，此时有：

由式（1）可得到如式（2）所示的直流侧电压四阶微分表达式。

式中：a、b、c、e为四阶微分方程的系数。

求解四阶微分方程式（2），得到如式（4）所示的直流侧电压表达式［20］。

式中：A1—A4为常数；αk、ωk分别为第k个阻尼分量的衰减系数、共振角频率。

同理，根据图1，在故障初始阶段，等效电路如图3所示。

图3 短路故障等效电路Fig.3 Equivalent circuit of short circuit fault

此时，故障处正负极之间的电压为u，流入故障处的电流为i，因此任意时刻故障电阻R1可表示为：

且任意时刻换流器正负极之间的电压为：

由上述推导可知，发生短路故障时，故障处正负极之间为一个过渡电阻。由于本文所提算法采样时间极短，因此过渡电阻可看成是一个阻值不变的恒定电阻。设故障时刻为0，根据电路理论，则故障发生后时刻T1、T2左侧换流器的电压、电流关系为：

式（7）仅含有2 个未知数，通过消去未知数x求解微分方程式（7）得：

因此，定义故障处正负极之间等效电阻Rd的算法为：

由于发生短路故障时故障处正负极之间为一个阻值不变的电阻，由式（7）可联立2 个方程求出故障处过渡电阻大小，并定义式（9）为等效电阻算法。由上述推导可知，发生短路故障时利用式（9）求得的等效电阻等于过渡电阻。因此在采样时间窗内不同时刻求出的等效电阻理论上是一个恒定的常数。

1.2 机车启动分析

对于直流牵引供电系统而言，在机车启动瞬间，机车可以看作是异步电机的启动过程，因此可以将机车等效成由电阻和电感串并连的感性负载，机车在启动瞬间，转差率s=1，由附录A 图A2 所示的异步电机等效电路可知，在启动瞬间机车等效电阻最小，因此启动电流最大。机车前端连接一套三相桥式逆变电路，由脉冲宽度调制（pulse width modulation，PWM）技术控制的6脉波绝缘栅双极型晶体管（insulated gate bipolar transistor，IGBT）换流桥组成，其等值电路如附录A 图A3 所示。因此机车启动瞬间的等效模型可由附录A图A4表示。

由上述推导可知，当机车启动时，由于VSC和电容会同时向机车馈入电流，此时直流侧电压会下降，根据图A4 可得到如图4 所示的机车启动等效电路。图中：u0为电容两端电压；iC为流入机车前端电容的电流；iL为流入机车内部电机的电流；C0为机车前端滤波电容；L0、R0分别为机车等效电感、电阻。

此时，机车处正负极之间的电压为u，流入机车的电流为i。根据基尔霍夫电路定理，可得到机车两端的电流、电压关系为：

求解上述一阶微分方程，可得到机车处正负极之间任意时刻机车电阻R2为：

因此机车启动后在时刻T1、T2有：

根据式（13）构建等效电阻算法，同理，消去未知数x求解微分方程得：

由以上分析可知，由于机车内部含有电感、电容等元件，当机车启动时，根据式（12）可知机车位置正负极之间为一个非线性负载，即机车处正负极电阻大小随时间变化。因此在机车启动初始阶段，由式（15）求得的等效电阻大小是一个随时间变化而波动的不稳定值。

1.3 区外故障分析

区外故障示意图见附录A 图A5。由图可见：牵引变电所B、C 之间发生短路故障时，故障处距牵引变电所B 的距离为x1，相邻牵引变电所A 也会向故障点馈入电流，导致馈线电流增长；此时牵引变电所A、B 正负极之间相当于开路，等效电路见图5。

图5 区外故障等效电路Fig.5 Equivalent circuit of out-of-zone fault

此时馈线电流相反，即任意时刻的i1+i2=0，可得：

可得发生区外故障时，任意时刻的Rd为：

由以上推导可知，当发生区外故障时，求出的等效电阻趋于无穷。为了快速、准确地识区外故障，同时简化方差系数保护判据整定，本文利用采样时间窗内馈线电流方向识别区外故障，以母线流向线路为正方向，即在采样时间窗内，若i1、i2在任意时刻均大于0，则为区内故障。若检测到的馈线电流小于或等于0，则为区外故障，保护返回。

由以上分析可知，当发生区内短路故障时，故障处等效电阻大小等于过渡电阻值，理论上是一个恒定的值。而当机车启动时，由于机车内部含有电容、电感等非线性元件，在启动过程中等效电阻大小随时间变化。由此引入方差系数，通过计算等效电阻方差系数来区分短路故障和机车启动过程，同时利用馈线电流方向来判断区内外故障。

2 基于等效电阻方差系数的保护方案设计

针对新型牵引供电系统短路故障电流和机车启动电流难以区分的问题，本文不局限于从电流幅值或特征的角度去分析问题，而是从机理上分析两者，通过采集电流、电压数据，构建等效电阻的统计分布模型，并利用方差系数的差异构造保护判据。

2.1 基于等效电阻方差系数的算法推导

由上述推导可知，当发生区内短路故障时，利用式（9）求出的等效电阻等于过渡电阻值，理论上在不同时刻求出的等效电阻为一个恒定的常数，考虑差分求导误差以及其他因素的影响，求出的电阻值会有较小的波动。而对于机车启动过程，由式（15）可知，利用此算法求出的等效电阻是一个随时间波动的不稳定值。

由以上分析可知，可利用式（9）计算不同时刻等效电阻的大小，若电阻值波动很小，则是短路故障；若电阻值波动很大，则是机车启动过程，由此引入方差系数的概念。通过计算等效电阻方差系数的大小来区分故障电流和机车启动电流。

本文利用故障后n 个采样点的数据对电阻进行方差计算，可得到等效电阻方差系数s2r表达式为：

式中：Rm为采样点m处的等效电阻计算值；Rˉ为n个等效电阻的平均值。

由图A5可知，可通过检测采样时间窗内馈线电流的正负来辨别区内外故障，若在任意时刻馈线电流均满足式（19），则为区内故障，否则为区外故障，保护返回。

2.2 基于等效电阻方程系数的保护判据

本文根据故障发生或机车启动后直流馈线电流变化率构成保护启动元件，启动判据为：

式中：di/dt为换流站直流馈线电流变化率；kset为设定的电流变化率阈值。根据电容的放电特性以及大量不同位置下机车正常行驶的仿真实验，kset设定为1 000 A／s。

图6 保护原理流程图Fig.6 Flowchart of protection principle

3 影响因素分析

下面对过渡电阻、采样频率、噪声干扰、同步误差、钢轨的集肤效应、杂散电流等影响因素进行理论定性分析。

3.1 过渡电阻与电弧

由以上分析可知，本文采用的算法可通过微分方程精确计算过渡电阻值，以此来构建方差系数的故障判别依据。因此，本文所提算法在理论上不受过渡电阻值的影响。同时，由于地铁可能发生电弧故障，而电弧的弧伏安特性受电弧长度、电极材料、气体介质、环境压力等因素的影响，发生电弧故障时不可避免地会对方差系数造成影响。在线路发生电弧故障时，由于电弧故障的发展时间为几十毫秒到几秒，但本文所选取的时间窗极短，因此当电流快速增大时，电弧电阻还来不及变化，此时伏安特性与一般直流电阻的特性相似，为一条直线，则在所选取时间窗内可将电弧电阻看成线性电阻，因此本文所提保护方法在发生电弧故障时依然能可靠动作。

3.2 采样频率

本文采用差分代替微分计算电流导数，因此理论上采样频率越高，电流的导数计算值越精确，则对故障过程过渡电阻值的计算也越精确。为了选取合适的时间窗，保证保护的速动性，同时兼顾算法的精确性，本文选取3 ms的时间窗。

3.3 噪声干扰

噪声是通信过程中客观存在、无法消除的，它是在正常信号上叠加的一个随机过程，会引起信号波形失真，导致误判，对通信质量产生影响。由于本文是通过求解微分等式求取方差系数，因此噪声的加入会使信号偏离正常值，导致所列微分方程等式不满足恒等关系，引起一定的等效阻抗计算误差，但由于方差系数是描述数据的离散程度，因此，所提保护算法可耐受测量元件正常范围内的噪声。

3.4 同步误差影响

由于本文所提保护算法需要用到对端的电流数据，因此对于电流信号的传输而言可能会出现同步误差，目前地铁普遍采用基于全球定位系统的地铁时钟同步系统为通信系统及其他各有关系统提供统一的标准时间信号，一般认为同步误差在2 μs以内。为了验证所提算法的耐同步误差能力，本文以一个采样间隔，即100 μs的同步误差进行仿真验证。

3.5 钢轨集肤效应及杂散电流

钢轨除了作为轨道供机车正常行驶外，还具有回流的作用，由于钢轨的制作材料以及结构比较特殊，这导致钢轨的磁导率变高，在导通电流后，钢轨内部会存在集肤效应，使钢轨的阻抗在通电的过程中发生变化。同时，由于钢轨对地并不能完全绝缘，会有部分电流渗入通过大地，这种渗入地下的电流称为杂散电流。在上述变化下，线路将不满足RLC模型，导致发生故障时求得的等效电阻不精确，进而影响方差系数。因此需考虑钢轨的集肤效应及杂散电流对保护产生的影响。

4 仿真验证与分析

本章通过仿真对各影响因素进行定量分析。在PSCAD／EMTDC 仿真平台中搭建如图A5 所示的750 V 柔性直流牵引供电系统模型，以北京地铁某线路参数为例，两换流站之间的距离为3 km，L=1.79 mH／km，R=0.03 Ω／km。换流站均采用VSC结构，机车启动过程采用恒转速控制，额定功率为180 kW。相邻牵引变电站的距离为3 km，采样频率为10 kHz。换流器出口处电容为0.02 F，机车前端滤波电感为0.006 H，滤波电容为0.006 F。

4.1 短路故障与机车启动分析

以典型的双边供电方式为例，牵引变电站A、B之间的距离为3 km，在与牵引变电站A 相距1、2、3 km 处分别设置双极短路故障和机车启动过程。采集故障发生后的3 ms 数据，即30 个采样点的数据，计算这30 个采样点对应的等效电阻方差系数。故障工况和机车启动对应的等效电阻数据波动图如附录A 图A6 所示。由图可知，在故障发生后的3 ms采样数据中，求出的等效电阻波动较小，而对于机车启动过程，求出的等效电阻为一个波动较大的变量，两者的统计分布规律截然不同。同时，在线路不同区段设置短路故障和机车启动，计算2 种情况下的方差系数，保护结果如表1 所示。由表可知，机车在线路不同位置启动均不会导致保护误动作。

表1 短路故障与机车启动保护判别结果Table 1 Protection judgment results of short circuit fault and locomotive start-up

上述仿真结果表明：本文所提保护方法可有效区分故障电流和机车启动电流。

4.2 耐受过渡电阻能力与电弧故障分析

由上文分析可知，本文通过微分方程可求解发生故障时过渡电阻的大小，因此本文所提保护原理理论上不受过渡电阻的影响。为了验证本文所提保护方法的耐受过渡电阻能力以及电弧故障的影响，在不同区段设置过渡电阻为0.1、10、100 Ω的短路故障，同时在不同位置设置电弧故障。本文所提保护方法的保护动作结果如附录A 表A1 所示。由表可见：在区内设置不同过渡电阻的短路故障与电弧故障时，方差系数均远小于阈值，保护可靠动作；区外故障下保护均不会误动作。

4.3 噪声干扰分析

本文所提保护方法利用时域微分法求取等效阻抗方差系数。因此，当信号传输过程中存在噪声时会对微分等式造成一定影响，从而使方差系数增大。因此需要考虑不同信噪比噪声干扰下保护的可靠性。在线路不同区段加入不同信噪比的高斯白噪声，保护结果见附录A表A2。由表可知，对线路不同区段加入30、40 dB 高斯白噪声后，方差系数增大，但依然远小于动作阈值，即本文所提保护方案在一定噪声情况下依然能够准确识别故障并可靠动作。

4.4 同步误差分析

为了验证本文所提保护方法的耐受同步误差能力，现取一个采样点的同步误差（100 μs）验证本文所提保护方法，对应的线路不同区段故障下的保护动作结果如附录A 表A3所示。由表可知，在同步误差为100 μs 时保护依然可靠动作。因此，本文所提保护方法具有一定的耐受同步误差的能力。

4.5 钢轨集肤效应及杂散电流影响因素分析

本文采用工程中普通使用的定时间常数法建立钢轨的等效模型，并根据北京地铁某线路设置相邻牵引变电所的站间距离为3 km。钢轨的等效电阻值为0.03 Ω／km，钢轨的等效电感值为1.79 mH／km，钢轨的对地电阻为3 Ω／km。根据以上参数利用PSCAD／EMTDC 仿真平台搭建如附录B 图B1 所示的钢轨等效模型，并在此基础上建立大地及杂散电流的电气模型。本文根据附录B 表B1 和表B2 的钢轨参数建立如附录B 图B2 所示的Π 型钢轨回流模型，并在线路不同区段设置短路故障。保护判别结果如附录B 表B3 所示。由表可知，在考虑钢轨肌肤效应以及杂散电流的情况下，在线路不同位置发生故障时，保护依然能可靠动作。

4.6 保护动作时间及DDL保护动作特性分析

本文所提保护算法的动作时间主要包括保护启动时间、对端电流的数据传输时间、保护算法的计算时间。以相邻牵引变电站之间的线路全长为3 km为例分析本文所提保护方案的动作时间。

保护启动时间即保护感受到电流变化率大于阈值的时间，由于故障发生瞬间电流变化率最大，因此保护启动时间不超过0.3 ms。保护采用光纤通道进行数据通信，信号在光纤中的传播速度为200 km／ms，因此对于仅为3 km 的输电线路，考虑一定的裕度，延时不超过0.5 ms。本文所提算法采用的数据窗长为3 ms，算法的计算时间包括求解微分方程计算等效阻抗和计算方差系数所需的时间，根据计算机目前的计算能力，算法所需的时间不超过0.5 ms。

综合以上分析可知，考虑一定的裕度，本文所提保护的动作时间约为4 ms。

同时对DDL 保护在新型牵引供电系统下的动作特性进行分析，在远端设置金属性短路故障，得到远端故障馈线电流波形以及本文所提保护和DDL保护的动作情况如附录B 图B3 所示。由图可知：当发生远端短路故障时，DDL保护进入二段延时阶段，大约需要40 ms 才能切除故障，并在保护动作前，故障电流已到达峰值；而本文所提保护在发生故障后4 ms左右可靠动作。

同时在线路不同位置设置短路故障，得到2 种保护的动作结果如附录B 表B4 所示。由表可知：当发生近端短路故障时，DDL保护一段延时启动，在故障发生5 ms 左右即可切除故障，而在发生中远端短路故障时，DDL 保护进入二段延时动作，动作速度慢；而本文所提保护在线路不同位置发生故障时均能快速可靠动作，实现了全线速动。

5 结论

本文针对新型牵引供电系统直流馈线故障电流和机车启动电流难以区分的问题，从机理上分析了两者的本质差异，并提出一种基于模型辨识的直流馈线保护方法。大量仿真结果表明，本文所提保护原理可耐受100 Ω 过渡电阻，并且动作速度快，能在故障发生5 ms 内快速动作，同时具有30 dB 的抗噪声能力，在同步误差为100 μs 的情况下仍然能够实现保护的可靠动作。与DDL 保护相比，本文所提保护在远端短路故障下速动性更好、可靠性更高，解决了故障电流和机车启动电流难以区分的问题，实现了保护的全线速动。

附录见本刊网络版（http：//www.epae.cn）。