透水混凝土压缩试验及劈裂试验三维离散元分析

陈 晨，王亚萍，高文甫

（中国水利水电第三工程局有限公司,陕西 西安 710024）

1 引言

透水混凝土是一种典型的多孔材料,因其强度较低限制了在重载路面的推广应用；学者们尝试研究不同方法旨在提高其强度,但常规试验研究无法揭示宏观力学的内在作用机制。Cundall et al.[1-2]提出利用PFC 离散元颗粒流研究散粒材料的细观力学特性,弥补了连续介质力学模型计算非连续介质和大变形问题的不足。宿辉等[3]研究了生态混凝土不同细观力学参数对双轴压缩破坏的影响。栗浩洋[4]、Nsari 等[5]通过试验与PFC3D 模拟不同骨料尺寸、不同孔隙率透水混凝土性能的对比,较为准确地计算透水混凝土的最大抗压强度和应力应变响应。

本文将结合试验与PFC3D 模拟透水混凝土单轴压缩、三轴压缩以及压条劈裂,建立透水混凝土材料宏观力学特性与微观力学参数的关系,得到劈裂试验内在机制分析的替代方法。

2 本构关系

离散元是一种基于颗粒模拟砂土等非粘性介质微观力学的数值方法,其使用不同直径的刚性球体（3D）或圆盘（2D）对粒子进行建模,刚性球体或圆盘在它们的接触点上相互连接时,接触被赋予刚度和摩擦系数的值。PFC 计算时,首先使用力-位移方程将颗粒间接触产生的位移转化为颗粒的接触力,之后根据运动方程计算以及更新颗粒的位移,同时计算颗粒所受的体力,以实现每步计算时的循环。PFC 模型使用的粘结模型有线性接触Coulomb 摩擦模型、接触粘结模型、平行粘结模型三种。线弹性接触模型,在此基础上加上摩擦系数即为Coulomb 摩擦模型,能够模拟砂土及卵砾石土的力学行为。接触粘结模型,只能在接触点传递力,颗粒间分别受法向及切向粘结力作用用来模拟粘性土颗粒的接触关系。平行粘结模型则使用接触平面上的一组弹性弹簧来抵抗粒子的旋转,这种粘结同时可传递力和力矩,适用于模拟混凝土骨料颗粒间水泥的粘结力学性能。

颗粒流离散元方法的边界条件可以由刚性墙体来控制。颗粒-颗粒及颗粒-墙体接触关系见图1,其中,Cs和Cn为法向和切向的粘结力,对于无粘性土Cs和Cn取值为零, fμ为颗粒滑动摩擦引起的摩擦力。

图1 颗粒-颗粒及颗粒-墙体接触关系示意图

3 透水混凝土压缩试验和劈裂试验PFC3D数值模拟

3.1 数值模型建立

3.1.1 PFC3D 三轴压缩数值模型建立

以PFC2D 本构模型为基础,延伸至PFC3D 建立三轴压缩数值试验模型。

（1）建立六面体模型,模型6 个墙体的摩擦系数为零,侧面墙体的法向刚度为球体平均刚度的βx=βy倍,上下墙体法向刚度为球体平均刚度的βx=βy=βz倍。

（2）以伺服机制原理为基础,通过控制6 个墙体速度,达到施加围压和垂直应力的目的。伺服行为是通过控制墙体的伺服误差ε实现,即当（σ-σt）/σt≤ε时,相应的速度为0。

（3）试样的加载通过以速度vp移动上下墙体实现。为了消除一次施加瞬时速度引起的惯性力影响,速度vp是通过几个阶段的N 次循环逐渐实现的。

（4）在三轴试验过程中,通过监测偏应力σd确定试验是否完成。对于有接触连接的岩体,σd首先增加到一定数值（最大值）,随着试样的破坏然后降低,当σd≤α（σd）max时,试验结束,α为试验结束系数。

在完成三轴压缩PFC3D 数值试验后,相应的弹性模量E'和泊松比v 通过下式计算：

离散元计算中均采用笛卡儿直角坐标系,X、Y、Z 各轴方向,试样尺寸采用10 cm×10 cm×10 cm,透水混凝土压缩试验模型上下左右前后六面均为刚性光滑墙体边界。

3.1.2 PFC3D 压条劈裂数值模型建立

本文通过离散元软件PFC3D 建立试件尺寸为15 cm×15 cm×15 cm,压条尺寸为5 mm×5 mm×20 cm 压条劈裂数值模型,见图2。并应用程序生成有限元计算所需的数据文件,然后将生成的数据文件导入离散元软件中,来进行有限元计算和后处理。

图2 透水混凝土压条劈裂试验模型

图3 试验试件与离散元模型的受压破坏形态对比

3.2 模型计算参数

选定表1 中透水混凝土试验配比,其水胶比为0.25,孔隙率为0.18。以其28 d 抗压强度25.91 MPa 为宏观抗压强度,进行微观力学参数合理性测试,单轴压缩数值计算结果与试验结果相符时,可进行后续三轴压缩试验。经过测试采用表2 中参数时,两者抗压强度的结果相差0.7 MPa,从图2 可以看出其破坏形态也基本相同,最终确定了表2 种计算参数。

表1 透水混凝土试验配比和试验结果

表2 数值试验计算参数

3.3 设计工况

经过单轴压缩试验后,可对不同围压情况下的压缩试验进行了模拟计算。具体工况见表3。

表3 数值试验计算工况

4 数值计算结果分析

4.1 细观粘结力与宏观强度的关系（围压=0 MPa 的单轴压缩）

颗粒流离散元计算中,通过增大颗粒粘结强度,分析不同粘结强度放大倍数情况下透水混凝土宏观强度的提高程度。以表2 中单轴压缩数值试验的颗粒粘结强度为基数,选择提高至1.3、1.5、1.7、2.0 和2.5 倍五个量值计算确定宏观试样的单轴抗压强度,计算结果见表4。颗粒细观粘结强度可以视为透水混凝土骨料间砂浆的粘结强度,通过研究砂浆的细观粘结强度与透水混凝土宏观强度的关系,可以预测提高砂浆力学性能来提升透水混凝土宏观强度的效果。

表4 计算结果统计表

从图4 可以看出,骨料颗粒细观的粘结力与透水混凝土宏观抗压强度的关系呈非线性规律。砂浆粘结力提高倍数低于2.0 时细观强度与宏观强度间的关系呈线性y=x 的增长趋势；提高倍数高于2.0 时提高细观粘结力后宏观强度提升效果显著增强,呈y=1.54 ln（x）+0.90 的非线性趋势增长。

图4 细观强度与宏观强度的关系

4.2 三轴压缩试验

通过对不同围压条件下三轴压缩试验的模拟了,得到了其应力-应变曲线见图5。

图5 不同围压下压缩试验应力～应变曲线

由曲线数据得出：各个工况的峰值应力即破坏时刻的应力值见表5,并通过该数据绘制出压缩试验中不同围压下透水混凝土的强度包线见图6。

表5 不同围压下透水混凝土的峰值应力

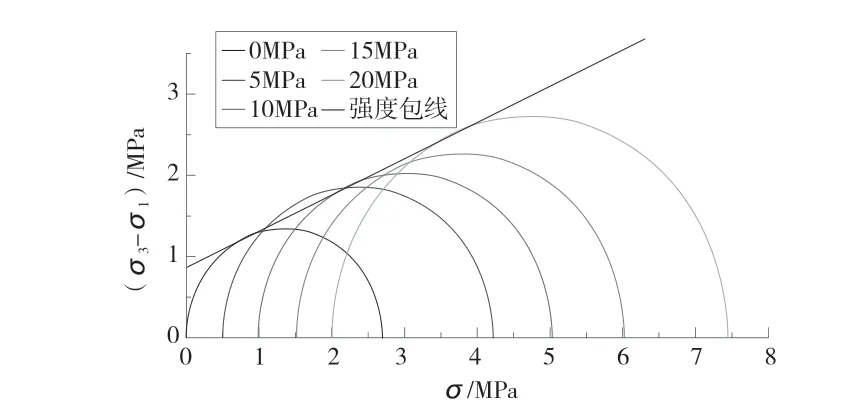
图6 不同围压下透水混凝土的强度包线

围压从5 MPa～20 MPa,透水混凝土的抗压强度提高了约2～3 倍,即结构可显著增强透水混凝土的力学性能。

由压缩试验中不同围压下透水混凝土的强度包线（图6）,计算得出透水混凝土的c、φ值分别为0.8 MPa、24°。

4.3 劈裂试验离散元数值计算结果

通过模拟研究单轴压缩载荷作用下透水混凝土试样劈压条劈裂破坏的过程,得到了其劈裂过程的应力～应变曲线,见图7。

图7 压条劈裂试验模型荷载～位移曲线

在劈裂抗拉试验中,当试件达到开裂荷载时,荷载迅速下降,透水混凝土呈脆性断裂。

混凝土劈裂抗拉强度：

试验的劈裂抗拉强度值为2.51 MPa,与试验结果相差0.08 MPa,基本相符。此结果表明PFC3D 数值模拟可以很好的模拟劈裂试验。

5 结论

本文通过使用PFC3D 三维颗粒流程序建立透水混凝土颗粒的接触模型,同时借助离散元软件对所建立方体透水混凝土数值模型进行压缩试验和压条劈裂试验,主要得出以下结论：

（1）骨料颗粒细观的粘结力与透水混凝土宏观抗压强度的关系呈非线性规律。砂浆粘结力提高倍数低于2.0 时细观强度与宏观强度间的关系呈线性y=x 的增长趋势；提高倍数高于2.0 时提高细观粘结力后宏观强度提升效果显著增强,呈y=1.54 ln（x）+0.90 的非线性趋势增长。

（2）围压从5 MPa～20 MPa,透水混凝土抗压强度提高了约2～3 倍,即结构可显著增强透水混凝土力学性能；得到了透水混凝土在三轴受压作用下的应力变形曲线和强度包线图,计算得透水混凝土的c、φ值分别为0.8 MPa、24°。

（3）通过模拟压条劈裂实验绘制力位移曲线图,分析计算得出混凝土劈裂抗拉强度为2.43 MPa,与试验结果相差0.08 MPa,提供了一种较为可靠的劈裂试验替代方法。