考虑组合荷载影响下扬州泵闸枢纽静动力特征研究

沈春林，田 扬

（1.南通市九圩港水利工程管理所,江苏 南通 226300；2.江苏省江都水利工程管理处,江苏 扬州 225200）

1 引言

水工结构中静动力响应特征不仅与上部结构有关,同时会在基础工程设计时考虑抗震效应[1-2],从桩土-上部结构组合荷载下,考虑静动力响应特征,更利于水工设计的全面性与实用性。王闺臣等[3]、李参等[4]为研究水闸结构静力稳定性特征,利用ANSYS 等有限元平台,从多工况下开展水工结构应力、位移分析,为水闸设施多工况下运营进行前期校验。曾欣等[5]、吴小龙[6]为研究水闸结构地震动响应特征,通过模拟输入地震波,探讨地震动荷载影响下水闸结构位移、应力以及加速度等响应特征,从动力响应水平评价水闸结构抗震设计效果。不论是静力特征分析或动力响应水平探讨,均是为水闸结构的运营提供参考服务,李密等[7]、张金堂[8]结合静动力特征两方面,通过对比分析水闸等水工建筑的静动力特征差异,评价结构设计关注重点,为工程建设提供实际依据。本文为研究扬州泵闸枢纽静、动力响应特征,不仅考虑无水工况下结构响应特征,也从流固耦合作用下分析桩土-上部结构与水体质量间关系。

2 研究概况

2.1 工程概况

扬州闸乃是扬州城区内长江、京杭运河重要水利控制枢纽,乃是一座闸泵站综合水利设施,泵站抽排、引设计流量分别为72 m3/s、29 m3/s,一方面承担着扬州市区生态用水供应,对古运河河道以及仪扬河进行水生态用水补充,乃是扬州市区打造水生态、景生态、湖生态以及人生态“四态化”城市发展的关键。由于扬州主城区围绕着长江、淮河水道建设,在汛期常出现警戒水位以及南部山区的山洪等自然灾害,不利于扬州市区防洪安全。扬州闸始建于1973 年,运营年限较长,部分水工设施出现老化“罢工”,自流抽排不畅,泵机运行效率降低等,为此,对扬州闸开展除险加固设计研究。该泵闸枢纽动力装置泵站机组设计为单、双向泵各2 台,且抽排设计流量分别为20.56 m3/s、16.57 m3/s,而抽引流量设计为15.17 m3/s,进水口断面宽度、高度分别为5.3 m、3.6 m。闸站内各项顶、底板结构,其静、动力安全稳定性乃是该座泵闸枢纽安全运营的关键。为此,工程部门讨论结合泵闸上部结构特征,对闸站开展组合荷载下静力特征及地震响应分析。

2.2 建模研究

根据扬州泵闸枢纽改建设计,从桩土-上部结构组合荷载作用下,考虑单孔闸室静、动力响应特征,图1（a）为采用有限元仿真平台建立的计算模型。该模型包括了地基桩网部分、上部结构以及闸墩,桩网部分共有45 根灌注桩,间距为1.5 m,上部结构中闸室宽度为2.65 m×1.8 m,根据结构材料类型,选择SOLID45、65 单元网格进行有限元划分,具有三自由度方向变形特征,全模型共获得微单元网格56368 个,节点数48628 个。模型中X～Z 分别设定有古运河河道横向、运河水流方向以及结构自重方向,模型影响范围分别取上、下游30 m,深度取40 m。考虑桩土接触面特征,闸站底部桩土接触模型见图1（b）。

图1 结构三维计算模型

为解决桩土接触面上耦合关系,引入粘弹性边界理论,图2 为粘弹性边界条件示意[9-10]。

图2 粘弹性边界条件示意

在仿真平台中对扬州闸计算模型地基边界设定为COMBIN14 单元,指代特定粘弹性边界,图3 即为地震动输入下的扬州泵闸有限元模型。计算模型中地基土体为砂砾土,其物理力学参数均按照室内土工试验结果取值。本文选取的地震波类型分别为南京波、Taft 地震波以及人工合成拟合地震波,限于篇幅,本文仅给出前20 s 加速度时程特征曲线,见图4。

图3 扬州泵闸计算模型

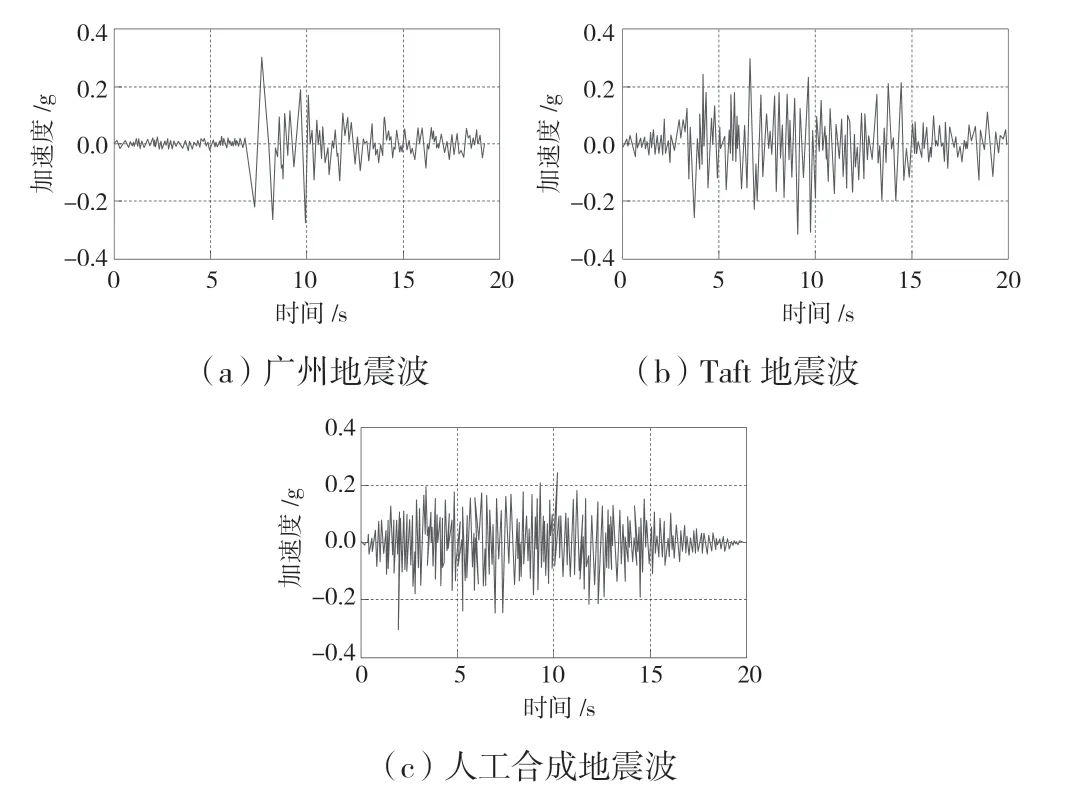
图4 加速度时程特征

仿真计算包括有静力特征与动力响应两大部分,前者静力特征计算包括有三个研究工况,分别为无水工况（A 方案,仅有结构自重）、闸前水位4.8 m（B 方案）、闸前水位5.3 m（C 方案）工况；后者动力响应特征包括有自振特性与不同类型地震波下地震响应特征分析。

3 闸站桩土-上部结构组合荷载下静力特征

3.1 位移特征

根据对闸站三个工况下静力特征计算,获得了闸室结构整体变形与各向变形特征,图5 为闸站整体位移与Z 向位移分布特征。分析可知,随着闸前水位逐步逼近洪水位,整体变形最大值均有提升,且整体最大位移发生区域并未发生较大改变。相比之下,Z 向沉降位移高于X、Y 向,在无水工况下Z 向沉降位移值达1.211 mm,而X、Y 向位移最大值较之分别减少了68.5%、81%；当闸前水位为4.8 m 时,X、Y 向位移分别为0.7 mm、0.42 mm,与Z 向位移相比,分别减少了43.4%、69.1%；同样,在闸前水位5.3 m 下,X、Y 向最大位移较之Z 向下分别有差幅31.4%、64.8%。由此可知,闸前水位愈大,则X、Y 向位移与Z 向位移间差幅愈低,闸室结构位移特征各向异性缩小。

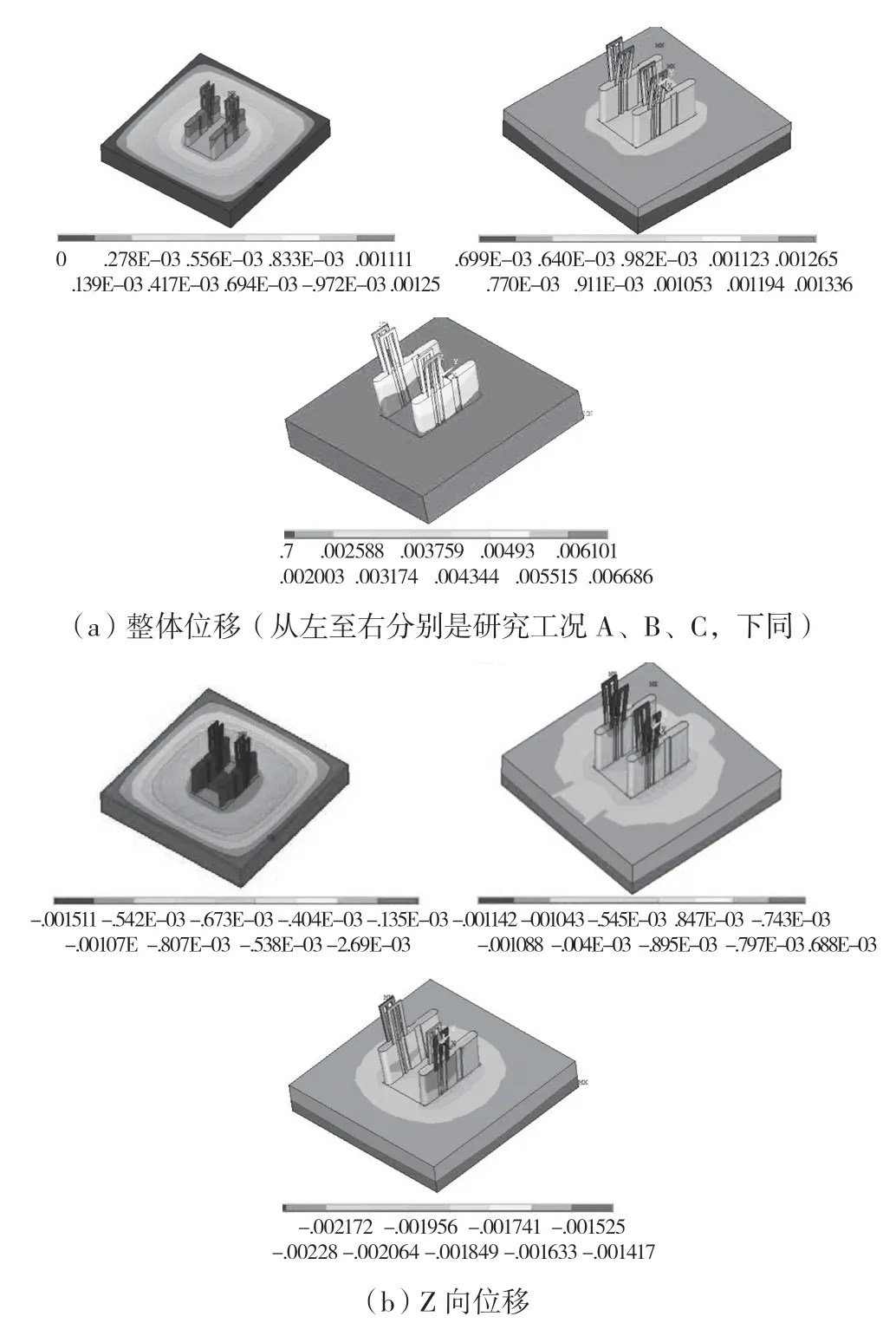
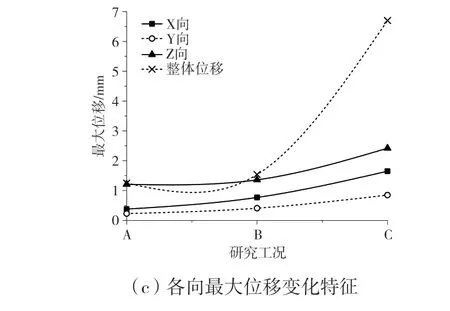
图5 各工况位移分布及变化特征

从Z 向位移分布与变化可知,有水工况下Z 向位移高于无水工况,闸前水位5.3 m 下Z 向最大位移达2.42 mm。在考虑桩土与上部结构组合荷载下,闸室桩端沉降较小,而桩顶土体沉降较大,桩身周围土体受剪应力集中效应影响,极易出现桩间土不均匀沉降。结合闸站安全设计要求,不论是有水工况下闸前水位5.3 m 或是无水工况,Z 向沉降位移最大值均未超过50 mm,满足安全设计要求[3,11]。

3.2 应力特征

同理,根据静力特征计算获得各工况下闸室结构主应力分布变化特征,见图6。由图中可知,随着闸前水位增大,闸室结构第一、第三主应力增大,闸前水位4.8 m、5.3 m 下第一主应力最大值较无水工况下分别增大了80.4%、141.3%,而在第三主应力对比下,前两者与后者工况下差幅分别为61.8%、115.1%。无水工况中张拉应力的产生仅局限在闸门面板部分区域,最大值为0.02 MPa,但闸前水位增大至4.8 m后,在该部分存在张拉区域有所扩大,拉应力可达0.03 MPa。从最大拉应力的发展来看,闸前水位4.8 m、5.3 m 下最大拉应力分布在排架与闸墩接触面上,由于桩顶土与桩端不均匀沉降造成的局部弯矩,因而产生了张拉应力分布。分析表明,控制闸前水位,有助于限制桩顶土、桩间土各向异性,进而平衡拉、压应力分布场,有效保护水工设施运营[4,12]。

图6 主应力分布变化特征

4 流固耦合下闸站地震动响应特征

4.1 自振特性

根据对不同阶次下自振计算,获得了无水工况与闸前水位4.8 m 工况下各阶自振频率变化特征,也获得了典型阶次下闸室结构振型演化特征,见图7。

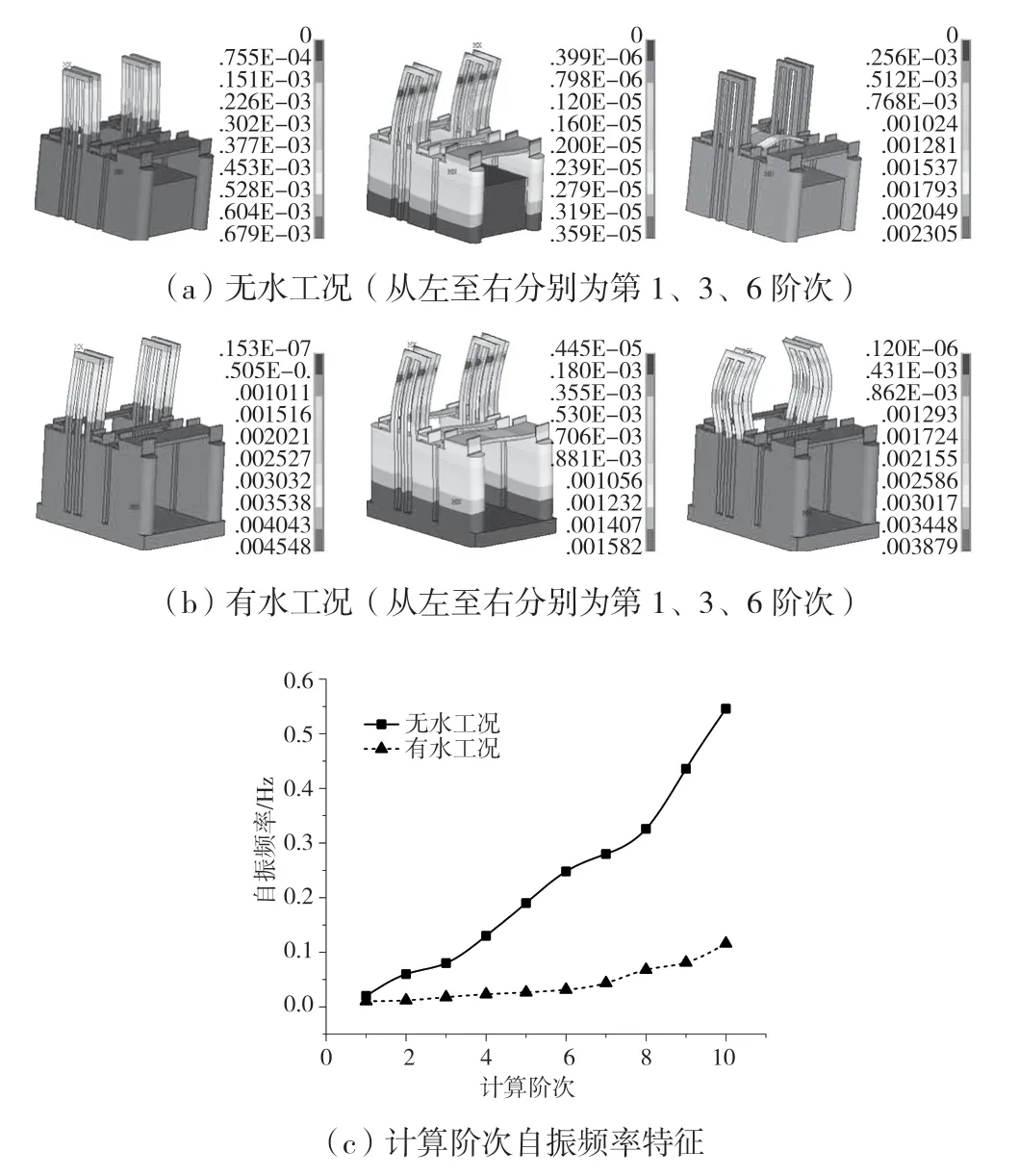
图7 闸站结构自振特性

由图中自振频率变化可知,无水方案自振频率高于有水,在第2 阶次下两者差幅为80%,而在第4、6、8 阶次下差幅分别可达82.2%、87.3%、89.2%,即随计算阶次增大,两者自振特性差幅更大[7,13]。不仅如此,从自振振型分布演化来看,当计算阶次还较低时,如第1、2 阶次下,两工况中振型均以X 向振动为主,但第二阶次下为正X 向振动特征；当计算阶次逐步延伸,第3 阶次下为反对称振型,而在第6 阶次下分别为Z 向振动、对称式振动。由此可知,有、无水工况下自振振型在初级阶次下具有一致性,当计算阶次深入发展时,振型演化特征逐步出现差异。

4.2 动力响应特征

从闸室桩端至闸顶,均测算结构动力响应特征,获得闸体、桩网以及桩土动力响应值变化特征。为有效反映闸室在桩土-上部结合组合荷载下动力响应特征,本文探讨无水工况、闸前水位4.8 m 方案下结构响应特征,图8 为两工况下三种不同类型地震波输入时,结构桩端至闸顶各断面上最大加速度响应特征[5,14]。

图8 泵闸枢纽加速度响应水平

依据图中加速度响应变化可知,不论是有水或无水工况,均为南京波输入方案下结构加速度响应特征水平最高,如在有水工况中,桩身6 m 处南京波输入下加速度响应值为0.83 m/s2,而Taft 地震波、人工合成地震波下同桩身位置处的加速度响应值分别为0.47 m/s2、0.18 m/s2；而高度延伸至上部结构后,在闸体38 m 处,Taft 地震波、人工合成地震波加速度响应值分别为0.66 m/s2、0.31 m/s2,南京波输入下较前者分别增大了1.36 倍、3.94 倍。当闸体愈靠近结构顶部,则三种地震波输入下的动力响应特征水平差幅愈显著[15]。

相比之下,无论是何种类型地震波输入下,无水工况中动力响应加速度低于有水工况,同为桩身10 m 处,无水工况中Taft 地震波下加速度响应值为0.36 m/s2,而有水工况下同类型荷载同位置处响应值较前者增大了29.6%,特别的当所在位置位于上部结构42 m 处,有、无水工况下该类型地震波方案响应值差距达32.3%。分析认为,当地震荷载,水体的存在,会增加结构惯性力作用[9],从而导致有水工况下结构加速度响应水平高于无水工况下。

5 结论

（1）闸前水位愈高,闸站结构整体变形增大,但整体最大变形所处区域并无较大改变；Z 向沉降位移高于X、Y 向,且闸前水位愈大,Z 向沉降位移较之X、Y 向差距更小；有水工况下位移高于无水工况,但两工况下位移最大值均满足安全设计要求。

（2）拉应力分布在排架与闸墩接触面上,且有水工况写张拉应力分布区高于无水工况下,第一、第三主应力随闸前水位增大。

（3）水体惯性力存在有助于削弱结构自振特性；在初级阶次下水体惯性力对振型影响较弱,随计算阶次发展,振型演化逐步出现差异。

（4）南京波输入下加速度响应水平最高,当愈靠近上部结构,不同类型地震波输入下加速度响应水平差幅加大；任一种地震波输入下均是有水工况中加速度响应水平最大。