New correlations for evaluating the equivalent bare charge mass for a cased charge
Long-kui Chen, Sheng-hong Huang, Hong-jin Chen, He-ming Wen
CAS Key Laboratory of Mechanical Behavior and Design of Materials, Department of Modern Mechanics, University of Science and Technology of China,Hefei, 230026, China
Keywords:Cased charge Energy conservation Equivalent bare charge Fracture strain Polytropic exponent
ABSTRACT Munitions contain casings that consume explosive energy.The blast load (e.g., peak overpressure and maximum impulse)intensity generated by ammunition explosion will be lower than that generated by a bare charge with equal mass.To evaluate the blast load of a cased charge under different conditions,the equivalent bare mass needs to be calculated.However, the accuracy of existing correlations strongly depends on the empirical determination of relevant controlling parameters and lacks theoretical clarification.In this paper, new correlations are proposed based on a more rigorous theoretical derivation,considering both the mechanical behaviors of the casing’s material and the change of the polytropic exponent during the expansion process of the explosion products.The controlling parameters are attributed to the rupture radius ratio and the polytropic exponent of detonation products expansion to casing rupture state.The reasonability is validated by both comprehensive numerical simulations with dynamic mechanical constitutive model and theoretical derivations.The results calculated by the new correlation show better agreement with the experimental results than those calculated by previous correlations, and the results difference is explained in more consistency with the thermos-physical properties of the charge and mechanical behaviors of casing material.Furthermore, the correlation of the cased-to-bare impulse ratio is also theoretically improved, providing a more accurate theoretical basis for both the equivalent bare mass and impulse evaluation for a cased charge.
1.Introduction
The power of an explosive blast mainly depends on the peak value of overpressure, specific impulse and time of positive pressure.To evaluate the damage effects of a blast on the target structure,UFC 3-340-02[1]and other guidance manuals were utilized to estimate the blast load.In addition,the empirical formula proposed by Kingery and Bulmash[2]was selected as the theoretical basis for the calculation of blast load.The above two evaluation methods are widely applied for the rapid evaluation of a bare charge with a certain TNT equivalent.However, in practical situations, some commonly employed structural charges are usually covered with a metal casing of a certain thickness, especially for charge warhead.For a charge with a metal casing,the detonation products drive the casing to radially expand after detonation.When the casing expands to a certain extent, cracks occur on the outer surface and then expand to the inner surface.The detonation product escapes from the crack and drives the ambient air to form a shock wave[3].During the expansion of the casing driven by the internal detonation,the casing is continuously deformed and accelerated,and the explosion energy is converted into kinetic energy of the casing.When the casing is broken, high-velocity fragments are generated and scattered into the surrounding air[4-6].Hence,the energy for generating shock waves is much less than that of the equal mass bare charge without casing.Relevant experimental studies confirmed such effects[3,7,8].It is important to accurately evaluate the blast load of cased charges.

Abbreviation A Material constant (GPa)As Constitutive parameter (MPa)At Constitutive parameter (MPa)B Material constant (GPa)B1 Constitutive parameter B2 Constitutive parameter B3 Constitutive parameter B4 Constitutive parameter Bs Constitutive parameter (MPa)Bt Constitutive parameter (MPa)By Constitutive parameter C0 Constant C1 Constant C2 Constant C3 Constant C4 Constant C5 Constant C6 Constant D Detonation velocity(m/s)DIF Dynamic increase factor DIFx Dynamic increase factor at specific plastic strain E Energy per unit volume (GPa)E0 Total energy of explosive (J)Ee Internal energy of detonation products (J)Eg Kinetic energy of detonation products (J)EG Kinetic energy of fragments (J)ES Casing deformation energy (J)f Modelling parameter H Constant coefficient I1 First invariant of the stress tensor(MPa)Ic Blast impluse with casing (kPa∙ms)Ie Blast impluse without casing (kPa∙ms)J2 Second invariants of the deviatoric stress tensor(MPa2)J3 Third invariants of the deviatoric stress tensor(MPa2)K Slope of EOS curve l Length of the casing (cm)m1 Constitutive parameter m2 Constitutive parameter Mb Equivalent bare mass (kg)Mc Casing mass (kg)Me Charge mass (kg)n Polytropic exponent n0 Initial polytropic exponent nf Polytropic exponent when casing fracture nk Polytropic exponent of final state ns Constitutive parameter nt Constitutive parameter N Constant coefficient p Pressure(GPa)p0 Initial pressure(GPa)pcj C-J detonation pressure (GPa)pf Detonation product pressure when casing fracture(GPa)pk Pressure of final state (GPa)P0 Detonation pressure(GPa)Qv Explosion heat(J/kg)r Radius (cm)r0 Charge radius (cm)rf Casing inner radius in fractured state (cm)R Gas constant (J∙K-1∙mol-1)R0 Initial casing inner radius(cm)R1 Material constant R2 Material constant Rf Casing outer radius in fractured state (cm)S Constitutive parameter t Time (μs)T Temperature (K)Tm Melting point (K)Troom Room temperature(K)T* Nondimensional temperature V Specific volume (m3/kg)V0 Initial specific volume(m3/kg)Vf Specific volume in fractured state (m3/kg)Vi Specific volume of the intermediate state (m3/kg)Vk Specific volume of final state (m3/kg)Ws Constitutive parameter Wy Constitutive parameter Y Constant coefficient Z Constant α Modelling parameter β Modelling parameter ε Plastic strain εf Failure strain εx Specific plastic strain ˙ε Strain rate (s-1)˙ε0 Reference strain rate (s-1)˙εquasi Quasi-static strain rate (s-1)η Stress triaxiality θ Lode angle (rad)λ Dimensionless ratio v Velocity (m/s)v0 Fragment velocity (m/s)v Velocity (m/s)v0 Fragment velocity (m/s)ξ Lode parameter ρ Density (kg/m3)ρ0 Initial density (kg/m3)σ1 Principal stress(MPa)σ2 Principal stress(MPa)σ3 Principal stress(MPa)σeq Equivalent yield stress(MPa)σm Mean stress(MPa)σshear Shear strength (MPa)σtensi Tensile strength (MPa)σy Yield strength(MPa)σ Equivalent stress (MPa)τ Coefficient υ Relative volume υi Relative volume of the intermediate state ψ Intermediate variable ω Material constant Subscripts f Fracture state i Intermediate state point k Final state point
Theoretically, the magnitude of the blast load of the cased charge depends on the energy converted to a shock wave.From the perspective of energy conservation, the maximum velocity of the fragment should be known first to calculate the maximum kinetic energy obtained by the casing.As early as 1943, Gurney [9] theoretically derived the expression of the maximum fragmentation velocity of the cylindrical charge casing, which is the famous Gurney formula.The Gurney formula lays a foundation for using the energy conservation method to solve the equivalent bare mass of the cased charge.Fano [7] continued to follow Gurney's relevant assumptions and suggested that the velocity of detonation products was linearly distributed along the radial direction at the critical rupture moment of the casing, that the velocity at the center of charge was zero, and that the velocity of detonation products adherent to the casing was equal to the velocity of the casing.According to the energy conservation equation,the expression of the ratio of the equivalent bare mass Mbto the charge mass Mein the cased charge was deduced as
where Mcis the casing mass and α is a constant determined by experimental data,and the term(1-α)is a factor“to account for the fraction of the total detonation energy belonging to the gases and the case as kinetic energy at time of rupture of the case”[7].Gurney found that α was around 0.2[7],but that value was revised to 0.6 by other scholars[8].Different from Fano's hypothesis on the velocity distribution of detonation products, Fisher [7] suggested that the velocity of detonation products was consistent and equal to the velocity of the casing when it was broken.Based on this hypothesis,Fisher's formula was obtained as
where β is similarly empirically determined by experiments,and its initial value and revised value are 0.2 and 0.6, respectively.In addition to the above two methods to solve the equivalent bare mass based on energy conservation,Hutchinson[10]derived a new expression of the ratio of equivalent bare mass Mbto charge mass Meby momentum conservation.
The above calculation formula Eqs.(1)-(3)show that the Mb/Meratio is only related to the mass ratio Mc/Me.Considering the relatively large validation discrepancy in Eq.(1) and Eq.(2) between calculation results and experimental data, Crowley [11] further included the influence of the explosive type and casing material and then proposed a semi-theoretical and semi-empirical formula for the Mc/Meratio.Subsequently, Hutchinson [10] derived a formula for the Mb/Meratio, including the material mechanical parameter term f based on Crowley's approach.
where f = [1-4.63(σy/P0)2/3]0.5, σyis the yield strength of the metal casing, and P0is the detonation pressure of the explosive detonation product.However, to agree with the experimental results of Dunnett[8]et al.,the value of the yield stress of steel must be adjusted for most cases (sometimes nearly 70% of its original values).This difference has not been fundamentally explained.In addition, the numerical simulations of the blast impulse of cased charges conducted by Grisaro et al.[12] showed that the yield strength and plastic strain of the casing only affect the blast impulse of the cased charge within 1%, which contradicts Hutchinson’s inferences[10,13-15].
In summary,the influencing factors for the evaluation accuracy of the equivalent bare mass of a cased charge are still unclear and controversial.To resolve these problems, this paper theoretically re-examines the expression of the ratio of the equivalent bare mass Mbto the charge mass Meof the cased charge based on the energy conservation method.Different from existing works, a new expression in consideration of both casing rupture and the polytropic process of explosive product expansion was derived.The critical rupture radius ratio and polytropic exponent of detonation products related closely with detonation expansion process were chosen as controlling parameters in the new correlation, and the corresponding theoretical evaluation formulas were derived for them.A series of numerical simulations, including explosion and metal casing rupture processes, were conducted to capture the critical rupture radius, which was well validated with both the available experimental datasets in the open literature.The consistency of the experimental data, numerical results and theoretical formula predictions were examined and justified.Based on the new expression, the expression of the relationship between the casedto-bare impulse ratio and the ratio of equivalent bare mass to the charge mass was also derived and verified.The evaluation accuracy of the blast impulse of the cased charge is also accordingly improved.
2.Theoretical derivation
To evaluate the explosion field of a cylindrical cased charge,the problem is simplified as follows: It is assumed that (1) the detonation process is instantaneously completed; (2) the casing wall thickness is constant; and (3) the broken fragments of the casing have the same velocity magnitude.According to the energy conservation of the system[11],the following equation is established:
where E0= MeQvrepresents the total energy released by the explosive of mass Me, and Qvis the explosion heat.EGis the total kinetic energy of fragments, Egis the kinetic energy of detonation products,and Eeis the internal energy of detonation products.ESis the energy consumed by casing deformation and crushing, accounting for 1-3% [16].Considering that the energy ratio of deformation energy is very small (<5%), and referring to the practices of other studies in similar situations [10,13-16], we ignore it here.After disregarding the energy of casing deformation and breakage,Eq.(5) can be rewritten as
Selecting the critical rupture state of the casing as the research object, the kinetic energy of the casing is
where v0is the fragment velocity when the casing is broken.
As shown in Fig.1,for the cylindrical cased charge with length l,the initial radius of charge is r0.After charge initiation,the radius of the casing expands from r0to r, the volume of the detonation products increases from V0to V,and the velocity of the detonation product at radius r is v.Assuming that the length l of the casing remains unchanged,the kinetic energy of the detonation products in the expansion process can be expressed as
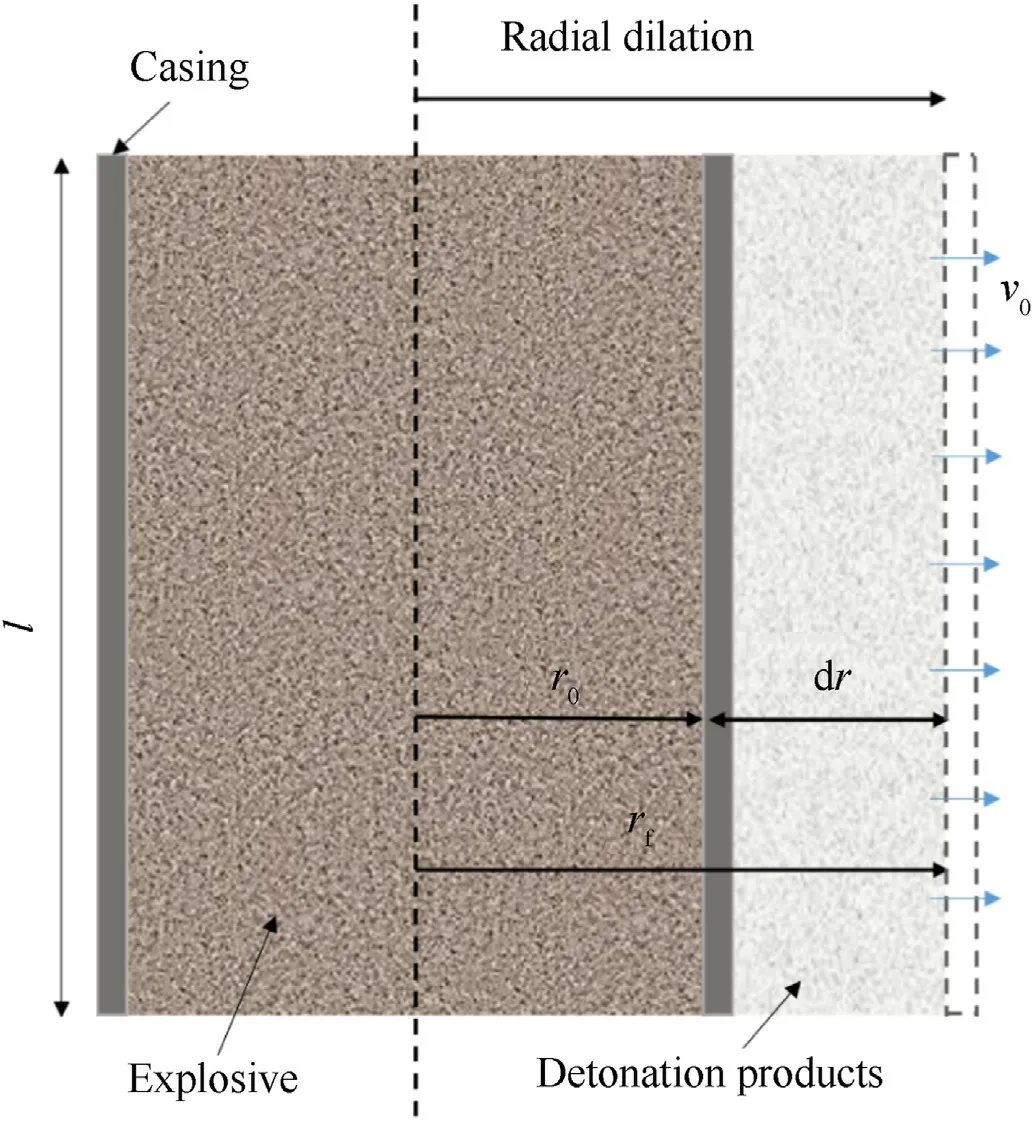
Fig.1.Schematic of the expansion process of a cylindrical cased charge.

According to the work of Fisher[7]and Gurney[9],it is assumed that velocity v of the detonation products linearly increases along radial r from 0 to v0and that the density is uniform.The radial velocity v of the detonation products has the following relationship with velocity v0when the casing expands to the critical rupture radius rf.

The internal energy of the detonation products corresponding to the critical rupture state of the casing can be accounted for as the work performed by the detonation products expanding from volume Vfat the time of the rupture to infinity, denoted as
The expansion process of the explosive detonation product is a polytropic process.According to Ref.[16],the polytropic exponent n rapidly changes from approximately 3 to the range of 1.5-1.7 from the initial state of the casing to the rupture state of the casing and then gradually decreases to the range of approximately 1.2-1.4 in the subsequent process.By the polytropic process equation pVn=Z, the pressure p of the detonation products can be expressed as p = ZV-n, where Z is constant, and the internal energy Eeof the detonation products can be obtained by substituting it into Eq.(12).
where pfis the pressure of detonation products when the casing begins to rupture.The polytropic process of detonation product from the initial pressure p0to pfis discretized into k(k →∞)subtle change processes obeying the isentropic equation
The pressure relationship for each subtle change process is as follows
After multiplying the left and right of Eq.(15) respectively, we get
Let n1- n0= n2- n1= …nk-1- nk-2= Δn, Δn<0,|Δn|→0;∀k→∞,υi= Vi/V0,ψ becomes


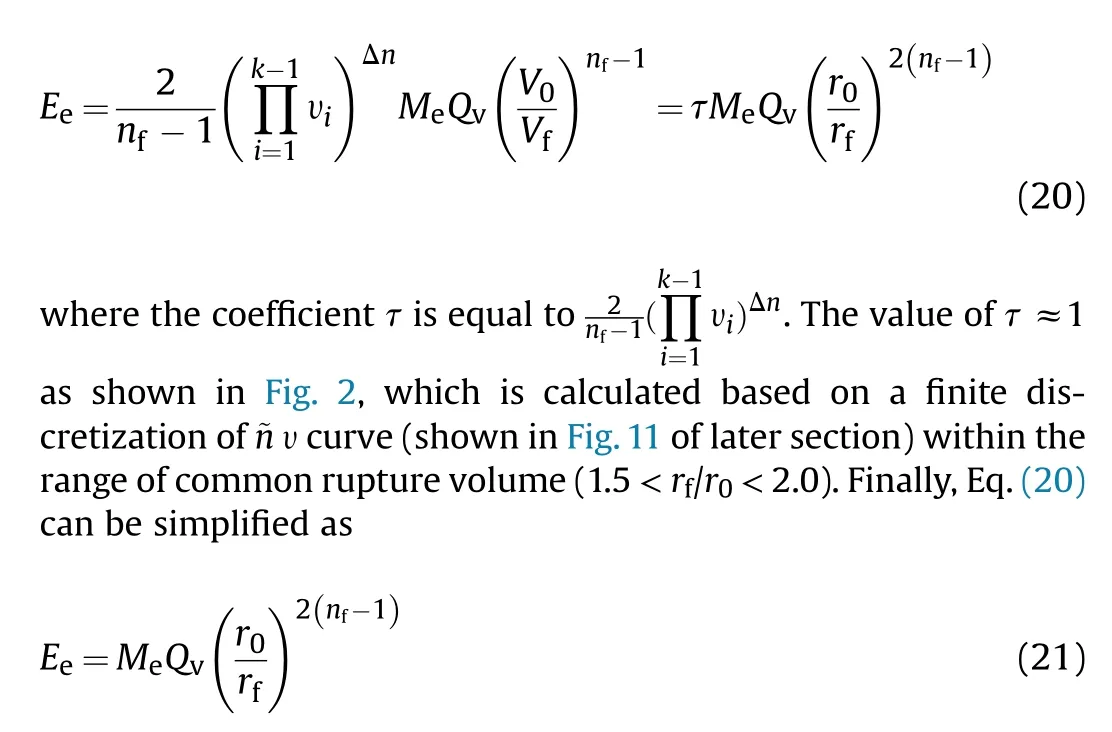
Substituting Eqs.(7),(11)and(21)into Eq.(6),the square of the velocity v0of the fragment is

More Detailed derivation of Eq.(22)and Eq.(23)could be found in Appendix A.
Fig.2.Variation of coefficient τ with relative volume υ.
According to Eq.(23),the ratio of the equivalent bare mass to the charge mass of the cased charge is related to three controlling parameters,namely,the mass ratio Mc/Me,casing rupture radius ratio rf/r0and polytropic exponent nfof detonation products.The first parameter Mc/Meis commonly presented in previous correlations,while the latter two are new parameters.The casing rupture radius ratio rf/r0is directly related to the ductility of its material properties.Under the action of detonation products,the casing with better ductility will expand to a larger radius during rupture, and vice versa.The value of the polytropic exponent nfis related to both the explosive type and preliminary expansion stage.For a cased charge,Mc/Meis a known quantity,while the casing rupture radius ratio rf/r0and the polytropic exponent nfof detonation products need to be determined by the explosion process.
3.Determination of the rupture radius ratio
There are several ways to determine the rupture radius ratio.The first way is measurement through experiments, which can usually be accomplished with a high-speed photography technique.However, few results of high-speed photography have been published, including the work of Dunnet [8].In terms of fracture mechanics,the magnitude of the rupture radius is closely related to the fracture strain during expansion of the casing.Hutchinson[13]also concluded that the radius ratio could be estimated using fracture strain; however, he did not give further evaluation details.The relationship between the critical fracture strain of the casing material and the rupture radius ratio can be analyzed in a twodimensional deduction based on some simplifications.
Due to the axial strain is far less than and circumferential strain,the deformation process of the cylinder metal casing can be simplified to a two-dimensional ring [17].The radius of the initial state of the casing and that of the critical rupture state of the casing are shown in Fig.3.Assume that the critical fracture strain of the material when the casing ruptures is denoted as εf.The following relationship is established according to the equal areas (shades of gray) of the two rings.
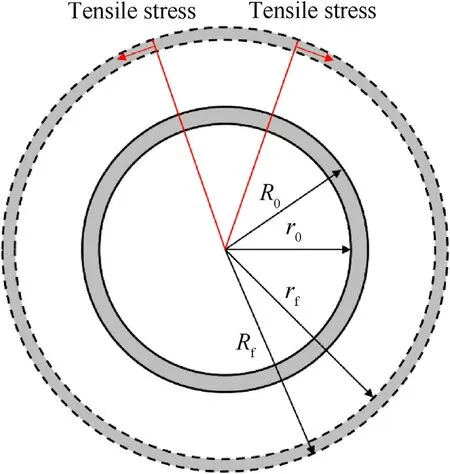
Fig.3.Expansion of the 2D ring casing from the initial state to the critical rupture state.
When the casing is close to fracture, its circumference will attain the ultimate deformation strain limit of tension (1+ εf) with expansion of explosive products.The circumference relation of the casing in the two states can be expressed as follows:
Combining Eq.(24) and Eq.(25) and letting λ be Rf/rf, the expression of the rupture radius ratio rf/r0can be obtained as
The detailed derivation of Eq.(26)could be found in Appendix B.According to Eq.(26), it is interesting to find that in the critical rupture state, λ is close to 1 after maximum tension deformation due to expansion for most casing materials,and the radius ratio rf/r0can be calculated as
It is truly a simple correlation to evaluate rf/r0.Here,it should be noted that Eqs.(26) and (27) explain the experimental results of Refs.[13,16], in which the variation in the initial casing thickness has little effect on the critical rupture radius ratio in conventional designs.However, εfis a function of parameters such as the stress triaxiality, Lode parameter, etc, in other words, it is a parameter related with fracture process.Measurements of εfbased on conventional mechanical tests may not be fully in accordance with those in practical explosion loading states.Therefore, we try to conduct 3D numerical simulations to evaluate the rupture radius ratio of the casing, in which material constitutive equations in consideration of dynamic mechanical parameters such as the stress triaxiality, Lode parameter, etc.are used to promote its prediction accuracy.
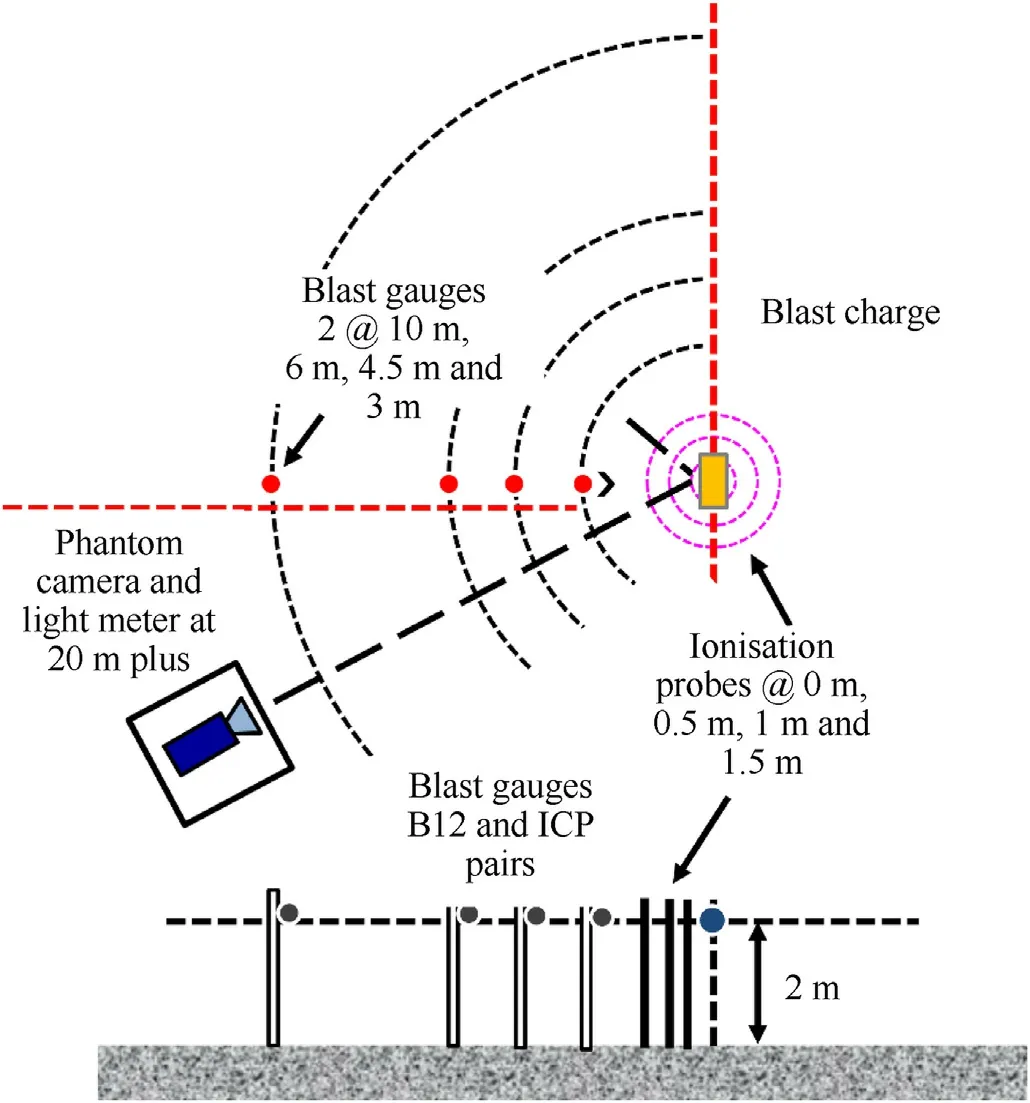
Fig.4.Experimental setups reported by Dunnet [8].
The experimental cases conducted by Dunnet [8] are used as testing case of numerical simulations.The experimental setups by Dunnet [8] are shown in Fig.4 for convenience of analysis.
In the experiments, several blast measuring points were arranged flush with the charge center to record the pressure-time histories.The type of explosive chosen is RX1100 (88wt% RDX and 12wt% plasticiser/binder).The charge mass is 1 kg; the mass ratio Mc/Meranges from 0.5 to 10; the charge shape is cylindrical;and the length-diameter ratio is 2:1.Steel EN24 and aluminum alloy 6086T6 are two different casing materials utilized in experiments.The experimental cases apply the combination of different explosives and different casing materials.The maximum impulse value was obtained by integrating the pressure-time histories at each measuring point, and the equivalent bare charge mass Mbto charge mass Mewas obtained by transforming the scaled impulse at different scaled distances from the standard 1 kg TNT explosive.
The numerical simulations focused on the expansion and rupture process of different casing materials driven by detonation.Nonlinear finite element analysis software LS-DYNA was selected for calculation [18].The multi-material arbitrary Lagrange Euler(MM-ALE) method was employed to accurately capture shock waves and to describe material flows [19,20].The computational domain consists of a fluid domain and solid domain.The fluid domain is composed of explosive and air, which are connected by common nodes.The solid domain is a casing with a certain thickness covering the explosive.The grids of the fluid domain and solid domain are separately divided;the explosive and air are divided by Arbitrary Lagrangian-Eulerian (ALE) elements; and the casing is a Lagrange element.The fluid-structure interaction(FSI)algorithm is adopted to realize the transfer of force between the fluid and the solid.The explosion initiation is set at one point on the cylindrical axis near the upper head of the cased charge according to the practical explosion initiation setup.Considering the cylindrical charge shape and explosion initiation on the axis,a 1/4 symmetric 3D model is adopted in the simulation, as shown in Fig.5.The radius of the computational domain is 0.25 m, and the height is 0.5 m.According to the suggestions of relevant literature[12,21,22],the casing is meshed with 0.001 m elements, and the explosive is meshed with elements smaller than that of the casing to achieve good coupling effects.The fluid domain is meshed with elements both adaptive to fine boundary of adjacent casing elements and to 0.005 m far field boundary elements of the computational domain.The total amount of the meshed elements ranges from 2.3 million to 2.7 million according to different thickness of the casing.The outer boundary is set as a non-reflection boundary.
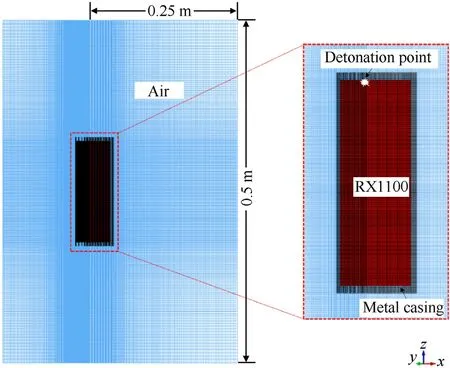
Fig.5.1/4 symmetric simulation model.
The explosive used in the numerical simulation is the RX1100 explosive, whose parameters are similar to the C4 explosive [12].The material parameters of RX1100 are defined by the keyword*MAT_HIGH_EXPLOSIVE_BURN, and the Jones-Wilkins-Lee (JWL)equation of state(EoS)[23]is used to describe its pressure variation with parameters,
where A, B, R1, R2and ω are material constants, υ= ρ0/ρ is the relative volume, and E is the energy per unit volume at the initial moment.Relevant parameter values of RX1100 and JOB9003 explosives are listed in Table 1.
The air is modeled with unbiased stress hydrodynamics,and the equation of state is a polynomial that is defined as

The constitutive model proposed by Zhou and Wen [25] was used to calculate the stress of casing material under a high strain rate driven by detonation.The model expresses equivalent stress σeqas a function of equivalent plastic strain ε, lode parameter ξ,strain rate ˙ε, and dimensionless temperature T*.The formula form is as follows
where At,Bt,ntare material parameters,which can be obtained by fitting the quasi-static tensile true stress-true strain curve.γpis the ratio of shear strength σshearto tensile strength σtensi, which is defined as follows:
where As,Bs,nsare constants to be determined from the quasi-static true-stress/true-strain curve in torsion.
The Lode parameter ξ is related to the Lode angle θ on the π plane,and both satisfy ξ = - sin(3θ).The Lode angle range is - π/6≤θ ≤π/6,so the range of the Lode parameter is - 1 ≤ξ ≤1.

where DIFxis the dynamic increase factor at specific plastic strain ε = εx, which can be estimated with the following empirical expression [25-27]

where Wx,By,Wy,S are constants determined by material dynamic experiments.˙ε0is the reference strain rate,which is taken as 1 s-1,and ˙εquasiis the quasi-static strain rate,and its value is usually less than 103s-1.
The softening effect of temperature T on strength is also considered in the dynamic constitutive model of metallic materials.T* is the nondimensional temperature related to the current temperature T,which can be expressed as T*=(T -Tm)/(Tm-Troom),where Tmis the melting point of a material and Troomis the room temperature.m1and m2are material constants determined by high-temperature material mechanical tests.
Metal materials often fail under high-explosive loads.To accurately simulate the dynamic mechanical behavior of materials,it is necessary to select better failure criteria.Here we still choose the failure criterion proposed by Zhou and Wen [25], and the expression is as follows:

Table 1Material properties for explosive RX1100 [24] and JOB9003 [17].
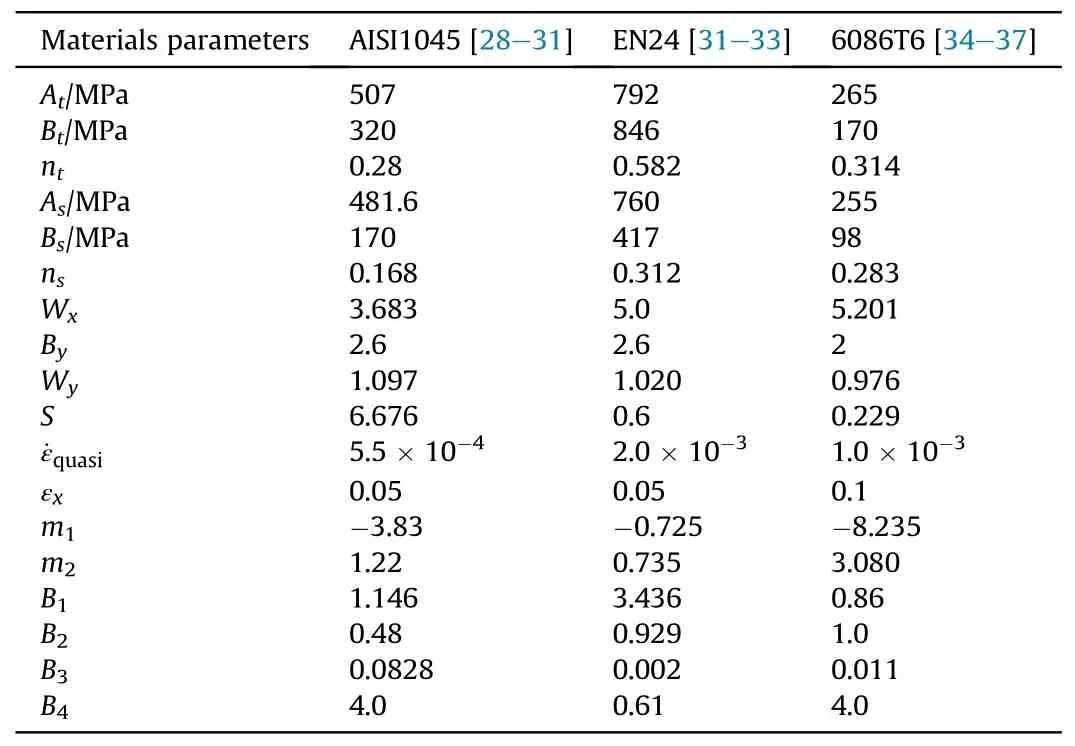
Table 2Material parameter values in constitutive models and failure criteria.

The reliability of the numerical model and method is validated with the experiment by Dong et al.[38], in which the dynamic fracture process of AISI 1045 cylindrical casing driven by detonation is recorded with high speed photography.The inner diameter of the cylindrical casing is 40 mm, and the wall thickness is 5 mm.The nominal length of the cylinder is 140 mm,and the internal charge is JOB9003 explosive.The mesh size and calculation condition settings of this case are consistent with the previous settings.During the experiment, a high-speed camera was used to record the dynamic deformation of the 1045 steel casing at different typical times.The comparison of the numerical deformation and fracture results with the experimental images at corresponding moments is shown in Fig.6.The results indicate that both the initiation position of the crack on the casing surface and the whole process of the axial cracks propagation to the end caused by the tensile action obtained by the numerical simulation are in good agreements with the experimental results.The reliability of the numerical models and methods is validated.
Here, it is worth noting that in the theoretical derivation, the velocities of the fragments are assumed to be the same due to 2D simplification.However, according to both experimental observation and numerical simulation results, it is clear that both ends of the casing are affected by sparse effects during expansion,resulting in a low fragment velocity near the casing ends [4,5,39,40], as indicated in Fig.6.The fragment velocity and thus the kinetic energy EGin theoretical models may be generally higher than those in the experimental/numerical evaluation cases.Since the total detonation energy of the explosive is constant,the higher counting of EGwill reduce the energy obtained by the air Ee.As a result,the calculated equivalent bare mass of the cased charge with the theoretical model may be lower than that with experimental/numerical evaluation.

Fig.6.Comparison of numerical simulation images(bottom)and high-speed photographic images(top)[38]of casing expansion and fracture at typical moments:(a)0 μs;(b)4 μs;(c) 6 μs; (d) 11 μs; (e) 18 μs.

Fig.7.Schematic diagram of the determination of the casing rupture radius rf in numerical simulations.
However, in our new proposed theoretical model, we use rfinstead of fragment velocity as one of the controlling parameters.As shown in Fig.6,rfin the rupture state of both the experimental test and numerical simulation is not a constant, as the theoretical model indicates, which is a bulging profile consistent with fragment velocities due to the sparse effects of the two ends.Therefore,reasonable determination of the fracture radius rfaccording to its profile may reduce the deviation between the theoretical model and experimental/numerical evaluation.Fig.7 shows a schematic diagram of the determination of the casing rupture radius rfin the numerical simulations.The red solid line is illustrated as the profile of numerical simulations when the whole casing is critically ruptured,and the volume inside the casing profile can be obtained by integrating the volume along the axial direction.Then, an equivalent standard cylinder with the same volume is calculated and illustrated as a black dashed line.The radius of the standard cylinder is chosen as the fracture radius rf.It is clear that such a kind of treatment with rfis based on the equivalent of expansion volume, which accounts for the sparse effects of two ends and therefore reduces the deviation between the theoretical model and experimental/numerical evaluation.
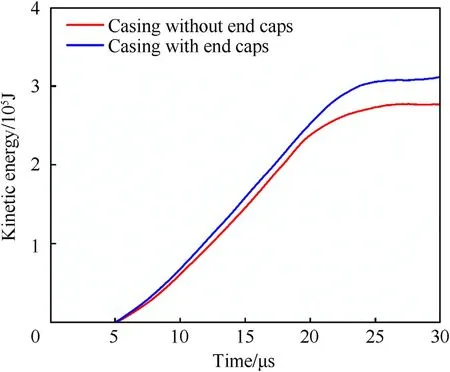
Fig.8.Comparison of kinetic energy change curves of casings with different end conditions.
Another important question invoked by the same problem of sparse effects is the end caps.Generally, the testing cased charge contains two end caps.The end caps can suppress the effects of rarefaction waves [41].Fig.8 shows the numerical results of the casing kinetic energy time-history curves of the case charge (Mc/Me= 2) with and without end caps.It can be observed from the figure that the maximum kinetic energy of the casing with the end cap (red solid line) is significantly higher than that of the casing without the end cap (blue solid line).Thus, the deviation of the equivalent bare mass of the cased charge between the theoretical model and experimental/numerical evaluation due to the sparse effects of the two ends will be further reduced due to the design of the end caps.
Fig.9 shows the expansion rupture process of the steel cased charge with Mc/Me=2 at different moments obtained by numerical simulations conducted with same methods and models.The following observations are noted:
(1) Figs.9(a)-9(c)shows the preliminary evolution process after explosion initiation.The upper end cap of the casing expands and deforms along the axial direction, while the cylindrical casing shell adjacent to the upper end cap mainly expands along the radial direction.At t=11.98 μ s,the upper end cap of the casing separates from the main casing shell due to rupture.
(2) With the propagation of explosive detonation,the cylindrical casing shell continues to expand along the radial and axial directions.The expansion radius in the upper section is larger than that in the lower section,which is consistent with the explosive detonation propagating axially from the upper end cap to the lower end cap.The upper section of the casing will initially attain the condition of rupture.The cracks formed in the upper section will continuously propagate axially to the lower section,as shown in Figs.9(d)-9(f).Due to the quicker propagating speed of the stress shock in the casing, the lower end cap separates from the main casing shell at t=24.97 μs,while the cracks propagate to the lower head of the left main casing shell at t = 29.47 μ s.At this moment, the casing is fully broken up.We define this moment as the critical rupture moment of the cased charge,as shown in Fig.9(i).After this moment, the explosion products may propagate out through cracks, and the casing will continuously be outwardly driven by explosion products.
Fig.10(a)and(b)show the corresponding critical rupture states of both the steel-cased charge and aluminum-cased charge simulated in the present investigation with different Mc/Me.Further observations are noted as follows:

Fig.9.Expansion and rupture process of the 2 kg steel casing:(a)0 μs;(b)8.00 μs;(c)11.98 μs;(d)14.48 μs;(e)17.50 μs;(f)22 μs;(g)24.97 μs;(h)26.47 μs;(i)29.47 μs;(j)36.97 μs;(k) 140.98 μs; (l)50 μs.
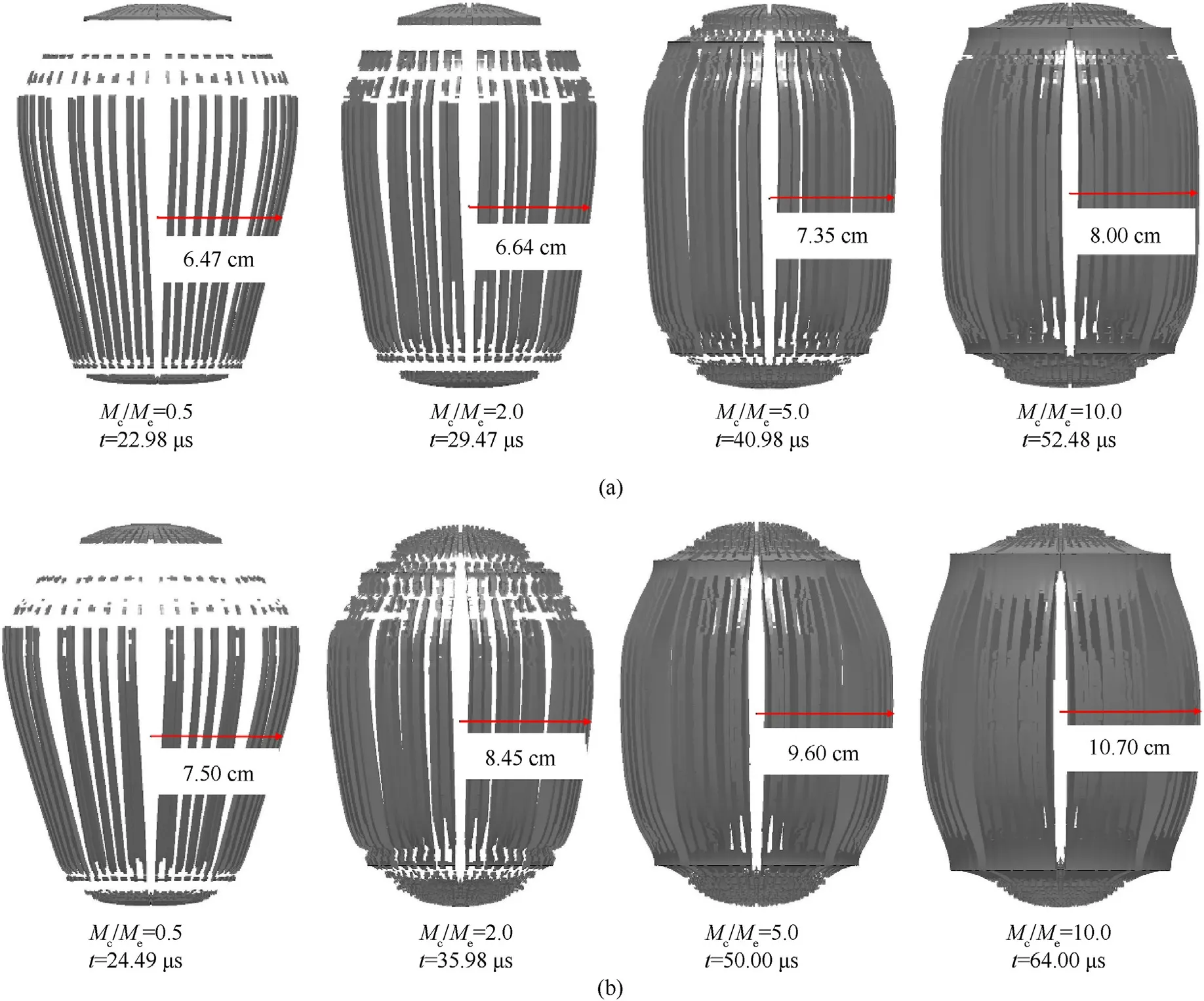
Fig.10.Deformed shape and outer radius at the critical rupture state of different casing materials: (a) EN24; (b) 6086T6.
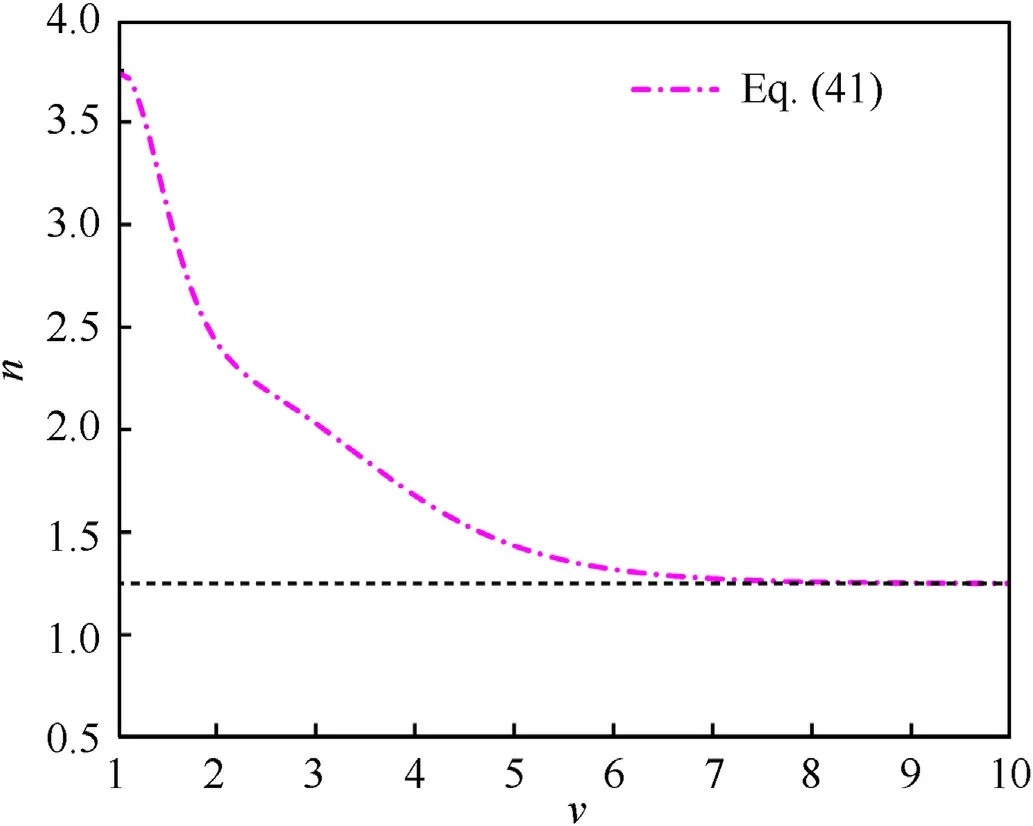
Fig.11.Variation in the polytropic exponent with the expansion of detonation products.
(1) For both cased charge series, the time to attain the critical rupture state reasonably increases with the mass ratio Mc/Mesince the casing thickness is increased.The profile shape of the casing gradually changes with different Mc/Mevalues,as shown.For the small Mc/Mecase,the whole casing,including end caps, is ruptured into fine fragments due to the small strength of the thin shell wall thickness, while for the Mc/Me≥5 cases, the casing presents better anti-shock performance due to the larger wall thickness.Notably, the casing may experience multiple shocks impacting larger wall shell thickness cases since the shock may reflect, converge to the center and resume,driving the casing to expand outward and deform as a whole until rupture.Furthermore, when the mass ratio Mc/Meis small, the end caps are easily separated from the cylindrical casing,the influence of rarefaction waves near the end caps is relatively large, and the rupture radius profiles of the casing are very different (especially for Mc/Me= 0.5).When the mass ratio Mc/Meis large, only the expansion radius of the casing near the end position is slightly lower than that of the middle section,indicating that the increase in the mass ratio Mc/Meenhances the suppression of rarefaction waves by the end caps.
(2) The geometric dimensions corresponding to all cases in Fig.10 are listed in Table 3.The results in the table show that the final critical rupture radius ratio rf/r0calculated by different mass ratios varies by case.In general,rf/r0increases only slightly with an increase in the mass ratio for the two kinds of casing materials, which verifies the rationality of ignoring the effect of wall thickness when deriving Eq.(27).Arelatively large difference between the two kinds of casing material is observed.For example,the average rf/r0of EN24 is 1.68, while that of 6086T6 is approximately 1.98, which is reasonably related to the ductility of the material since the ductility of aluminum alloy 6086T6 is larger than that of steel EN24.
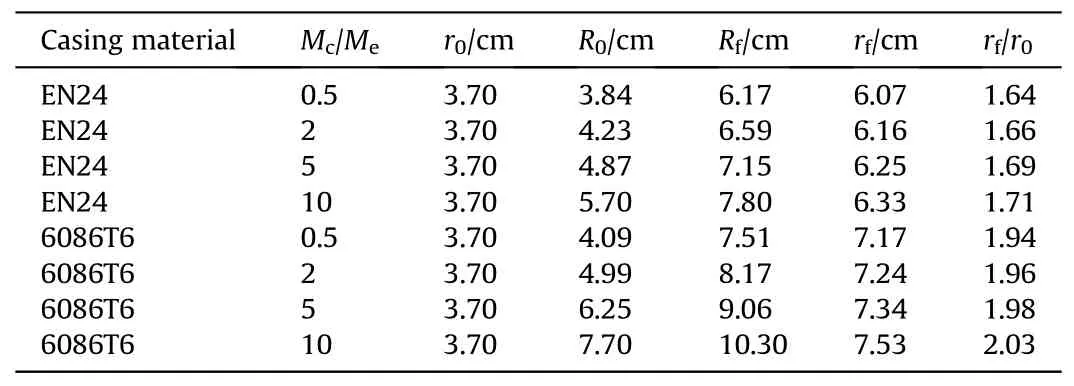
Table 3Dimensions of different cylindrical casings in the initial state and critical rupture state.

Table 4Ratio of the radius of expansion and rupture of different material casings.
By post-processing the results of the DYNA program, the effective plastic strain range of all failed elements on the inner wall of the cylinder is obtained.We use their average value as εf.Table 4 lists the comparison of critical rupture radius ratio values predicted with Eq.(27) based on average εfobtained from numerical simulations and experiments from the literatures for different kinds of casing materials.The fracture strain of mild steel in the table is uniformly replaced by that of Q235 steel in Ref.[42] for reference.The yield stress values for all materials are also included for reference,since Hutchinson[15]used yield stress to account for the effects of ductility in his correlation.It is clear that the critical radius ratio rf/r0predicted by Eq.(27) fall in range of data of reference or numerical simulations, demonstrating its rationality.As compared with data of yield stress of casing material, they obviously fail to establish such a clear relationship with rf/r0,although the data are so different for different materials.
4.Polytropic exponent
Under the condition of Chapman-Jouguet (C-J), slope K of the EoS isentrope and relative volume υ can be expressed as follows[43]:

Since the C-J detonation pressure pcjalso satisfies p =ZV-n,the calculated detonation pressure pcjis substituted into Eq.(39) and
combined with Eq.(37) and Eq.(40) to obtain n= K.However, Eq.(38)indicates that when the relative volume υ tends to infinity,the value of K ≈1.When the pressure of the detonation product is near ambient pressure, n is similar to the isentropic exponent of the explosion gas mixture.However, for different types of explosives,the polytropic exponent n of the explosion gas mixture is approximately 1 +ω [43].Therefore, we assume n ≈(1 +ω)K, i.e., the expression of the polytropic exponent n can be expressed as


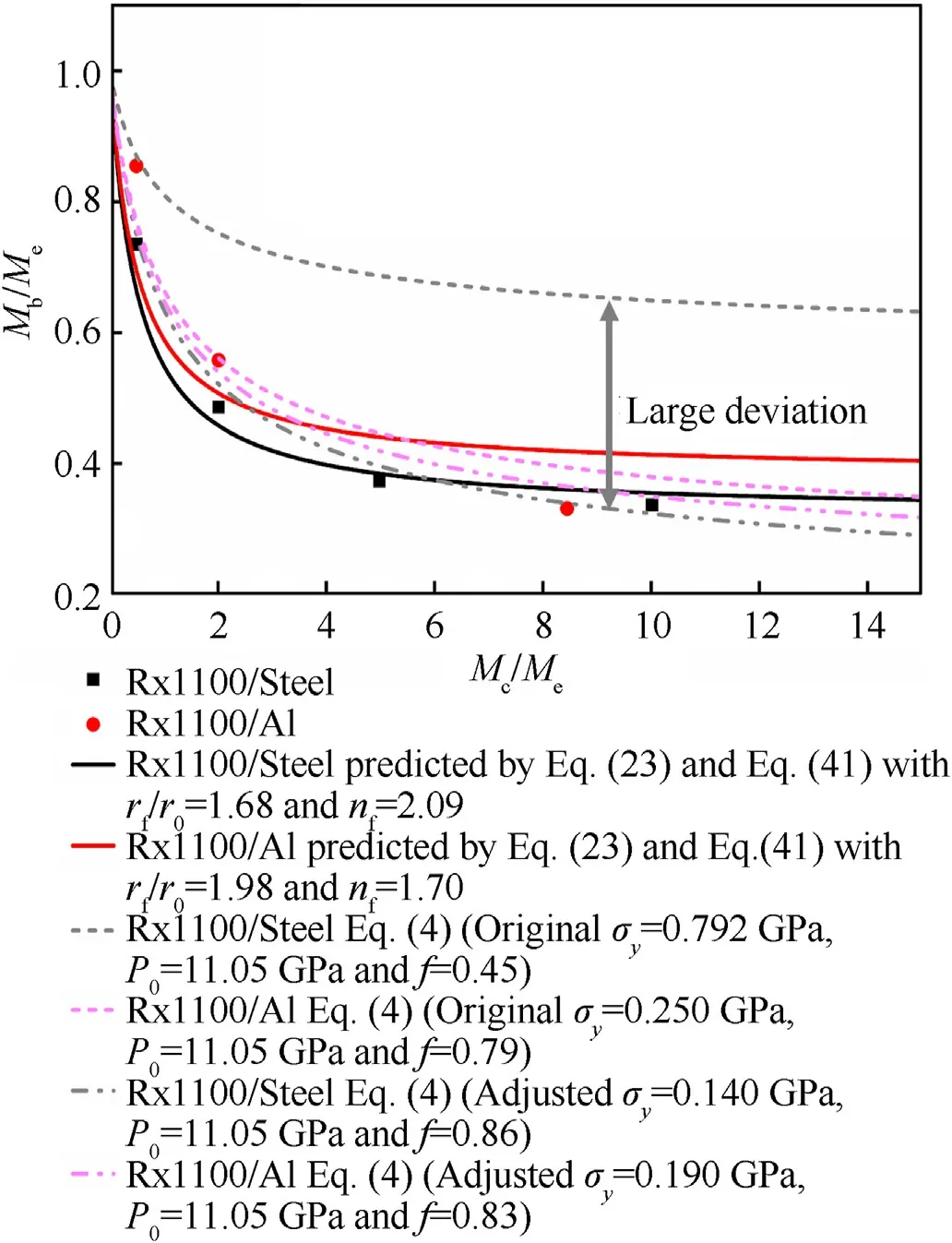
Fig.12.Comparison of the present investigation and existing correlation with the data of Dunnet et al.[8].
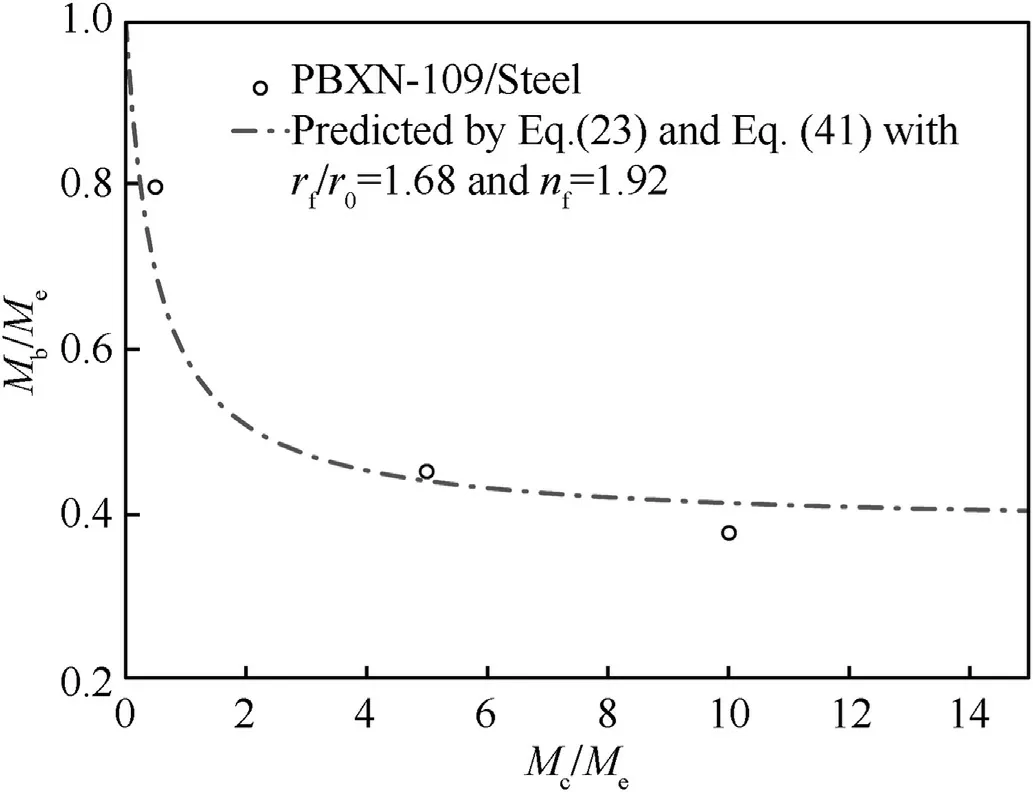
Fig.13.Comparison between the predicted results and the experimental data from Locking et al.[44].
5.Validations with experimental data
Based on the initial work of Team member Dunnet[8], Locking et al.[44]evaluated the equivalent bare mass of a series of charges cased with different masses of EN24 steel under similar experimental conditions.We summarized the three years of research results for both and compared the experimental data with the evaluation results by correlations of Eqs.(23)and(41)proposed in this paper.The results are shown in Figs.12 and 13.The discrete data points in Fig.12 are experimental values,and the solid lines are evaluated by correlations in the present investigation.The dotted lines represent the results evaluated by the existing correlation(Eq.(4)).According to the figure.
1) The results evaluated by the present correlations generally show better agreement with the experimental data than the results predicted by the existing correlation(Eq.(4))of Hutchinson[10].Note that when the mass ratio Mc/Meis small, the sparse wave has a relatively large impact on the results,which will cause the values evaluated with the theoretical model to be smaller than those with experimental tests.The data points in the 0-3 range of Mc/Meconfirm this conclusion.When the mass ratio Mc/Meis relatively large,the sparse wave effect is well suppressed by the end caps, and the results evaluated with the theoretical model are generally more consistent with the experimental results.
2) For the results of explosive RX1100 predicted by the existing correlation of Hutchinson,there is a relatively large discrepancy between the prediction and the experimental values, with the yield strength σyof EN24 steel taken as its original value of 792 MPa.However, if we adjust the yield strength σyof EN24 steel, we can reduce its discrepancy to the proper state, as indicated in Fig.12(this kind of adjustment was also adopted in Ref.[10]).However, the yield strain of steel (140 MPa) after adjustment is smaller than that of aluminum(190 MPa),which is obviously inconvincible.
3) In the process of explosion with a casing,the metal casing bears high pressure and a high strain rate of the strong shock load.Although the load magnitude reaches the yield strength, the casing will undergo the plastic hardening stage to deformation without rupture, and the casing is still in an acceleration state.Therefore, choosing the yield strength of casing material as a parameter to account for rupture effects of explosion is unsuitable.Compared with the existing correlations, choosing fracture strain as the mechanical parameter of correlation in this paper is more consistent with the mechanical and physical processes.
The correlations proposed in this paper involve the evaluation of the polytropic exponential of the detonation product in the state of casing rupture.For ideal explosives (e.g., RX1100), the detonation parameters follow the JWL equation of state, and nfcan be calculated with Eq.(41).However,for nonideal explosives,there may be certain errors since the detonation parameters deviate from JWL.In this case, for convenience of evaluation, we can approximate JWL constants for the nonideal explosives under the conditions of equivalence when the charge density and detonation velocity are known.Here, we use the engineering empirical Eq [45] to approximate them as follows:

Table 5Material properties for explosive PBXN-109.
In a supplementary experiment by Locking et al.[44],the charge was a PBXN-109 (64 wt% RDX, 20 wt% aluminum,16 wt% binder/plasticiser) explosive, and the casing was EN24.For the PBXN-109 explosive, its initial density ρ0, detonation velocity D and energy density E are provided in Ref.[46],and the material parameters of PBXN-109 calculated in combination with Eq.(42) are shown in Table 5.
Since the casing material is still EN24, we keep the rupture radius rf/r0unchanged at 1.68.The parameters in Table 5 are substituted into Eq.(41)to obtain the rupture polytropic exponent nf(1.92) at a rupture radius of 1.68, which is slightly smaller than that of RX1100(2.09)for the same expansion degree.This finding is reasonable because detonation temperature T of aluminized explosive PBXN-109 is higher than that of ideal explosive RX1100.Combining the polytropic process equation pVn=Z and the ideal gas state equation pV = RT, it can be derived that TVn-1= ZR-1.According to this relationship, the polytropic exponential n of expansion products with higher temperature T should be smaller than that of expansion products with lower temperature at the same expansion volume.
Next, the Mb/Mecurve (dashed line) of the cased PBXN-109 charge with EN24 vs.the mass ratio of Mc/Mepredicted by the correlations of Eqs.(23), (41) and (42) is shown in Fig.13.A comparison of the experimental data (discrete points) with the predicted values reveals that the two datasets show good agreement,demonstrating that the Mb/Meof nonideal explosives can also be evaluated with reasonable accuracy by the correlations proposed in this paper.
6.Solution for blast impulse ratios
To further determine the impact degree of the casing on the impulse of the blast load, the impulse ratio Ic/Iemust also be calculated.Icis the impulse produced by the cased charge,and Ieis the impulse produced by the bare charge.The impulse ratio Ic/Ieis related to the ratio Mb/Meof the cased charge, and the specific impulse ratio equation is derived as follows:

where H and Y are constants.Eq.(44)divided by Eq.(43)yields the expression of impulse ratio Ic/Ieon Mb/Meas
Grisaro [12] used Eq.(45) to fit the numerical results, and the optimal value of Y is 0.9088.Considering that Y is nearly 1, and Ref.[16] pointed out that the experimental results of the scaled impulse conform to the form of Eq.(44) with Y = 1.Hence, this paper assumes a simple linear relationship between the scaled impulse and the reciprocal of the scaled distance, that is, Y = 1.With Y = 1, Eq.(45) becomes
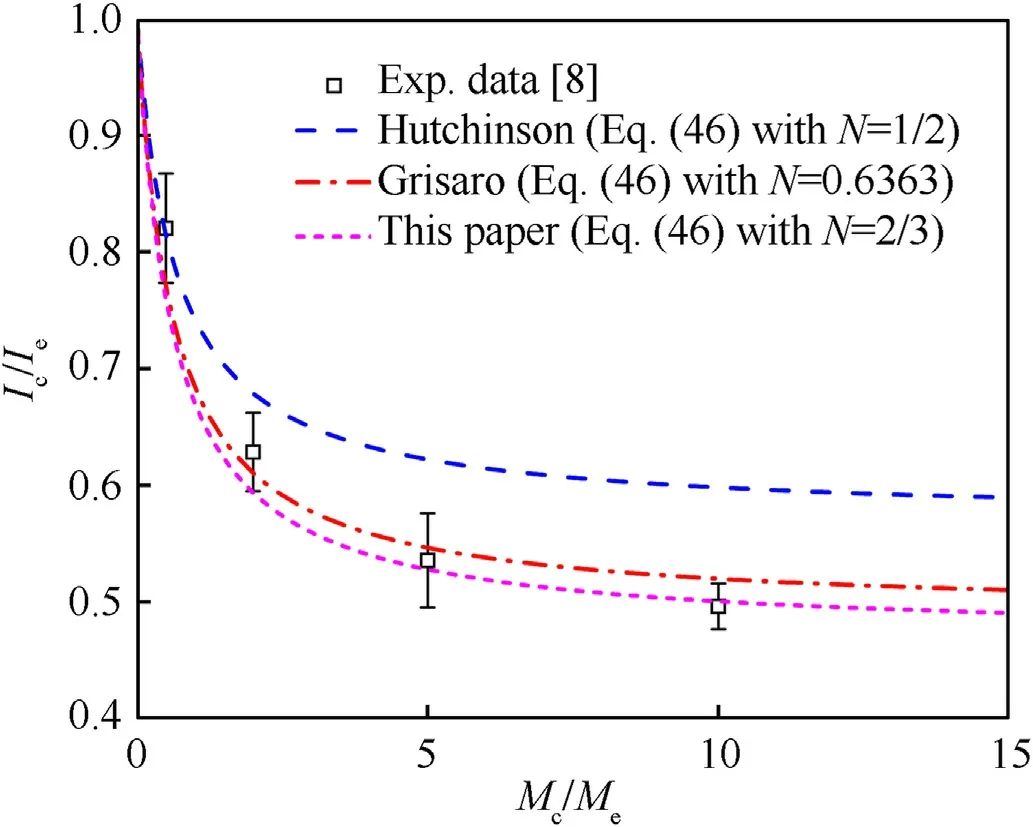
Fig.14.Calculation results of Eq.(46) with different values of power exponent N are compared with the experimental data.
Eq.(46) shows that the impulse ratios Ic/Ieand Mb/Mehave a power function relationship.The power exponent N obtained in this paper is 2/3.Different scholars hold different views on the value of the power exponent N.Here, we substitute three power exponential values into Eq.(46) and compare the calculated impulse ratio with that of the experimental results in Ref.[8].The values of the power exponentials are listed as follows:1/2 adopted by Hutchinson,0.6363 adopted by Grisaro,and 2/3 deduced in this paper.The experimental results of the impulse ratio are produced by the case charge of RX1100 with EN24.A comparison between the calculated results with different power exponents and the experimental results is shown in Fig.14.The theoretical value obtained by Hutchinson's square root method substantially deviates from the experimental results,indicating that the impulse ratio Ic/Ieand Mb/Meis not a square root relationship.The calculation results of 2/3 power in this paper are similar to the calculation results of 0.6363 power adopted by Grisaro.Both generally show agreement with the experimental results, but the results obtained by the correlations proposed in this paper show better agreement.The calculation result of N=2/3 is in good agreement with the experimental data,which also proves the rationality of the hypothesis about the linear relationship between the scaled impulse and the reciprocal of the scaled distance(Y=1)in this paper.Accordingly,N=2/3 proposed in this paper has a more theoretical base than those empirically adopted, as shown in previous works.
7.Conclusions
To address the lack of theoretical clarification and the controversial explanations for the available experimental results of ammunition explosion evaluation,the equivalent bare mass of the cased charge was theoretically analyzed.By establishing the energy conservation equation at the critical rupture moment of the casing,the evaluation correlations of the equivalent bare mass of the cased charge were obtained, and the relationship of the equivalent bare blast impulse of the cased charge was further theoretically deduced.The main conclusions are presented as follows:
1) The rationality of the proposed correlations in this paper is verified by comparison with the experimental results in the open literature.It is shown that the equivalent bare mass of the cased charge is related not only to the mass of the casing but also to the fracture strain of the casing and the type of charge.The fracture strain of the casing mainly affects the critical rupture radius of the casing, and the explosive type mainly affects the expansion process indicated by the polytropic expansion exponent.
2) The proposed correlations are constructed by theoretical deductions with key parameters validated by numerical simulations, in which all constants are determined with theoretical formulas rather than empirical constants adopted in existing correlations.Some controversial problems in the experimental results of the published literature are well explained by new correlations.
3) Based on the new correlations, the evaluation difference of equivalent bare charge mass for ideal explosive and nonideal explosive can be theoretically explained as the effects of energy difference, which is more consistent with available experimental results.
4) Based on the theoretical correlations proposed in this paper,the corresponding impulse ratio correlation is also theoretically derived with the power exponent as 2/3 rather than those empirically adopted,as shown in previous works.The validation results indicate better agreements with experiments than with existing correlations.
Although the results obtained in this paper are encouraging,some deviations also exist between the evaluation results and the experiments since some simplification assumptions are also integrated in the correlations.More experimental measurements are encouraged to provide more validations for new correlations, and further improvements are underway.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A
The derivations and subsitutions of Eqs.(22) and (23).
The kinetic energy (EG) of the casing, the kinetic energy (Eg) of the detonation product and the internal energy (Ee) of the detonation product in the critical rupture state of the casing are expressed as follows, respectively
Substituting Eqs.(A1)-(A3) into Eq.(7), we have
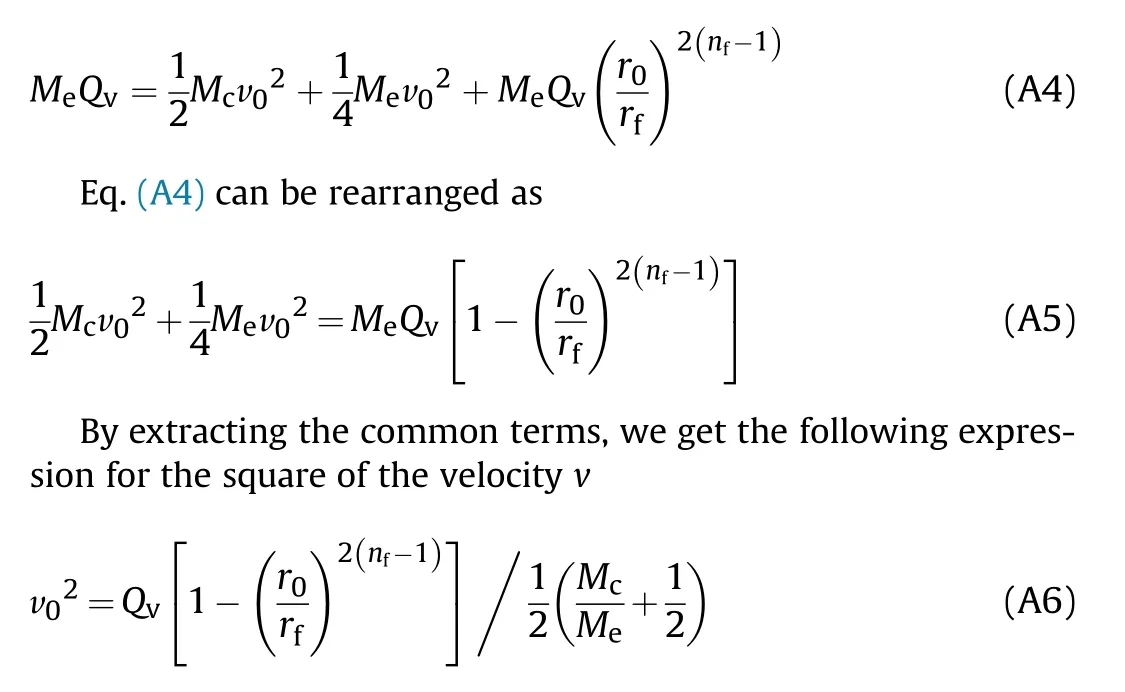
The total energy (Eg+Ee) of detonation products can be obtained by subtracting the kinetic energy(EG)of the casing from the total explosive energy MeQv
The ratio of the total energy of detonation products to the total explosive energy is equal to the ratio of the mass of the equivalent bare charge to the mass of the explosive[16].
The expression of Mb/Meobtained after combining Eqs.(A7)and(A8) is as follows:
Recalling that Eq.(A6)and substituting it into Eq.(A9),the final expression of Mb/Meis obtained as
Appendix B
The derivation of Eq.(26).
Simplification of Eqs.(24) and (25) leads to the following expressions, respectively
Combined with Eqs.(B1) and (B2), we have
Add r0to the left of Eq.(B3) and then subtract r0to change the Eq.(B3) to the following form
Recalling that Eq.(B2)and substituting it into Eq.(B4)we obtain

- Defence Technology的其它文章
- The dynamic response and damage models of rebar reinforced polymer slabs subjected to contact and near-field explosions
- Study of the axial density/impedance gradient composite long rod hypervelocity penetration into a four-layer Q345 target
- Active learning accelerated Monte-Carlo simulation based on the modified K-nearest neighbors algorithm and its application to reliability estimations
- Dynamic compressive response of porcine muscle measured using a split Hopkinson bar system with a pair of PVDF force transducers
- Damage of a large-scale reinforced concrete wall caused by an explosively formed projectile (EFP)
- Air target recognition method against ISRJ for radio frequency proximity sensors using chaotic stream encryption

