Air target recognition method against ISRJ for radio frequency proximity sensors using chaotic stream encryption
Jin-feng Li , Jin Di ,*, Xin-hong Ho ,b, Xio-peng Yn ,b, Xin-wei Wng
a Science and Technology on Electromechanical Dynamic Control Laboratory, School of Mechatronical Engineering, Beijing Institute of Technology, Beijing,100081, China
b BIT Tangshan Research Institute, Beijing,100081, China
Keywords:Interrupted-sampling repeater jamming(ISRJ)Radio frequency proximity sensors (RFPS)Chaotic stream encryption Air target recognition Identity (ID) decryption
ABSTRACT The interrupted-sampling repeater jamming (ISRJ) can cause false targets to the radio-frequency proximity sensors (RFPSs), resulting in a serious decline in the target detection capability of the RFPS.This article proposes a recognition method for RFPSs to identify the false targets caused by ISRJ.The proposed method is realized by assigning a unique identity (ID) to each RFPS, and each ID is a periodically and chaotically encrypted in every pulse period.The processing technique of the received signal is divided into ranging and ID decryption.In the ranging part, a high-resolution range profile (HRRP) can be obtained by performing pulse compression with the binary chaotic sequences.To suppress the noise, the singular value decomposition(SVD)is applied in the preprocessing.Regarding ID decryption,targets and ISRJ can be recognized through the encryption and decryption processes, which are controlled by random keys.An adaptability analysis conducted in terms of the peak-to-side lobe ratio (PSLR) and bit error rate (BER) indicates that the proposed method performs well within a 70-kHz Doppler shift.A simulation and experimental results show that the proposed method achieves extremely stable target and ISRJ recognition accuracies at different signal-to-noise ratios(SNRs)and jamming-to-signal ratios(JSRs).
1.Introduction
A radio-frequency proximity sensor (RFPS) works in an ultrashort range with low power.However,its air target detection ability is severely threatened by interrupted-sampling repeater jamming(ISRJ).Fig.1 shows an air target detection and jamming scenario of an RFPS.The function of the jamming pod is to jam and cause the false target to the RFPS before it can detect and track the target.Once the signal transmitted by the RFPS is perceived by the target,the jamming pod in the target can generate the jamming signal for protecting the target from being detected and attacked [1], and thus the jamming area is usually between the RFPS and the target area.
ISRJ is a kind of instantaneous deceptive jamming approach that is highly coherent with the target echo.The jamming pod samples a short piece of the signal produced by the RFPS and immediately transmits it back with frequency or delay modulation.The processing gain of the pulse compression system of an RFPS is not sufficient to eliminate ISRJ; thus, the range profile peak of ISRJ exceeds the target detection threshold and finally causes a false target [2-6].Due to its high coherence with real target echoes, a jamming pod can generate different kinds of false targets while using relatively little power.These characteristics of ISRJ pose great challenges for target detection with RFPSs.In addition, since ISRJ can jam an RFPS during the current pulse period through immediate retransmission, it is difficult to effectively suppress ISRJ with typical anti-jamming designs,such as frequency agility and binary phase-coded pulse compression [7-9].Therefore, an effective air target recognition method against ISRJ is urgently needed for RFPSs to identify real targets and false targets caused by ISRJ.

Fig.1.The air target detection and the jamming scene in the self-defense of the target.
Zhang et al.[10]proposed an ISRJ recognition method based on phase-coded signal processing, the simulation has verified its applicability for recognizing and suppressing direct forwarding ISRJ,but the selection of phase-encoded signals has a great impact on the recognition performance.Ref.[11]suppressed ISRJ using the singular spectrum entropy function, the results showed that the proposed method can increase the target detection probability,but the embedded matrix which is designed based on the simulation data may not work well in the real target detection scenario.The statistical features of the HRRP of radar were applied for jamming and target recognition [13], which improved the recognition accuracy.Ref.[14] extracted frequency entropies and peak-to-peak ratios for target recognition.Ref.[15] proposed an anti-jamming method for airborne radar based on moving target detection and feature extraction.Numerical results had been provided to verify the efficiency of the proposed algorithms.Ref.[16] presented an adaptive anti-jamming method based on a game model, the antijamming strategies are dynamically adopted according to their payoffs, but its anti-jamming performance against ISRJ is not discussed.Ref.[17] proposed a specific feature extraction method for characterizing radar systems, and it can be used for recognizing jamming signals and target echoes.Refs.[18,19]use empirical mode decomposition (EMD) and quadratic time-frequency analysis methods to extract fingerprint characteristics in waveforms, and the simulations verified its high efficiency.Wu et al.[20] used variance values to classify ISRJ signals and target echoes, and numerical experiments verified the promising performance of this approach.Wen et al.[21]utilized a time-space domain information fusion method for radar signal identification; this approach could deal with uncertain information when processing a radar signal.However,their recognition accuracy was sensitive to noise,limiting the applicability of their approach at low SNR.
In addition, convolutional neural networks [22,23] were increasingly applied to perform target and jamming signal recognition for radar sensors.The results yielded a high recognition accuracy for targets and jamming signals,but the computational complexity is still a major issue limiting their applications on RFPSs.Besides,some aperiodic waveforms had been designed against jamming.Refs.[24,25]proposed chaotic modulated waveforms to suppress the ISRJ effectively.A frequency-hopping waveform had been designed in Ref.[26] for target recognition, and the jamming could be identified through the frequency-hopping pattern presented in the article, but it only discussed its application on a multiple-input multiple-output radar system.Hanbal et al.[27] proposed a waveform agility method against the ISRJ with frequency shifting.Although the simulation has proved its effectiveness, the lack of experimental verification makes it difficult to verify the performance of the algorithm in real jamming scenarios.
Motivated by the gaps in the existing literature mentioned above,a new method using chaotic stream encryption is proposed in this article to improve the air target recognition performance against the ISRJ, especially when the JSRs and SNRs deteriorate.Innovation and contribution in this work can be summarized as follows:
1) We designed a unique ID for each RFPS based on the analysis of the influence of the ISRJ on the RFPS.The RFPS ID is encrypted intentionally in the transmitted signal with the binary chaotic sequence, which enables the RFPS to contain unique information in its transmitted signal.
2) The HRRPs of typical multi-scattering air targets are obtained,and the resolution of the designed waveform is analyzed and verified by pulse compression with the designed binary chaotic sequence.In addition,the SVD method is applied to suppress the noise of the HRRP,and it is also helpful for the following target recognition.
3) We proposed an air target recognition method using chaotic stream encryption.Once the target echo or jamming is received,the ID contained in the target echo can be decrypted by the reference decryption chaotic sequence, and thus the target can be identified.Although the ISRJ also contains repeated segments of the RFPS signal,the ID and encryption sequences are partially lost and messed up due to the retransmission mode of the ISRJ.Therefore, the target and false targets caused by ISRJ are recognized.The Monte Carlo simulations show that the target recognition accuracy of the proposed method maintains a high level greater than 90% at different SNRs and JSRs.
The rest of the paper is organized as follows.Section 2 introduces the transmitted signal design with chaotic encryption.In Section 3, the HRRP is introduced, and the air target recognition process using chaotic stream encryption is analyzed.The adaptability analysis is analyzed in Section 4.Experimental and Simulation results are illustrated in Section 5.The conclusions and extensions of future work are illustrated in Section 6.
2.Waveform design of a transmitted signal with chaotic encryption
The unique subtle features possessed by the transmitted signal of an emitter can be used to identify the echo and jamming signals.However, the subtle features of waveforms are unstable and difficult to extract, especially at low SNRs.Therefore, a unique ID that consists of 7-bit ASCII codes is designed for every RFPS, and there are 27kinds of RFPS IDs.
The RFPS ID is expressed as
where PτMrefers to a unit pulse,of which width is τMand yn∊{0,1}is the binary code of the given RFPS ID.Fig.2 shows the pulse code modulation (PCM) process of the RFPS ID.
To ensure the confidentiality of the ID,it should be encrypted in the waveform of the RFPS.The available encryption methods can be divided into block encryption and stream encryption [28,29].The confidentiality of block encryption is high, but its avalanche characteristics and high computational complexity limit its application in RFPSs.Stream encryption continuously encrypts the given data bit by bit and thus has the advantages of a simple structure and low computational complexity.High randomness and diversity are required for encryption sequences so that the cipher text can be effectively protected.Chaotic systems are widely used in encryption because of their good randomness and initial value sensitivity,which guarantee the feasibility of generating a large number of different chaotic sequences[30,31].The Henon map[32]is a typical chaotic map that can be expressed as
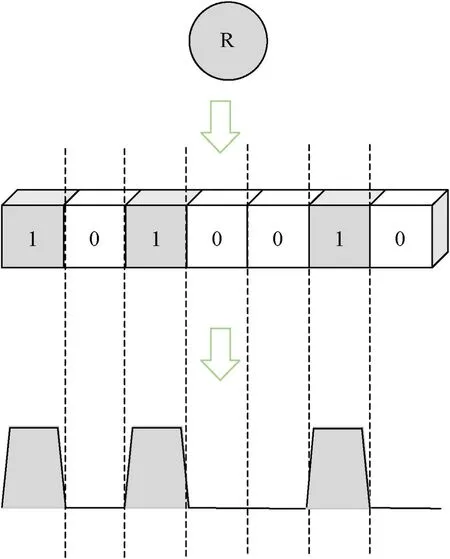
Fig.2.PCM process of the RFPS ID, e.g.ID = ”R”.
where a∊[0,1.4] and β∊[0.1,0.3] refer to the bifurcation parameters of the Henon map.Then, a binary chaotic sequence can be obtained through the conversion in Eq.(3).
where Zk(t)is the binary chaotic sequence,k is the random key that can control the generation of the binary chaotic sequence(which is determined by the values of a and β), N and τZare the length and width of Zk(t),respectively,and τZ=τM/N.zn(k)is the binary code of Zk(t),and zn(k)∊{0,1}.
Then, the RFPS ID will be encrypted with Zk(t), and the encrypted sequence can be expressed as
where Ekis the encryption algorithm with the key k, ⊕is the exclusive-OR operator, Ciis the encrypted ID and Ci∊{0,1}.
The final RFPS signal that has been chaotically encrypted is
where Utand Tmare the amplitude and pulse width of St(t),respectively,and Tm=7NτZ.ω0is the carrier frequency.The period of the RFPS ID is Tr, and K = 0,±1,±2,….
The encrypted chaotic sequences Zk(t) are aperiodic as the key changes in every ID period.The processes of modulation and encryption are shown in Fig.3.
3.Ranging and air target recognition against ISRJ with chaotic sequence and id decryption
The process of obtaining the received signal can be divided into two parts: ranging and ID decryption, as shown in Fig.4.In the ranging part, the HRRP is obtained through pulse compression.In the ID decryption part,the ID of the RFPS is obtained via the chaotic decryption process.
3.1.High-resolution ranging by pulse compression with the encrypted binary chaotic sequence
An ambiguity function is an effective tool for measuring the detection performance of a signal.The complex envelope of a transmitted signal St(t) is
The single-period ambiguity function of the waveform based on chaotic stream encryption can be deduced as

Fig.3.Modulation and encryption processes of the encrypted RFPS signal.
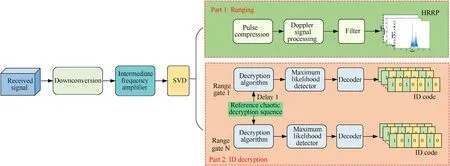
Fig.4.Block diagram of the ranging and ID decryption processes for the RFPS.
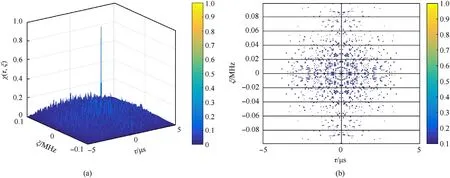
Fig.5.The 3D map and contour of the ambiguity function for the proposed signal: (a) 3D map of the ambiguity function; (b) The contour of the ambiguity function.
where τ and ξ refer to the time delay and frequency offset,respectively.Fig.5 shows the 3D map and contour of the ambiguity function for the proposed signal, and the thumbtack ambiguity map shows the high resolution of the waveform encrypted with the chaotic sequence.
To verify the ranging performance of the proposed sequence,the multi-scattering target echoes are collected.The demodulated signal from a multi-scattering target consisting of Kr scatters is expressed as
where τxand Uxare the delay and amplitude of the echo of the xth scatter, respectively.ωdand φrrepresent the Doppler angular frequency and the initial phase of Srm(t).
The range profiles can be obtained by pulse compression with the encrypted binary chaotic sequence, as shown in Eq.(9).
where Amis the amplitude of the reference signal,τpis the preset delay time for the local reference signal,p =1,2,…,P,and P is the number of range gates.
To test the ranging performance of the designed signal, the multi-scattering models of two typical air targets are built using the physical optics (PO) method.Fig.6(a) and 6(c) are the scattering models of different targets,and Fig.6(b)and 6(d)are the HRRPs of targets obtained by conducting pulse compression on the proposed signal.The results show that the proposed signal can achieve highrange resolution for typical air targets through pulse compression with the chaotic sequence.
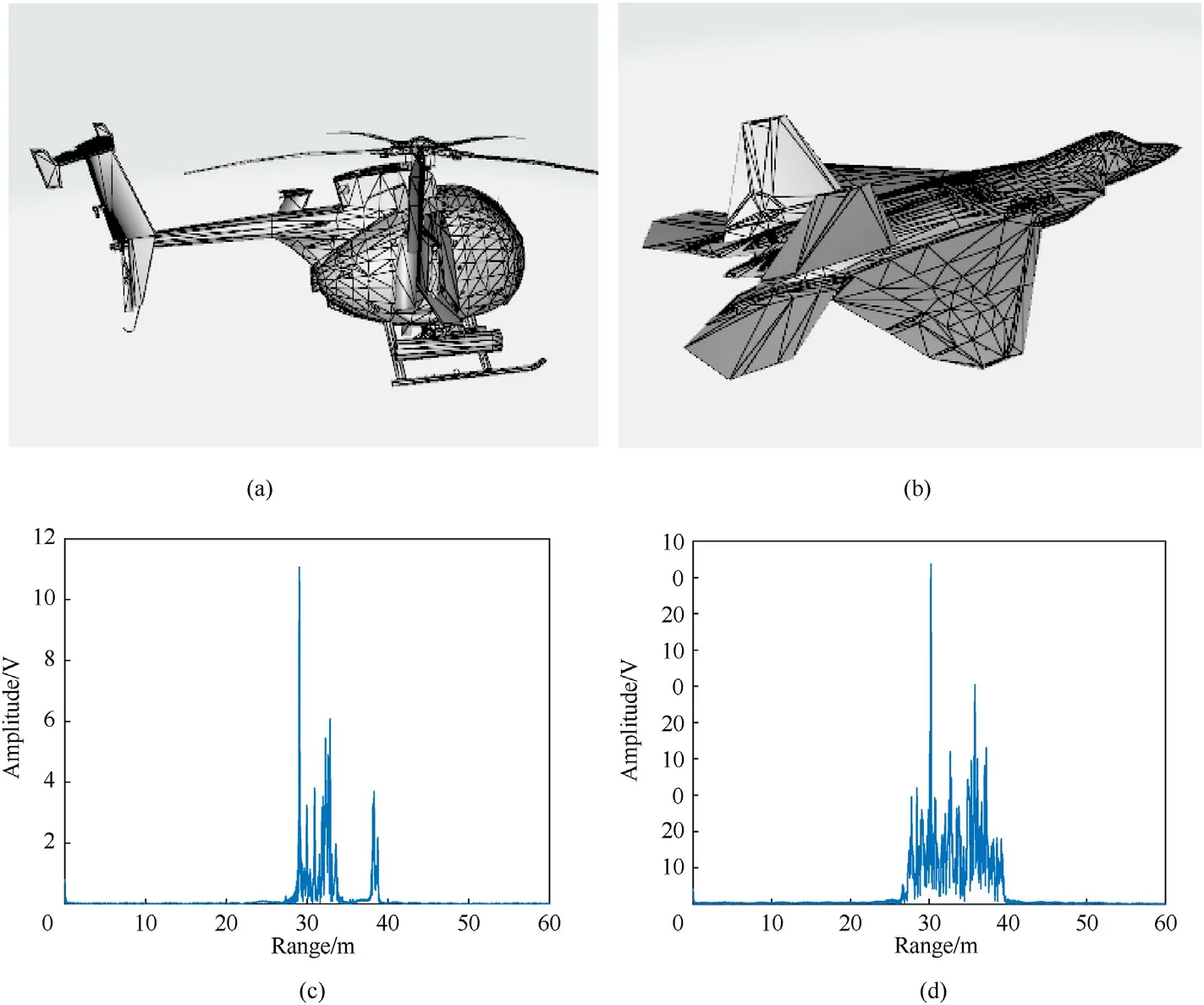
Fig.6.The HRRPs of two targets obtained by pulse compression with the encrypted binary chaotic sequence:(a)The multi-scattering model of a helicopter;(b)The multi-scattering model of a fighter; (c) The HRRP of the helicopter target; (d) The HRRP of the fighter target.
3.2.Preprocessing using SVD
The clutter and noise are harmful to target detection, and it is necessary to suppress the clutter and noise for target detection.SVD is an important matrix factorization in linear algebra,and has been applied in denoising.The SVD method decomposes signals according to the value of the signal components.The clutter and noise will be significantly suppressed by setting the small and useless signal components to 0.The primary step of SVD is to construct the Hankel matrix A,α is the discrete signal sequences.

The singular value of matrix A is the arithmetic square root of q non-negative eigenvalues of AAHor AHA, as shown in Eq.(13).
The value of σiis related to the energy of the signal component it represents.Generally, the target signal has a big singular value while the clutter and noise have a small singular value, thus they can be suppressed by setting small singular values to 0.Assume that A(k)=UΣkVH≈A , Σk=Σki=1σicontains k largest singular values, and others are set to 0.The value of k can be obtained through the following steps:

Step 3.break and return the value of k,where T is a threshold which is close to 1.In Fig.7(b)-(d), we reserve different biggest singular values of the Hankel matrix(k=7,5,and 3).As shown in Fig.7,the smaller the value of k is,the better the noise suppression performance,but the target profile will also be affected.Therefore,the value of k needs to be determined according to specific requirements.
3.3.Air target recognition through chaotic RFPS ID decryption
Generally,there are three typical kinds of retransmission modes for ISRJ signals, including the repeated retransmission mode, the direct retransmission mode,and the periodic retransmission mode,as shown in Fig.8.
In the repeated retransmission mode,the jamming pod samples a piece of the signal of the RFPS and repeats it until reaching the next sample.In the direct retransmission mode, the jamming pod retransmits the last samples of the signal directly without repetition.In the periodic retransmission mode, all previous samples of the signal are retransmitted during each sampling interval.The jamming signal pieces provided by the three retransmission modes are repeated and arranged in different patterns,forming a different false target distribution in the range profiles through pulse compression, as shown in Fig.9.
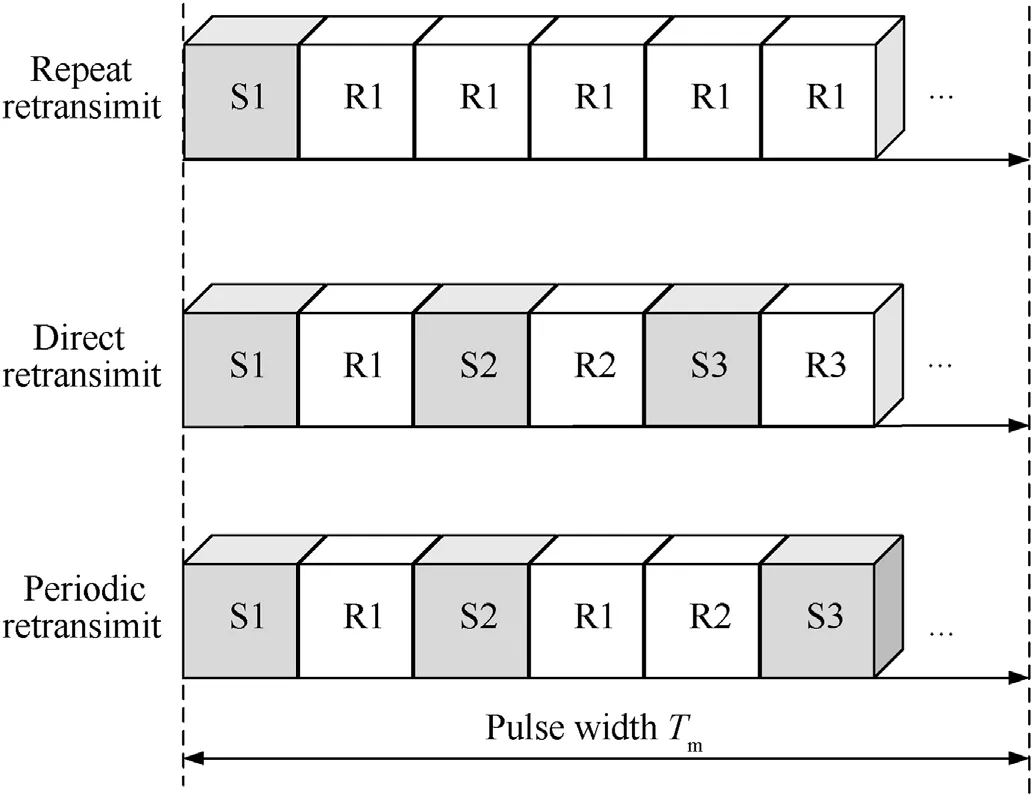
Fig.8.The three typical retransmission modes for ISRJ signals.
Fig.9 shows that the ISRJ signals can generate densities and variable false targets through different retransmission modes with frequency and delay modulation.In addition, the amplitude of a false target may exceed that of the real target while the ISRJ signals are transmitted with high power.Therefore, the RFPS is unable to recognize the target and ISRJ through the amplitude of the range profile alone.
To distinguish the real target from the false target caused by ISRJ,this article designed a method using chaotic stream encryption and decryption.The complete recognition flow is shown in Fig.10,Once the target echo or ISRJ is received by the RFPS,the target echo or jamming signal will be decrypted by the reference chaotic decryption sequence in the binary maximum likelihood detector.Next, the decoder will transfer the binary code to the ASCII code(which is the decrypted ID).Finally, the decrypted ID is compared with the ID of the RFPS.The target echo is recognized only if the decrypted ID is equal to the ID of the RFPS, otherwise will be recognized as jamming.Herein, the ID of the RFPS is set as “R” for example.
To obtain the RFPS ID from the target echo, the demodulated signal Srm(t) need to be decrypted by the reference chaotic decryption sequence Zk
(t-τp
).The decrypted ID sequence through the binary maximum likelihood detection is


where Ajand ωjrefer to the amplitude and carrier wave frequency of ISRJ,Δτjis the modulated delay of the ISRJ,Tjrepresents the ISRJ retransmit period.Once the RFPS receives an ISRJ signal, the downconversion output in a single retransmission period can be expressed as
where Ajmandωjmare the amplitude and carrier frequency of the ISRJ signal generated by the jamming pod,respectively.Δτjmrefers to the transmission delay, CJ(t-Δτjm) denotes the encrypted sequences intercepted and repeated by the jamming pom, the original phase of the jamming signal is φjm,and φjmcan be set to 0 for the convenience of analysis.Next, Sjm(t) is decrypted by the local binary chaotic decryption sequences,and the decrypted sequences are

The decryption result is shown in Fig.11 for the verification of the decryption process.The ASCII code“R”is assigned to the RFPS,and the transmitted ID is shown in Fig.11(a).Once the echoes of air targets are received by the RFPS, they are decrypted with the reference chaotic decryption sequence Zk
(t-τp
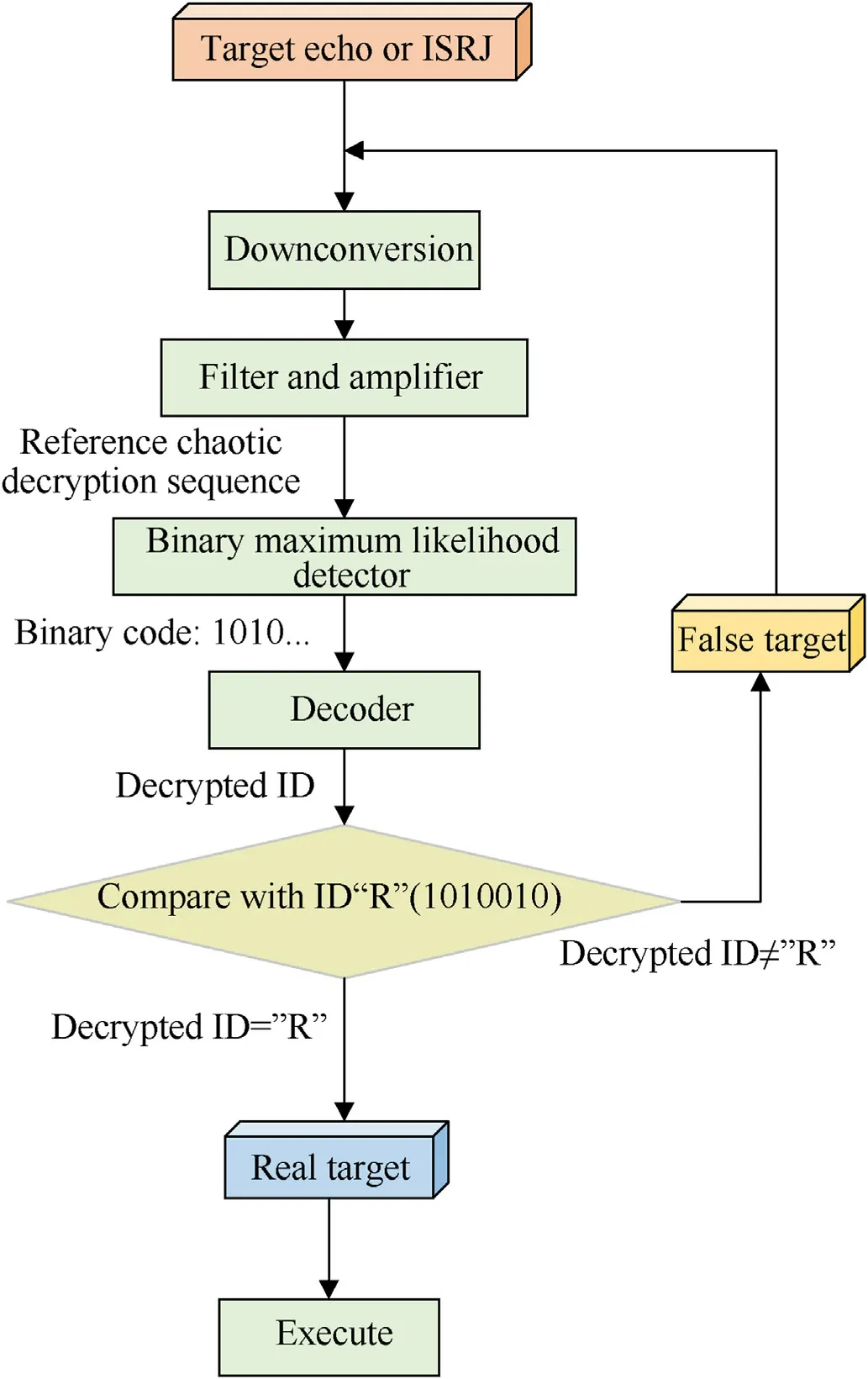
Fig.10.The identification flow of target and ISRJ based on ID decryption and recognition.
).The decrypted IDs obtained from the echoes of the two targets shown in Fig.11(b)and 11(c) are the same as the transmitted ID of the RFPS, which means that the received signal is derived from the target,and thus the target echoes are recognized.Fig.11(d)is the decrypted ID from the ISRJ,which shows that the decrypted ID is not“R”.The reason is that even if the ISRJ contains repeated segments of the RFPS signal,the ID and encryption sequences are partially lost and messed up because of the retransmission mode of the ISRJ.Therefore, the target and false targets caused by ISRJ can be recognized through the decrypted ID.
4.Adaptability analysis
4.1.BER analysis
The recognition accuracy is mainly affected by the bit error rate(BER) that can be obtained by the complementary error function[33].Fig.12 shows the BERs yielded at different processing gains(G)and SNRs,and G =This shows that the BER is relatively low and that the proposed method can achieve high ID recognition accuracy when G ≥10 and SNR ≥- 10 dB.
According to Eqs.(9) and (13), the pulse compression and ID decryption processes are affected by the Doppler frequency.For the pulse compression process, the processing gain and the PSLR deteriorate if the Doppler shift is relatively high.For the ID decryption process,a high Doppler shift leads to a false result being produced by the correlation detector, and thus, the BER also rises.Therefore,it is necessary to study the influence of the Doppler shift on pulse compression and the ID decryption process.Herein, we adopt the PSLR and BER to measure the performance of pulse compression and ID decryption.
4.2.Doppler tolerance analysis
The PSLR is typically used to measure the quality of pulse compression properties, and the PLSR of the binary chaotic sequence C(t) is expressed as Eq.(20).Large PSLR values indicate better pulse compression properties.
where σ and u refer to the standard deviation and mean of the correlation-side lobe region of C(t), respectively.In the pulse compression process, the PSLRs of C(t) at different Doppler frequencies and sequence lengths N are shown in Figs.13 and 14.
As shown in Fig.14, the Doppler tolerance decreases as the sequence length increases.When N = 100, the PSLR rapidly decreases when the Doppler shift is higher than 70 kHz,and the HRRP obtained through pulse compression is severely affected.
Moreover, the BERs of the ID decryption process at different Doppler shifts and sequence lengths are shown in Fig.15.The BER increases rapidly when the Doppler shift exceeds 70 kHz,which is consistent with the PSLR in Fig.14.Therefore,the proposed method can perform well within a 70-kHz Doppler shift.
4.3.Complexity analysis
The bit-wise-exclusive-OR in the encryption and decryption process can be regarded as an addition modulo 2 operation, the N chips modulo 2 operations include N times addition operations.If the complexity of an addition operation is defined as,and then the algorithm complexity of the N chips modulo 2 operations can be defined as Therefore,the complexity of an encryption or decryption process is.The durationof thetarget signal iscorrelated withthe chip widthτZ, thatisDur=, herein,τZis setto 20 ns,v =1000 m/s,and thus the Duris 6 ms.Then,the Tris set to 10 μs,thus the number of periods within the duration of the target signal is 100.Therefore, the time complexity within the duration of the target signal can be expressed as

Fig.13.The PSLRs of the binary chaotic sequence C(t):(a)N=50,Doppler shift=50,60,70,80 kHz;(b)N=75,Doppler shift=50,60,70,80 kHz;(c)N=100,Doppler shift=50,60, 70, 80 kHz.

Fig.14.The PSLRs of ur(t).
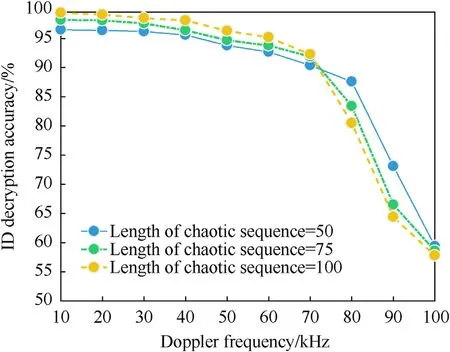
Fig.15.The BERs of the ID decryption process with Doppler frequencies ranging from 10 to 100 kHz and N = 50, 75,100.
The space complexity mainly depends on the number of chaotic sequences and sample rate fswithin the Dur, and the space complexity can be expressed as
If the signal processing chip system clock is 100 MHz, fs= 109Hz and N = 20, it will only take about 0.14 ms and 280 K bits of storage space to complete the encryption and decryption operation within the Dur,and it can fully meet the real-time and storage space requirements of the RFPS.
5.Experiment and simulation results
In the simulation,200 sets of ISRJ samples and 200 sets of target scattering samples are generated by a jamming pod and a target scattering model,respectively.Considering a practical scenario,the velocity v of the RFPS is set from 150 to 1200 m/s;thus,the Doppler frequency range from 10 to 80 kHz.The SNR is usually not too low because the RFPS works in a relatively short range.Herein, we set the SNR from-10 to 0 dB.The simulation parameters are shown in Table 1.

Table 1Simulation parameters.
To test the stability of ranging with the proposed method, the simulation obtains the HRRPs of the two targets at different SNRs.According to the practical situation,the SNR is set from-10 to 0 dB,and the HRRPs are obtained by pulse compression with chaotic sequences.As shown in Fig.16, the proposed method obtains the HRRPs of the target at different SNRs.
For the verification of the target and ISRJ recognition performance of the proposed method, a countermeasure experiment is carried out in an anechoic chamber.In this anechoic chamber, the prototype of the proposed RFPS is placed opposite the jammer, as shown in Fig.17(b) and 17(c).80 sets of immediate data obtained under the action of ISRJ and targets are collected for the subsequent analysis.
The results of the countermeasure experiment are shown in Table 2.The recognition accuracy is defined as
where NTPmeans the number of target samples classified as target,NTNmeans the number of jamming samples classified as jamming,Nsis the number of the test samples.The results show that the target and ISRJ can be identified via ID recognition, and thus, the feasibility of the proposed air target recognition method is verified.
To further evaluate the recognition performance of the proposed method at different SNRs, several typical anti-jamming methods and new anti-jamming methods are compared through 500 times Monte Carlo simulations; these approaches include pulse compression methods that utilize Barker codes and m sequences(Barker-based and m sequence-based, respectively), the ISRJ recognition method based on phase-coded signal processing (PCbased) in Ref.[10], the singular spectrum entropy method (SPEbased) in Ref.[11], the waveform agility method against ISRJ in Ref.[12], and the ISRJ recognition method based on integration decomposition(FTRID-based)in Ref.[26].The results are shown in Fig.18.
As shown in Fig.18, the air target recognition accuracy of the proposed method remains stable,while those of the other methods decrease rapidly as the SNR deteriorates, which means that the proposed method can adapt to low-SNR scenarios.

Fig.16.The HRRPs of the two targets at different SNRs obtained by using the proposed method: (a) The HRRPs of the helicopter at different SNRs; (b) The HRRPs of the fighter at different SNRs.

Fig.17.The scene of the countermeasure experiment: (a) The prototype of the RFPS and its signal processing module; (b) The target simulator; (c) Experiment in the anechoic chamber; (d) The jammer and its antenna.
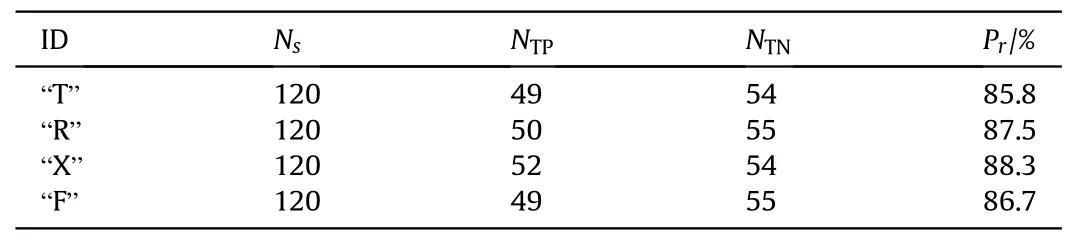
Table 2The target and ISRJ recognition results of the countermeasure experiment.

Fig.18.The air target recognition accuracy comparison at different SNRs.

Fig.19.The air target recognition accuracy comparison at different JSRs.
In addition,JSR represents the instantaneous power of jamming with respect to the target echo.It is flexibly controlled by the jamming pod via a power amplifier.Generally, the jamming pod amplifies the power of the retransmission signal to achieve better jamming performance.The false target peak caused by ISRJ can be higher than the target echo peak.Therefore, the recognition accuracies of these methods at different JSRs are compared,as shown in Fig.19.Considering the practical scenario, the JSR is set from 0 to 40 dB.
In Fig.19,as the JSR increases from 0 dB to 40 dB,the recognition accuracy of the proposed method remains at a high level, while those of other methods decrease rapidly.The reason for this is that the amplitude of jamming does not influence the polarity of the decrypted ID sequence Mjm(t) shown in Eq.(18), and thus, the decryption result of the proposed method is independent of the signal or jamming power.Therefore, the decrypted ID remains stable so that the RFPS can identify air target echoes and ISRJ.
6.Conclusions
In this article, an air target recognition method against ISRJ is proposed.Each RFPS is assigned a unique ID that is chaotically encrypted in every transmission period.To verify the ranging performance,multi-scattering model are established using PO method,and a pulse compression process that uses encrypted binary chaotic sequences to obtain the HRRPs of targets is introduced.To suppress the clutter and noise, the SVD method is applied in the preprocessing.The ID recognition process of air target recognition is analyzed.The encryption and decryption chaotic sequences in every ID period,which are controlled by the random key,guarantee the recognition of the air target and ISRJ in a highly efficient manner.The Doppler tolerance of the proposed method is also analyzed by using the PSLRs and BERs obtained at different Doppler frequencies and sequence lengths.A simulation and an experiment involving a jamming pod and a prototype RFPS are carried out,and the air target recognition accuracies of different methods are compared.The experimental results verify the high-range resolution and strong stability of the proposed method at different SNRs and JSRs.
It should be noted that the proposed ID decryption and target recognition method is only applicable to phase-coded wave, other waveforms and modulation types, such as frequency-modulated continuous wave and pulse Doppler RFPS, are not applicable.Furthermore,the correlation side lobes are related to the selection of the chaotic sequences.To select the optimal chaotic sequences with the smallest correlation side lobes, future work will focus on the optimization of chaotic sequences.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No.61973037) and (Grant No.61871414) and Postdoctoral Fundation of China (Grant No.2022M720419).
- Defence Technology的其它文章
- The dynamic response and damage models of rebar reinforced polymer slabs subjected to contact and near-field explosions
- Study of the axial density/impedance gradient composite long rod hypervelocity penetration into a four-layer Q345 target
- Active learning accelerated Monte-Carlo simulation based on the modified K-nearest neighbors algorithm and its application to reliability estimations
- Dynamic compressive response of porcine muscle measured using a split Hopkinson bar system with a pair of PVDF force transducers
- Damage of a large-scale reinforced concrete wall caused by an explosively formed projectile (EFP)
- New correlations for evaluating the equivalent bare charge mass for a cased charge

