Dynamic compressive response of porcine muscle measured using a split Hopkinson bar system with a pair of PVDF force transducers
Yo-ke Wen , Ling Xu , Ai-jun Chen , Fng-dong Dong , Bin Qin
a School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China
b School of Science, Nanjing University of Science and Technology, Nanjing, 210094, China
c Science and Technology on Transient Impact Laboratory, Beijing,102202, China
Keywords:PVDF Hopkinson bar Porcine muscle Dynamic mechanical properties Constitutive model
ABSTRACT The classic metallic Split Hopkinson Pressure Bar(SHPB)cannot capture the transmitted signal accurately when measuring soft biological tissue, because of the very low wave impedance and strength of this material.So the dynamic compressive response of porcine muscle has been investigated by using a modified SHPB.The forces on both ends of the sample measured using Polyvinylidene fluor (PVDF)transducers were applied to calculate the stress in the specimen instead of the strain gauge signal on the transmitted bar.Moreover, a circular cardboard disk pulse shaper was applied for generating a suitable incident pulse to achieve stress equilibrium and constant strain rates in the specimens.Then, the dynamic mechanical properties of porcine muscle parallel and perpendicular to the fiber directions were measured,and the stress equilibrium process during loading was analyzed,as well as the inertia-induced extra stress being corrected.Furthermore, quasi-static tests were conducted at two different strain rates to investigate the strain rate dependence using a universal material testing machine.The results show that the stress-strain curves are sensitive to strain rate in the two different loading directions.The compressive stress perpendicular to the fiber direction is stiffer than that parallel to the fiber direction.In addition,a strain rate-dependent constitutive model was developed based on the mechanical response of the muscle at different strain rates and fitted to the experimental data.The results show that the overall fit is good, and the constitutive model could describe the muscle's dynamic mechanical properties.
1.Introduction
Behind armor blunt trauma (BABT) is increasing rapidly on the modern battlefield.To understand the injury mechanisms and to design advanced armor, it is necessary to investigate the dynamic response of biological tissues quantitatively.The SHPB system is the most popular apparatus for determining the mechanical properties of materials under high-rate loading [1].However, several problems arise when conducting soft materials testing, such as biological tissues, rubbers, and foams using SPHBs [2,3].
The first is the impedance mismatch effect of soft materials and SHPB bars[2,4].Being only a tenth of that of metal materials as the wave impedance of biological tissue is,most of the impact pulse is reflected back into the incident bar, with only a tiny portion being transmitted into the transmission bar.As a result, regular resistor strain gauges cannot accurately capture the weak transmitted signal in the metallic transmission bar.The actual transmitted signal will be of similar magnitude to the noise[2,5,6].Secondly,it is difficult for a soft material specimen to achieve stress equilibrium during the loading process of the SHPB system[7-9].It needs thin specimens and additional measures to achieve equilibrium because of low elastic sound velocity in soft materials [10,11].Therefore, a modified SHPB system for dynamic mechanical testing of soft materials is needed.In previous studies, varieties modified SHPB methods have been proposed to overcome the obstacles mentioned above [1,12,13].Enhancing the transmitted strain signal amplitude and directly measuring the force on the ends of the specimen are the main technological approaches [1].
An alternative approach for calculating the stress in the specimens is to use the average value of contact force on both the specimen-bar interfaces instead of the weak transmitted strain signal.Quartz crystal disks and PVDF piezoelectric thin films are the most popular transducers to measure the contact force [14].PVDF transducer is more frequency-responsive and thinner than the quartz sensor.Furthermore, PVDF transducers can be placed between the specimen-bar interfaces, but an additional aluminum disc must be used when detecting the force with crystal gauges[7,14,15].To minimize the inertia induced stress in the soft specimens during the SHPB experiments,the thin annular specimen and the circular cardboard pulse shaper were adopted.In addition,the experimental data were corrected with a theoretical formula to obtain high-fidelity results [1,7,12].
In this article, the dynamic compressive response of porcine muscle was determined by using PVDF force transducers in our aluminum alloy bar SHPB system.For both parallel and perpendicular to fiber directions, the stress-strain curves of porcine muscle at high strain rates were investigated.The stress equilibrium process during loading was analyzed, and the inertia effect was corrected with the experimental results being discussed as well.
2.Experimental method
The experimental setup of the modified SHPB system is shown in Fig.1 [14].The system consists of an aluminum striker, incident and transmission bars.Semiconductor strain gauges (Model SYP-120, CDLM instrument Co., Ltd.) glued onto the incident bar were used to record the incident and reflected strain signals.The classical SHPB setup was complemented by two PVDF force transducers(Jinzhoukexin Inc.) on both specimen-bar interfaces.The PVDF is too thin (only 0.2 mm) to affect the elastic stress wave during loading.A high-speed data acquisition system (Model LK2400,LKCK Co., Ltd.) with sample rate 5 MHz was used to record the output voltages from the strain gauges and both PVDF transducers.
Different from the classical method,the proposed method uses a single strain signal and two contact force signals to determine the stress, strain and strain rate during loading.The derivation of this new method is shown below [14].
The stress(σ)in the specimen could be calculated based on the contact forces F1and F2on both the specimen-bar interfaces,which can be directly measured by the PVDF force transducers
where A0is the initial cross-sectional area of the specimen.
The relationship between the two contact forces and incident strain εI, reflected strain εRand transmitted strains εTare as follows:
where Ebis the Young's modulus of the Hopkinson bar,and Abis the cross-section area of the Hopkinson bar.
The dynamic equilibrium requirement is expressed as
which indicates that the use of the reflected signal εRand the two force transducers signals are sufficient to determine the dynamic properties of a soft material (without the transmitted signal).
3.The experimental process
In the experimental setup used in this study, all the bars are made of aluminum alloy(7A04-T6)with diameters of 14.5 mm.The lengths of striker, incident and transmission bars are 400 mm,1500 mm,1500 mm, respectively.The semiconductor strain gage glued at the middle of the incident bar was used to record the reflected strain signal.Lubricating oil was smeared on both sides of the PVDF force transducers to reduce friction.Then the PVDF force transducers were put on the front and back specimen-bar interfaces to record the contact force during loading.The sampling frequency of the digital recording system is 5 MHz.

Fig.1.Schematic of the SHPB system.
Fresh porcine thoracic muscle was purchased from a local butcher shop.Thin-disc specimens were used to speed up the dynamic stress equilibrium process.The muscle was sliced into 2.5 mm thick flat sheets parallel and perpendicular to the muscle fiber directions by using an electric food slicer.Then muscle sheets were cut into 8 mm diameter thin-disc specimens using trephine blades with very sharp edges[7].The porcine muscle specimens are shown in Fig.2.During the loading process, when the diameter of the specimen reaches 14.5 mm, the thickness of the specimen is 0.69 mm at this time, and the engineering strain is 0.7.In order to achieve early dynamic stress equilibrium state and nearly constant strain rate,a circular piece of cardboard was used as a pulse shaper to generate an initially slow loading profile in the incident pulse[4,16].Each strain rate curve is achieved by averaging at least three sets of valid data.
4.The experimental results validation
4.1.Equilibrium state in the specimen
A series of experiments on the muscles from the porcine thoracic region were conducted with the improved SHPB device.It is necessary to make sure that the specimen has reached dynamic stress equilibrium by comparing the two PVDF transducers signals at both the specimen-bar interfaces during an experiment to ensure the accuracy of results.Fig.3 shows the original waveforms recorded using the PVDF transducers placed on both specimen-bar interfaces.The front end force F1is significantly higher than the back end force F2during the time from 0.17 ms to 0.25 ms, indicating that dynamic equilibrium was not reached at both ends of the sample in this time interval.The bulge at this stage is caused by the inertia effect of the specimen, which will be discussed in the next section.After 0.25 ms, the two force curves at the front and back end faces of the specimen overlap each other, indicating that the dynamic equilibrium state in the specimen may have been achieved during the impact loading.

Fig.2.Photograph of thin-disc porcine muscle specimens.
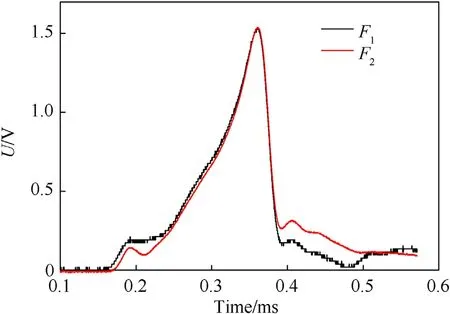
Fig.3.A typical set of original experimental waveforms obtained from the PVDF transducers.
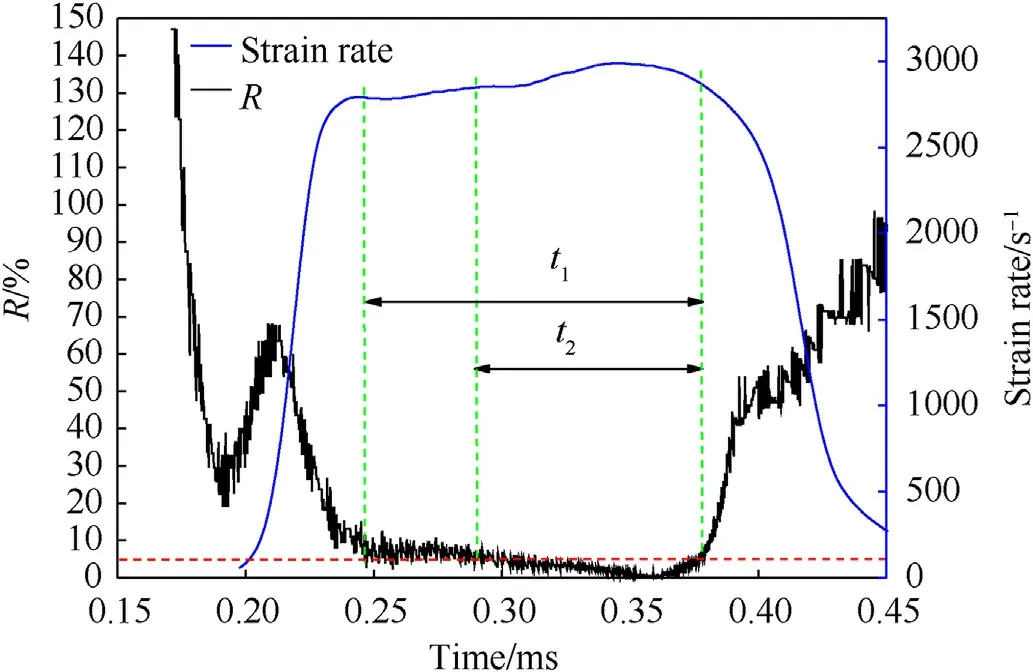
Fig.4.The time histories of strain rate and R in the porcine muscle specimen.
The stress equilibrium index R is defined in Eq.(8).It is generally believed that the dynamic equilibrium of the specimen would be reached when the R is less than 5%[17].In Fig.4,t1is the duration of constant strain rate, and t2is the duration from the beginning of stress equilibrium to the end of the constant strain rate.Here, the equilibrium state coefficient(λ=0.69)is defined as the ratio of t2=0.09 ms and t1= 0.13 ms.The closer that λ is to 1, the better the equilibrium state in the specimen will be.
4.2.Inertia correction
During dynamic axial compression, an extra-axial stress component is produced by the expansion of the specimen in the radial directions.This extra stress can mask the intrinsic mechanical response when the specimen material is very soft [18].In this paper, we adopt a stress-based approach to calculating the inertia effect proposed by Warren and Forrestal [19].Gorham et al.proposed an excellent energy-based approach to calculating the inertia effect in SHPB testing, which took the motion of both ends of the specimen into account[20,21].It has been shown that the energybased yield equivalent results with stress-based approaches [22].They differ in that the former uses engineering strain, while the latter uses the true strain.This inertia-induced extra stress σccan be corrected using Eq.(9)[19].In Eq.(9),the inertia-induced extra stress has two contributing factors: inertia due to the initial acceleration in specimen deformation and the high-rate deformation at large strains [23].
where ρ is the specimen density,r0is the initial specimen radius,¨ε is the strain acceleration in the specimen.
An abnormal bulge can be found at the early stage of the original stress curve in Fig.5.This indicates that the stress generated by initial acceleration may result in invalidation of the stress-strain curve of porcine muscle during the initial stages of loading.After an initial acceleration, the stress increases almost exponentially with the increase of strain, and the strain-rate inertia term is only accounting for a tiny portion.Therefore, the inertia correction should be taken into account in the dynamic mechanical testing of soft materials.

Fig.5.Comparison of raw result and corrected result at strain rate 4000/s perpendicular to the fiber direction.
5.Results and discussion
Through the above experimental methods, the engineering stress-strain curves of porcine muscle tissues have been determined at three high-rates.The quasi-static tests at strain rates of 0.01/s and 0.1/s were also conducted using a universal material testing machine(Model CMT6503,SANS Co.,Ltd.)to investigate the strain rate dependence.Fig.6 and Fig.7 exhibit the resultant compressive stress-strain curves of the porcine muscle tissue both parallel and perpendicular to the fiber directions.Furthermore,the stress-strain curves for porcine muscle at strain rates of 1900/s and 3700/s[7]are also included in the figures for comparison purposes.
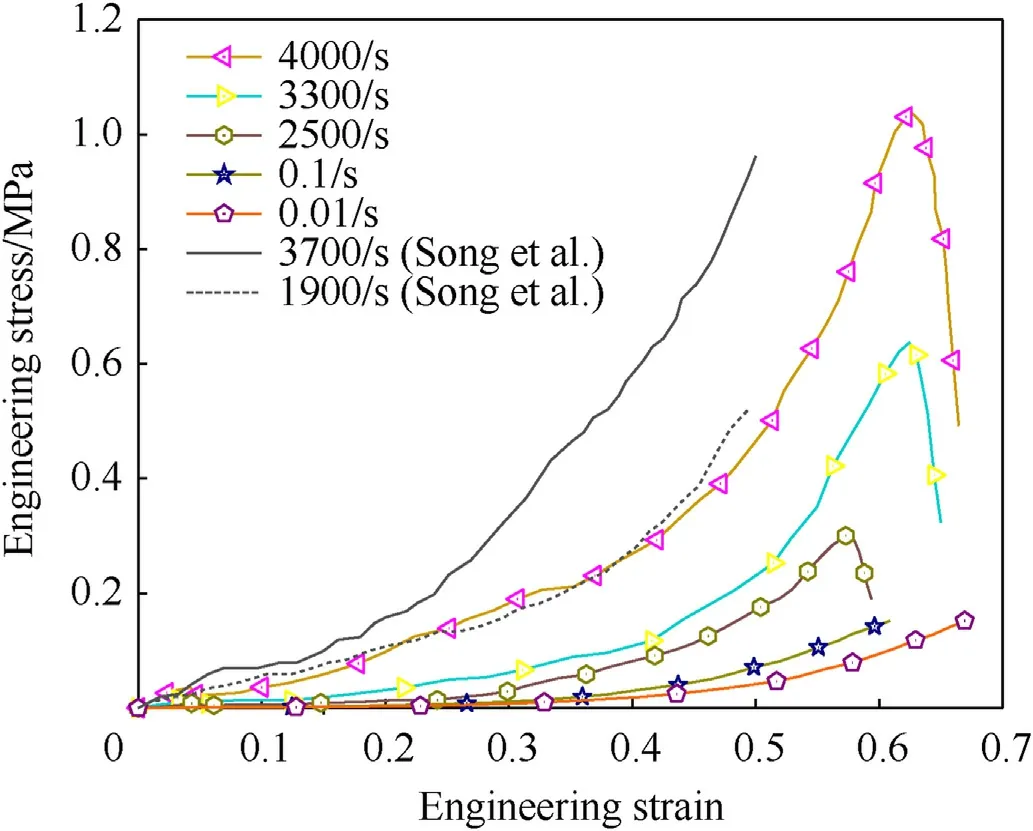
Fig.6.The resultant compressive stress-strain curves of the porcine muscle parallel to the fiber direction.
It is interesting to note that the porcine muscle is strain rate sensitive in both directions from quasi-static to high strain rate.All curves exhibit a toe region at the beginning, followed by a nonlinear response and then a strain hardening behavior [7].After the loading stage,the stress declines rapidly as the strain increases,which is due to the end of the pulse period but not the decay in the mechanical property of the specimen.It can be found in a given pulse length(striker length),the higher the strain rate is,the higher the maximum strain can be obtained in a given SHPB test.The decline cannot be observed in the quasi-static experiments as the load can continue to be applied indefinitely.The maximum specimen strain (εmax) in the SHPB test is equal to the multiple of the average strain rate value (˙ε) and the pulse duration time (tp=2L0/Cb) [24].L0is the length of the striker, Cbis the bar wave velocity.The consistency of the calculated value and the strain at the peak stress in Fig.6 and Fig.7 can prove the reliability of our experiment.When the strain rates were 2500/s,3300/s and 4000/s,the predicted maximum strains were 0.4, 0.53 and 0.64, respectively.Considering that the dispersion of results in soft tissue specimens is much greater than that in metal specimens, these values are reasonably consistent with the experimental results in Fig.6 and Fig.7.
The stress of porcine muscle at an engineering strain of 40%versus strain rate are plotted in Fig.8.By comparing with Song’s results in both directions, the quasi-static stress values are very close to each other,while our dynamic data are softer.Considering the differences in the samples and testing methods, it still makes sense.The shape of specimens we used in the dynamic experiments is a thin-disc of porcine thoracic muscle,while Song’s were circular taken from porcine ham.Furthermore,the stress calculated in this paper was based on the data from PVDF gauges, while Song used the transmitted strain to calculate stress.When compressed along the fiber direction, the fiber tends to buckling instability and unbearable.The compressive strength of muscle along with fiber direction is determined by the properties of connective tissue.When compressed in perpendicular to the fiber direction, the muscle fibers that are arranged in parallel and compacted will bear the pressure together with the connective tissue.Therefore, the strength of porcine muscle perpendicular to the fiber direction is stronger than that in the parallel fiber direction.As the strain rate increases, the stiffness of the muscle increases significantly.
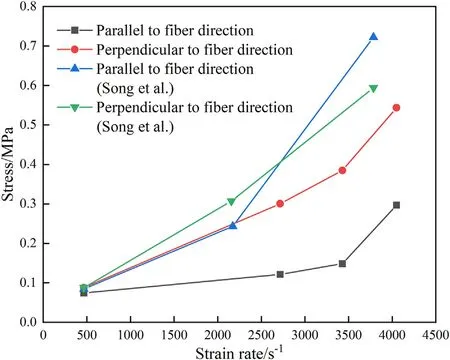
Fig.8.The stress data of porcine muscle at an engineering strain of 40% versus strain rate.
6.Constitutive model
6.1.Hyperelastic constitutive model
Muscles exhibit significant hyperelasticity under quasi-static conditions, and the constitutive relation of a hyperelastic material can be entirely given by its strain energy function W.The strain energy function can be decomposed into the following two components for isotropic materials, which are the strain bias energy and the volume strain energy, respectively.
where Ci0is the material parameter,N is the polynomial order,Diis the volume parameter.Rivilin generalizes the above equation using a polynomial approach to a more general form.
where Cijis the Taylor expansion coefficient.The volume strain can be zero for incompressible materials when J = 1.In this paper,muscle tissue is considered an incompressible material.Guetta and Rittel [25] considered the plastic deformation with strain hardening of the uniaxial tensile text, and proposed five improved constitutive models to describe the quasi-static mechanical properties of hydrogels according to Eq.(11).In this paper, the Yeoh hyperelastic constitutive model was used to describe the quasistatic mechanical properties of porcine muscle.
Yeoh assumes that N=3 and obtains a strain energy function of the following form.

The Yeoh model can predict the mechanical behavior under large deformation well.For anisotropic muscle tissue, assuming that muscle fibers flex during compression along their direction and that the fibers are independent of each other,the specimen can be considered transversely homogeneous when loaded along the muscle fiber direction.Under quasi-static compression along the fiber direction, the experimental data fitting results of muscle tissue are shown in Fig.9.Where C10,C20,C30are the Yeoh hyperelastic constitutive model constants.According to the fitting result,C10= 0.00332, C20= 0.00754 and C30= 0.01643 are obtained.
Anisotropic materials can generally be viewed as continuous fibers distributed on an isotropic substrate.Some scholars use five tensor invariants to represent anisotropic hyperelastic strain energy density functions.
where I1,I2,I3are the fundamental invariants of the right deformation tensor, I4,I5are used to denote the anisotropy of the material.The expression for I4and I5are as follows:
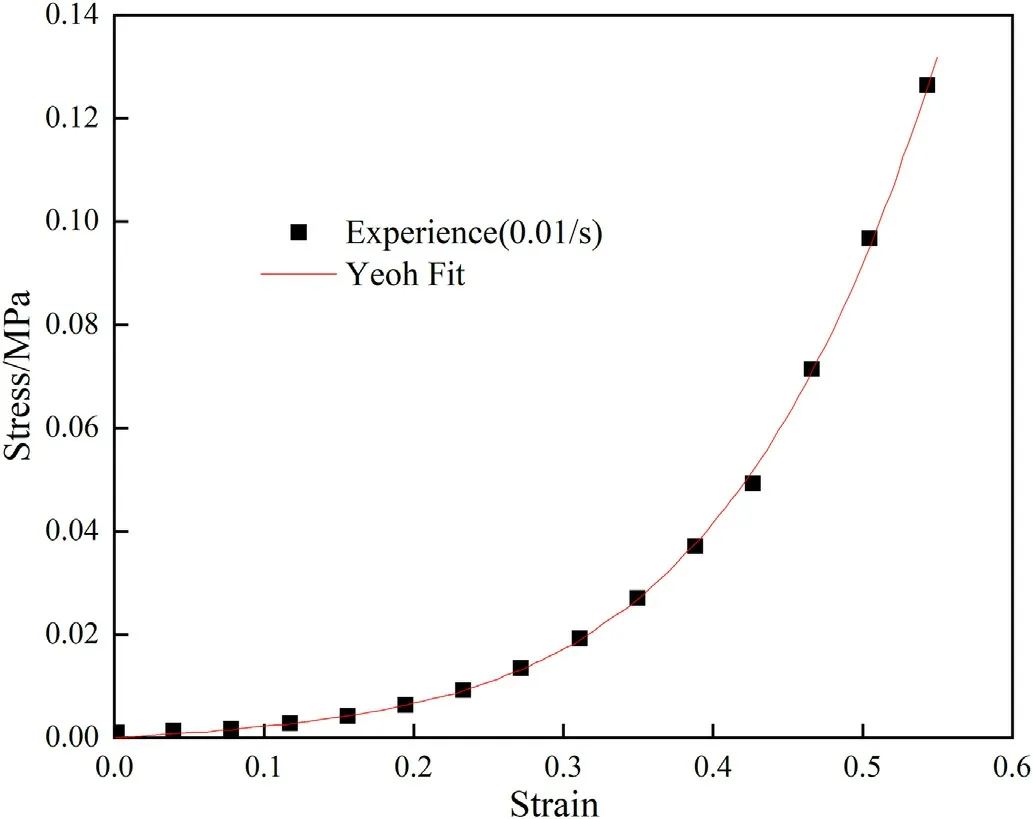
Fig.9.Quasi-static compression fitting curve parallel to the muscle fiber direction.
where N0= n0⊗n0, n0indicates the direction of the symmetry axis of the anisotropic material, C is the right Cauchy-Green deformation tensor,λFrepresents the deformation of the fiber.
The strain energy density function of anisotropic materials is usually divided into several different components as follows:
where W1expresses the strain energy of the isotropic matrix,which can be directly expressed using the isotropic constitutive model described in the above section; W2expresses the strain energy of the fiber itself.In muscle tissue, the fibers are very soft and can be considered unable to withstand compression,assuming that they flex during compression in the fiber direction, implying W2=0.However,this item needs to be considered when the fiber is stretched.

where G1and G2are the shear modulus parallel to and perpendicular to the fiber direction, respectively.When the loading condition is perpendicular loading,G1=0.Therefore,the stress in the muscle during perpendicular loading is as follows:
The fit to the perpendicular muscle fiber direction using quasistatic experimental data is shown in Fig.10.The parameter G2= 0.0027 MPa.The fitting result in Fig.10 is worse than that in Fig.9, because the experimental data of the compression experiment in the parallel fiber direction are first fitted and the parameters C10, C20, C30are determined.Therefore, when fitting the experimental data of the compression experiment in the perpendicular fiber direction, only the parameter G2can be changed, so there is an error between the experimental data and the fitting result in Fig.10.
6.2.Strain rate-dependent constitutive model
Soft materials often have a very pronounced strain rate effect,and the above constitutive model alone is not sufficient to describe this property.In order to obtain a strain-rate-dependent constitutive model, the constitutive model of the material is generally considered in two parts, as shown in the following equation:
where σerepresents the hyperelastic model at quasi-static, σvrepresents the viscoelastic model, which describes strain rate effects at high strains.The hyperelastic constitutive model described in the above section can be used to describe σe.The viscoelastic part of the incompressible isotropic material is expressed as follows:
where pvis the hydrostatic pressure, m(t-τ) is the relaxation function with the following expressions,F is deformation gradient tensor.

The σvused in incompressible anisotropic materials to represent the viscoelastic component is expressed as follows.
where φ is a tensor function,A(t-τ)is the relaxation function,F is deformation gradient tensor.

Fig.10.Quasi-static compression fitting curve perpendicular to the muscle fiber direction.
6.3.Muscle tissue strain rate-dependent constitutive model
According to the above theory, under the assumption of quasistatic loading as strain rate-independent, Wang [27] selected the Yeoh constitutive model in the hyperelastic part and proposed the constitutive models of compression along the muscle fiber direction and perpendicular to the muscle fiber direction, respectively.
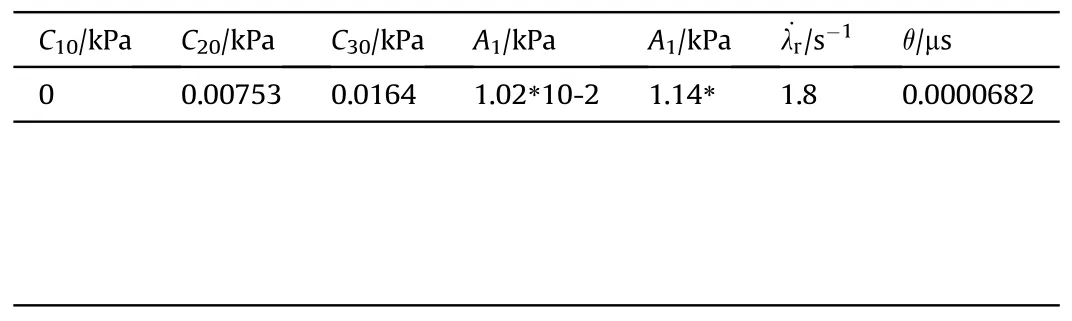
Table 1Parameters of the constitutive model loaded along the direction of muscle fibers.
It is interesting to note that the tensile and compressive constitutive models of muscle are significantly different.Wen et al.[28] used a modified Split Hopkinson Tension Bar to test the dynamic tensile performance of porcine muscles and established a dynamic tensile constitutive model along the direction of muscle fibers.The constitutive model is as follows:
Assuming a constant strain rate and a third-order Taylor expansion for the relaxation function, the viscoelastic term was integrated into a polynomial and then fitted using 1 stOpt to find the global optimum.The final fitted parameters of the experimental results for loading along the muscle fiber direction are shown in Table 1,and the fitted curves are shown in Fig.11.From the figure,it can be seen that fitting the experimental data for a strain rate of 2500/s, the intrinsic model curve also gradually diverges from the experimental data as the strain rate increases but still gives good results from the overall perspective.
The fitted parameters of the experimental results for loading perpendicular to the muscle fiber direction are shown in Table 2-Parameters of the constitutive model loaded in the perpendicular muscle fiber direction.The fitted curves are shown in Fig.12.It can be seen that by fitting the experimental data to the strain rate of 2500/s,the constitutive model curve can also overlap well with the experimental data as the strain rate increases.However, compared to the stress-strain curve along the muscle fiber direction,the stress-strain curve perpendicular to the muscle fiber direction is more evident in the pre-loading stress elevation,so in addition to the newly added parameters A6,the parameters A1were also re-fitted.The final fits all describe well the strain rate effects of each muscle tissue.
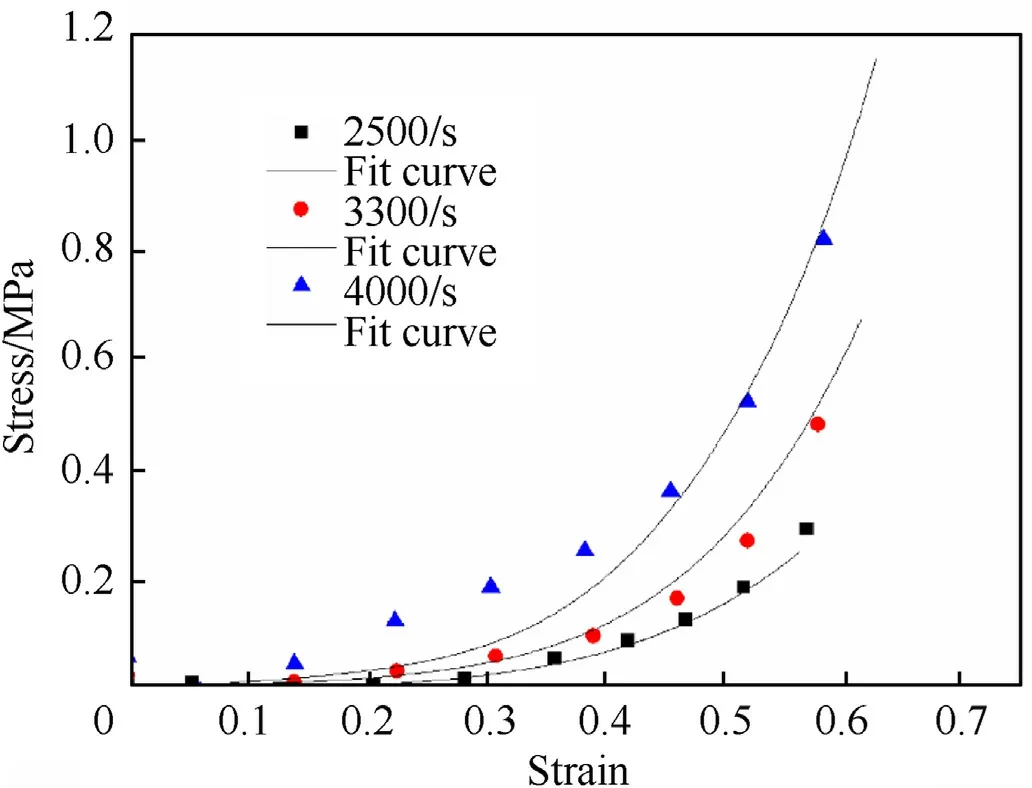
Fig.11.Fitting curves for loading along the muscle fiber direction at different strain rates.

Table 2Parameters of the constitutive model loaded in the perpendicular muscle fiber direction.

Fig.12.Fitting curves for perpendicular muscle fiber direction loading at different strain rates.
7.Conclusions
A modified SHPB apparatus was developed to investigate the dynamic compressive mechanical response of porcine muscle parallel and perpendicular to the fiber direction.A pair of PVDF force transducers were used to detect the contact force at both specimen-bar interfaces during an experiment.A circular cardboard pulse shaper was used to generate an initially slow loading profile in the incident pulse to ensure the muscle specimen deformed in a dynamic equilibrium state.To make the result more credible, the stress equilibrium process during loading was analyzed and the inertia-induced extra stress was corrected.The result shows that the porcine muscle is highly strain rate dependent in both directions from quasi-static to high strain rates.These dynamic responses are compared to existing dynamic data in the literature and are found to be in good agreement with them.Based on the mechanical response at different strain rates,an anisotropic constitutive model related to the strain rate of muscle tissue was developed.The experimental data were fitted using the constitutive model, and the overall fitting results were good.The availability of stress-strain data for porcine muscle tissue is expected to create an accurate strain-rate-dependent constitutive model to support numerical simulations in the future.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No.11872215), the National Defense Basic Scientific Research program of China (Grant No.JCKYS2019209C001) and the Fundamental Strengthening Program of the Military Science and Technology Commission Technical Field Foundation (2020-JCJQ-JJ-403).The authors thank Ben-yuan Xue and Hao Zheng of Nanjing University of Science and Technology for their help in conducting the experiments.
- Defence Technology的其它文章
- The dynamic response and damage models of rebar reinforced polymer slabs subjected to contact and near-field explosions
- Study of the axial density/impedance gradient composite long rod hypervelocity penetration into a four-layer Q345 target
- Active learning accelerated Monte-Carlo simulation based on the modified K-nearest neighbors algorithm and its application to reliability estimations
- Damage of a large-scale reinforced concrete wall caused by an explosively formed projectile (EFP)
- Air target recognition method against ISRJ for radio frequency proximity sensors using chaotic stream encryption
- New correlations for evaluating the equivalent bare charge mass for a cased charge

