Active learning accelerated Monte-Carlo simulation based on the modified K-nearest neighbors algorithm and its application to reliability estimations
Zhifeng Xu , Jiyin Co , Gng Zhng ,c,*, Xuyong Chen , Yushun Wu
a School of Civil Engineering and Architecture, Wuhan Institute of Technology, Wuhan, 430200, PR China
b School of Mechanical and Electrical Engineering, Wuhan Institute of Technology, Wuhan, 430200, PR China
c Failure Mechanics&Engineering Disaster Prevention and Mitigation,Key Laboratory of Sichuan Province,Sichuan University,Chengdu,610065,PR China
Keywords:Active learning Monte-carlo simulation K-nearest neighbors Reliability estimation Classification
ABSTRACT This paper proposes an active learning accelerated Monte-Carlo simulation method based on the modified K-nearest neighbors algorithm.The core idea of the proposed method is to judge whether or not the output of a random input point can be postulated through a classifier implemented through the modified K-nearest neighbors algorithm.Compared to other active learning methods resorting to experimental designs, the proposed method is characterized by employing Monte-Carlo simulation for sampling inputs and saving a large portion of the actual evaluations of outputs through an accurate classification, which is applicable for most structural reliability estimation problems.Moreover, the validity,efficiency,and accuracy of the proposed method are demonstrated numerically.In addition,the optimal value of K that maximizes the computational efficiency is studied.Finally,the proposed method is applied to the reliability estimation of the carbon fiber reinforced silicon carbide composite specimens subjected to random displacements, which further validates its practicability.
1.Introduction
New materials, such as alloys, ceramics, matrix composites,phase change materials, reactive materials, etc., have been widely used in aerospace and defense industries, whose varied applications cover infrastructure, aircraft wings and fuselages, armor,biomedical implants, microelectromechanical systems, etc.[1-4].In order to better guarantee military products’ quality as well as personnel’s life safety, reliability-based design has become the prevailing design method of various military equipment, which usually requires an extremely low failure risk, e.g., a failure probability on the order of 10-6[5-9].Evidently, direct experimental tests are banned for probing such a low failure risk because of the corresponding unaffordable cost.To handle such a problem, two general approaches are usually adopted:probabilistic methods and statistical methods [5,10].
Probabilistic methods resort to mechanics-based analytical models to predict failure probability,whose advantage is the ability to produce an entire reliability distribution using a relatively small amount of data.On the other hand, probabilistic methods are limited to simple failure mechanisms and simple probabilistic models, e.g., the bundle model for ductile structures [11], the weakest-link models for brittle and quasi-brittle structures [12],the fishnet model for lamellar materials [13],etc.Recently,Xu and Le proposed the first passage model based on random fields[14,15],which is a continuous model intended for describing the failure statistics of complex structures.
On the other hand,statistical methods are anchored by Monte-Carlo (MC) simulations, which are usually computationally more expensive than probabilistic methods.But the ability to deal with sophisticated structural configurations and diverse failure mechanisms makes statistical methods more beneficial for practical engineering problems than probabilistic methods [16].Since direct MC simulations are universal but cumbersome, numerous approaches aimed at improving the computational efficiency have been developed [5], such as importance samplings [17,18],directional samplings [19,20], subset simulations [21,22], Latin hyperrectangle samplings [23,24], response surface methods [25],directional division-based methods [26,27], etc.
In recent years, machine learning-based statistical methods[28-32] have found their superiorities to classical statistical methods on structural reliability estimations for having better computational efficiency,in which the heuristic ones are gradientbased algorithms [33,34], swarm algorithm-based methods[35-37], genetic algorithms-based methods [38-40], active learning-based methods [32,41,42], deep learning-based methods[43], etc.In terms of machine learning, reliability estimation falls into the classification problems, aiming at providing accurate predictions on random input points’ being in the safe domain or not.However, misclassifications produced by the machine learning processes would deteriorate the accuracy of these methods,which would yield considerable errors for reliability estimations when the failure probability is sufficiently low.
Aiming at decreasing misclassifications and therefore increasing the accuracy of reliability estimations,this paper proposes an active learning-based statistical method based on the modified K-nearest neighbors (KNN) algorithm, in which the convex hull of nearest neighbors is used for improving the accuracy of classifications.Rather than regulating the sampling points through experimental design as in other active learning methods, the proposed method uses MC simulations for sampling the input points.The core idea of the proposed method is to use the modified KNN algorithm to determine whether or not a random point can be postulated or needs to be actually sampled by MC simulations.Through such an implementation, a large number of evaluations of the corresponding outputs can be saved, resulting in a satisfactory acceleration.At this point, it is noted that, since the chance of its misclassifications is low, the proposed method can be applied to accelerate most MC simulations with sufficient accuracy, which is in a sense general for reliability-related problems.Evidently, the proposed method can be combined with any method that requires MC simulations, giving birth to new methods with better efficiencies.
The rest of the paper is organized as follows:Section 2 presents the necessary theoretical background of the proposed; Section 3 presents and validifies the proposed acceleration method for MC simulations; Section 4 studies the optimal value of K that maximizes the computational efficiency;Section 5 applies the proposed method to the reliability estimation of the carbon fiber reinforced silicon carbide composite specimens subjected to random tensile displacements, from which the practicability of the proposed method is further verified.
2.Theoretical background
This section presents the necessary theoretical background for this paper,in which Subsection 2.1 introduces the fundamentals of reliability analysis, and Subsection 2.2 demonstrates the KNN algorithm.
2.1.Reliability analysis
Given a structure subjected to n number of random variables denoted by the vector x = [x1, x2, …, xn]T, and a set of nominal responses {y1(x), y2(x), …, yj(x)}, where yi(x) < 0 represents a corresponding failure state and the superscript T is the transpose operator.The following performance function is defined as the measure of the structural state
where y>0 or y<0 indicates the structure is in the safe or failure state, respectively.If the existence of any negative nominal response can trigger the structural failure, then y = min {y1(x),y2(x), …, yj(x)} becomes the performance function of the entire structure.
Conventionally, x and y are usually referred to as the input and output, respectively.Besides, the input x is called positive or negative according to the sign of its output y, i.e., x is positive if y>0,x is negative if y<0.It is noted that x can be a combination of loads and resistances.The limit between the safe state and the failure state is represented by the following limit state function
Evidently, the failure probability becomes
where fx(x1,x2,…,xn)is the joint probability density function(PDF)of each xi, and Ωs= {x| y(x) > 0} is the safe domain, and R is the reliability.
Through MC simulation, a input set X = {x1; x2; …; xN} can be generated,in which N is the sample size,and xi=[x1i,x2i,…,xni]Tis the ith sample input.The output set with respect to X is represented by the output set Y={y1;y2;…;yN},where yi=y(xi).According to the law of large numbers, the failure probability can be computed by
where NSis the total number sample points in Ωs.
2.2.The K-nearest neighbors algorithm
As one of the most widely used classifiers in machine learning,the KNN algorithm can be applied to the classification of reliability problems,in which a sample point should be classified into the safe domain or the failure domain by judging its p-value,i.e.,if p>0.5,the point is classified into the safe domain;else,it is classified into the failure domain.And the p-value is computed by
where K is the number of neighbors, and Ksis the number of neighbor sample points that belong to the safe domain.It is noted that K can be a prescribed constant or a random variable, e.g., the number of sample points whose distances to the point of interest is smaller than a critical distance,where the distance metrics used in KNN can be Euclidean distance, Minkowski distance, Manhattan distance, Chebychev distance, correlation, etc.
3.Active learning accelerated Monte-Carlo simulation method based on the modified K-nearest neighbors algorithm
This section presents the active learning accelerated Monte-Carlo simulation method, which employs the modified KNN algorithm as the classifier for determining whether the output of a random input point can be postulated or not,in which Subsection 3.1 presents the method, Subsection 3.2 numerically validates the method, and Subsection 3.3 studies the optimal value of K numerically.
3.1.Method presentation
The proposed acceleration method for Monte-Carlo simulations is anchored by postulating the sampling result through the modified KNN algorithm.To be more specific, for the i-th input xi, the modified KNN algorithm will work as a classifier that determines whether the output of xican be postulated.In this case, the corresponding output is estimated by yi= y*(xi), where y* is the estimator; otherwise, the output is obtained by evaluating the performance function in Eq.(1), i.e., yi= y (xi).In conventions of machine learning,the evaluation of yithrough y(xi)is referred to as the i-th experiment.At this point, the following convention is made: inputs whose outputs are postulated through the proposed method are referred to as postulates, and postulates whose sign is contradictory to the corresponding experiments are referred to as misclassifications.
Fig.1 shows the flowchart of the proposed method, which can be concluded into the following steps:Step 1,determine the sample size N and the number of neighbors K;Step 2,sample K number of random inputs and evaluate their corresponding outputs; Step 3,perform Step 4 and Step 5 until the number of currently sampled inputs reaches N; Step 4, sample a random input and determine whether it can be postulated through the modified KNN algorithm;Step 5, if the input sampled in Step 4 can be postulated, then estimate the output through interpolation, else evaluate the performance function.
The classifier implemented through the modified KNN algorithm contains the following four steps: Step 1, find the K nearest neighbors of the i-th input xi,which are denoted by xi1,…xiK;Step 2,if xi1, …xiKare uniformly positive or negative,then perform Step 3 and Step 4,else,conclude that x cannot be postulated;Step 3,hatch the convex hull of xi1, …xiK; Step 4, if xiis inside the convex hull,then estimate the output of xiby yi= y*(xi), if xiis outside the convex hull, then conclude that x cannot be postulated.Fig.2(a)presents the flowchart of the modified KNN algorithm, while Fig.2(b) demonstrates the corresponding classification details.Nevertheless, this classifier would still produce misclassifications for the following cases (as shown in Fig.2(c)): (1) the limit state surface has large curvatures; (2) the limit state surface contains multiple pores;and(3)the limit state surfaces are closely adjacent.Yet the above-listed cases for misclassifications are usually rarely encountered in structural reliability assessments.Hence, the proposed classifier is expected to yield accurate classification results and therefore can be safely applied to accelerate most Monte-Carlo simulations for structural reliability estimation.
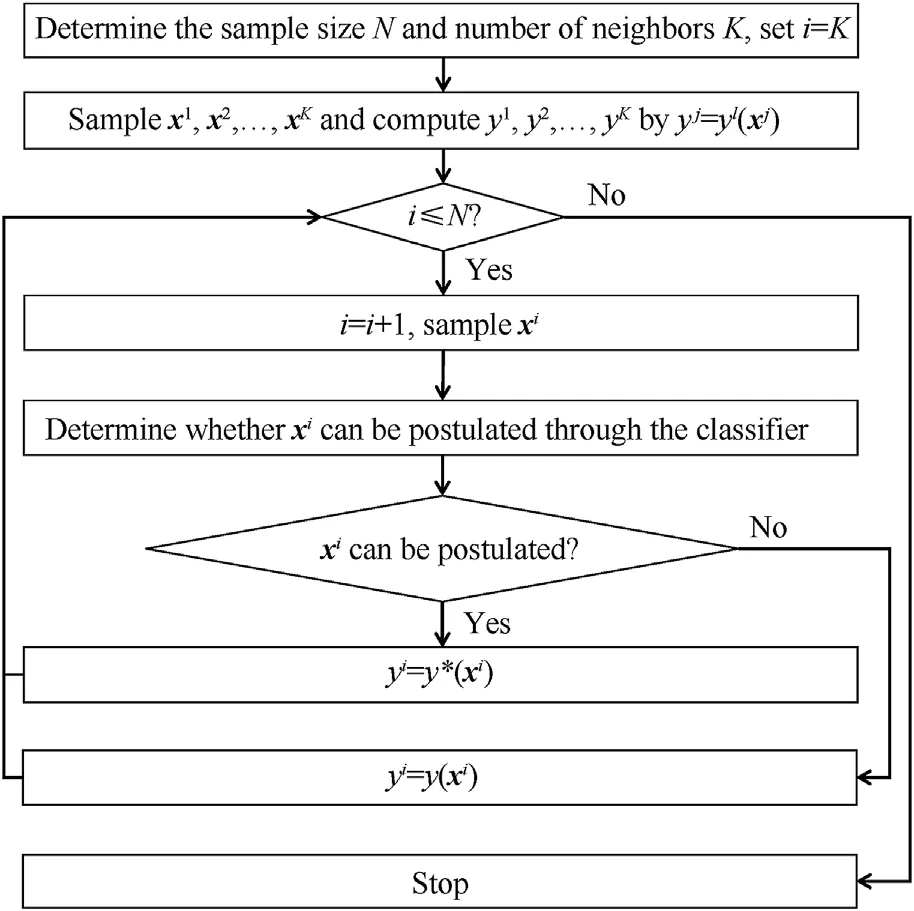
Fig.1.Flowchart of the the proposed method.
In the proposed method, the estimator is chosen to be the following interpolation function

3.2.Numerical validation
First of all, since the proposed method is designed to be a universal acceleration method for most MC simulations for reliability estimations, this subsection only studies the acceleration effect of the proposed method, while the comparison with other reliability estimation methods is not necessary.Moreover, the proposed method is applicable to most reliability estimation methods that require MC simulations, further improving their efficiency.
In order to validate its accuracy and efficiency, the proposed method is used to accelerate the reliability estimation of the following modified version of the series system reliability problem with high non-linearity [43].
in which x1and x2obey standard Gaussian distribution.

Fig.2.Illustration on the modified KNN algorithm: (a) The flowchart; (b) The demonstration of the classification; (c) The missclassification cases.

Fig.3.The numerical validation result: (a) Experiments and postulates; (b) Postulates; (c) Experiments.
Fig.3 shows the numerical simulation result using the proposed method, in which (a) shows the simulation result of both experiments and postulates,(b)shows the simulation result of postulates,and (c) shows the simulation result of experiments.In this numerical validation,the value of K is set to 50,and the interpolation method adopted is triangulation-based linear interpolation.A total of 105input points are sampled,232 of which are negative,and the corresponding estimated failure probability is 0.232%, while the exact value is 0.226%.Table 1 shows the statistics of the numerical simulation result using the proposed method, in which 99,212 out of the 105inputs are postulated using the proposed method.As a result, the proposed method can save 99.212% of the MC simulations, which accelerated the direct MC about 126 times.And the number of misclassifications is zero.The mean and standard deviation of the postulate errors are-0.0254 and 0.1389,respectively.Fig.4 shows the histogram of the postulate errors,which indicates the proposed method also has good accuracy for estimating the performance function.Since the correct classification between positive inputs and negative inputs is crucial for reliability computation while the postulate errors are relatively trivial, it is concluded that the proposed method is surprisingly accurate and suitable for reliability estimations.
3.3.Study on the optimal value of K
This section analyzes the optimal value of K, which maximizesthe computational efficiency by minimizing the number of experiments.It is noted that the optimal value of K is influenced by the dimension of inputs.In order to numerically investigate the optimal value of K, the following two cases are studied: Case 1 uses the modified version of the series system reliability problem with high non-linearity as the performance function(represented by Eq.(8)),where the exact failure probability Pf= 0.226%; Case 2 is the following high-dimensional problem [32].

Table 1The statistics of the numerical simulation result using the proposed method.
where x1to xnobey the identical lognormal distribution with a unit mean and a standard deviation σ=0.2,n=40,and the exact failure probability Pf= 0.196%.
The simulation results for the number of experiments and misclassifications for the above cases are shown in Table 2, and Table 3, respectively, and from Table 3, it can be seen that the proposed algorithm is amazingly accurate by producing exactly zero misclassifications for all the tested cases.Fig.5 show the corresponding number of experiments as a function of K with respect to different sample sizes, in which the number of experiments is plotted in log form.Besides, the successful application of the proposed method to Case 2 demonstrates its applicability to highdimensional cases.Furthermore, it can be seen from Fig.5 that:1), for a given sample size, the number of experiments would first decrease as K increases and then increase as K increases,indicating there exists an optimal value of K that minimizes the number of experiments;2),the optimal value of K is influenced by the sample size and the dimensionality; and 3), after K passes the corresponding optimal value, the increasing rate of the total number of experiments becomes low, implying K can be moderately greater than the corresponding optimal value in practice.
4.Application to the reliability estimation of carbon fiber reinforced silicon carbide composite specimens
In this section,the proposed method is applied to the reliability estimation of the carbon fiber reinforced silicon carbide (C/SiC)composite specimens under random tensile displacements.The studied specimens are representative volume elements(RVEs)that consist of C/SiC T700-12 K unidirectional ceramic matrix composite fibers.As shown in Fig.6(a), each RVE contains 10 fibers with random tensile strengths, in which the fibers are modeled as 2-dimensional rectangular elements.One side of the sample is clamped while the other side is subjected to random tensile displacements denoted by u.The length, width, and thickness of a fiber are 1000 μm,10 μm, and 10 μm, respectively, and u obey the normal distribution, whose mean are standard deviation are 4 μm and 0.4 μm, respectively.The material constitutive model for the fibers is chosen as the isotropic damage model with linear softening (shown in Fig.6(b)) [44], whose material parameters are described by Table 4.OOFEM [45], which is an open-source finite element analysis program,is applied for performing the simulation.For any RVE, failure or safety is characterized by whether there exists a fiber whose damage parameter is greater than 0.5, and Fig.6(c) shows the damage pattern of one realization that failed during the finite element simulation.
Altogether,105samples are tested, in which each run has 200 sub-steps.The number of failed RVEs is 26,which corresponds to a failure probability equals 0.026%.Among the 105outputs,only 2771 of them are obtained experimentally, while the rest 97,229 are postulated.Therefore,the proposed method saved 97.2%of the total MC simulations,accelerating the direct MC simulations by about 35 times.In order to further validate the misclassification error,1000 postulates are selected randomly, whose outputs are evaluated experimentally.It is found that the corresponding number of misclassifications is zero, demonstrating the good classification accuracy of the proposed method.

Table 2The statistics of the total number of experiments using the proposed method.
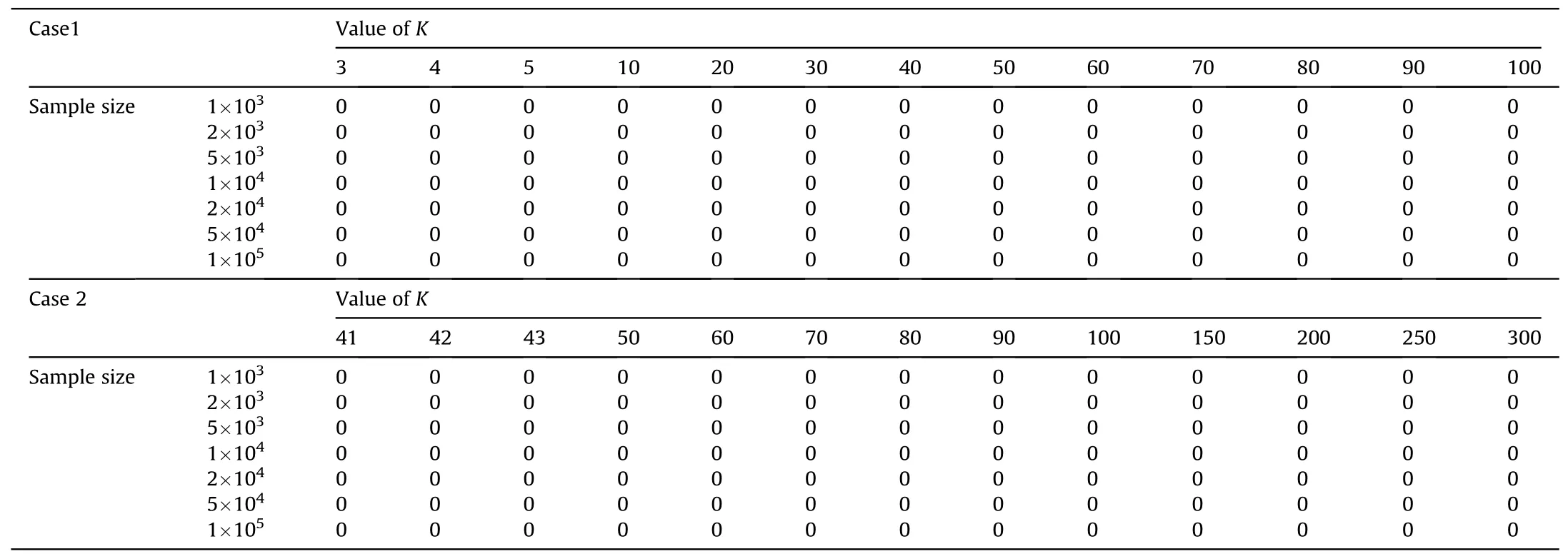
Table 3The statistics of the total number of misclassifications using the proposed method.

Fig.5.Number of experiments VS the value of K: (a) Case 1; (b) Case 2.

Fig.6.Demonstration of the finite element simulations: (a) Configurations and loadings; (b) Implemented stress-strain diagram; (c) Dammage parttern of a failed realization.

Table 4Material parameters of the fibers.
5.Conclusions
This research proposes an active learning-based method for accelerating Monte-Carlo simulations in structural reliabilityrelated problems, whose chance of misclassification is proven to be extremely low.In addition, the optimal value of K that maximizes the computational efficiency is studied numerically.Finally,the application to the reliability estimation of the C/SiC composite specimens validates the practicality of the proposed method.Moreover, the following conclusions are drawn:
(1) The modified KNN algorithm using nearest neighbors’convex hull can accurately classify a random input into the safe domain or the failure domain;
(2) Using triangulation-based interpolations yields estimated outputs with reasonable errors;
(3) There exists an optimal value of K for the proposed method that minimizes the number of experiments;
(4) The proposed method is applicable to high-dimensional cases.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No.12002246 and No.52178301),Knowledge Innovation Program of Wuhan (Grant No.2022010801020357), the Science Research Foundation of Wuhan Institute of Technology (Grant No.K2021030), 2020 annual Open Fund of Failure Mechanics & Engineering Disaster Prevention and Mitigation, Key Laboratory of Sichuan Province (Sichuan University)(Grant No.2020JDS0022),and Open Research Fund Program of Hubei Provincial Key Laboratory of Chemical Equipment Intensification and Intrinsic Safety (Grant No.2019KA03).
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors wish to acknowledge the financial supports provided by the National Natural Science Foundation of China (Grant No.12002246 and No.52178301),the Science Research Foundation of Wuhan Institute of Technology (Grant No.K2021030), 2020 annual Open Fund of Failure Mechanics & Engineering Disaster Prevention and Mitigation, Key Laboratory of Sichuan Province(Sichuan University)(Grant No.2020JDS0022),and Open Research Fund Program of Hubei Provincial Key Laboratory of Chemical Equipment Intensification and Intrinsic Safety (Grant No.2019KA03).
- Defence Technology的其它文章
- Eigen value analysis of composite hollow shafts using modified EMBT formulation considering the shear deformation along the thickness direction
- Synthesis of energetic coordination polymers based on 4-nitropyrazole by solid-melt crystallization in non-ionization condition
- RDX crystals with high sphericity prepared by resonance acoustic mixing assisted solvent etching technology
- Study of residual stresses and distortions from the Ti6Al4V based thinwalled geometries built using LPBF process
- Modeling and simulation of solvent behavior and temperature distribution within long stick propellants with large web thickness undergoing drying
- Assessment of the ballistic response of honeycomb sandwich structures subjected to offset and normal impact

