组合匝道瓶颈下交通流相变研究
胡河森, 靳文舟
(华南理工大学土木与交通学院, 广东广州510641)
0 引言
许多交通学者通过对不同国家高速公路交通的观察发现,在最开始的交通自由流中出现的拥堵现象都与车辆速度的突然下降或者密度的突然上升有关[1-2]。这种拥堵现象主要发生在高速公路的瓶颈处,尤其是在入口匝道瓶颈处,这一现象引起了众多科学家的关注。
交通学者首先基于以往的基本图微观和宏观模型,试图对这一现象进行描述[3-8]。由此产生的一系列高速公路交通数学理论和模型,通过对自由流的不稳定性来解释自由流中发生的拥堵现象,这种不稳定性产生于高速公路上足够大的车流并导致出现了移动堵塞。在入口匝道瓶颈处,当来自瓶颈上游的车流量足够大并且入口匝道的流量逐渐上升时,自由流中就会发生移动堵塞现象,然而,这些模型的结果表明的“自由流中的拥堵与自发的移动堵塞出现有关”这一结论与实际的观测结果之间存在严重冲突。
著名的交通科学家Kerner引入了三相交通流理论,不同于以往的交通流相位划分,在该理论中,存在3个不同的交通阶段:自由流相、同步流相和宽运动堵塞相[9]。Kerner指出在堵塞出现之前,流量密度空间中存在着一个复杂的二维散布区域,即同步流,也就是说,堵塞不会在自由流中自发出现,而是出现在同步流的相变中,在此之前,自由流到同步流的相变会更早发生(简称F→S相变)[10]。此后,基于三相交通流理论,国内外众多学者借助元胞自动机模型考察了交通流状态演化的复杂性和多变性[11-16]。这些模型都是从微观仿真层面对交通流相变进行研究,无法从宏观层面对交通流整体的特性进行描述。
在中观层面上(结合了微观和宏观的特性),车流表现出的许多特性,特别是其存在的相变形成和相变转换现象在物理系统中广泛存在,因此交通流物理学引起了众多学者的关注。而用于对不同性质的复杂系统的一阶相变进行描述的统计物理中的概率主方程无疑是一个重要的方法[17]。主方程方法是针对车辆集群(一组具有共同特定性质的车辆)大小的随机波动概率来研究相变特性,即车辆集群的形成和演化。基于主方程的交通流中的相变模型首先由Kühne等[18-19]、Mahnke等[20]提出,他们的基本假设为在非匀质的道路上会出现一个预集群,其增长导致了交通拥堵,然而,这与实际中观测到现象并不相符,实际上Mahnke和Kühne等提出模型更接近于描述自由流到宽运动堵塞的相变(F→J相变)。正如Kerner提出的微观模型所说,真实的交通拥堵应该发生在F→S相变中。
上述所描述的瓶颈处相变模型都只讨论了单个瓶颈,如单个入口匝道瓶颈,然而在实际生活中,城市道路中的瓶颈更为复杂,其中不乏许多组合瓶颈[21-25]。组合瓶颈不仅影响交通畅通,还会引发更为复杂的交通现象,并且组合瓶颈之间存在着强烈的相互作用这一特性完全不同于单个瓶颈。此外,对于组合瓶颈最初的空间非均匀自由流动,相关的相变模型和概率理论研究较少,结构非均匀性对于统计物理学的许多其他非粒子系统中的相变也起着非常重要的作用,因此,基于概率论主方程和三相交通流理论,本文研究了具有连续入口-出口匝道瓶颈的相互作用引起的交通拥堵现象。
1 基于三相交通流理论分析瓶颈处的交通流相变特性
1.1 瓶颈处的永久性速度扰动

(1)
将位于瓶颈处的这种局部扰动称为是瓶颈处的确定性扰动。这种瓶颈处的永久非匀质性,导致即使在没有随机扰动的情况下,瓶颈处的车辆集群也存在,称这部分集群为确定性车辆集群。
1.2 瓶颈处交通拥堵具有概率性
Shiomi等[26]发现在给定的流量下瓶颈处交通拥堵的概率是一个随流量变化的递增函数。由此可见,瓶颈处的交通拥堵具有概率性,可以采用基于三相交通流理论来描述瓶颈处的这种概率特性。
①速度适应效应。
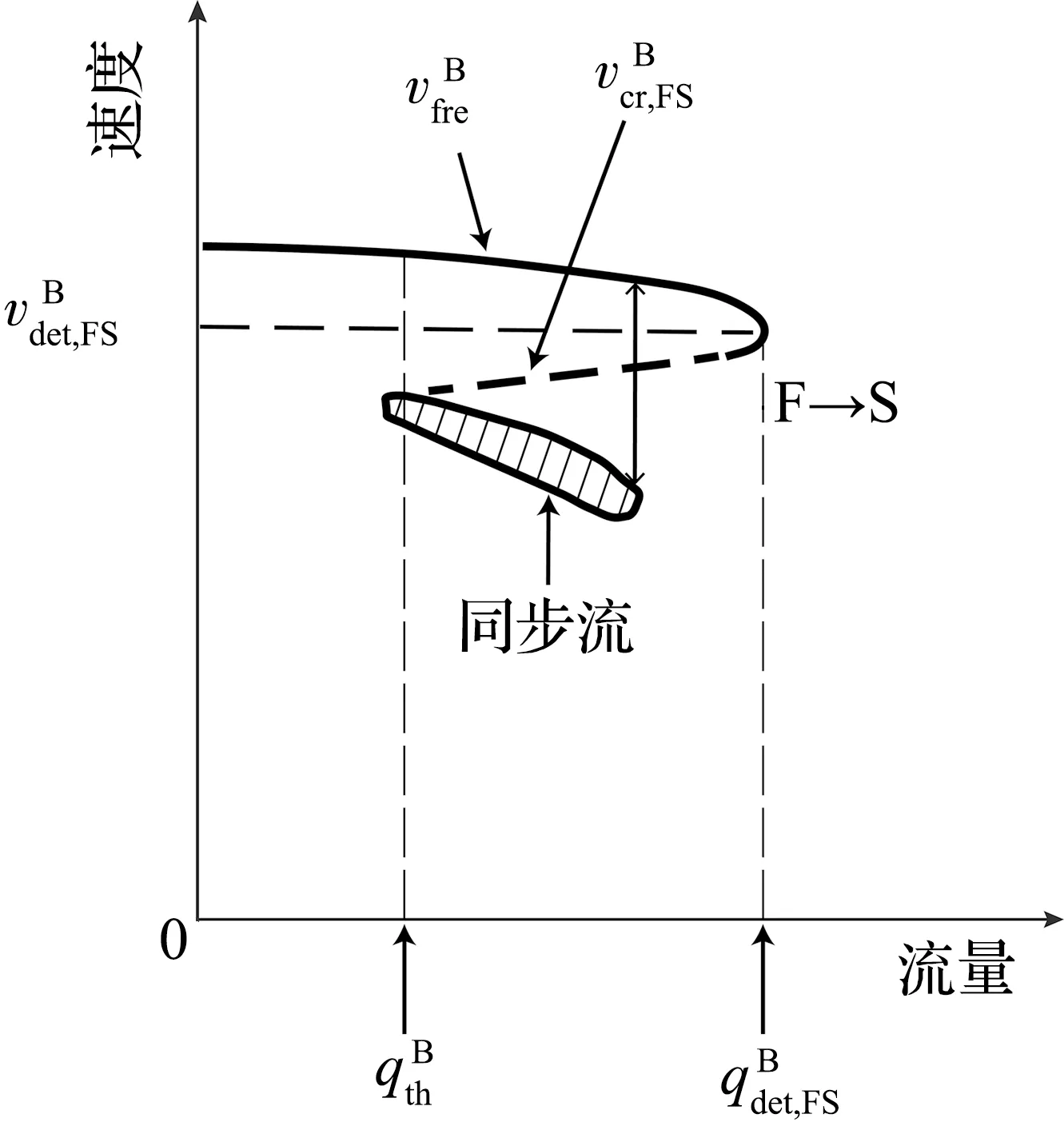
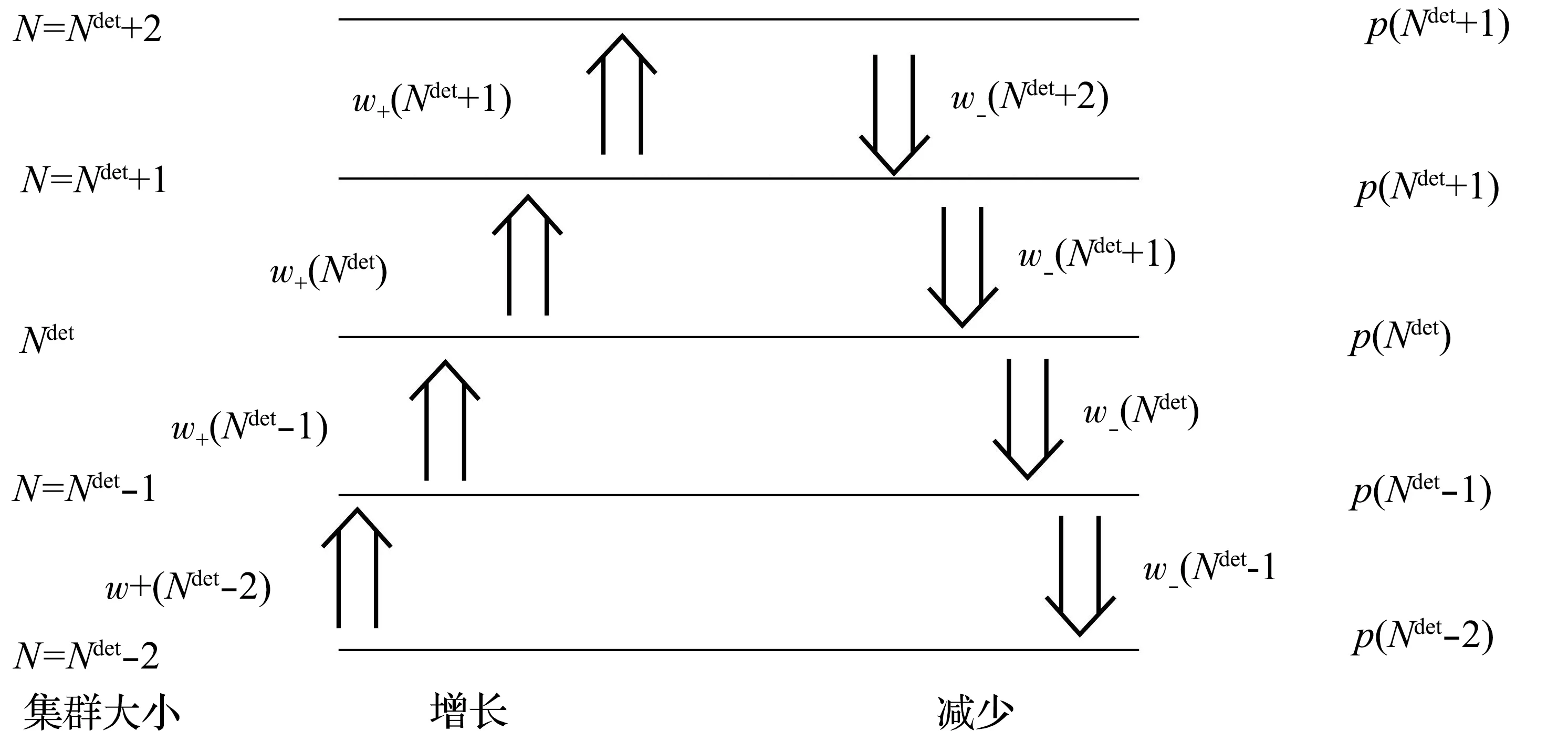
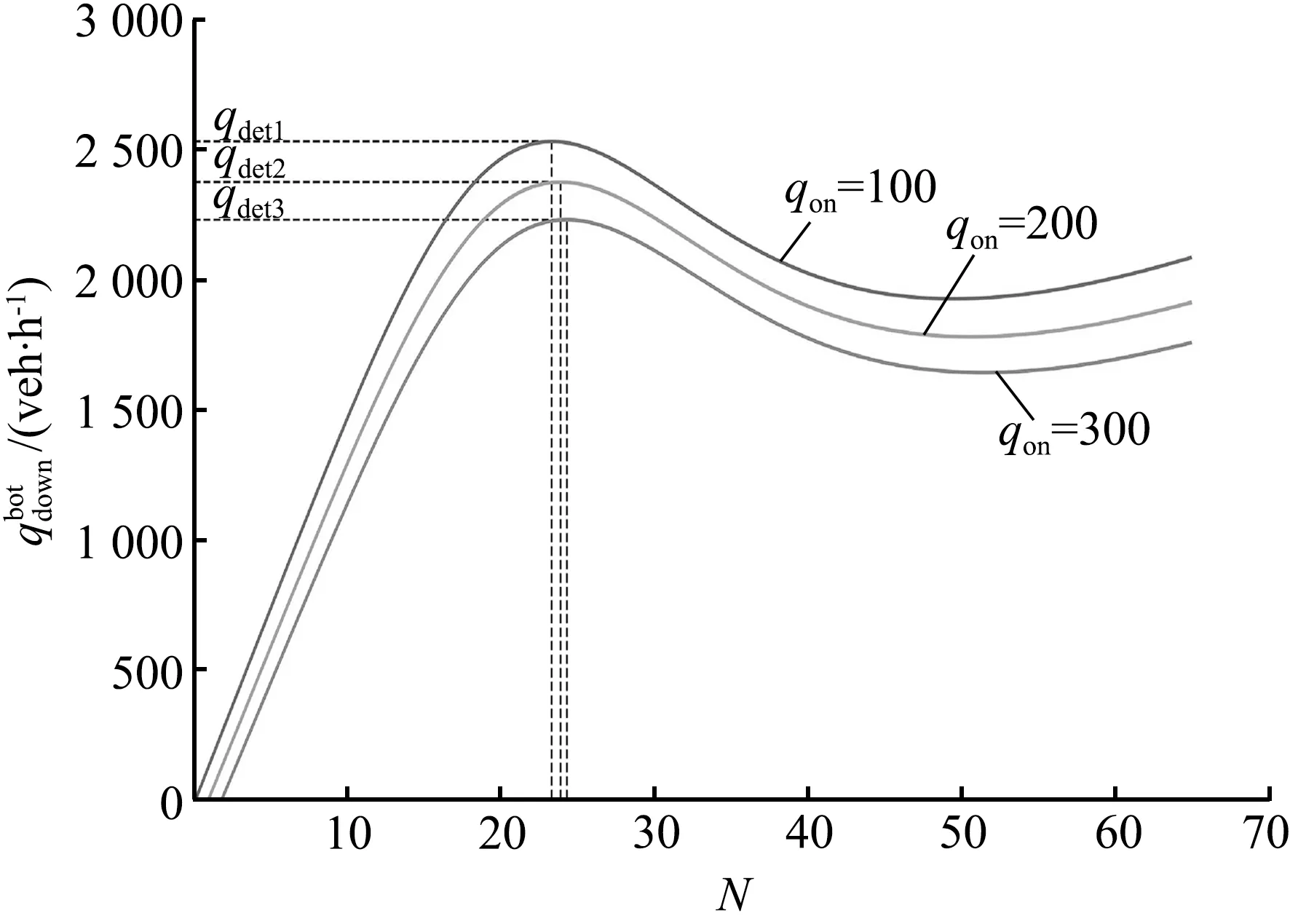
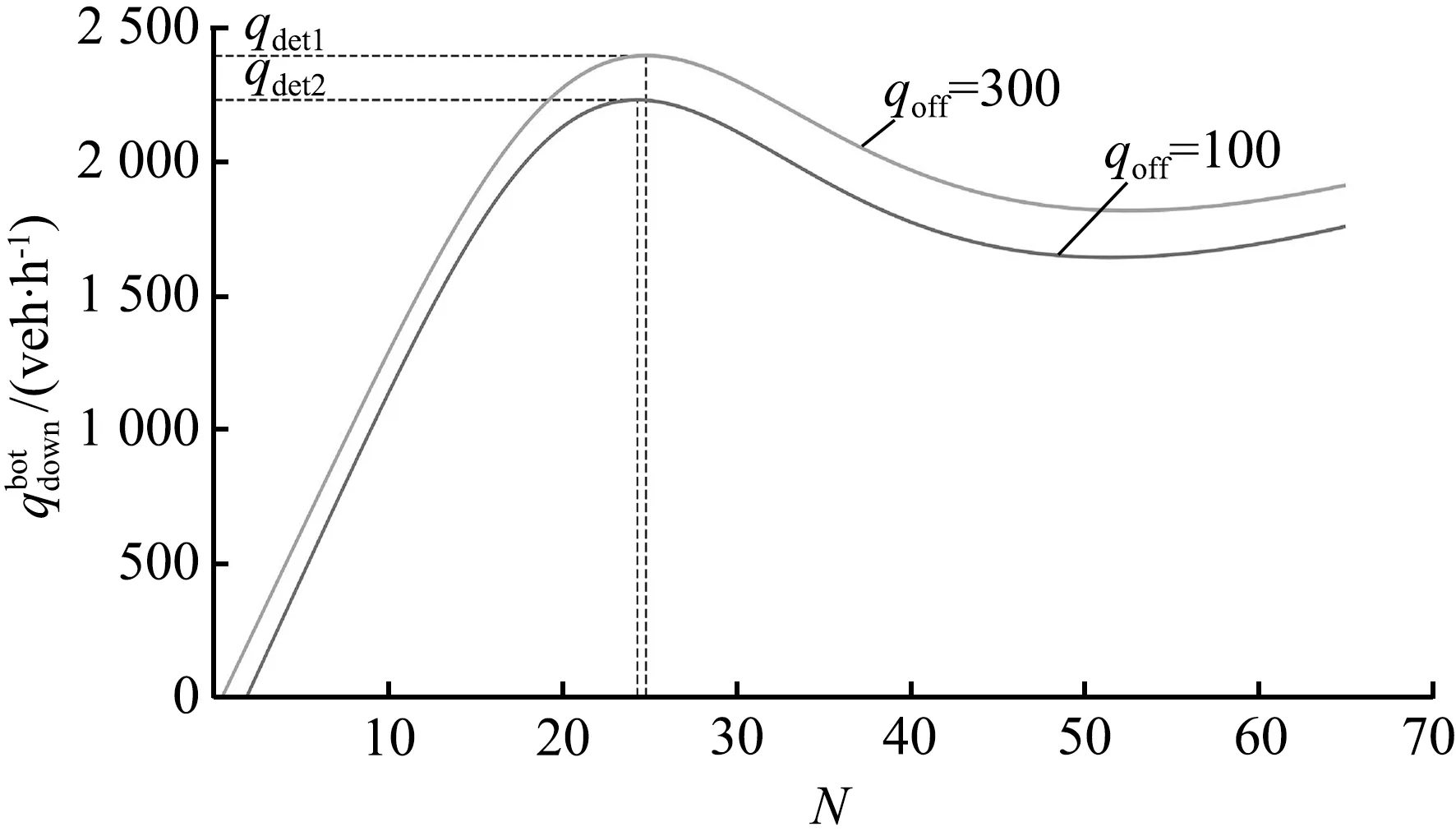
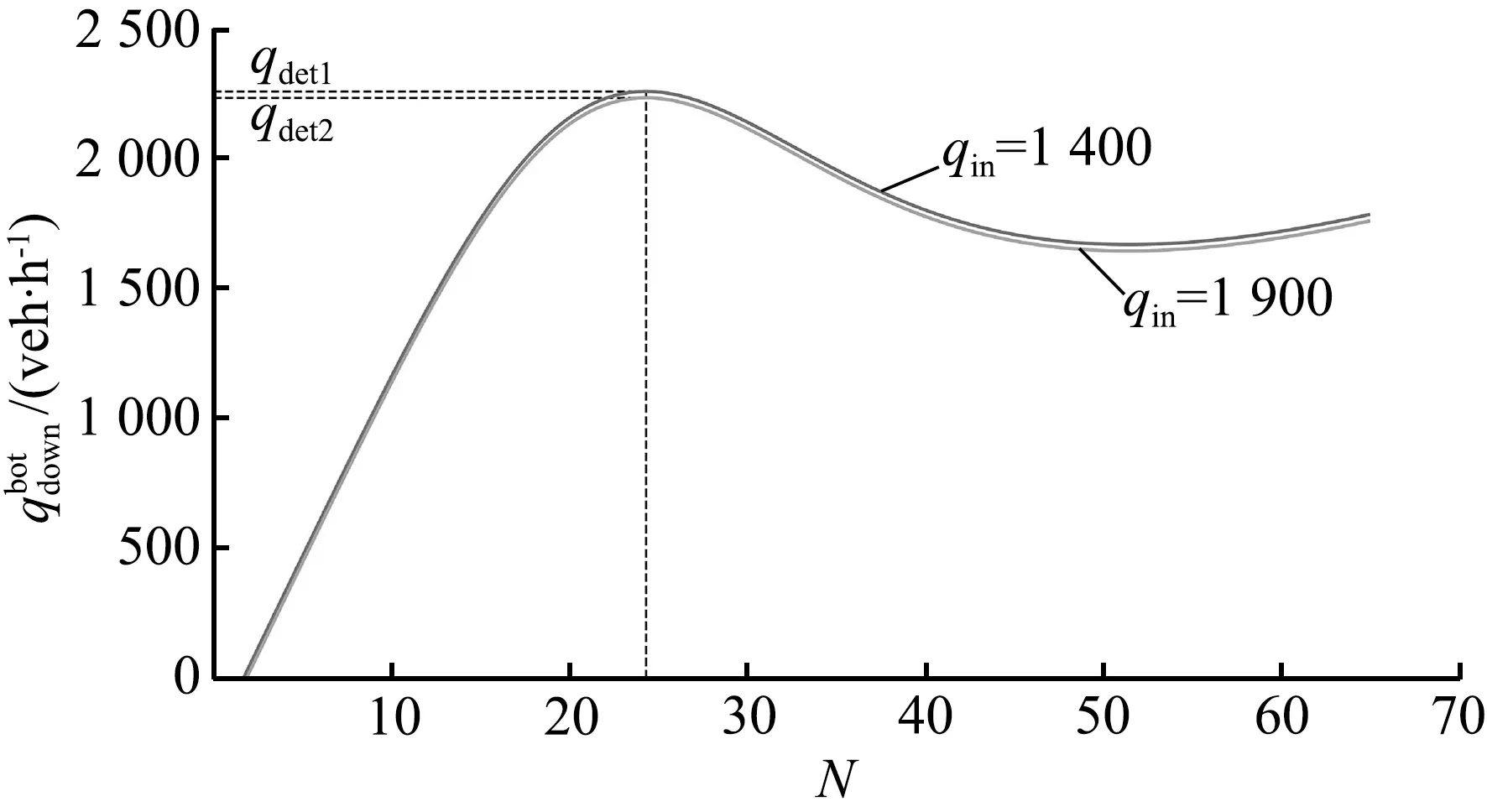
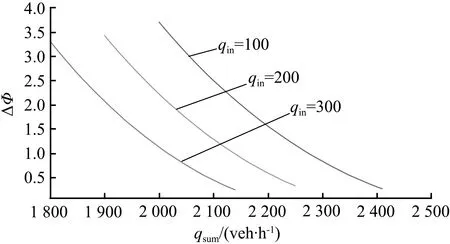
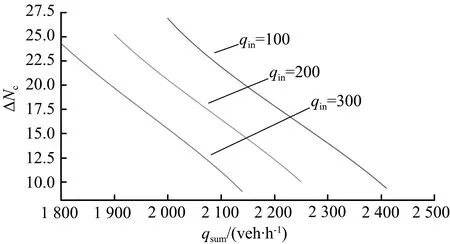
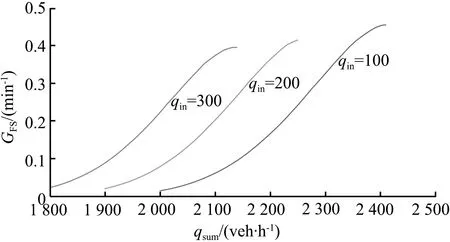
在三相交通流的跟驰规则中,动态同步车头间距G和动态安全间距gsaf与当前车速度v和前车速度vτ相关,即G=G(v,vτ)和gsaf=gsaf(v,vτ)。定义车辆和前一车辆之间的车头间距为g,在g>G(v,vτ)时,车辆加速;当g gsaf(v,vτ)≤g≤G(v,vτ)。 (2) 速度适应效应通常导致车辆减速,从而交通流趋向于同步流。 ②过加速效应。 在满足公式(2)时,车辆跟车,然而在前车没有加速且车辆速度不比当前车慢时,车辆也可以加速。这种车辆加速过程被称为车辆过加速。过加速效应的定义为:驾驶员的过加速动机导致了满足公式(2)时的低速度跟车车流中出现较高速度车流。过加速效应相关的车辆加速导致了交通流趋向于初始的自由流。 过加速效应表现为驾驶员加速超车的可能意愿。用POA(probability of over-acceleration)表示过加速效应的概率,等于跟驰车辆中的超车概率P。 在给定的车流密度下,自由流中的超车概率大于同步流中的超车概率。此外,P和过加速概率POA表现出不连续的特征,这些概率-密度函数可以用Z形函数定性表示(如图1所示)。 图1 超车概率和过加速概率的密度函数曲线Fig.1 Density function curve of probabilities of passing and over-acceleration probability 概率-密度的定性Z形函数表明在F→S标记的密度范围内的初始自由流中的任何密度都可能发生交通拥堵。由此可见,初始自由中存在2种相反趋势之间的竞争——由过加速效应导致的自由流趋势和由速度适应效应导致的同步流趋势。只要过加速效应强于速度适应效应,那么就能保持自由流状态,然而,随着密度增大,POA就会减小,即过加速效应减弱,则初始自由流将趋向于同步流。 同时,即使道路上不存在瓶颈,在这种情况下过加速效应和速度适应效的自由竞争依然存在,此时F→S相变仍然会发生,只不过这种情况下相变发生的概率要比瓶颈附近发生相变的概率要小得多。 为了更好地分析交通拥堵的相变特性,结合Kerner在三相交通流中提出的Z形速度-流量函数和S形密度-流量函数[8],三相交通流相变定性曲线如图2所示。 (a) 速度-流量Z形曲线 (3) 同时,从图2可以看到,对于自由流中的流量qsum有一个范围: (4) 式中qsum为自由流中的流量,这也与概率-密度函数中的密度范围对应。 (5) F→S相变必然发生。 (6) 无论随机扰动多大,瓶颈处都不可能发生交通拥堵。 确定性扰动和随机扰动引起的瓶颈处确定性集群和随机集群的变化,最终导致发生交通拥堵或者维持初始自由流。接下来将借助概率论中的主方程模型研究实际交通中一类重要的组合瓶颈——连续入-出口匝道引起的交通拥堵现象 本文研究的是一个具有连续入-出口匝道的组合瓶颈道路,连续入-出口匝道瓶颈如图3所示。图3中,入口匝道在出口匝道的上游,主干道为单车道道路,不包含匝道过渡路段。qin为主干道流量,qon为入口匝道流入量,qoff为出口匝道流出量,qdown为瓶颈下游流出量,L为2个匝道之间的距离。 图3 连续入-出口匝道瓶颈 Fig.3 Continuous on-ramp and off-ramp bottleneck 不同于单个孤立匝道瓶颈,当道路上存在2个相距不远的交通瓶颈时[27],每个瓶颈不再独立地对交通流产生影响,而是在相互干扰下共同发挥作用,就形成了组合瓶颈效应。同时,假设集群的上游和下游出现同质自由交通流,确定性集群Ndet仅存在于2个匝道之间的路段。 组合瓶颈内的自由流的确定性扰动是由3个流量引起的:qon、qoff和qin。qon和qin在组合瓶颈内的道路区域合并。进入扰动范围内的总流量为 qsum=qon+qin。 (7) 除开存在组合瓶颈效应外,单个匝道也对其附近的车流产生影响。由于本文研究连续入-出口匝道形成的组合瓶颈相变,因此假设组合瓶颈内的扰动是连续平均的 。 考虑位于组合瓶颈之间的集群内的车辆总数N的动态变化,与Ndet相比,集群内的车辆总数N可以随时间的变化随机增长或减少,同时假设每一时刻集群内只发生一辆车的变化,如图4所示。 图4 由初始扰动引起的车辆集群变换Fig.4 Vehicle cluster conversion due to initial disturbance 提出如下主方程模型: (8) (9) 边界条件为 w-(0)=0, (10) 并且假设w-满足w-≥0。可以看到,主方程模型中首先需要确定的是车辆在集群中的吸引率w+和集群中车辆的消散率w-。 ①集群吸引率w+。 本文假设该模型中集群吸引率w+与集群数量N无关,等于总流量qsum。 ②集群消散率w-。 (11) 图5 消散率与集群大小的定性曲线Fig.5 Dissipation rate versus qualitative curve of cluster universities 从图5的特征曲线可以看到,确定性集群Ndet和临界随机集群Nc的大小分别为 0≤N≤Nd, (12) Nd≤N≤Ns, (13) 在给定qin、qon和qoff的情况下,特征曲线关于集群大小N的稳定性解满足如下方程: (14) 从图5可以看到,在满足公式(4)的流量范围内,水平线qsum与特征曲线至少相交于2个点:与N(det)的交点N=N1以及与Nc的交点N=N2,这是方程(14)的2个解。 定义ΔNc=N2-N1为临界车数差,其表示在给定qsum时,发生F→S相变所需要随机扰动引起的集群数量的增长值。由图5可以看到,qsum越大,ΔNc越小,说明所需要的临界增长值越小,则瓶颈处的F→S相变越容易发生;相反,qsum越小,ΔNc越大,所需要的临界增长值越大,瓶颈处的F→S相变越难发生。 对于主方程模型(8)—(10)有F→S相变平均延迟时间T的通用公式[28]: (15) 式中ps(N)是主方程的稳定性解, (16) 当Ni≫1(i=1,2)时,ps(N)函数在N=N1时有一个最大值,而式(15)中的函数ps(n)-1在N=N2时存在一个最大值。那么式(15)、(16)可以写成 (17) ps(N)=ps(0)exp[-Φ(N)],N>0, (18) 其中,势函数Φ(N)的表达式为 (19) 将式(18)代入式(17)中,可得 T=(w+)-1c1c2exp[Φ(N2)-Φ(N1)], (20) 式中: (21) ΔΦ(i)(N)=Φ(N)-Φ(Ni),i=1,2。 (22) 在极值点N=N1,N2附近,势函数的Φ(N)图像近似于抛物线,那么可以对c1、c2进行近似估计。定义变量y=N/N1,对式(19)、(21)近似积分求和可得 (23) (24) 将c1、c2代入式(20)中,可以得到F→S相变平均延迟时间TFS: (25) 因此,F→S相变概率GFS,即单位时间内交通拥堵发生的次数为 (26) 定义势阱函数ΔΦ=Φ(N2)-Φ(N1),观察式(25)可以看到ΔΦ对TFS的影响最大,呈指数级变化。根据式(19),势阱ΔΦ是ΔNc的单调递增函数。根据上文分析,ΔNc的大小与总流率qsum有关,因此势阱ΔΦ是qsum的递减函数,可知TFS的大小与qsum的变化密切相关。 首先对势阱函数ΔΦ近似,有 (27) 在Nd附近,对式(27)中的函数w-(N)用抛物线近似估计,可以得到 (28) 式中: N1,2=Nd∓ΔNc/2, (29) 根据式(28),可以解出: (30) (31) 计算c1、c2中的导数w-′(Ni)得 (32) 将式(31)、(32)代入(25)中,则可得到F→S相变平均延迟时间的近似公式: (33) 因此GFS为 (34) 根据上文对w-的定性分析,这里先给出w-的简单表达式, w-(N,qin,qon,qoff)=f(N,qon,qoff)+ηqoff+g, (35) 式中:f(N,qon,qoff)描述的是入口匝道和出口匝道所形成的组合瓶颈效应;g表示入口匝道车流和主干道车流交织对瓶颈附近的集群消散率的影响。现在讨论等式右侧中的每一项的具体表达式。 组合匝道的瓶颈效应与入口匝道流量qon和出口匝道流量qoff有关,同时为了满足三相交通流中w-的定性形状,f(N,qon,qoff)表达式如下: (36) 式中:a、b、N0都是qon和qoff的函数:a(qon,qoff)=1.32q0(qon,qoff)/N0(qon,qoff),b(qon,qoff)=23+10[1+(qon,qoff)/250]-1,N0(qon,qoff)=31.5-6.5[1+(qon,qoff)/300]-1,q0(qon,qoff)=2330+370[1+(qon,qoff)/300]-1。 交通波理论在分析交通流运行过程中,特别是在研究瓶颈处交通状态的转变以及交通流的拥堵和消散的传播特性方面有着十分广泛的应用[29]。假设qin和qon均符合均匀分布,并且qin大于qon。由于本文中所讨论的是位于主干道上的集群的消散率,因此只对主干道上所形成的交通波进行分析,而忽略匝道内部形成的交通波。 对于入口匝道,由于主干道车流量较大,因此入口匝道的车流将较难汇入到主干道,导致入口匝道车流将会选择强行汇入,使得主干道车流被迫让行而停下,在匝道和主干道合流区形成一个短距离的停驶区(称为P区)。P区的流量很小,密度接近于阻塞密度,类似于信号交叉口停车线附近区域。入口匝道的车流汇入过程将产生两个波: P区与qin形成一个交通波ω1, (37) 该波向后传播,类似于压缩波或者停车波。 qon和区域P形成一个波ω2, (38) ω2向后传播,类似于信号交叉口的起动波。式中kin、kon、kp分别是流量qin、qon、qp对应的密度。由于本文所描述的是自由流中的相变,因此流量和密度符合线性关系,此处采用格林希尔兹模型来描述这种关系[q=80k(1-k/150)]。将单位时间内集散波所掠过的车辆数称为波流量,则该过程得到2个波流量qω1和qω2,即 (39) (40) 于是得到了入口匝道造成的瓶颈效应对集群消散的影响, (41) 式中,ε=qon/(qon+qin)。 至此,得到了消散率w-的表达式(w-≥0), (42) ①消散率w-。 图6表示的是在给定主干道上游来流量qin和出口匝道流量qoff(qin=1 900 veh/h,qoff=100 veh/h),不同的入口匝道流量qon下的集群消散率变化曲线。对比这3条曲线可以发现,随着qon的增加,在相同的集群数量N的情况下,消散率在逐渐减小,这说明qon越大,其汇入对主干道车流造成的影响越大,集群中的车辆越难消散。同时可以看到,临界确定性集群Nd对应的临界流量qdet(图中虚线所对应的值)随着qon的增大而减小且十分明显,正如上文所描述的那样,qdet表示在发生F→S相变前总流量qsum所能达到的最大值,意味着在入口匝道流量较大时,qsum的增大将更容易导致F→S相变,入口匝道流量的增加将加快F→S相变的进程(qsum越容易接近qdet,相变发生所需要的临界随机扰动也就越小)。 图6 不同入口匝道流量时的消散率 Fig.6 Outflow rate for different on-ramp flows 图7表示的是在给定qin和qon(qin=1 900veh/h,qon=300 veh/h),不同的出口匝道流量qoff下的集群消散率变化曲线,对比这2条曲线可以发现,在相同的集群数量N的情况下,qoff=100 veh/h的消散率要小于qoff=300 veh/h消散率,因此qoff的增加促进了车辆集群的消散,同时可以看到qdet随着qoff的增加而显著上升,qoff的增加显然对维持交通流的稳定性起了一定的作用。事实上,由文献[10]可知,当qoff的比重(qoff占qsum的比重)低于15%~20%时,出口匝道流量的增加能更好的抑制交通拥堵,图7所表示的最大出口流量不超过总流量的18%,超过该值出口流量的增加将导致交通流的不稳定,但该研究是针对于同步流中的相变,本文研究的是自由流中的相变。 图7 不同出口匝道流量时的消散率 Fig.7 Outflow rate for different off-ramp flows 图8表示的是在qon和qoff(qon=300 veh/h,qoff=100 veh/h),不同的主干道来流量qin下的集群消散率变化曲线。尽管2条曲线的大小差别非常大,但是可以发现2条曲线几乎重合,说明qin的增加对车辆消散的影响不大:一方面qin的比重在一定范围内增大造成的影响远不如匝道流量增加所带来的扰动;另一方面则是qin增加并未让总流量qsum接近临界流量qdet,交通流仍处于自由流阶段。 图8 不同主干道上游来流率时的消散率 Fig.8 Outflow rate for differentupstream flow rates on major roads 对比图6、7、8可以发现,qon是对消散率w-减少影响最大的因素,同时qon的增加使得交通流更加不稳定,意味着F→S相变更为容易发生,事实也正是如此,qon的增加将会给主干道车流造成巨大的影响,因此将入口匝道流量控制在一定范围内十分必要。下面将重点研究qon的变化对其他参数造成的影响。 ②势阱ΔΦ和临界车数差ΔNc。 图9、10表示的是在给定qoff(qoff=100 veh/h),不同的入口匝道流量qon下的势阱ΔΦ和临界车数差ΔNc变化曲线,在qon给定的情况下,ΔΦ和ΔNc是总流量qsum的减函数。由ΔΦ和ΔNc的表达式可知,二者都和水平线qsum与w-曲线的交点N1、N2有关,随着qsum的增大,N1和N2的值越接近,ΔΦ和ΔNc也就越小,这也意味着F→S相变发生所需要的临界随机扰动也就越小。对比图9和图10中的3条线可知,在相同的qsum时,ΔΦ和ΔNc的值逐渐减小,因此它们同时也是入口匝道流量qon的减函数。 图9 不同入口匝道流量时的势阱Fig.9 Potential barrier for different on-ramp flows 图10 不同入口匝道流量时的临界车数差Fig.10 Critical vehicle number for different on-ramp flows ③F→S相变平均延迟时间TFS和相变概率GFS。 图11、12表示的与图10相同的匝道流量,F→S相变平均延迟时间TFS和相变概率GFS变化曲线。对于其中某一条曲线而言,当总流量qsum满足qth 图11 不同入口匝道流量时的相变平均延迟时间Fig.11 Mean time delay for phase transition at different on-ramp flows 值得注意的是,在所有的曲线中qsum的值始终小于相变发生的临界流量qdet,表明组合匝道瓶颈处的随机扰动的增长导致了随机交通拥堵的发生。从图12中可以看到,GFS曲线在临近qdet时上升趋势变缓,说明其存在一个小于1的临界值,即随机交通拥堵的边界趋近于确定性交通拥堵边界。同样地,在qsum极限趋近于阈值流量qth时,其存在一个大于0的阈值边界,与Kerner基于三相交通流微观仿真的结果一致[9]。 图12 不同入口匝道流量时的相变概率Fig.12 Phase transition probability for different on-ramp flows 本文基于三相交通流理论,借助了一类交通流中观模型——概率论主方程模型用以研究具有一个连续入-出口匝道瓶颈处的交通拥堵现象。通过引入速度适应效应和过加速效应,表明交通拥堵的发生就是自由流到同步流的一阶相变,并且具有概率性。本文创新性将主方程模型应用于匝道瓶颈处的集群变化描述,在假定集群吸引率等于总流量的前提下,结合组合匝道瓶颈效应和交通波理论重点分析了集群消散率并给出了具体的表达式,进一步推导出了交通拥堵的平均延迟时间和相变概率的表达式。 分别探讨了不同的入口匝道流入量、出口匝道流出量和瓶颈上游来流量对组合匝道瓶颈处车辆集群消散率和F→S相变发生的临界流量的影响,得出了相关结论:入口匝道流量的增加将加快F→S相变的进程,出口匝道流量在一定范围内对维持交通流的稳定性有促进作用,并且主干道流量不大时对车辆的消散影响较小。此外,重点分析了入口匝道流量和总流量的变化对F→S相变的平均延迟时间和相变概率的影响,结果表明在总流量小于临界流量时,总流量越大,相变概率越大,进一步说明合理控制入口匝道流量的范围对减少交通拥堵的发生十分必要。

1.3 Z形速度-流量函数和S形密度-流量函数

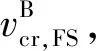


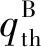

2 构建主方程模型
2.1 场景描述

2.2 主方程



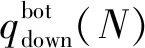
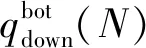
2.3 稳定性解

3 瓶颈处交通流相变概率


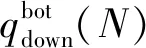
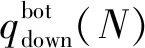
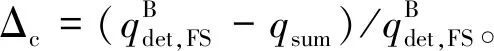
4 结果分析
4.1 消散率w-的定量表达
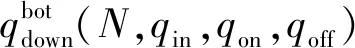
4.2 结果分析

5 结论

