基于腔光力系统的非经典态制备

廖长庚，王嘉佳，何宇虹，林秀敏

(1.浙江工商大学信息与电子工程学院(萨塞克斯人工智能学院)，浙江 杭州 310018；2.福建师范大学物理与能源学院，福建省量子调控与新能源材料重点实验室，福建 福州 350117；3.福建省太阳能转换与储能工程技术研究中心，福建 福州 350117；4.福建省先进高场超导材料协同创新中心，福建 福州 350117)

光力学最早可以追溯到1619年，开普勒在观测彗星时发现远离太阳的方向上会出现很长的慧尾，并认为这是辐射压力的结果[1].1871年，麦克斯韦首次从电磁学理论出发预言了光能够产生辐射压力[2]，并得到Lebedew的实验验证[3].但由于辐射压力非常微弱，必须对它进行仔细分析才能与光的热效应区分开来[4]，因此人们对上述实验仍存在一定的争议.之后，爱因斯坦进一步从理论上研究了作用在可移动腔镜上的辐射压力涨落统计以及摩擦效应[5].然而在很长的一段时间里，要想直接观测光的辐射压力依然困难.直到1972年，贝尔实验室的Ashkin在实验中通过将激光高度聚焦形成激光微束，实现对微粒进行移动控制或逆着重力进行提升，从而毫无争议地证明了激光的辐射压力[6]，并因此成为利用激光光压囚禁粒子的先驱.与此同时，随着引力波探测的兴起，腔光力系统的雏形逐渐形成，并于20世纪90年代在高精密传感领域获得应用[7-8].在腔光力系统中，微弱的电磁辐射压力可以通过谐振腔进行放大，进而驱动可动腔镜成为机械谐振子，动量可以在电磁辐射和机械谐振子之间进行交换.

到了21世纪初期，随着微纳加工技术的进一步发展，科学家们开始致力于将机械振子制备到接近它们的量子基态上[9]，在这种情况下，能量的量子化和不确定性关系对系统的动力学有着显著的影响.同时，建立在标准微芯片技术基础上的微纳加工技术也为腔光力系统提供了独特的可集成性、可操控性和可扩展性的潜力.该技术通过在光学腔[10]或超导微波电路中[11-13]嵌入纳米或微尺度机械谐振子，使其与电磁辐射的较强耦合成为可能，并进而实现压缩、纠缠等量子态的制备和操控，这直接促使腔光力学系统成为未来量子技术有效物理载体的候选者之一[14].

一方面，腔光力系统中机械振子的空间和质量尺度范围很广，将机械振子制备到非经典态，例如薛定谔猫态上，有助于揭示从经典物理到量子物理的转变机制；另一方面，腔光力系统中的机械振子具有较长的衰减时间，同时该系统易于和其他物理系统耦合构成杂化量子体系，因此，它在量子存储、量子精密测量、量子网络接口等量子信息处理领域中具有广阔的应用前景.本文主要聚焦于机械谐振子的非经典态以及腔光力系统中的压缩和纠缠等，首先从最简单的腔光力系统出发，简要地介绍其光力相互作用的基本原理，以便更好地理解如何在该系统中实现光力冷却以及纠缠等；然后综述腔光力学在非经典态制备，尤其是利用周期性外场调制和库工程技术实现压缩、纠缠以及非对称量子导引等方面的研究进展，最后对未来的潜在应用进行展望.

1 腔光力系统中光力相互作用的基本原理及基本应用

光力相互作用涉及光与振动物体动量的交换，单个光子撞击到振动物体表面所产生的冲量非常微弱，为了提高光子与机械振子之间的有效相互作用强度，需要将光限制在光学腔或微波腔中，通过增加相互作用次数来提高平均的辐射压力.图1是典型的腔光力系统示意图，在光域(图1(a))，它是由一个激光驱动的光学腔组成，其中腔的一端固定，另一端可左右来回微小地振动，形成机械谐振子；在微波域(图1(b))，它是由一个微波驱动的LC电路组成，其中鼓形电容的极板可构成机械振子.以下将从最简单的腔光力模型出发，给出腔中的电磁辐射与机械振子相互作用的量子理论描述，并说明其相应的应用.

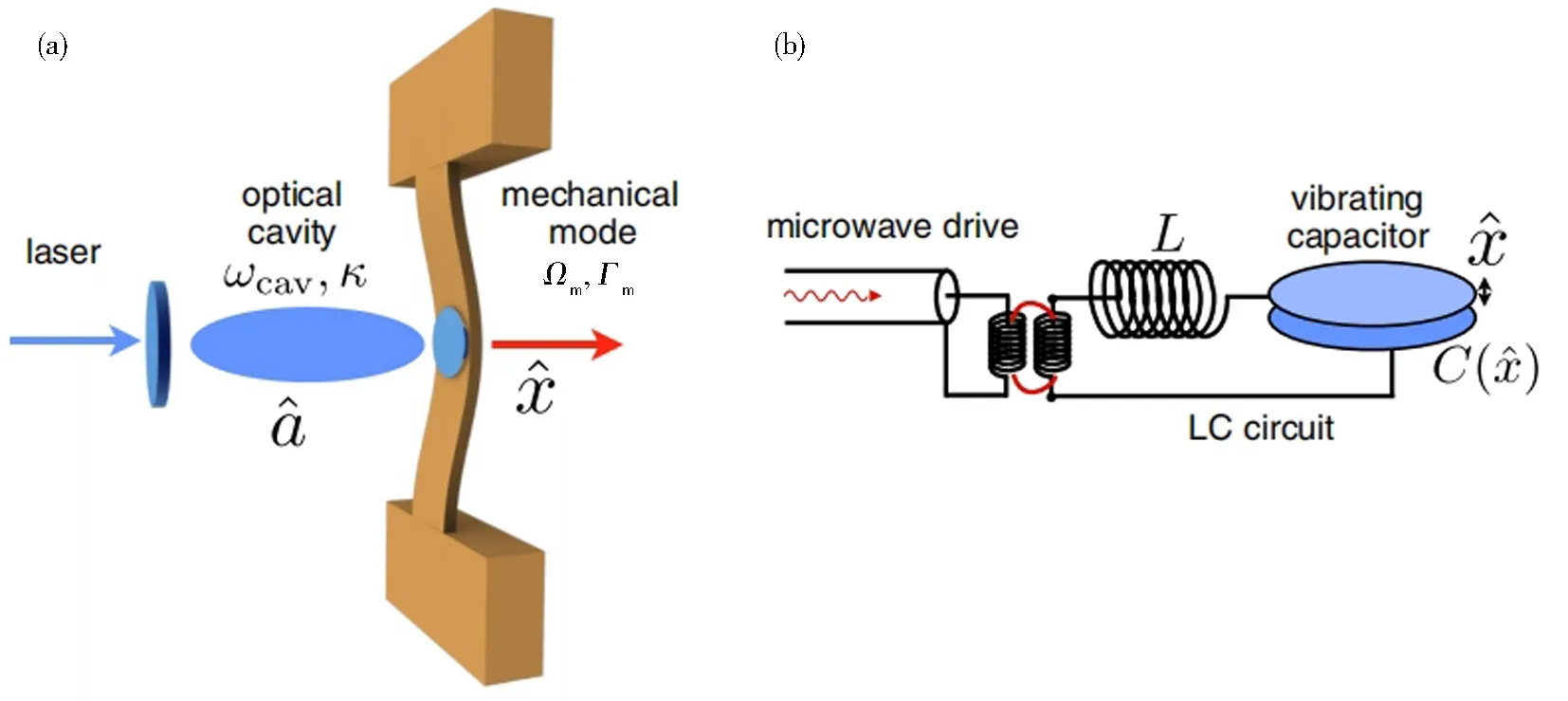
图1 典型的腔光力系统示意图[14]Fig.1 Schematic of a generic optomechanical system[14]

考虑单个光学或微波腔模和单个机械振动模式相互作用情形，它们在量子理论中可以分别看作频率为ωc和Ω的两个量子谐振子a和b，哈密顿量为

H0=ћωca†a+ћΩb†b.

(1)

受机械振子振幅的调制，腔模的频率是机械振子位移的函数，可近似展开为

(2)

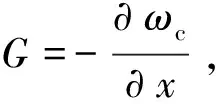
H0≈ћωca†a+ћΩb†b-ћGxa†a.

(3)

将机械振子的位移写成谐振子的产生和湮灭算的形式x=xZPF(b+b†)，式(3)改写为

H0=ћωca†a+ћΩb†b-ћg0a†a(b+b†)，

(4)

其中g0=GxZPF可用于表征单个光子与声子的相互作用强度，其通常较弱.为了提高有效光力耦合强度，需要施加外部的激光进行驱动，这样，总的哈密顿量还要加上激光驱动项

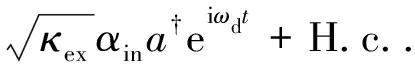
(5)

这里，κex为输入耦合相关的损耗率，αin为激光的振幅.以激光频率ωd为参考进行旋转变换，在旋转坐标下，对腔场作线性化处理，即把湮灭算符写成平均值加涨落项a=〈a〉+c，可得到线性化的哈密顿量

Hlin=-ћΔc†c+ћΩb†b-ћg(c†+c)(b+b†)，

(6)

其中激光与腔模失谐量Δ=ωd-ωc，有效耦合g=g0〈a〉.这里〈a〉的相位在动力学演化中不起作用，可以忽略不计，但其振幅可以显著提高有效耦合强度.在相互作用绘景中，式(6)可以写成

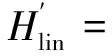
(7)

在边带可分情况下(腔场总的损耗率κ≪Ω)，通过选择不同频率的激光进行驱动，可以获得不同的相互作用机制.例如红失谐驱动下(Δ≈-Ω)，通过旋波近似忽略快速振荡项(±2Ω)，可获得分束器型相互作用哈密顿量

HBS=ћg(cb†+c†b)，

(8)

利用该哈密顿量可实现光子和声子数的交换，通过边带冷却实现对机械振子的冷却等[15-16].在蓝失谐的激光驱动下(Δ≈Ω)，通过旋波近似可获得参量下转换型(双模压缩型)相互作用哈密顿量

HPDC=ћg(c†b†+cb)，

(9)

利用该哈密顿量可实现光子和声子的双模压缩纠缠.在不考虑耗散或耗散很小的情况下，若只关注机械振子，其存储的能量呈指数增长，出现“抗阻尼”、引发动力学不稳定并导致自激振荡现象[17-20].

将机械振子制备到基态(能量最低态或真空态)，这是完成腔光力系统复杂量子实验的常规起点.对于G赫兹的高频机械振子，利用稀释致冷机制可以直接将其冷却至基态[21].而边带冷却技术则可以将电力[22]和光力[9]系统中的机械振子冷却至基态.这项技术使得研究频率低至M赫兹的量子基态谐振器也成为可能[23].

2 腔光力系统中非经典态的制备

在腔光力系统中制备非经典态大致可以分为两类，一类是利用非线性的全哈密顿量实现非高斯态(如薛定谔猫态)的制备，这需要足够大的单光子耦合强度.对于两对空间分离的离子构成的机械振子，较容易实现单光子强耦合，它们之间的纠缠已于2009年被Jost等[24]实验证明.但在其他的许多腔光力物理体系中，目前还比较难以实现单光子强耦合，很多工作仅局限于理论探讨.1997年，Bose 等[25]以及Mancini等[26]分别从理论层面讨论了如何产生“Schrödinger cat”类型的状态：即一种“微观”自由度(光学腔模式)与“宏观”(或介观)自由度(振动镜)之间的纠缠.利用电磁诱导透明以及参量下转换等方法，Li等[27]提出了实现非高斯添加声子相干态(non-Gaussian phonon-added coherent states)的理论方案，并且理论论证了如何在没有相互作用情况下将未知的光输入状态转移到一对机械振子的状态上，实现光力量子隐形传态[28].北京大学Liu团队[29]理论分析论证了非线性光力学相互作用能够导致参量下转换，进而产生由光子和声子形成的极化子对，同时基于单模光纤耦合光力系统研究了单光子传输以及力学NOON 态的产生[30].Xu等[31-32]利用边带激发或结合阻塞效应提出了制备机械振子任意非经典态的理论方案.华中师范大学的Tan等[33]利用有效简并三波混频相互作用结合腔耗散、量子干涉效应[34]、光子探测[35]等方法提出了制备宏观机械振子量子叠加态的理论方案.湖南师范大学Liao等[36-38]在宏观薛定谔猫态、机械振子间的宏观纠缠等方面也做出了许多出色的工作.2018年，华中科技大学的Lü等[39]在Rabi模型中引入光力耦合，预测了混合量子模型中单光子诱导纠缠和量子叠加态的发生.本课题组基于二次方耦合腔光力系统在单光子非线性[40]、声子阻塞[41-42]以及机械振子的薛定谔猫态[43]等方面也做了一些工作，同时将该研究进一步拓展到腔光磁系统中的非互易光子阻塞[44].2019年，通过在腔光力系统中引入调制光子跳跃相互作用，大连理工大学的周玲团队[45-46]分别提出了产生宏观纠缠薛定谔猫态和压缩相干猫态的理论方案.在实验方面，该领域近年来也取得了迅猛的发展.2018年，美国耶鲁大学的研究人员实验演示了在宏观尺度谐振器中受控多声子Fock态的产生[47].最近，由1017个原子组成的宏观机械振子在实验中被制备到两个相反相位振荡的叠加态中(相关实验结果如图2所示)[48]，这是迄今为止最大的薛定谔猫态，重达16 μg.

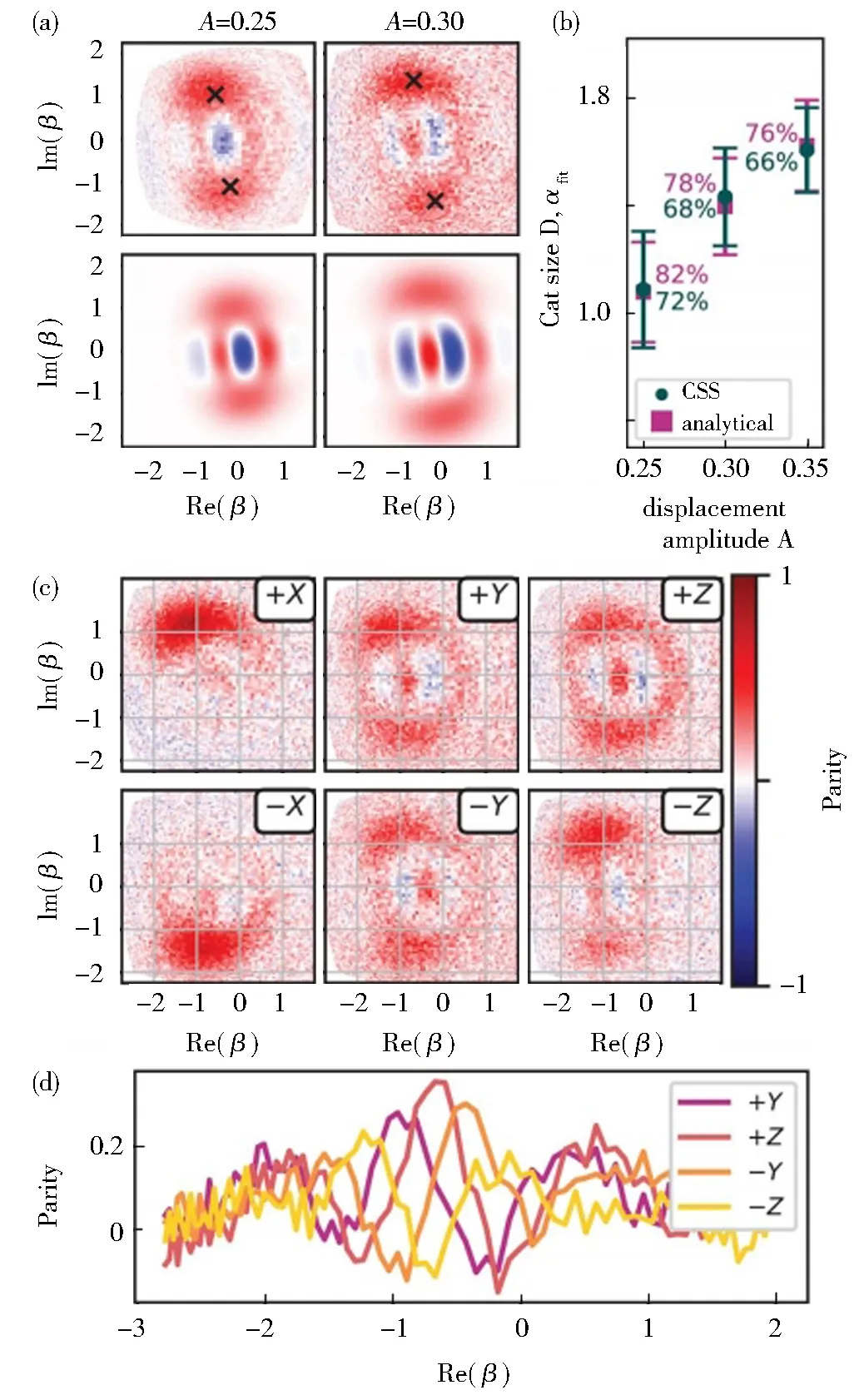
(a)不同位移脉冲幅值制备的猫态；(b)猫态大小随位移振幅变化的函数；(c)由各自标签指示的初始量子比特状态产生的猫态；(d)对应于图(c)中4个初始量子比特状态的干涉条纹横切面图2 猫态振幅和相位控制[48]Fig.2 Cat state amplitude and phase control[48]

另一类制备高斯非经典态(例如压缩态以及连续变量纠缠态)是利用线性化处理后的哈密顿量来实现.只要系统的初始状态为高斯态(例如热态)，系统在演化过程中将始终保持高斯状态，因此它对初态不敏感.这类状态可以由机械振子和光学广义正交分量对应的协方差矩阵完全表征，一个典型的度量高斯纠缠的方法是负对数(logarithmic negativity)[49]，它既适用于纯态也适用于混合态.

类似于压缩光，产生机械振子的压缩在超高精密测量[50]以及引力波探测[51-53]等方面也有着潜在的应用.早在2007年，纳米力学物体的压缩实验已经在非线性Duffing谐振器中实现[54].结合Duffing 非线性以及腔模的红失谐单色驱动，可以获得非常强的稳态力学压缩[55].实现力学压缩的方法还有很多，通过将一个线性的纳米力学振子耦合到另一个辅助的非线性系统[56-59]、态转换[60-61]或直接通过调制以及参量驱动的方法[62-66]都可以实现力学振子的压缩.在文献[59，67]中，Zoller组提出了利用库工程产生压缩的方案.2020年，Xiong等[68]提出了一种利用李雅普诺夫控制在腔光力系统中产生强压缩的方案.最近，Li等[69]提出了一种失谐开关方法，可以快速产生强而稳定的机械压缩.

在高斯纠缠态制备方面，Paternostro等[70]以及Vitali等[71]于2007年详细分析了连续变量的机械振子和腔场间的纠缠.值得强调的是：利用周期性的振幅调制激光驱动系统，可以提高力学振子的压缩[72-77]以及光力系统中的纠缠[74，77-85].这种周期性调制的方法被广泛地应用到各种量子效应的提升上，包括超越边带可分条件的冷却[86]、单光子强耦合[87]、双重力学压缩[88]等，同时可以展示出丰富的经典和量子动力学行为[89].此外，双重周期性调制还能诱发干涉效应[90-92]、展示纠缠拍现象[93].在杂化腔光力系统中，利用原子相干性也可以诱发纳米机械振子间以及双模场间的纠缠[94].2012年，文献[95]研究了卡西米尔力对光机械系统中悬浮纳米球和腔模间纠缠态的影响.2013年，Tian[96]提出了在强耦合状态下通过光力量子接口产生鲁棒光子纠缠的方案.该方案探索了Bogoliubov暗模的激发和界面亮模式之间的破坏性量子干涉(类似于电磁诱导透明)，以消除机械噪声的leading-order效应，从而实现对机械噪声具有鲁棒性的连续变量和离散状态纠缠.最近，笔者将这一方法拓展到腔光磁系统中，用于实现两个正交偏振的光学模式间的鲁棒纠缠[97]，其在依赖偏振的量子信息任务中有潜在的应用.2020年，基于腔光力系统，微波光子与光波光子间可切换的两体和三体纠缠[98]也在理论中被提出来，这为不同频率下运行的混杂量子系统中的可控纠缠提供了思路.同年，华侨大学的Lin等[99]理论论证了放置在高温环境中的两个机械振子间的纠缠，该方案主要通过蓝失谐的激光驱动子系统，同时结合测量腔中泄漏出来的光子所诱发的纠缠交换过程来实现.受外界环境的影响，纠缠通常比较脆弱，文献[100]研究了非马尔可夫环境下腔光力系统的动力学问题.在弱单光子光力耦合情况下，该工作提供了一种充分考虑非马尔可夫记忆效应的分析方法，提供了在非马尔可夫环境中产生和保护纠缠的潜在用途.

从实验的角度来看，一种有望产生强纠缠或压缩的非常有吸引力的方法是通过向腔光力系统泵浦适当的蓝失谐和红失谐激光来诱导有效的工程库[79，101-110].值得强调的是这种方法已经在实验中得到证实[111].在双色驱动的基础上，文献[112]通过增加一个相干反馈回路，有效地降低了腔的衰减率，显著增强了纠缠度，从而大大扩展方案的有效性.结合光力相互作用和振子间的库仑相互作用，也可以诱导有效的工程库，其效果与双色驱动类似[113].受文献[104]启发，本课题组[114]提出了通过周期性调制和库工程技术来产生高纯度强光-力或光-微波纠缠的理论方案，该方案可以允许两个Bogoliubov模式的和模以及差模同时通过中介模式的耗散动力学过程得到冷却.此外，利用类似的方法，同时展示并显著提高了两个间接耦合的机械振子之间的量子同步和纠缠水平，并在腔光力系统首次预言了类量子同步阻塞效应[115].最近，利用级联的冷却动力学过程，一种在四模混合腔光力系统中产生两个微波场之间高纯度稳态纠缠的有效方法也被提出来[116].截至目前，相关的实验也取得突破性的进展.2013年，微波光子与机械振子间的纠缠已经在实验中证实[117]，其采用脉冲方案来实现[118].2018年，Nature上几乎同时报道了实验实现两个机械振子间纠缠的两个工作[111，119].其中文献[119]采用一种由纳米结构硅束制成的基于芯片的光学机械谐振器形式的纯微机械固态平台，在相隔20 cm的两个芯片上创建并演示了两个微机械振荡器之间的纠缠.而文献[111]则将两个巨大的微机械振子(每个机械振子由大约个原子组成)与一个微波频段的电磁腔耦合，用于产生和稳定它们的质心运动的纠缠.2021年，Kotler等[120]利用脉冲电力学，确定性地将两个质量为70 pg的铝膜构成的机械振子纠缠在一起(如图3所示)，通过对两个铝膜的正交位移和动量的近量子限制测量，其进行了量子态层析成像，从而直接观察到纠缠.

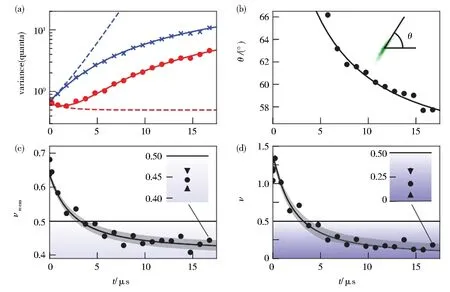
(a)单个鼓膜的测量方差；(b)关联角度决定了两体系统的压缩和反压缩联合正交；(c)用被测量度量的纠缠(考虑损耗以后)，低于的点意味着两个鼓膜是纠缠的；(d)用预估量度量的纠缠(未受损耗影响前的预估值)图3 两个鼓膜的纠缠与脉冲持续时间的关系[120]Fig.3 Entanglement of two drums versus pulse duration[120]

量子导引是另一类介于纠缠和非定域性之间的非经典关联，具有非对称的特征.除了具有基本的物理意义外，量子导引还具有许多重要的实际应用，例如量子子信道识别问题[121]，以及使用最低限度纠缠但可导引资源的高保真隐形传态[122]等.在腔光力系统中，有大量的工作探索如何实现宏观大质量物体间的量子导引[123-133]，其中包括力学振子与光场[123，125，132]、机械振子间[127，130-131，133]以及原子与机械振子间的混杂量子导引[124，128]等.此外，在机械振子介导的两个电磁场之间的单向量子导引[126]或腔场与机械振子间的单向量子导引[129]都有所涉及.本课题组[134]提出了一种在两个机械振子之间实现稳态单向量子导引的理论方案.在该方案中，采用的是多色驱动与库工程技术结合的方法，该方法同样适用于腔磁力系统[135].另一方面，也有一些有趣的工作从另外的视角进行阐述.例如文献 [136] 研究了级联双腔光力系统与普通单向光纤耦合的受驱动级联量子网络中的耗散动力学和纠缠态形成.文献[137]发现单向量子导引是两对纠缠模式实现高斯纠缠交换的充要条件，而以往的研究表明子系统在混合状态下存在纠缠只是实现纠缠交换的必要条件.

在前文所述工作中，不少方案是通过周期性调制或多色激光驱动结合库工程实现的.周期性地调制驱动激光的振幅或调制相互作用强度都能够使系统长时演化的稳态获得相同的调制周期，其作用是等效的.对于周期性地调制驱动激光的振幅，文献[72，74，78-79]的研究都表明：在典型的参数空间中，对于经典平均值，只考虑其对单光子耦合系数的幂级数和傅里叶级数双边展开中的第一项(对应第一边带)，就可以得到经典周期轨道的良好解析近似.从广义上来说，周期性地调制驱动激光的振幅或调制相互作用强度在压缩、纠缠、导引等量子效应的提升上与适当的多色激光驱动具有异曲同工的作用，其本质是相同的.通过选择适当强度和频率的多色激光驱动系统，并结合库工程技术可以达到良好的效果.

3 总结与展望

微纳加工、冷却以及量子调控技术的快速发展使得腔光力系统在基础物理研究和量子信息处理领域的作用越来越明显，其不但在微小位移、弱力等量子精密测量方面取得重要成果，在研究经典物理到量子物理的过渡等方面也展现出了重大的价值.随着越来越大尺度机械振子基态冷却的实现，各种不同类型的杂化腔光力系统可以进入量子区域，宏观、杂化的非经典态制备是各项研究和应用的起点，也是未来一段时间的研究焦点.

本文简要回顾了腔光力系统的发展历史，对腔光力系统中的光力相互作用基本原理和基本应用进行了介绍，主要综述了基于腔光力系统的非经典态制备，尤其是利用周期性外场调制和库工程实现连续变量的高斯纠缠以及非对称量子导引等方面的研究进展，最后对未来的潜在应用进行展望，可为相关研究人员提供参考.