密闭舱内氧传感器自动标定方法研究

潘点飞，刘力涛，唐 斌，葛江亚，王 魁，郑为阁

（中国航天员科研训练中心，北京 100094）

0 引言

氧是维持人与动植物生存必不可少的元素，氧浓度传感器和氧化锆传感器常用于测量气体中氧浓度或氧分压。氧浓度传感器和氧化锆传感器（文中统称为氧传感器），均采用电化学反应原理，将氧气成分转化为电信号，具有测量精度高、响应快、稳定性好等特点［1］，是检测密闭舱内氧气浓度的重要方法，被广泛应用于载人航天、潜艇、工业控制、医疗科研等领域。氧传感器均属于消耗性传感器，如氧化锆传感器，其使用寿命取决于电极的消耗，氧化锆传感器的性能由其核心材料陶瓷结构决定［2-8］。随着电极消耗、电解液蒸发和陶瓷结构稳定性降低，其测量精度、稳定性逐渐丧失，需采用定期标定的方法，保证其测量确定性［9-12］。常规环境下，可采用已知浓度的标气瓶进行校准，而在载人航天器、潜艇等特殊密闭环境下，常规标定方法不易实施，且成本高、风险大。

密闭舱内一般同时采用多组、多只氧浓度传感器和氧化锆传感器测量氧气成分，由于传感器分布位置不同、工作模式不同，其测量值的变化特性也不同［13］。当部分传感器性能下降时，其测量结果出现精度误差及漂移特性，导致各传感器之间的测量值表现出不一致性。为适用密闭舱内长期测量的需求，研究氧传感器自主高效的标定方法，是保证氧气成分测量精度、稳定性和可靠性的有效手段。

根据传感器测量数据，对数据分析处理，提取数据变化特征，采用基于数据融合技术的自动标定方案。监测到氧气成分测量数据超出额定阈值时，实施系统自动标定，既提高传感器定期标定的效率，又保证密闭内氧气成分测量准确性与稳定性，进而延长氧传感器的使用寿命。

1 多传感器数据融合技术

多传感器数据融合，利用多种类型、多只数量传感器的信息与数据，在一定的准则下进行综合分析处理，以获得更加有效的数据信息。与单一传感器数据相比，多传感器数据融合技术提高了测量信息的可靠性与健壮性，增强数据的可信度，提高信息的利用率。传感器数据融合与概率统计、神经网络、模式识别、人工智能等技术后相结合，在信息化、智能化、全局化等方面提供广阔的应用空间［14］。

多传感器数据融合的形式常分为3 类：数据级融合、特征级融合和决策级融合。数据融合的方法有加权法、滤波法、神经网络法等［15］。不论采用何种方法，传感器测量偏差值（甚至失效数据）均会影响到最终的测量结果，导致对环境信息错误判断。分析并处理传感器采集的数据，识别异常数据，筛选出最优基准值，对增强密闭舱氧传感器标定的可靠性及鲁棒性具有重要意义。

检测测量数据异常值的方法较多，常用的方法有罗曼诺夫斯基准则、狄克松准则、格拉布斯准则以及拉依达准则等［16］。格拉布斯准则在数据量不大的情况下，可靠性能较好，本文在该准则的基础上，提出基于多传感器数据融合技术的自主氧传感器标定方法。

利用格拉布斯准则对传感器测量数据进行残差值分析判断，如测量值超过格拉布斯临界值，则认为该测量值为不可靠数据，不能参与传感器标定的基准值计算。将传感器测量数据按从小到大排序为yi，其中y1＜y2，...，yn，n为样本数，yˉ为平均值，σ为标准差，g0(n，a)为统计临界数值，可得g1、gn分别为

如g1≥gn且g1＞g0，则认为g1为异常值；如g1＜gn且gn＞g0，则认为gn为异常值；如g1＜g0且gn＜g0，则样本数据中不存在异常值。统计临界数值g0(n，a)见表1［17］，其中n为样本数，a为显著水平，0.050 和0.010 为错输概率，对应置信概率分别为95%和99%。

表1 临界值表Tab.1 Critical value table

多只传感器同时测量舱内氧分压，测量数据之间的相互关联性反映传感器变化的一致性，确定一致性及稳定性较好的传感器测量值作为基准值，是氧分压传感器自主标定的基础。

假设某一时刻，氧传感器i、j测量结果分别为Ti和Tj，引入dij表示测量值Ti与Tj之间的融合度，dij越大表示传感器i与j的测量值相差越大，反之则两者偏差越小。

式中：Qi为Ti的方差。

其表达式为

如舱内同时存在m个传感器测量当前氧分压，各传感器之间的融合度dij（i，j=1，2，…，m）构成融合度矩阵Dm。其表达式为

依据相容矩阵及相容性阈值，将相容矩阵进行归一化处理，得到标准化相容矩阵Rm。其表达式为

rij表达式为

式中：pij为传感器相容性阈值。

如果rij=0，表明传感器i与j的相容性差，相互不关联。如果rij=1，表明传感器i与j的相容性强，两者相互关联［18］。如某一传感器测量值仅被少数传感器测量值关联，则认为其测量结果不可靠，不适合作为标定基准值。反之，如某一传感器的测量值与多数传感器测量值相关性强，则其为强关联数据。据此可得到强关联数据融合集，有利于确定可靠的标定基准值。

2 传感器测量数据变化特性分析

以氧化锆传感器为例，在氧化锆传感器寿命末期，传感器的陶瓷结构稳定性及气体扩散孔稳定性逐渐降低，氧传感器敏感探头中的电解液缓慢挥发，电化学反应活性变弱［19］，导致其测量精度和稳定性变差。处于寿命末期氧化锆传感器a、b、c 的测量值漂移特性曲线如图1 所示。

图1 氧化锆传感器测量曲线Fig.1 Measured curves of the zirconia oxygen sensors

由图1 可知，密闭舱内氧浓度维持在约22 kPa的情况下，传感器a 呈缓慢上升趋势，传感器b 呈下漂降趋势，传感器c 呈先上漂后快速下漂的趋势。在实际应用中，为提高测量可靠性，在同一位置往往布置多只传感器，每组传感器通过特定取平均算法，获得最终测量的物理值。当同组氧化锆传感器相互测量偏差超过额定阈值，将导致该组传感器无法得到有效的测量结果，甚至引起传感器多只超差报警提示。

上述传感器a、b、c 相对基准值测量偏差如图2所示。如3 只传感器属于同组配置，将出现异常结果。因此，通常采用传感器系数重新标定的方法，消除漂移影响，延长传感器使用寿命。

图2 氧化锆传感器测漂移量曲线Fig.2 Drift curves of the zirconia oxygen sensors

氧浓度传感器、氧化锆传感器的物理值计算公式为

式中：x为传感器测量电压值，V；P为环境总压，kPa；A、B为公式系数；y为氧气成分物理值；e为常数，取2.718 3。

修正计算公式中的系数A、B均可达到消除漂移的目的。其中，氧浓度传感器为线性公式，可直接通过修正系数获得标定后的新系数。本文主要分析氧化锆传感器的自标定方法，其基准值确定策略及系数修正流程同样适用于氧浓度传感器，不再赘述。上述方法需先确定校准基准值，再根据经验公式反算出校准后的系数，最后由控制器软件实施系数更新。

地面环境中，可通过校准气瓶确定待标定的基准值，但不易确定在轨航天器的校准基准值。系统软件更新维护流程繁多复杂、风险点多、不易控制。从待标定的传感器系数确定，到系数更新真正实施需要一定周期，存在滞后性，导致传感器更新后的系数时效性较差。

3 多k 值标定方法实现与验证

3.1 传感器标定基准值确定

以地面长寿命验证试验中的氧传感器a～h 为例，采用前文所述多传感器数据融合技术，筛选稳定性和一致性较好的传感器测量值作为标定基准值。

选择2 个不同时间氧传感器测量数据，分别设为Ti和Tj，各传感器测量值见表2。

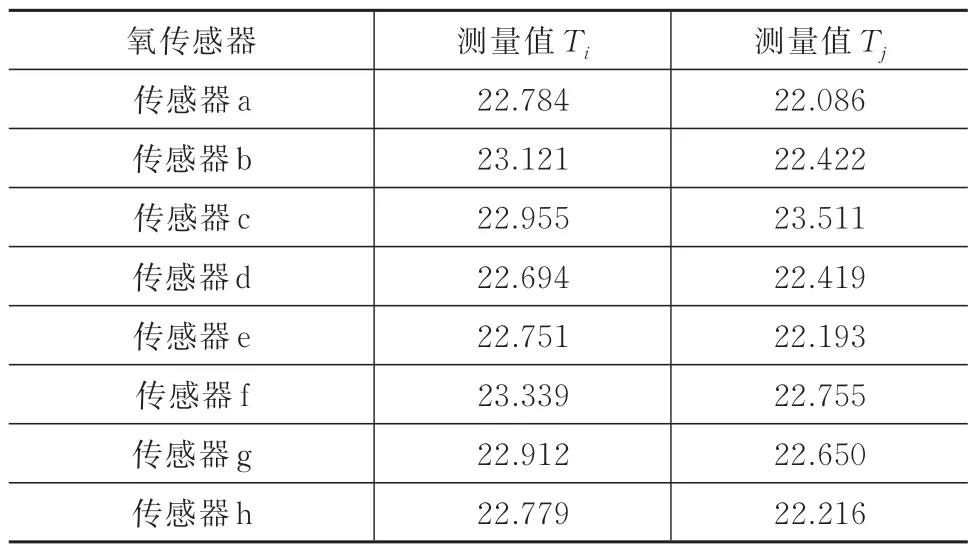
表2 氧传感器测量结果Tab.2 Measured results of the zirconia oxygen sensors

由表2 可知，Ti=［22.784 00，23.121 27，22.955 00，22.694 00，22.751 00，23.339 00，22.912 00，22.779 00］，将传感器测量结果由小到大排序为［22.694 00，22.751 00，22.779 00，22.784 00，22.912 00，22.955 00，23.121 27，23.339 00］，其均值为22.531 4，标准差0.427 3，测量值残差矩阵为g=［1.042 8，0.791 9，0.738 1，0.263 1，0.257 0，0.277 5，0.523 2，2.292 3］，n=8，依据格拉布斯表取g0=2.032，g1＜gn且gn＞g0，认为gn为异常值，其对应的测量值不可靠，将其剔除后传感器测量均值为22.856 6。

同理，计算氧传感器数据Tj均值为22.391 5，剔除异常值后，不同时刻传感器测量平均差值为0.465 1，并将其设为相容性阈值，其中T1为：Tj=［22.085 8，22.421 6，23.511 0，22.419 0，22.193 0，22.755 0，22.650 0，22.216 0］。因此，不同时刻各传感器测量数据之间融合度矩阵Dm为

根据相容性阈值0.465 1，对相容性矩阵进行归一化处理，得到标准化相容矩阵Rm为

据此可得各传感器测量结果的关联性，序号为1、5、8 的3 只传感器测量结果与其他传感器测量值强关联，可将其作为传感器标定的基准值。

3.2 单点k 值标定方法

密闭舱内氧化锆传感器系数标定主要采用单点k 值标定方法，即选择标定时刻t1氧化锆传感器测量结果与舱内氧分压基准值的修正系数k，通过五点曲线拟合方法，得出当前待修正传感器系数。具体步骤如下。

1）根据专家知识库，选择稳定性及一致性较好的氧浓度传感器测量值作为标定基准值Y0。

2）通过氧化锆传感器输出Y1与基准值之间的偏差，得到修正系数k=Y0/Y1。

3）假设总压P为100，氧浓度T为10～30 kPa的氧化锆传感器与氧传感器一致性好，此时对应未修正的氧分压则为氧浓度T/k，根据氧化锆计算公式，反算出氧化锆电压值应为

式中：A和B为当前未修正的系数。

1）选取10～30 范围5 个点，根据上述反算公式得到电压和输出之间的5 个点关系。

2）根据这5 个点，拟合出新的修正后公式系数A′和B′。设A′和B′为正，氧分压公式表示为

如选取t1时刻的修正k值（单点k值），即可实现对该时刻传感器测量电压x1的修正。其中，10～30 kPa 范围内的修正一致只是一种理想假设。但实际上，在氧化锆传感器寿命末期，即使舱内氧分压未发生变化，其测量电压值会不断漂移，一旦氧化锆测量电压继续漂移，上述修正效果则明显降低。

分析试验数据，密闭舱内氧分压大部分时间维持在22～23 kPa，氧化锆测量值不断漂移（上漂或下漂），其实质是传感器电压值漂移。常规修正方法仅实现了当前电压值下测量的一致性，当电压继续漂移，修正系数k无法保证电压为x2时的一致性。因此，单一k值修正方法的适应范围较窄，导致传感器系数修正的频次不断增加。

3.3 多点k 值标定方法

将原单点k 值修正法改进为多点k 值修正法，即选取t1时刻对应的电压值x1及修正值k1，再选取氧分压修正范围漂移1 kPa，对应t2时刻的电压值x2及修正值k2，根据氧化锆公式可得：

如氧分压漂移修正范围选择1 kPa，考虑氧分压公式中总压变化的影响，取舱内总压经验值上限，即P2为100 kPa，则上式中，Y2=Y1±1，P2=100 kPa，根据上述多项式可求得修正后的传感器系数A′和B′。

该方法可保证氧化锆传感器测量电压值在x1～x2范围内漂移，与基准值修正一致。

3.4 方法验证

以地面长寿命验证试验中的传感器为例，对处于寿命末期的3 只氧化锆传感器Ⅰ、Ⅱ和Ⅲ进行系数标定，修正前后，氧分压传感器系数见表3。

表3 氧化锆传感器标定系数（单点k 值）Tab.3 Calibration coefficients of the zirconia oxygen sensors（single-point k-factor）

上述3 只氧化锆传感器于ti进行单点k 值系数修正，修正后其测量结果与基准值一致。随传感器工作时间增加，在舱内氧分压基本稳定的情况下，其测量结果仍不断漂移，2 个月内各传感器测量漂移量如图3～5 所示。

图3 氧化锆Ⅰ、Ⅱ、Ⅲ单点标定曲线Fig.3 Results of the zirconia oxygen sensors Ⅰ，Ⅱ，andⅢ obtained by the single-point calibration method

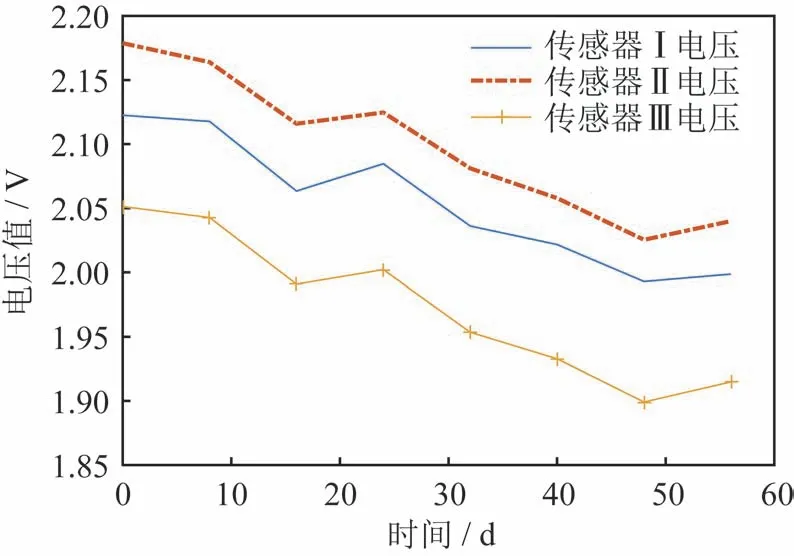
图4 氧化锆Ⅰ、Ⅱ、Ⅲ电压值漂移量曲线Fig.4 Voltage drift curves of the zirconia oxygen sensorsⅠ，Ⅱ，and Ⅲ

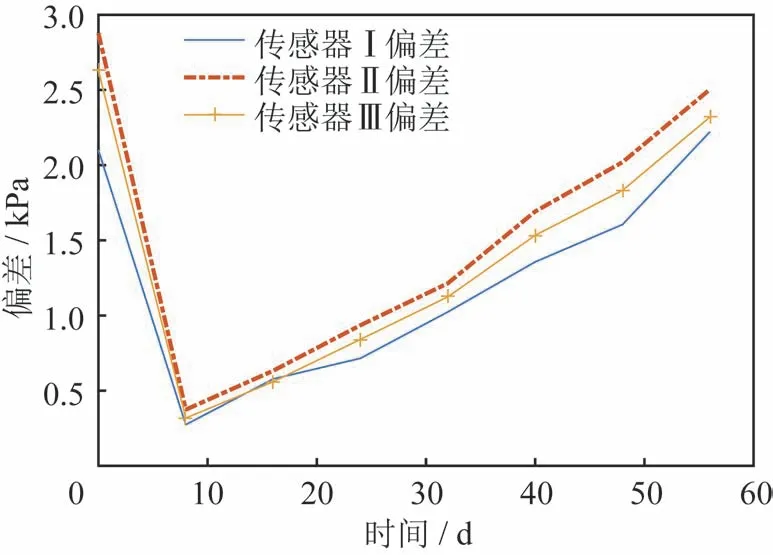
图5 氧化锆Ⅰ、Ⅱ、Ⅲ物理值漂移量曲线Fig.5 Physical quantity drift curves of the zirconia oxygen sensors Ⅰ，Ⅱ，and Ⅲ

采用单点k 值标定后，在一定程度上延长了氧化锆传感器使用寿命，但其输出物理量（氧分压）与基准值的差异仍在持续增大，直至超出额定阈值。综上所述，该方法适应范围较窄、延寿效果有限。

采用多点k 值点修正方法，氧化锆Ⅰ、Ⅱ和Ⅲ的修点同样选择t1时刻，修正范围为1 kPa，则由式（14）与式（15）可得到新的修正系数，见表4。

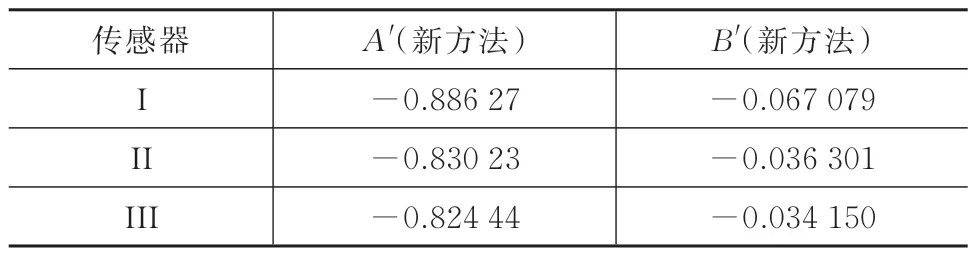
表4 氧化锆传感器标定系数（多点k 值）Tab.4 Calibration coefficients of the zirconia oxygen sensors（multi-point k-factor）

采用前文多传感器数据融合方法，确定标定基准值为1、5 和8 的3 只氧传感器测量平均值，采用多点k 值修正方法得到修正结果，如图6 所示。

图6 2 种标定方法比较曲线Fig.6 Comparison curves of two calibration methods

单点k 值标定方法，在k 值选定标定时刻的标定效果较好，但随着传感器测量电压值的继续漂移，2个月后，测量电压值漂移量达0.1 V，相应物理量漂移超过2.0 kPa。而多点k 值标定方法，在相同传感器电压漂移量下，物理量的漂移不超过0.5 kPa。综上所述，采用多点k 执行修正方法可适应的传感器漂移范围更广，与标定基准值测量误差更小。

新标定方法矫正了传感器测量值与基准值的测量误差，同时保证两者变化趋势的一致性，能较好地解决氧气成分测量正确性的问题。虽然测量灵敏度精度略有下降，但满足使用要求，是延长使用氧传感器寿命的有效方法。

4 结束语

本文分析了密闭舱内氧气测量传感器变化特性，运用多传感器数据融合方法确定传感器自动标定基准值，并提出一种改进的传感器标定方法。该方法可有效缩短传感器标定频次，降低系统运行风险，对处于寿命末期的氧传感器，其适应范围更广，测量误差更小，为氧传感器自动标定、延寿使用提供有效的参考。