空间站梦天实验舱整器动力学分析和试验研究

吴 松，陈燕毫，刘 芳，柏合民，唐国安

（1.复旦大学 航空航天系 上海 200433；2.上海宇航系统工程研究所，上海 201109）

0 引言

中国空间站被命名为“天宫”，是中国航天“三步走”战略最重要的目标［1］。“天宫”空间站基本构型包括“天和”核心舱、“问天”实验舱和“梦天”实验舱。空间站舱段、单机设备等在发射、入轨、在轨服役期间会经历严峻的动力学考验，在研制阶段必须充分考虑任务阶段内的各种动力学问题，在设计时需要预示整体结构的动态响应、辨识载荷和结构特性、分析系统稳定性、控制振动和噪声等，其中有不少问题是基于整器级的动力学模型开展动态分析而得到解决［2］。然而，开展动态特性分析的数学模型为实际结构的简化描述，往往与真实结构存在一定差异，根据数学模型去进行动态响应预示、控制和优化工作，可能会产生较大分析误差，甚至会颠覆设计方案，因此，整器级模态试验与环境试验项目（验收级试验、鉴定级试验等），是航天器研制过程中必不可少的试验项目，对获取准确的动力学特性有重要意义。

空间站梦天实验舱总高度约18 m，质量超过20 000 kg，由多个舱段组成且由不同单位牵头负责研制，为了在研制初期能够准确预示实验舱整器动力学特性，可依据不同舱段的动力学试验结果，考虑舱段连接界面的连接刚度，采用动态子结构方法，预示整器动力学特性［3-4］。同时，由于空间站各舱段连接构型具有一定相似性，在验证子结构综合预示方法精度后，在后续其他航天器型号中，只需要进行部件级模态试验，可节省经费，缩短研发周期。

基于“化整为零，积零为整”的基本思想，根据不同的子结构界面自由度处理方式，动态子结构方法可被划分为混合界面模态综合法、自由界面模态综合法以及固定界面模态综合法［5-6］。在固定界面模态综合法中，界面被约束，不存在零频刚体模态，采用子结构的低阶模态信息表示组合体的高阶模态信息时，避免了刚体模态引起的刚度矩阵奇异不便于求解的问题。在计算低阶模态信息时，基于固定界面模态综合法发展而来的Craig-Bampton-Hurty（CBH）方法［7-8］具有较高的求解精度，同时方法简单，便于编程实现。为了解决复杂工程问题，大量学者对CBH 方法的实际应用开展了深入研究［9］。基于CBH 方法，史纪鑫［10］对包含柔性太阳电池翼的航天器开展了动力学研究。邓峰岩［11］等将CBH 方法应用到多体动力学研究中，取得了一定成果。多位学者利用CBH 方法，在多体动力学领域解决了众多难题，例如保持架的柔体动力学模型［12］、波轮式洗衣机刚柔耦合模型［13］以及直升机起落架测试系统的刚柔耦合动力学模型。文献［14］将连接界面刚度展开成泰勒级数，基于力平衡和位移协调条件，解决了CBH 方法中高阶截断模态带来的计算误差问题。文献［15］基于部件级模态信息，分析了四机并联发动机低频动力学特性，避免了发动机与机架的低频脉动及箭体振动耦合难题。在航天领域，通常将运载火箭简化为梁模型，将火箭发动机、整流罩、飞行器等作为子结构［16］。文献［17］计算了二级发动机、整流罩和卫星的自由—自由界面子结构模态信息以及一级发动机的自由—固定界面子结构模态信息，基于模态混合综合方法，计算得到整个系统的模态，与有限元模型低频计算结果的误差小于1%。文献［18］将整流罩、被发射载荷分别作为子结构1 和子结构2，其中，子结构1 基于有限元仿真方法得到模态，子结构2 采用试验方法得到模态，模态综合后得到了整流罩-被发射载荷系统的模态信息。文献［19］将飞船振动台试验系统的复杂问题简化为若干个小系统，对每个小系统进行充分的仿真分析和模型修正，组合成下一级系统，再次增加新的经过修正的小系统，逐级修正和验证，得到整体系统的仿真模型。

部件之间的连接关系、边界条件对于系统的动力学特性影响较大［20］。为简化连接关系，部分学者在动力学计算模型中将各个部件间的连接关系视为刚性连接［21］，计算模型中连接关系的处理与结构实际连接关系的差异，会导致计算结果与测试结果的巨大误差。将部件连接关系视为柔性连接，能够在一定程度上降低计算误差［22-23］。黄修长等［24］将位于浮筏和舱体之间的隔振器用弹簧和阻尼等效，计算结果与测试结果具有一致性。但是，在大部分结构中，连接关系复杂，难以得到刚度和阻尼参数，将连接关系等效为刚度和阻尼的方法具有较大的局限性。

针对上述问题，李志深等［25］对子结构综合法进行了改进，提出了连接单元虚阻抗（Virtual Joint）的概念。根据整体结构和子结构的频响逆向得到连接特性，并采用阻抗矩阵的形式表征连接关系对结构动力学特性的影响。采用上述方法，计算了铣刀系统的动力学特性，结果表明，与传统的子结构综合法相比，该方法能够得到与实际结构更为吻合的结果。

本文针对空间站梦天实验舱的整器模态预示，通过建立舱段间连接结构的详细模型，考虑连接结构接触非线性影响，构建连接结构的合理等效模型，采用子结构模态综合方法，计算整器基频，通过整器模态试验，验证基于连接结构模型的子结构综合预示方法的准确性，指导后续空间站其他航天器型号研制，为缩减整器级模态试验提供支撑。

1 梦天实验舱整器模态综合方程

1.1 总体构型

梦天实验舱构型如图1 所示，包含子结构a 和子结构b 两个舱段，总长约20 m，发射质量达22 000 kg［26］。其中，子结构a与试验工装、子结构a与子结构b 之间均通过144 个M10 螺栓进行连接。法兰与螺栓的连接如图2 所示。

图2 舱段间的连接法兰Fig.2 Connecting flanges between the cabin compartments

1.2 子结构划分

根据实验舱构型特点，整器可划分为子结构a、子结构b 两个子结构，如图3 所示。约定整器模型上，子结构a 与试验工装之间的连接刚度记为kn，共有144 个螺栓，故n取值为1～144，子结构a 上的连接点编号记为1～144；子结构a 和子结构b 之间的连接刚度记为km，共有144 个螺栓，m取值为1～144，其中子结构a 上的连接点编号记为145～288，子结构b 上的连接点编号记为289～432。

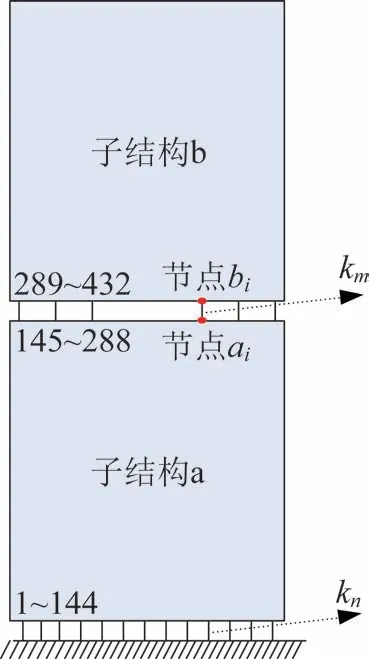
图3 子结构构型Fig.3 Schematic diagram of substructure configuration

1.3 系统动力学方程

将每个螺栓连接点定义为缩聚模型的外部节点，则子结构a 截断后的质量阵和刚度阵分别为

式中：M、K分别为质量矩阵和刚度矩阵；下表a、b分别代表子结构a 和子结构b；下标1 表示子结构a与试验工装之间连接螺栓的外部界面自由度；下标2 表示子结构a 与子结构b 之间连接螺栓的外部界面自由度；L1为子结构a与试验工装之间连接螺栓数量；L2为子结构a 与子结构b 之间连接螺栓数量；q1为子结构a 缩聚模型的广义坐标；Na为子结构a界面固支边界下的模态截断阶数。

截断后，子结构b 刚度阵和质量矩阵分别为

式中，下标3 表示子结构b 与子结构a 之间连接螺栓的外部界面自由度；q2为子结构b 缩聚模型的广义坐标；Nb为子结构b 模态截断阶数。

若不考虑子结构a 与试验工装以及子结构a 和子结构b 间连接时，对子结构a 和子结构b 进行组装，则子结构a、b 组合体的质量矩阵和刚度矩阵分别为

在计算螺栓连接刚度时，由于螺栓质量相对实验舱整舱质量可以忽略，仅需考虑其连接刚度的作用。两个子结构间的螺栓刚度矩阵为

式中：k为刚度大小，下标Tx、Ty、Tz和Rx、Ry、Rz分别为3 个平动和转动方向。

则子结构a 和子结构b 连接界面的刚度矩阵可以写为：

因此，考虑子结构a 和子结构b 间的连接刚度时，实验舱整舱根部固支边界下的刚度矩阵为

进一步计及子结构a 和试验工装间的连接刚度对整器的影响。首先记子结构a 和试验工装间单个螺栓的刚度为

式中：k′与k含义一致，均表示刚度大小，但由于螺栓不同导致数值可能不同。则子结构a 和与试验工装连接界面的螺栓连接刚度矩阵可以写为

因此，同时计及子结构a 与试验工装、子结构a和子结构b 之间的连接刚度时，实验舱整舱固支边 界下的结构刚度矩阵为

而质量矩阵不变，此时，实验舱整舱根部固支状态的动力学特征值方程为

式中：λ为广义特征值；φ为广义特征值对应的特征向量。

基于式（15）可依据子结构分舱段模态试验结果，根据子结构a 与试验工装、子结构a 与子结构b之间的连接刚度，可实现准确预示实验舱整舱的基频。

2 螺栓法兰连接刚度分析

螺栓法兰连接结构在轴向荷载下的变形及应力分布，呈现出轴向拉压刚度双线性的特征。结合梦天实验舱连接界面的特点，其整体横向刚度主要通过单个螺栓承受轴向拉压载荷提供，同时由于相邻螺栓跨距较大，忽略螺栓间的相互耦合作用。因此，可采用等效轴向弹簧模型来模拟连接界面的刚度。

等效弹簧的轴向拉压刚度，可通过对单个螺栓法兰结构进行详细建模、计算得到。根据单个螺栓法兰的设计参数，建立详细的有限元模型。

2.1 轴向拉刚度

依据单个螺栓法兰沿轴向的拉载荷传递路径以及对称性假设，分别确定约束边界和载荷施加点位置，如图4 所示。根据该分析模型，考虑法兰、螺柱、螺母和垫片之间相互接触以及螺栓预紧力的影响，分级施加外载荷，计算螺栓法兰的位移大小，变化曲线如图5 所示。

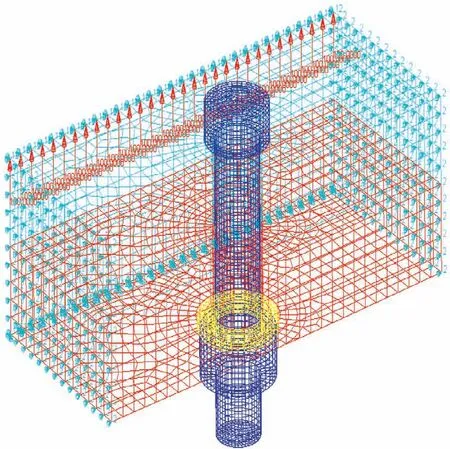
图4 拉刚度计算模型Fig.4 Model for tensile stiffness calculation

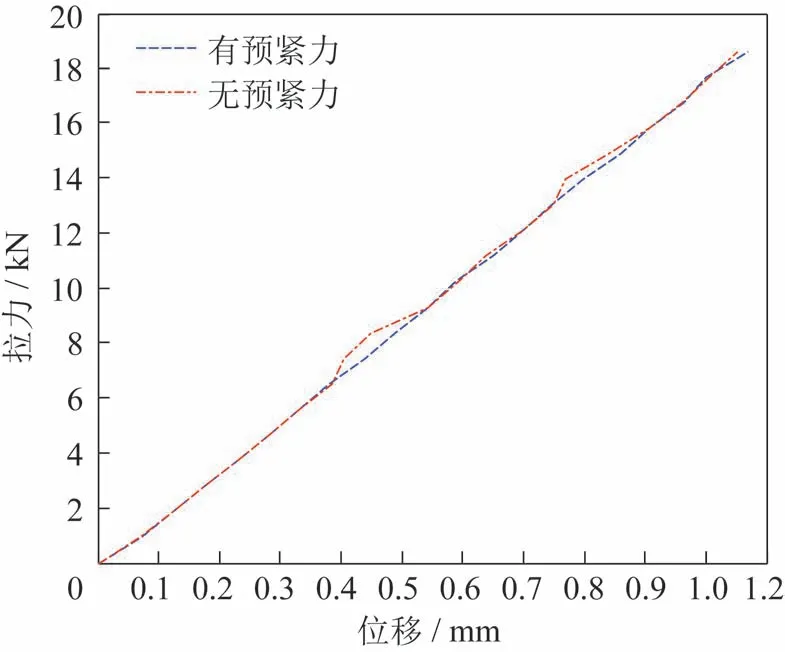
图5 单个螺栓的位移随拉力的变化曲线Fig.5 Variation curve of the displacement of one bolt with the tensile force

由图5 可知，单个螺栓法兰结构在轴向拉载荷作用下，位移随外载荷变化的线性度较好，并且有无预紧力影响不大。经分析曲线拟合得到单个螺栓的轴向拉刚度为Kl=1.741×107N/m。

2.2 轴向压刚度

依据单个螺栓法兰沿轴向的压载荷传递路径以及对称性假设，分别确定约束边界和载荷施加点位置，如图6 所示。根据该分析模型，考虑法兰、螺柱、螺母和垫片之间相互接触以及螺栓预紧力的影响，分级施加外载荷，计算螺栓法兰的位移大小，变化曲线如图7 所示。

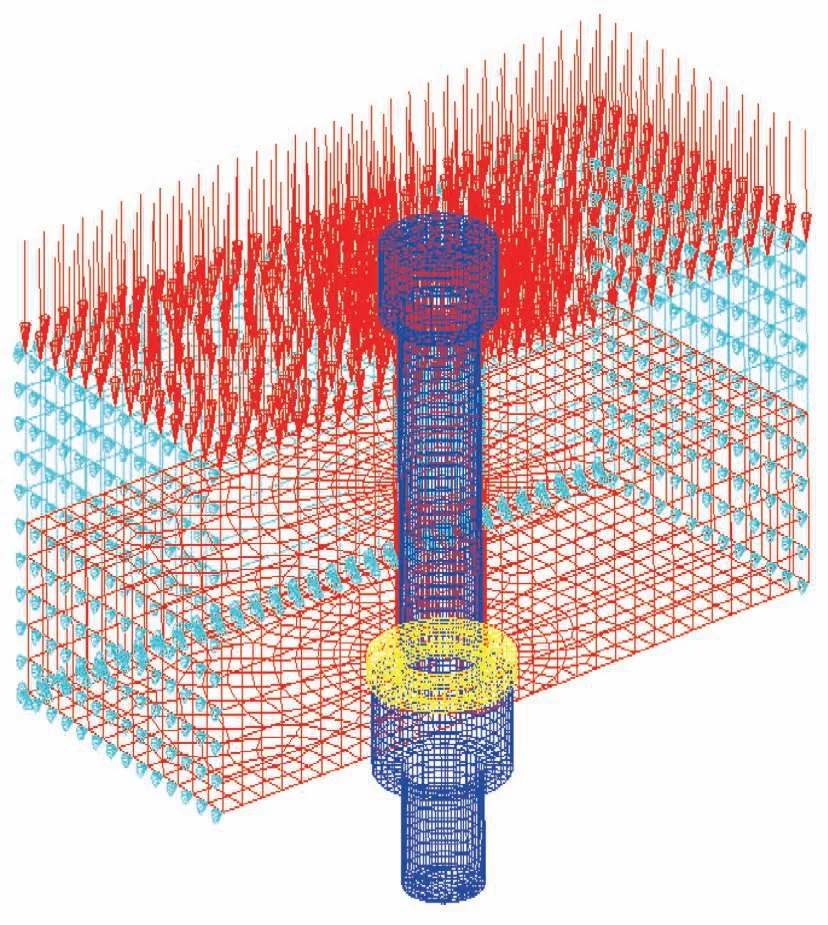
图6 压刚度计算模型Fig.6 Model for compression stiffness calculation

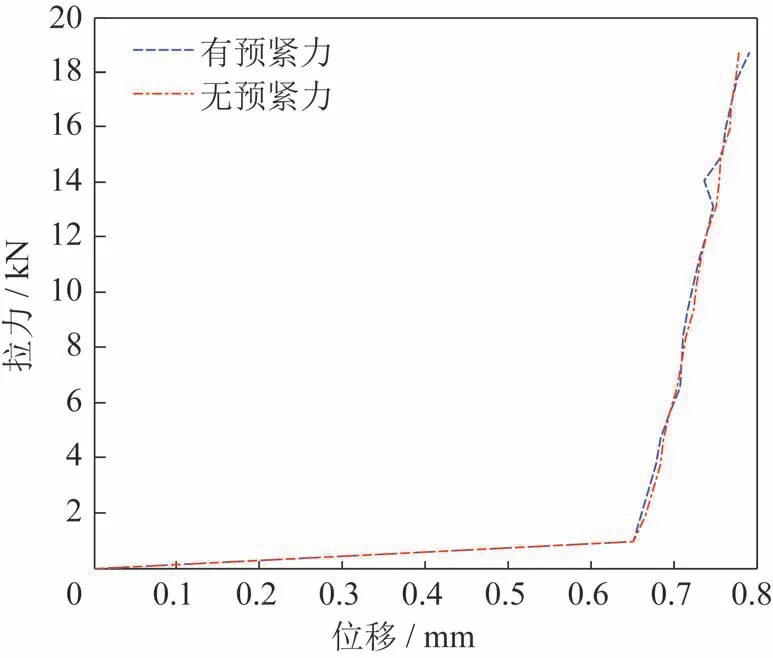
图7 单个螺栓的位移随压力的变化曲线Fig.7 Displacement Curve of bolt with pressure

由以上分析可知，单个螺栓的轴向压刚度与有无预紧力影响不大，且在外载荷小幅增加后，刚度呈现突变特性。经曲线拟合得到突变前后，单个螺栓的轴向压刚度分别为Ky1=1.436×106N/m，Ky2=1.278 5×108N/m。考虑到梦天实验舱典型工况中单个螺栓载荷远大于1.0 kN，故后续分析中单个螺栓压刚度取为Ky=1.278 5×108N/m。

3 分舱段模态试验

梦天实验舱主要由4 个舱段组成，分别是工作舱、气闸舱、载荷舱和资源舱，如图8 所示。

砖子不吭声，他不知如何吭声，他从反馈的消息得知，这次赵仙童确实没有李金枝演得好，那是一锤定音的事，谁也改变不了的，除非下次再去摘。他也明白，摘梅花是多少戏人的终极追求，赵仙童例外不了。可命运女神是不会光顾每一个求梦者的，这就是现实，残酷的现实啊。

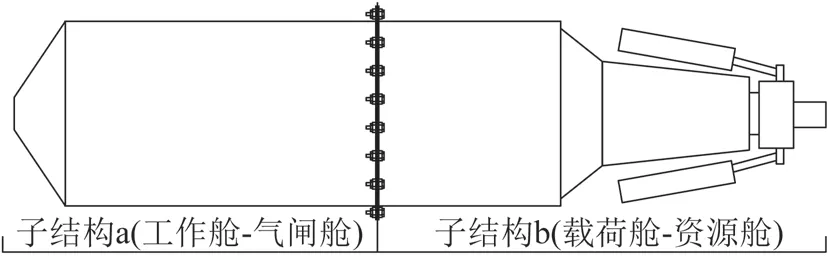
图8 梦天实验舱分舱段Fig.8 Schematic diagram of the Mengtian lab module

根据结构连接特性，工作舱、气闸舱作为子结构a 参与动力学计算和试验，载荷舱、资源舱作为子结构b 参与动力学计算和试验，如图9 所示。

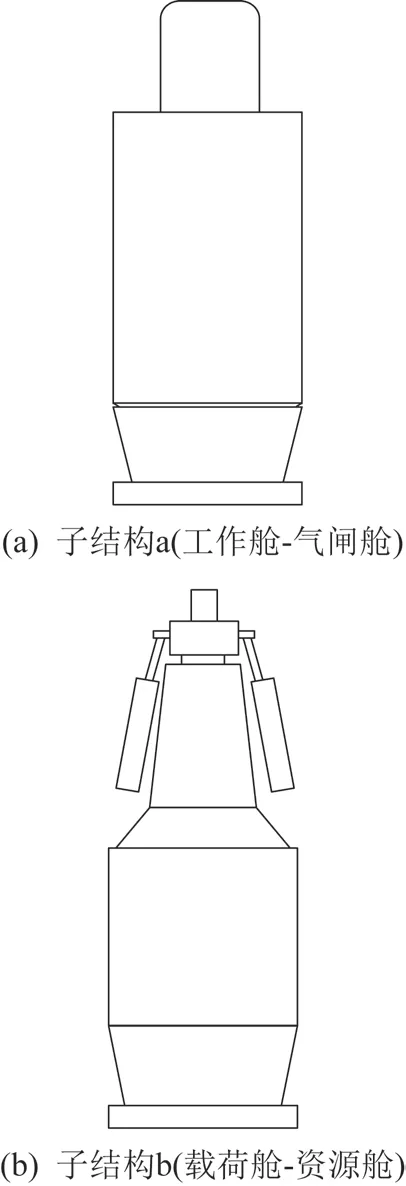
图9 子结构a 和子结构bFig.9 Schematic diagram of Substructure a and Substructure b

3.1 子结构a 模态试验及修正

针对子结构a 开展模态试验，辨识其动力学特性，模态试验如图10 所示。

图10 子结构a（工作舱-气闸舱）模态试验Fig.10 Modal test of Substructure a（working cabincargo airlock cabin）

基于子结构a 的模态试验结果，对子结构a 分析模型进行修正，修正后分析及试验主要频率见表1。

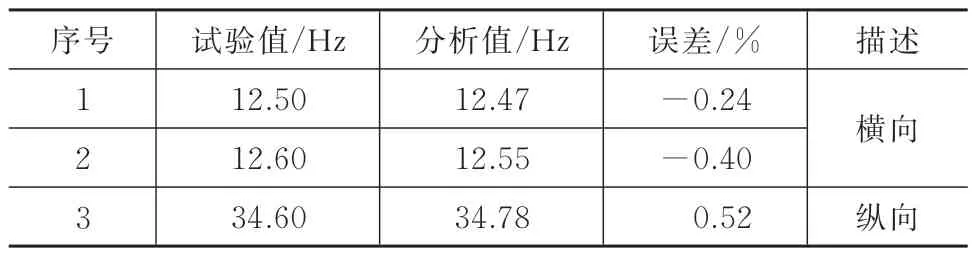
表1 子结构a 主要频率实测与修正后分析值Tab.1 Measured and analysis results of the main frequencies of Substructure a

3.2 子结构b 模态试验及修正

针对子结构b 开展模态试验，辨识其动力学特性，如图11 所示。

图11 子结构b（载荷舱-资源舱）模态试验Fig.11 Modal test of Substructure b（load cabin-resource cabin）

基于子结构b 的模态试验结果，对子结构b 分析模型进行修正，修正后分析及试验主要频率见表2。

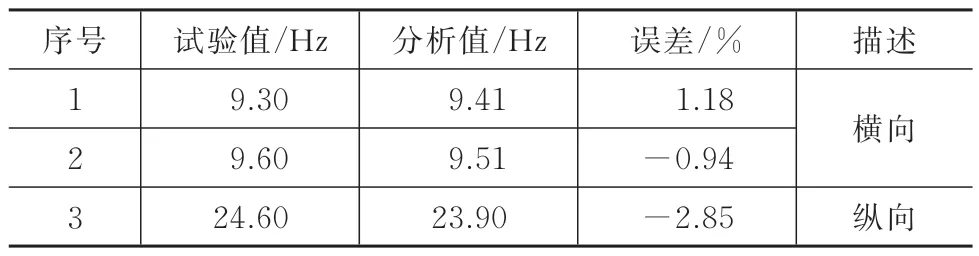
表2 子结构b 主要频率实测与修正后分析值Tab.2 Measured and analysis results of the main frequencies of Substructure b

4 整器模态预示

梦天实验舱在发射过程中承受了轴拉、轴压和横向等多种载荷的共同作用，螺栓法兰连接点处呈现或拉或压的受力状态。由之前的分析可知，螺栓法兰的连接刚度与拉压状态显著相关，呈现典型的拉压刚度突变特征，导致梦天实验舱整器基频实际在某个窄带内小幅波动。

依据舱段间的螺栓连接刚度分析，定义如下几个典型状态，进行分析预示。状态1：考虑螺栓连接刚度为无穷大；状态2：所有连接螺栓均处于受压状态；状态3：所有连接螺栓均处于受拉状态；状态4：一侧72 个螺栓处于受压状态，另一侧72 个螺栓处于受压状态；状态5：一侧96 个螺栓处于受压状态，另一侧48 个螺栓处于受压状态。

依据修正后子结构a、子结构b 有限元模型的缩聚质量和刚度矩阵，以及连接面间的螺栓连接刚度，基于式（15）预示不同状态下梦天实验舱整器的主要频率，分析预示结果见表3。

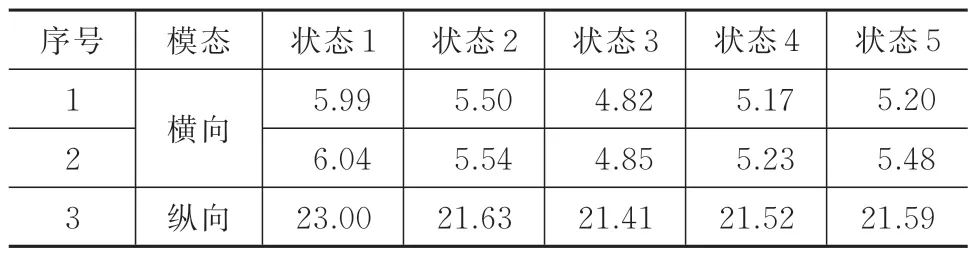
表3 不同螺栓拉压状态下梦天实验舱整器主要频率预示结果Tab.3 Predicted results of the main frequencies（Hz）of the Mengtian lab module under different bolt tensile and compressive conditions

5 整器模态试验及对比分析

针对梦天实验舱组合体状态开展模态试验，辨识其动力学特性，模态试验如图12 所示。

图12 梦天整器模态试验Fig.12 Modal test of the Mengtian lab module

考虑不同连接结构的等效刚度建模方式，采用子结构模态综合方法，梦天实验舱整器主要频率预示与实测结果对比见表4。

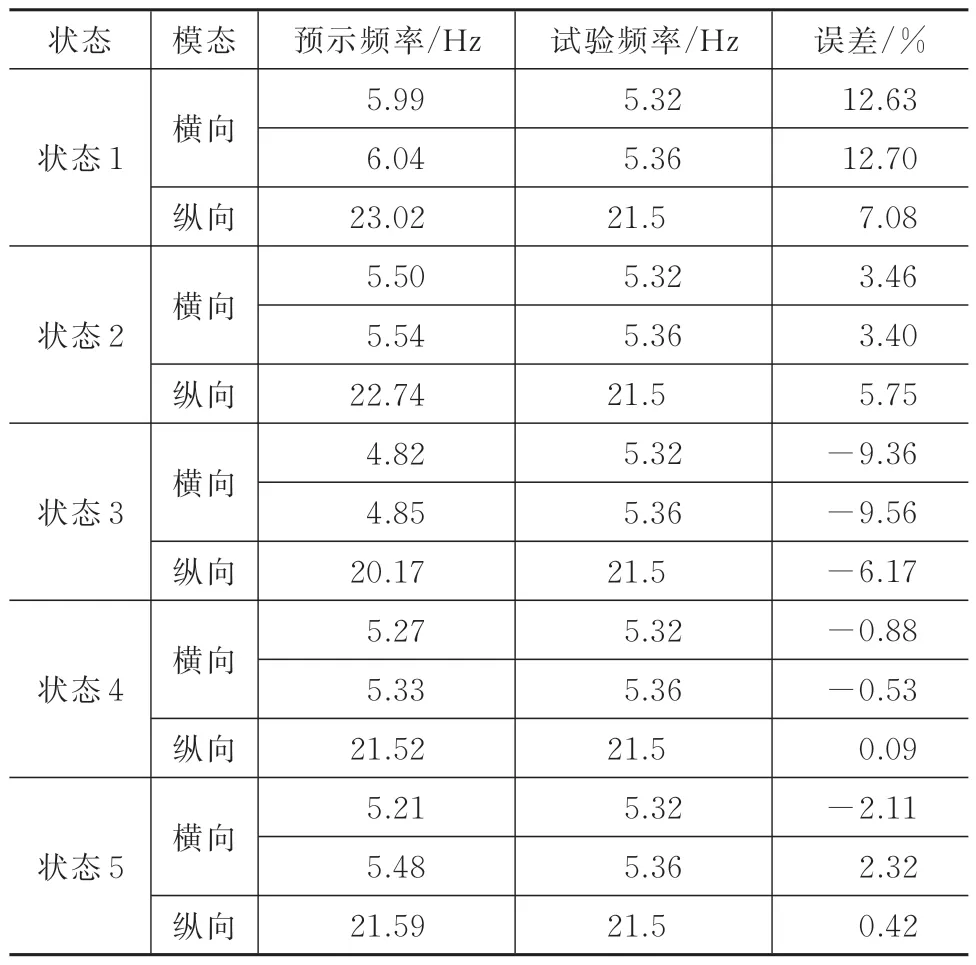
表4 梦天整器主要频率预示与实测对比Tab.4 Comparison of the predicted and measured results of the main frequencies of the Mengtian lab module

由表4 可知，①将螺栓连接考虑为刚性的整器预示频率横向偏高约12.6%，纵向偏高约7%；② 仅考虑螺栓压刚度的整器预示频率横向偏高约3.5%，纵向偏高约5.7%；③仅考虑螺栓拉刚度的整器预示频率横向偏低约9.4%，纵向偏低约6.2%；④ 同时考虑螺栓拉和压刚度的整器预示频率与试验频率比较接近，其中受拉和受压螺栓数量各一半的预示频率横向偏低约0.5%，纵向偏高约0.1%，受拉和受压螺栓数量分别为三分之一和三分之二时的预示频率横向误差为2.3%，纵向误差约0.4%。

6 结束语

1）空间站大型航天器舱段间的连接刚度对整器主要频率有较大影响，刚性连接处理时整器主要频率偏高达12%。

2）整器各向基频的实测结果介于考虑螺栓仅为拉和仅为压刚度的预示结果之间，并与同时考虑螺栓拉和压刚度的预示频率与试验频率接近。

3）通过合理划分子结构舱段，同时考虑螺栓法兰结构受拉和受压的数量时，整器模态主要频率综合预示结果与实测值误差小于3%，能够满足工程型号研制需求，实现缩减大型航天器整器级模态试验的目的。