梦天实验舱初始轨道快速计算策略与分析

段成林，盛庆轩，段建锋，王浩宇，慎千慧，陈 铭

（北京航天飞行控制中心，北京 100094）

0 引言

航天器的初始轨道是判断航天器是否入轨的重要判据，也是航天器入轨异常时应急控制计算的必要条件。梦天试验舱是组成中国空间站基本构型的3 个舱段之一，也是中国空间站第二个科学试验舱［1］。梦天舱入轨时可用于确定初始轨道的数据源包括火箭遥测数据、实验舱遥测全球导航卫星系统（Global Navigation Satellite System，GNSS）数据，以及实验舱入轨后的外测USB 数据，其中火箭遥测数据包括箭遥GNSS 数据［2-4］和箭遥惯组数据［5-6］。一般情况下，使用火箭遥测数据进行初轨计算时，通常使用舱箭分离前最后一帧数据，通过预设的理论分离速度和角度计算舱箭分离时刻的试验舱初始轨道［7-9］；舱遥GNSS 数据覆盖了舱箭分离前后全部时间段，由于定位精度较高，是确定试验舱初始轨道的主要数据源；外测数据［10-12］是试验舱入轨后的重要备份测控手段，具有较高的测量精度，也是初轨计算的主要来源之一。

梦天试验舱由运载火箭发射入轨并舱箭分离后，传统初始轨道计算通常有2 种策略：1）使用舱箭分离前后1 点或多点火箭遥测数据、实验舱遥测和外测数据计算多组初始轨道，分析计算各初始轨道与理论轨道的偏差，根据经验选择其中一组数据源计算结果作为试验舱初始轨道。使用该策略，火箭入轨后即可快速计算出初始轨道，由于使用数据点数较少，且预设的理论分离速度、角度与真实状态有所不同，初始轨道精度与实际轨道可能会有较大偏差。2）累积分离后一定时长的实验舱遥测GNSS 或外测数据，进行事后精密轨道确定，如果定轨结果与其他数据源一致，可直接将事后定轨结果优选为初始轨道。使用该策略，优点是计算结果精度高，缺点是初轨计算耗时较长［13-15］。

针对传统初始轨道计算时间与精度不能兼顾的问题，本文设计了初始轨道快速计算及优选判断策略。首先根据运载火箭加速度变化获取舱箭分离时间；其次采用基于动力学约束的实时轨道滑动［16-18］批处理方法累积超短弧分离后数据计算初始轨道；最后对利用各种数据源确定的多组初始轨道进行逻辑优选判断，提高了精度和效率，可应用到空间站工程后续各航天器入轨后初始轨道快速计算时使用。

1 舱箭分离时间判断

航天器初始轨道的历元时间一般选择在器箭分离时刻，准确及时估计器箭分离时间是初始轨道计算的前提。梦天试验舱由长征五号B 遥四运载火箭在文昌航天发射场发射升空，运载火箭起飞后，在一二分离、舱箭分离时，火箭的加速度会发生剧烈变化，通过加速度变化可以准确估算各关键事件发生时间。

计算分离时间时，在舱箭分离前分别使用各类遥测GNSS 数据和惯组数据实时计算火箭加速度，比较上一时刻求得的加速度与当前时刻加速度，若比值超过事先设定的阈值，则认为该数据源判断出舱箭分离。为了避免误判，可事先设定至少2 类数据源同时判断舱箭分离，且每个分离时间在运载火箭最大理论分离时间偏差范围内才认为事件发生。判断时设定的加速度变化阈值与火箭型号有关，可事先通过仿真或相关火箭实测数据模拟计算获取。计算火箭加速度时，依据飞行时序，采用动态滑窗方法对火箭速度进行多项式拟合，其1 阶拟合系数即为加速度。判断舱箭分离后，舱箭分离时间取滑动窗口中心时刻。分析表明，选用3 阶多项式即可达到很好的逼近效果。在实际计算过程中，可适度调整多项式阶数和滑动窗口的宽度，以满足时间要求和精度要求。

如果有多种数据源计算得到不同的分离时间，可通过如下方法计算最终的分离时间。

步骤1设获取到的分离时间为n个，由于不同数据源测量精度和体制差异，可设置其判断权重分别为λi，(i=1，2，…，n)。对各数据源权重进行归一化处理。设处理后各数据源获取的分离时间权重为，(i=1，2，…，n)，如式（1）所示：

步骤2设各数据源计算的分离时间为ti，(i=1，2，…，n)，设平均分离时间为，如式（2）所示：

步骤3计算各分离时间距平均分离时间的方差。设各分离时间距平均分离时间的方差为εi，如式（3）所示：

步骤4根据各分离时间距平均分离时间的方差大小，动态调整各数据源的新权重。记各数据源的方差和为εa，如式（4）所示：

步骤5重复步骤2、3、4，直至在步骤4 的计算中，当某条数据源的新权重大于50%时，该数据源计算的分离时间即为最终计算分离时间。特殊情况，如果只有2 类数据源判断分离时间，则计算这2类分离时间的均值为最终分离时间。

本文舱箭分离时间判断采用多组计算结果逐次迭代取方差最小的数据源的优选方法。每次迭代前加权计算所有分离时间的均值，然后根据各分离时间距平均分离时间的方差，动态计算各数据源的新权重，重复迭代过程，直至某条数据源的新权重大于50%时终止。由于在逐次迭代过程中，方差最大的数据源权重不断降低，方差最小的数据源权重越来越大，迭代结束时最终选择的分离时间，一定为集群计算结果中方差最小的那条数据源计算的结果，保证了分离时间计算的的可靠性和精度。

2 实时轨道滑动批处理算法

2.1 算法原理

实时轨道滑动批处理算法将事后精密轨道确定方法实时化。该算法接收外部初值，在试验舱入轨后积累数据进行最小二乘拟合，根据测量数据迭代改进初值，解算出一组与测量数据残差平方、最小的精确轨道，并将该轨道作为新的计算初值，继续接收新的测量数据，进行下一次计算。当累积数据数量或时长超过事先设定值后，采用动态滑窗方法进行处理。该算法通过增加动力学约束将每个时刻目标的位置和速度的估计问题，转化为滑动窗口特定时刻目标的位置和速度的估计问题，极大减少了待估参数数量［19-21］。随着观测数据的逐步累积，实时轨道计算精度逐渐逼近事后精密轨道确定精度，轨道计算稳定性也有了大幅度提高。该算法处理流程如图1 所示。

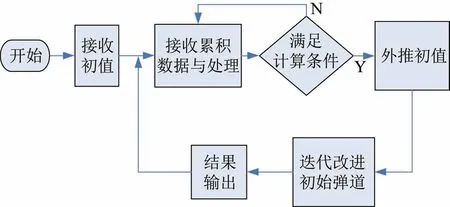
图1 实时轨道滑动批处理算法处理流程Fig.1 Procedure of the real-time orbit sliding batch algorithm

2.2 动力学模型

航天器的考威尔积分运动方程［24-26］为

式中：r为航天器t时刻的位置坐标列向量；p为模型参数向量；r0、分别为探测器在J2000.0惯性坐标系中某历元时刻的位置和速度，p*为与阻力、引力谐系数、测量系统差等有关的常值模型参数。

使用动力学模型进行轨道改进时，首先计算探测器总的摄动加速度，获取探测器的理论轨道；然后使用理论轨道反算观测量并与实际测量值做差，采用最小二乘方法使得差的平方和最小。在此过程中，探测器t时刻位置速度参数r0，、模型参数p*等作为未知参数一起被求解。

2.3 测量模型

轨道确定的基本过程是对来自测量模型的参数估值进行微分改正，使得原始观测数据与模型计算理论值的差加权平方和为最小。观测数据的测量模型可以表示为

式中：t为观测数据时间；δt为时间系统差；X、为航天器在J 2000.0 惯性坐标系下位置和速度参数；p为动力学模型参数向量，包括航天器初始状态参数、引力场系数、阻尼系数等有关变量；R为测站惯性系下的坐标；b为测量数据系统误差；ε为测量数据随机误差，包括大气折射、应答机时延、天线坐标误差等。

对于近地航天器，待估计的模型参数为p，R，b，δt。

2.4 估计模型

测量方程是非线性的，可以使用一阶泰勒展开进行线性化处理。这种处理建立了观测数据残差中的偏差与动力学参数、站址、观测系统误差，以及时间系统偏差之间的关系，如式（8）所示：

式中：Y为实际观测量；Yc为理论观测量；e为观测白噪声；为测量方程偏导数，由观测量偏导数和状态转移偏导数两部分组成；σ为总的待估计参数，包括动力学参数p、站址R、观测系统差b以及观测时间系统差δt。

设总的估计参数σ表示为

则测量方程可进一步表示为

2.5 状态方程

航天器有摄状态运动方程是非线性化的，可以写成：

式中：X为航天器在t时刻的位置速度状态量；为其一阶导数。

如果已知初始值X0，泰勒展开取一阶项，可以得到以下线性方程：

这是一个系数依赖于时间的线性微分方程系统，可以表示为

式中：矩阵Φ(t，tk)称为状态转移矩阵，Xk是航天器在tk时刻的位置速度状态量。

其初始条件Φ(t，tk)=I，I为单位矩阵。X(T)为航天器在T时刻的位置速度状态量，X0为航天器在t0时刻的初始位置速度状态量，

由时刻t0至时刻T时，状态转移矩阵的元素为

由初始状态时刻t0外推至时刻T，有：

Φ(T，t0)可使用数值积分对运动方程的变分方程积分得到。

3 仿真及结果分析

3.1 初始条件设置

为验证舱箭分离时间和实时滑动批处理算法的精度，采用梦天实验舱主动段理论弹道，模拟起飞过程，并计算入轨后初始轨道。理论弹道速度曲线如图2 所示。各类遥外测数据标称误差设置见表1。

图2 梦天试验舱主动段速度曲线Fig.2 Velocity curve of the active section of the Mengtian lab module

根据以上条件，采用1 倍标称测量误差，进行100 次Monte Carlo 仿真，分析计算舱箭分离时间和初始轨道的精度。

3.2 舱箭分离时间分析

计算舱箭分离时间时，根据主动段理论弹道计算运载火箭加速度，如图3 所示。由图3 中可知，运载火箭在一二级分离和舱箭分离时，加速度均出现了阶跃性变化。其中，舱箭分离时，加速度从超过20 m/s 迅速降为1 m/s 以下。据此，可设置舱箭分离判断条件为：火箭飞行时间大于400 s 且加速度变化率大于10 m/s3。

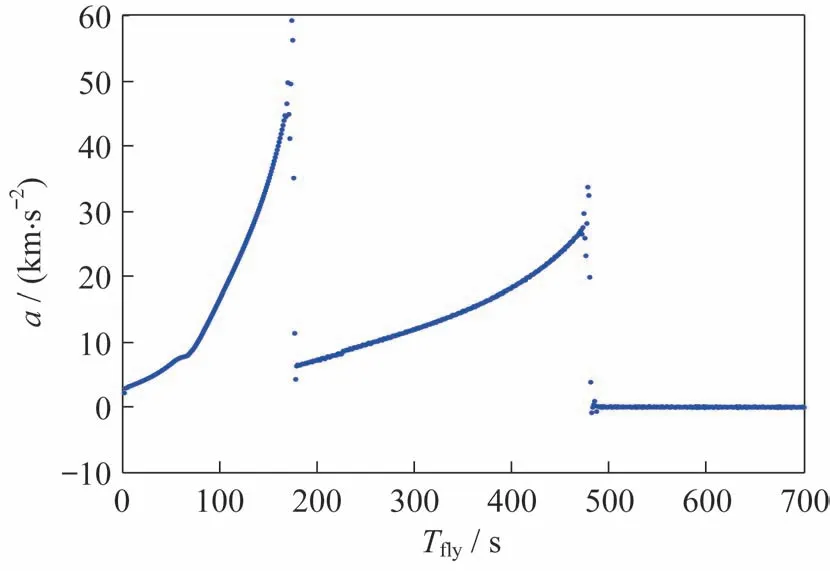
图3 梦天舱运载火箭加速度变化曲线Fig.3 Acceleration variation curve of the launch vehicle with the Mengtian lab module

采用100 次Monte Carlo 打靶仿真，根据加速度变化计算舱箭分离时间和理论分离时间偏差，如图4 所示。其中，横轴为仿真次数，纵轴为分离时间偏差。

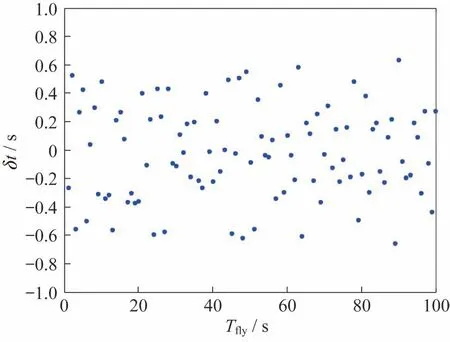
图4 Monte Carlo 仿真和理论计算打靶舱箭分离时间偏差Fig.4 Deviation of module and arrow separation time obtained by Monte Carlo simulation and theoretical calculation

由图4 可知，根据加速度变率计算得到的舱箭分离时间和理论分离时间的偏差在0.5 s 以内。实际任务中，初始轨道计算时，如果器箭分离后测控系统判断出实际的分离时间，则以实际分离时间为准；其他情况下，可以采用本方法计算的分离时间，精度满足任务要求。

3.3 实时初始轨道计算精度分析

获取到舱箭分离时间后，批处理算法开始累积器遥GNSS 和外测USB 数据，分别计算初始轨道，历元时间固定为舱箭分离时间。初始轨道与事后精密轨道在器箭分离时刻的位置、速度偏差如图5所示，纵轴为批处理算法数据累积时长，横轴为位置或速度偏差。其中，精密轨道使用分离后30 min器遥GNSS 数据的定轨结果。

图5 初始轨道位置、速度偏差Fig.5 Position and velocity deviations of the initial orbit

由图5 可知，使用器遥GNSS 数据和外测USB数据，批处理算法均能在累积5 s 数据后计算出初始轨道，数据累积超过40 s 后，位置、速度误差均趋于稳定。其中，使用器遥GNSS 数据，位置偏差稳定在4.5 m、速度偏差稳定在0.05 m/s 以内；使用外测USB 数据，位置偏差稳定在300 m、速度偏差稳定在2 m/s 以内。

综上，在各类数据正常的情况下，设置梦天舱入轨后批处理累积40 s 数据计算结果作为优选初始轨道，可达到与事后精密轨道同等精度，而时效性远超事后确定精密轨道。

4 结束语

本文针对在舱箭分离后航天器传统初始轨道计算中时间与精度不能兼顾的问题，设计了初始轨道快速计算策略，根据运载火箭加速度变化来判断舱箭分离，采用实时轨道滑动批处理方法累积超短弧分离后数据计算初始轨道。通过仿真数据分析，得出如下结论：

1）通过运载火箭加速度变化率来计算舱箭分离时间，时间偏差在0.8 s 以内，满足任务需求。

2）采用实时轨道滑动批处理方法计算初始轨道，耗时控制在1 min 以内，初始轨道精度与事后精密定轨精度保持一致，时效性远超事后精密轨道确定方法。