基于Lyapunov-MARC 算法的矿用乳化液配比方法分析

范抑伶

（唐山学院智能与信息工程学院， 河北 唐山 063000）

0 引言

乳化液作为综采面液压设备的压力源，其配比浓度会直接影响液压支架的工作性能和使用效果[1]。乳化液浓度过高则会提高生产成本，反之，则会大幅度降低液压元件的润滑性、防锈性和稳定性，从而影响设备寿命和安全生产。因此设计一个准确、稳定、快速、高效的乳化液自动配比系统是非常重要的。目前，国外对于矿用乳化液的配比技术多采用离散式的控制方法，如雷波公司所采用的分布式多泵叠加乳化液配比控制方法。而国内针对乳化液配比控制技术主要有以下几类方法，文献[2]提出了一种双缸定比的乳化液自动配比系统，该方法通过利用双作用油缸活塞和活塞杆面积的固定比值关系，实现乳化油和水定量定比供给，但是，该方法没有反馈环节，机械机构复杂，且不能够连续调整乳化液的配比浓度；文献[3]提出了一种以井下压风为动力的自动配液装置，这种配比系统操作繁琐，受到井下水压、风压变化的影响，浓度无法在线调节，由此配比的精度无法保证；另外，还有相关研究人员利用模糊控制理论以及PID 控制等方法来实现矿用乳化液的自动配比[4-7]。

针对现有矿用乳化液配比方法存在的各类问题，根据已有的乳化液自动配液的理论，结合井下矿用乳化液配液特点，进行电动机与柱塞泵的建模。针对在实际工程应用中，柱塞泵动态响应滞缓导致流量精度不准的问题，提出利用Lyapunov-MARC 自适应控制方法对乳化液配比进行控制的方法。

1 油路柱塞泵流量模型分析

乳化油密度受温度影响，将温度对油路的影响考虑在内，为此经过大量的实验数据采集并进行整理分析后，可得到如表1 所示的乳化油浓度/温度数据表。

井下工作面作业温度一般在零上几度到二十几度，乳化油油箱中液体温度和环境温度几乎一致，而水的密度随温度的变化微乎其微，因此在设计过程不考虑其密度变化。通过梯度下降算法对乳化液浓度进行线性拟合，实时乳化液浓度（浮化液浓度为浮化液中溶质的质量分数，全文相同）与实时温度线性拟合结果可由公式（1）表示。

式中：x为温度；h（x）为拟合所得的温度- 乳化液浓度函数；拟合所得相关系数为0.902，拟合效果良好，由此利用如公式（1）所示的乳化油密度与温度的函数关系式，在反馈控制结构中加入乳化油随温度变化密度自动调节的模块。

给出所选择的轴向柱塞泵技术参数如表2 所示，将技术参数导入公式（2）所示的理想柱塞泵输出流量模型。

表2 柱塞泵技术参数

式中：A为单个柱塞泵截面面积；ω 为缸体转动角速度；R为柱塞分布圆半径；γ 为柱塞倾角；φi为第i个柱塞泵转角；α 为两个柱塞之间的夹角，其中柱塞泵个数为z的α 计算如公式（3）所示。

通过化简系统，油路系统输入的频率与最终流量呈线性关系，乳化油流量与频率的比值约为0.13655，对油路输出的流量进行积分得到输出油量体积。设计此环节用于模拟延时时间τ，最后进行泰勒展开。通过计算得出柱塞泵理想参考模型的传递函数如公式（4）所示：

实际被控柱塞泵模型的二阶传递函数如公式（5）所示：

式中：ku为变量。由上可得具体乳化液配液控制系统仿真模型如图1 所示。

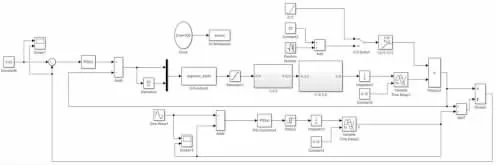
图1 乳化液配液控制系统仿真模型

2 Lyapunov-MRAC 控制器的设计

针对井下环境作用使柱塞泵角速度和流量控制系统的动态响应滞缓的问题，提出基于Lyapunov 稳定性理论的可调增益MRAC 方法控制的乳化液配比方法，求出参数调节的自适应规律，以保证系统的稳定运行[8-9]。图2 为Lyapunov-MRAC 系统结构，设自适应增益γ0/s，参考模型和对象模型的传递函数分别如公式（6）与公式（7）所示：

式中：ku为未知增益，kr、a0、b1与b0均已知，具体大小如公式（4）与公式（5）所示。根据Lyapunov 稳定性理论，计算可调增益的调节式，使被控对象实际输出无限趋近理想模型的输出，即输出误差趋近于零。由图2 可知系统输出误差计算如公式（8）所示：

联立公式（6）、公式（7）与公式（8）可得公式（10）。

式中k计算如公式（11）所示：

对于如公式（12）所示的状态方程：

其中状态向量x可由公式（13）表示：

而Λ、B与c分别可由公式（14）、公式（15）以及公式（16）表示：

若齐次系统=Λx稳定，则存在正定矩阵P和Q满足如公式（17）所示的Lyapunov 方程：

综上可知所设计控制系统Lyapunov 方程可由公式（18）表示：

对式（18）求导可得公式（19）：

为使公式（19）小于零，由此取增益调整律为：

由于控制器执行周期较短，k_u 变化相对较为缓慢，因此其可视为一常数，由此增益自适应律可用公式（21）表示。

由公式（21）可知，增益自适应律受限于状态变量x，由此联立公式（12）与公式（21）可得可调增益自适应律如式（22）所示：

最后结合图2可得系统控制律可如公式（23）所示：

3 系统仿真验证

为验证所设计系统的有效性，首先以方波信号作为输入信号，设置整体仿真时间为10 s，进行如下三组仿真实验。

1）给定流量控制系统幅值r=3 L 方波信号，自适应增益γ0=0.1；

2）保持增益不变，将幅值提高至6 L；

3）将增益改变为0.3，幅值为3 L。

给出三组系统仿真相应地输出、控制增益及偏差分别如图3—图5 所示。

图3 r=3 L，γ0=0.1 时系统输出情况

由图3—图5 可知，在0~1 s 内实际的输出流量与期望值误差较大，但是在1 s 后，系统通过对自适应律的调节，被控模型能够很好地跟踪参考模型，输出误差e趋近于零，系统达到稳定。对比图3 与图4 可知，增大输入信号幅值，初始绝对误差峰值由1.2 L 升至1.5 L，稳定时间由0.8 s 缩短至0.6 s，说明控制系统初期的精度降低，但是提高了系统响应速度。对比图4 和图5 可知，增大自适应增益初始值，可以同时提高自适应精度和系统响应速度。由三组仿真均可以看出系统具有良好的跟踪能力。

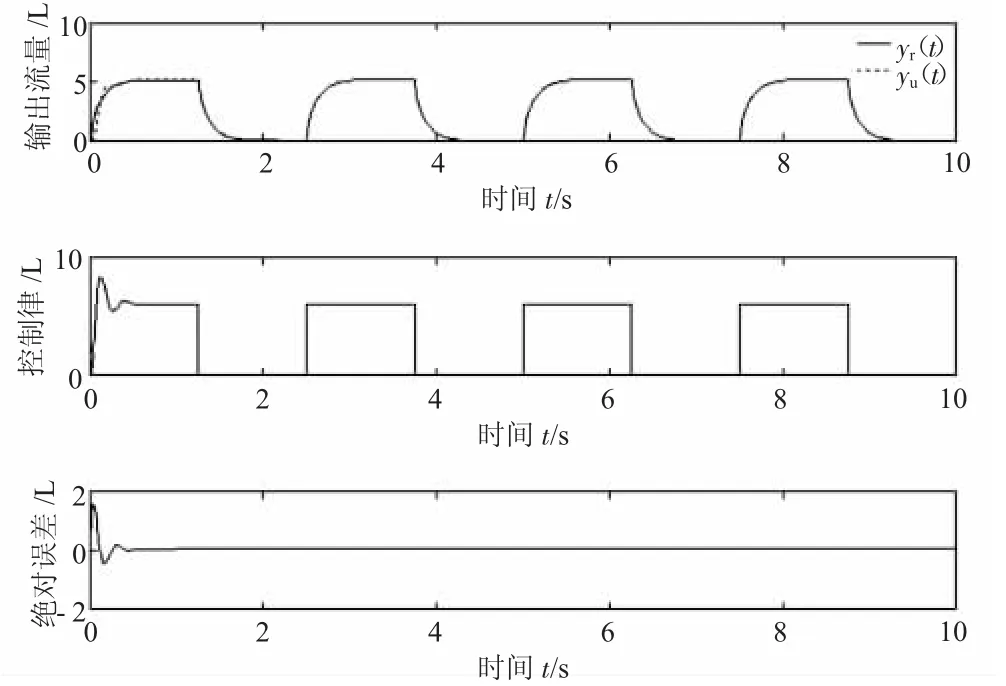
图4 r=6 L，γ0=0.1 时系统输出情况

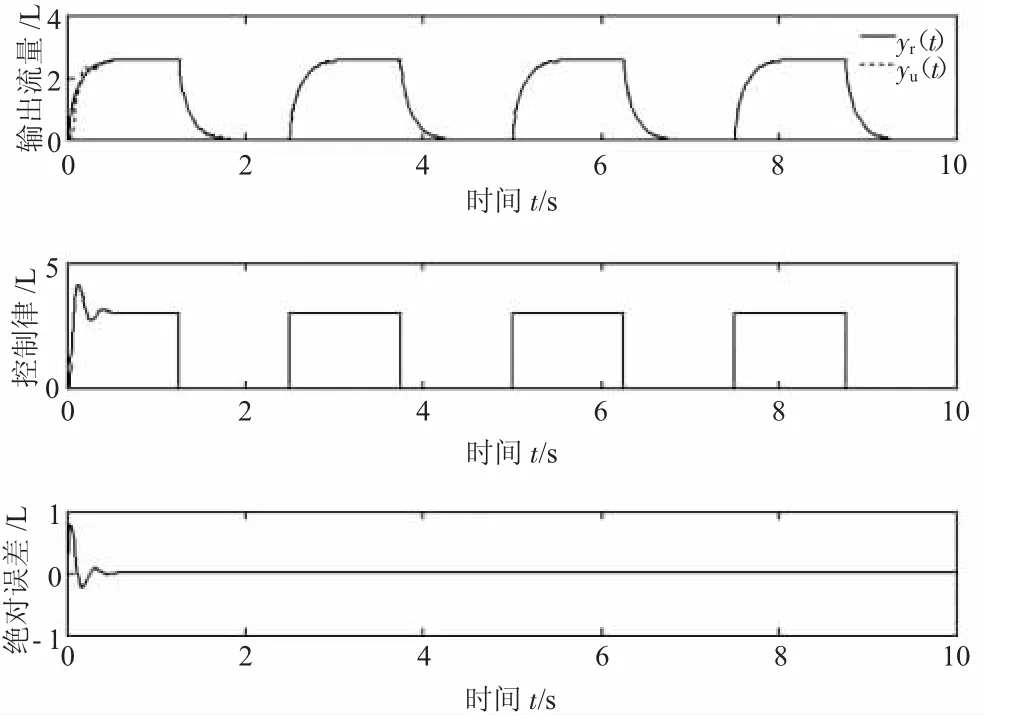
图5 r=3 L，γ0=0.3 时系统输出情况

4 系统整体实验验证

由前节可知，Lyapunov-MRAC 算法可以很好地实现对油路柱塞泵理想模型的跟踪，为验证基于Lyapunov-MRAC 算法的矿用乳化油配液方法的有效性以及优越性，将Lyapunov-MRAC 算法应用于基于PLC 的矿井配液系统中，并且同时与传统PID 乳化液配液方法进行对比。实验中，乳化液配液系统采用西门子S7-1200 作为控制器，设置传统PID 比例、积分以及微分参数分别为1.5、0.5 以及239，具体控制系统结构如图6 所示，给出具体实验结果如图7 所示。

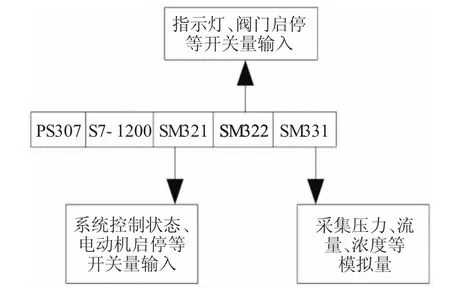
图6 乳化液配比智能控制系统结构图

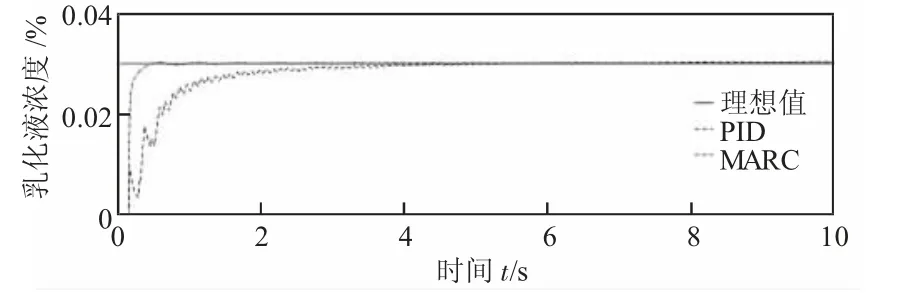
图7 乳化液配液系统浓度输出曲线

根据图7 可知配液系统利用传统的PID 控制算法，系统大约在4 s 时才达到稳态，在达到稳定之前十分不平滑，整定效果欠佳。PID 控制适合线性系统，在实际井下配液过程中往往具有非线性、时变不确定，这种常规的PID 控制器不能达到理想的控制效果，对运行工况的适应能力较差。Lyapunov-MRAC 控制结果大约在1 s 处就实现了稳定，并且一直稳定在浓度设定值。因此对柱塞泵流量进行Lyapunov-MRAC 算法控制，能够使乳化液配液系统中乳化液的浓度快速、准确的响应。

矿用乳化液配液浓度检测值与标准值的最大误差满足煤矿生产要求。提出的算法适用于实际工程应用，提高了乳化液配液的效率，保证了乳化液配液的质量，促进了矿业乳化液配液的速度与自动化程度的提升。

5 结论

针对矿用智能乳化液配液系统展开研究，在详述智能乳化液自动配液系统原理的基础上，提出了符合该类系统的Lyapunov-MRAC 自适应控制策略，并以此为出发点展开了如下工作：

1）采用乳化油密度与温度自适应的增益补足，使乳化油密度可以根据作业中实际温度而调整，减轻了温度对乳化液浓度结果的影响。

2）在阐述Lyapunov-MRAC 自适应控制理论的基础上，深入分析了增益自适应控制算法，给出了自适应控制算法的总体结构图，并利用MATLAB/Simulink进行了控制器模型的设计。

3）采用Lyapunov-MRAC 自适应控制算法对柱塞泵流量控制的二阶非线性系统进行补偿，通过最终的仿真与实验分析得出了油路柱塞泵通过Lyapunov-MRAC自适应控制算法在配液系统的加快调稳等方面明显优于PID 控制的结论，为实现对时变、非线性系统进行准确快速稳定的控制提供了很好的解决。