对“弹簧测力计对拉实验”的思考

黄德斌

中山市第二中学，广东 中山 528400

用“两个弹簧测力计相互对拉实验”来探究一对作用力与反作用力的大小关系，是多个版本高中物理教材在“牛顿第三定律”一节课中引入的一个探究实验。对于这个实验的操作过程和问题讨论，不同版本教材的处理稍有不同，如表1所示。

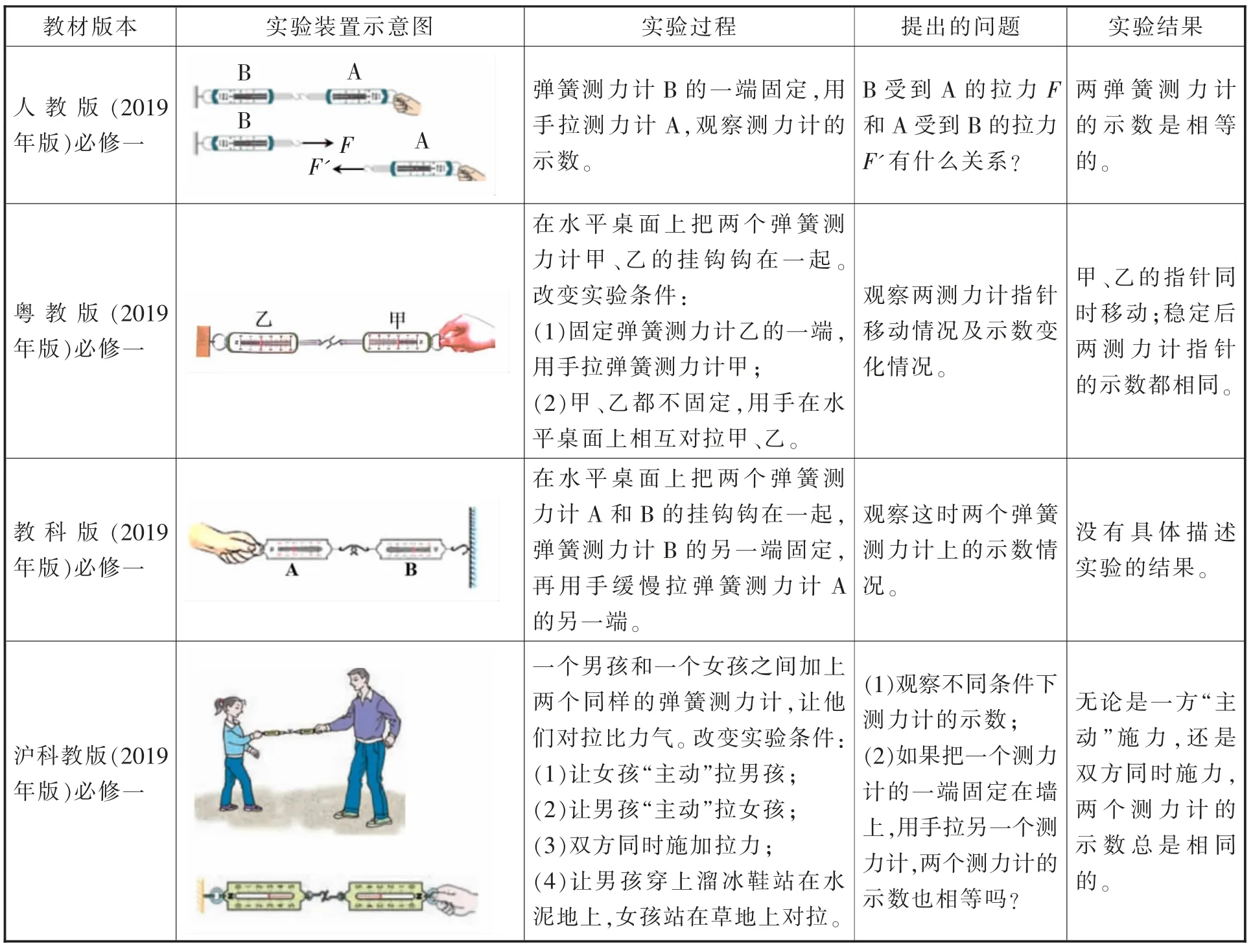
表1 不同版本教材的“弹簧测力计对拉实验”内容

从表1 可以看出，无论是怎样的实验操作过程，实验的目的都是通过这个实验来探究作用力与反作用力的大小关系，并利用“两弹簧测力计的示数相等”这个结果来说明作用力与反作用力的大小是相等的。在表1 所述的实验过程中，两个弹簧测力计的示数相等，真的能说明作用力与反作用力的大小总是相等的吗？ 对这个问题，笔者进行以下讨论。

1 “弹簧测力计对拉实验”的分析

表1 所列出的不同实验过程涉及两弹簧测力计在不同运动状态下的对拉实验，概括起来有三种情况，分析如下。

1.1 平衡状态下的“弹簧测力计对拉实验”分析

粤教版教材对实验结果的描述强调“稳定后两测力计指针的示数是相等的”。稳定后，弹簧测力计处于平衡状态，为了讨论方便，将两弹簧测力计简化为两根水平连接的弹簧，如图1 所示。

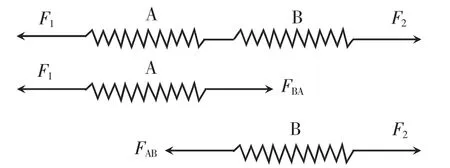
图1 平衡状态下的弹簧测力计对拉实验原理图

在两根弹簧都静止的情况下，讨论图1 中各个力的大小：由平衡条件，把弹簧A，B 看成整体，有F1＝F2；对弹簧A，一端受到弹簧B 对其的拉力FBA，另一端受到拉力F1，大小关系为FBA＝F1；对弹簧B，一端受到弹簧A 对其的拉力FAB，另一端受到拉力F2，大小关系为FAB＝F2。由此可以推理得出FAB＝FBA，可见，此时两弹簧的弹力大小是相等的。所以，在平衡状态下，两个对拉的弹簧测力计稳定后的示数一定是相等的，FAB与FBA是一对作用力与反作用力。

1.2 一起做变速运动状态下“弹簧测力计对拉实验”的分析

若对拉的两个弹簧测力计一起做变速运动，简化的原理图如图2 所示，A，B 为两根相同的弹簧，设其质量均为m，在外力F1，F2的共同作用下，加速度均为a。

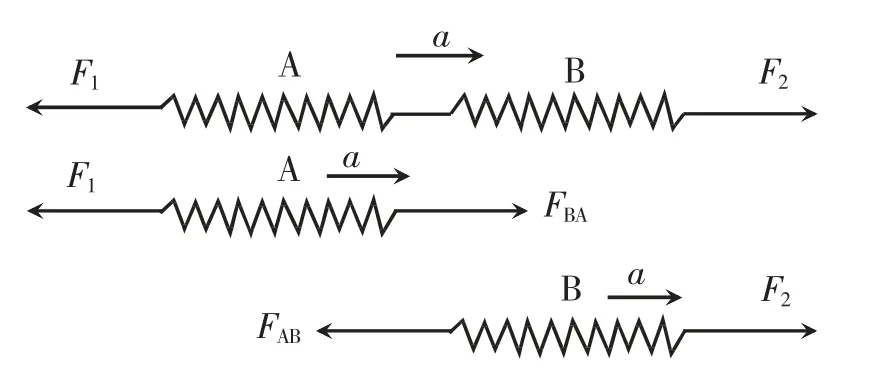
图2 一起做变速运动的弹簧测力计对拉实验原理图

由牛顿第二定律计算各个力的大小：对弹簧A，B 整体，有F2－F1＝2ma；对弹簧A，有FBA－F1＝ma；对弹簧B，有F2－FAB＝ma。由此可以推理得出，可见，在两弹簧一起运动的情况下，两个弹簧测力计的示数也应该是相等的。

1.3 两弹簧测力计不同加速度状态下的“弹簧测力计对拉实验”分析

若两个对拉的弹簧测力计具有不同的加速度，简化的原理图如图3 所示。A，B 为两根相同的弹簧，设其质量均为m，在外力F1，F2的作用下，A 的加速度大小为a1，方向向左，B 的加速度大小为a2，方向向右。

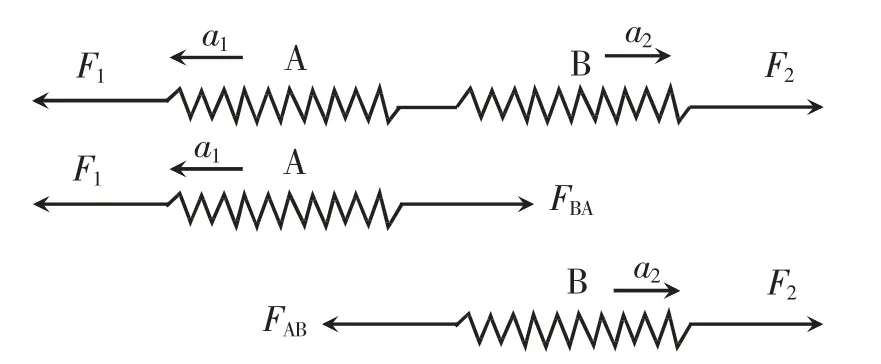
图3 不同加速度状态下的弹簧测力计对拉实验原理图

实际中，由于弹簧测力计挂钩连接处不可伸长，当两弹簧分别向不同方向运动时，弹簧的长度会一直处于变化当中，其示数不稳定，难以测量和讨论其大小的瞬时对应关系。为此，我们假设图3 中弹簧连接处的长度可以变化，两弹簧运动过程中，其加速度大小不变，两弹簧测力计的示数恒定，在这个条件下讨论图3 中各个力的大小：以水平向右为正方向，由牛顿第二定律得，对弹簧A，B 整体，有F2－F1＝－ma1＋ma2；对弹簧A，有FBA－F1＝－ma1；对弹簧B，有F2－FAB＝ma2。由此仍可推理得出FBA=FAB，可见，两弹簧加速度不相等的情况下，对拉的两个弹簧测力计的弹力大小也是相等的。

综上所述，无论弹簧测力计处于平衡状态还是非平衡状态，从理论上分析，对拉的两弹簧测力计示数都是相等的。究其原因，是上述推理过程均用了整体法，把两个弹簧测力计看作整体后，两个弹簧测力计之间的相互作用力属于系统的内力，而用牛顿第二定律的整体法分析系统的运动时，强调的是ΣFi=Σmiai（ΣFi为系统所受外力的矢量和），那么，是不是应用牛顿第二定律的整体法时，本身就默认了系统相互作用的内力是大小相等、方向相反的，所以才都得到了FBA=FAB的结论？ 如果是这样，是不是先有作用力与反作用力总是大小相等、方向相反这个基础，才有整体法应用牛顿第二定律时的ΣFi=Σmiai呢？

其实，牛顿运动定律是在引入力的概念后，动量守恒定律的推理［1］。牛顿的《自然哲学之数学原理》（以下简称《原理》）一书中，对牛顿第二定律的描述为“运动的变化正比于外力，变化的方向沿外力作用的直线方向”［2］。“运动的量”是现代意义的“动量”，力的大小为应用牛顿第二定律分析系统的力与运动关系时，不需要分析系统内力，其根本原因是系统内部的相互作用不会改变系统的总动量，外力的矢量和等于系统内各个物体的动量对时间的变化率，对多个物体组成的系统，有，所以才有ΣFi=Σmiai。

2 对牛顿第三定律实验教学的思考与改进

《原理》中对牛顿第三定律的描述为：“每一个作用都有相等的反作用”，并指出：“作用造成的物体运动的量的变化是大小相等、方向相反的”，“运动的量是运动的度量，可由速度和物质的量共同求出”［2］。可以看到，牛顿第三定律强调的是“在物体间存在相互作用时，作用造成物体的运动变化是相等的”。“运动的变化”即物体“动量的变化”。对于高一的学生来说，显然是在没有学习过“动量”这个概念的前提下学习牛顿运动定律的，但通过对牛顿第一定律和牛顿第二定律的学习，学生对“力与运动的关系”的认识是清楚的。

2.1 探究相互作用力关系的实验设计思路

牛顿第三定律探究实验的教学，可以在学生学习了牛顿第一定律、牛顿第二定律的基础上，沿着“力与运动的关系”这条主线进行教学设计，思路如图4 所示。

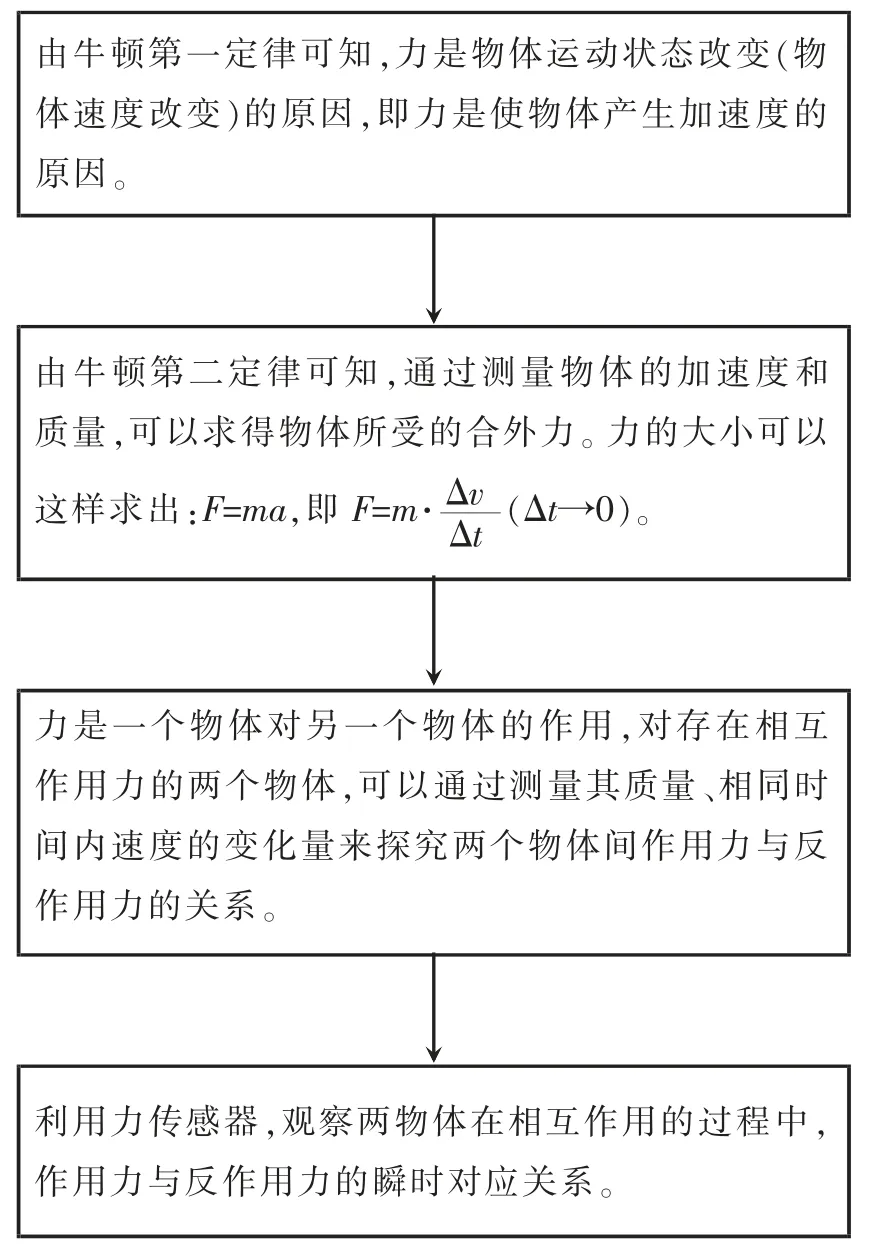
图4 牛顿第三定律探究实验的设计思路

2.2 探究作用力与反作用力大小关系的实验方案及分析

按图4 的思路，设计的实验方案如下。

实验一：探究两滑块在水平气垫导轨上碰撞的过程中，相互作用力的关系。

实验仪器：两个滑块（含挡光片）、光电计时器、气垫导轨、刻度尺等。

实验原理：两滑块在水平气垫导轨上发生碰撞的过程中，在水平方向上，两滑块之间仅存在相互作用的力，如滑块1 受到滑块2 的作用力，速度发生了改变。因此，可以通过测量两滑块的质量及碰撞过程中速度的变化量，代入来探究滑块之间的相互作用力的大小关系。

实验步骤：

（1）在两滑块上安装挡光片、滑块前端安装弹簧片，测量两滑块的质量和挡光片的宽度。如图5 所示，滑块1 的质量m1＝0.223 kg，滑块2 的质量m2＝0.275 kg，挡光片的宽度为0.03 m（计时器设置为从图5 所示的挡光片第一次挡光开始计时，再次挡光停止计时）。

图5 滑块的质量和挡光片的宽度

（2）按图6 所示安装实验装置后，调节气垫导轨水平。

图6 探究两滑块在气垫导轨碰撞过程实验装置

（3）接通光电计时装置，将两滑块分别置于气垫导轨两端，气垫导轨正常工作后，同时轻推两个滑块，两滑块分别经过两个光电门后发生碰撞，碰撞后两滑块弹开，速度均反向，再次分别经过两光电门，计时器记录滑块上的挡光片经过光电门时的挡光时间。

（4）重复步骤（3），得到多组数据。

实验结果：某次测量得到的一组数据如表2所示。

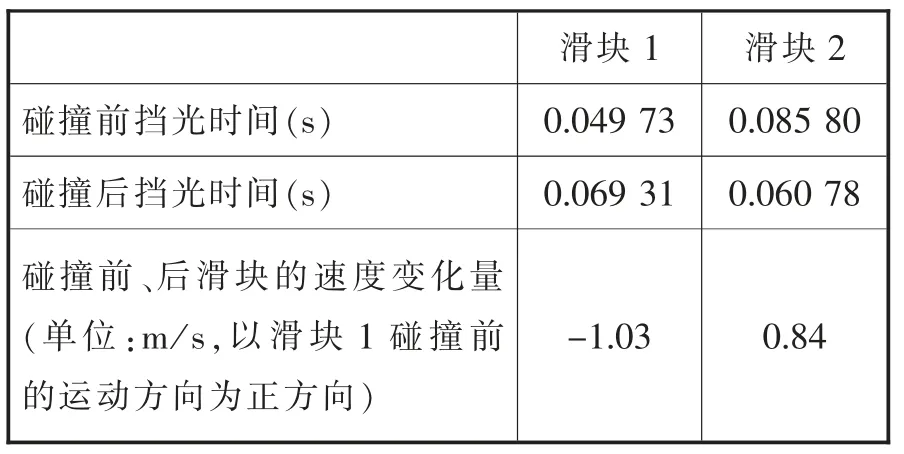
表2 两滑块在气垫导轨碰撞前、后的实验数据

碰撞前后，滑块1 和滑块2 的质量与速度变化乘积分别为m1·Δv1=-0.230 kg·m/s，m2·Δv2=0.231 kg·m/s，对两个滑块来说，碰撞过程相互作用的时间是相等且极短的，设为Δt（Δt→0），由此可以得到，即由于Δt→0，可以认为，在两滑块发生碰撞相互作用过程中，两滑块之间的相互作用力大小是相等的。利用该实验装置还可以设计不同的实验情境（如不同的碰撞类型）进行探究，限于篇幅，本文只列举以上一个实验方案。

上述实验过程测到的是在极短时间内相互作用力的平均值。利用力传感器，可以进一步观察碰撞过程中作用力与反作用力的瞬时对应关系。

实验二：利用力传感器观察碰撞过程中，物体间作用力与反作用力的瞬时对应关系。

实验装置如图7 所示，实验时，将其中一个力传感器固定，手持另一个力传感器与之多次碰撞。通过数据采集器，可以在计算机上显示碰撞过程中，两个力传感器之间的相互作用力的瞬时对应关系，结果如图8 所示。

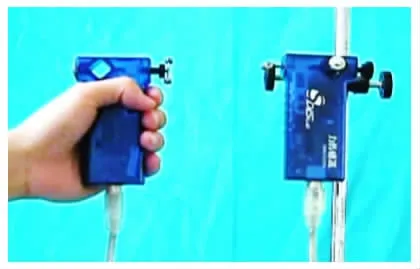
图7 用力传感器探究碰撞过程中的相互作用力关系

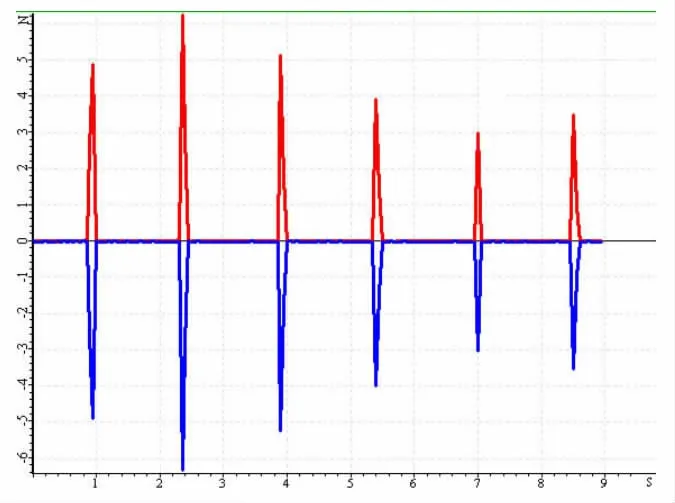
图8 用力传感器探究碰撞过程中的相互作用力关系的结果

3 结语

用滑块在气垫导轨上碰撞来探究相互作用力的大小关系，是在学生没有学习过“动量”的背景下进行的。在教学中可以先不提“动量”这个概念，但实验的教学设计始终沿着“力与运动的关系”这条线索进行，通过分析物体运动的变化来探究其受力的情况。学生经历这样的探究过程后，不会觉得牛顿第三定律就只是讲了“作用力与反作用力大小相等、方向相反”这么简单。这样进行教学设计，可以进一步加深学生对“力与运动关系”的认识的同时，也为今后学习“动量”内容打下良好的基础。另外，将来学生有机会进行更深入的学习，讨论电磁相互作用时，可以认识到“作用力与反作用力大小总是相等”这个结论在有些电磁相互作用的过程中并不成立，需要考虑“场”的动量，描述物理过程更本质的规律是动量守恒定律和能量守恒定律。