基于牛顿迭代法的一类新预估-校正算法

常丑娥，孟国艳

（忻州师范学院数学系,山西忻州 034000）

在科学研究和工程技术领域中，经常将实际问题进行建模，转化为非线性方程f(x)=0 进行处理。其中非线性函f(x)可为高阶多项式或超越函数。在文献[1]中介绍了非线性方程求根公式的演变历史，发现大部分n(n≥5) 次及以上的方程无求根公式可言。在实际问题中，常采用迭代法求解满足精度要求的近似根。在计算过程中若能将迭代收敛速度提高，显而易见，该研究具有重要的现实意义。

文献[2-3]中给出Newton-Raphson method（NR法），简称牛顿法，该方法是一个经典的迭代法，结构简单，收敛速度也较快，至少为二阶收敛。很多学者对其进行改进研究，提出各种改进修正的算法。其中龙爱芳从牛顿迭代公式xk+1=xk-中的导数f'(xk)入手研究，尝试避免计算导数，来减少计算量[4]。WEERAKOON S 等学者从数值积分入手，利用梯形公式近似定积分进行改进，提出算术平均牛顿法（TN 法）[5]。王霞等利用Simpson 公式代替梯形公式，提出Simpson（SN 法）[6]。之后，许多学者利用不同的数值积分给出不同的牛顿迭代格式。陈伟等以先预估后校正的思想提出含双参数的改进型牛顿迭代法[7]。姚梦媛等将牛顿法与数值积分结合，采用高斯公式，提出高斯-勒让德牛顿法（GN 法）[8]。

受牛顿法的启发，结合预估-校正思想，对牛顿法经过变形加速修正处理，提出了一种新的预估-校正算法。

1 理论基础

收敛阶定义[9]设由迭代格式xk+1=φ(xk)产生的迭代序列为{xk}，记误差ek=x*-xk。若∃p,c∈R，且p≥1,c＞0时，有，则称迭代序列{xk}按渐进误差常数c,p阶收敛到x*。当p=1 且0 ＜c＜1 时为线性收敛；当p=2 时，为平方收敛；当p＞1时，为超线性收敛。收敛阶定理[9]设x*=φ(x*)，整数p＞1,φ(p)(x) 在U(x*) 连 续，且φ'(x*)=…=φ(p-1)(x*)=0，而φ(p)(x*)≠0，则由xk+1=φ(xk)产生的序列{xk} 在U(x*)内p阶收敛。

2 新预估-校正算法的构造

由牛顿迭代法

可知，若牛顿法收敛，则迭代收敛阶为二阶，收敛速度较快，每一次迭代后的‖xk-xk-1‖越来越小。因此受启发，再结合双牛顿迭代法[10]，有

此时由（1）、（2）进行了两次循环迭代。对（2）进行移项后，变形可得

由于（6）为隐格式，不易求解，于是进行修正，得到新的迭代算法为

其中：yk为预估步；zk为加速步；xk +1为校正步。

可见，得到的迭代格式（7）为牛顿迭代法的一种新的预估-校正格式，该格式通过加速步起到了加速的作用。

3 理论分析

设f(x)及各阶导数在根x*的U(x*)内连续，初值x0充分接近x*时，有下列结论：

结论1对于f(x)=0，当x*为单根时，有f(x*)=0,f'(x*)≠0，从迭代格式（7）可知，当xk取x*时，=x*，所以f(yk)=f(x*)=0，同理f(zk)=0。

对于迭代格式（7）的迭代函数可取为

结合收敛阶定理可得

由收敛阶定理知，当x*是f(x)=0 的单根时，构造的新算法（7）二阶收敛。

结论2对于f(x)=0，当x*是m(m≥2)重根时，令f(x)=(x-x*)mg(x) 且g(x*)≠0，有f(x*)=f'(x*)=…=f(m-1)(x*)=0，但f(m)(x*)≠0。从迭代格式（7）可知

于是由收敛阶定理知，当x*是f(x)=0 的重根时，构造的新算法（7）线性收敛。

4 数值实验与分析

实验1通过6 个不同的方程[8]来验证新的预估-校正算法的收敛速度，并与GN、SN、TN、NR 法进行比较。程序在同一环境MATLAB R2018a 下编写，设置ε=10-10作为终止条件。这6个方程[8]分别为：

（1）(x-2)3(x+2)4=0 该方程有多个根，均为重根；

（2）x5-10=0 该方程有单根和多重根；

（3）(x-1)6-1=0 该方程有多个根，仅有一个根为重根；

（4）(x-1)e-x=0 该方程有单根（涉及指数函数）；

（5）sin(x-1) +x-1=0 该方程有单根（涉及三角函数）；

（6）x2-ex-3x+2=0 该方程有多个根，均为单根；

由于方程的根的情况各异，所以测试方程具有代表性。测试结果见表1。

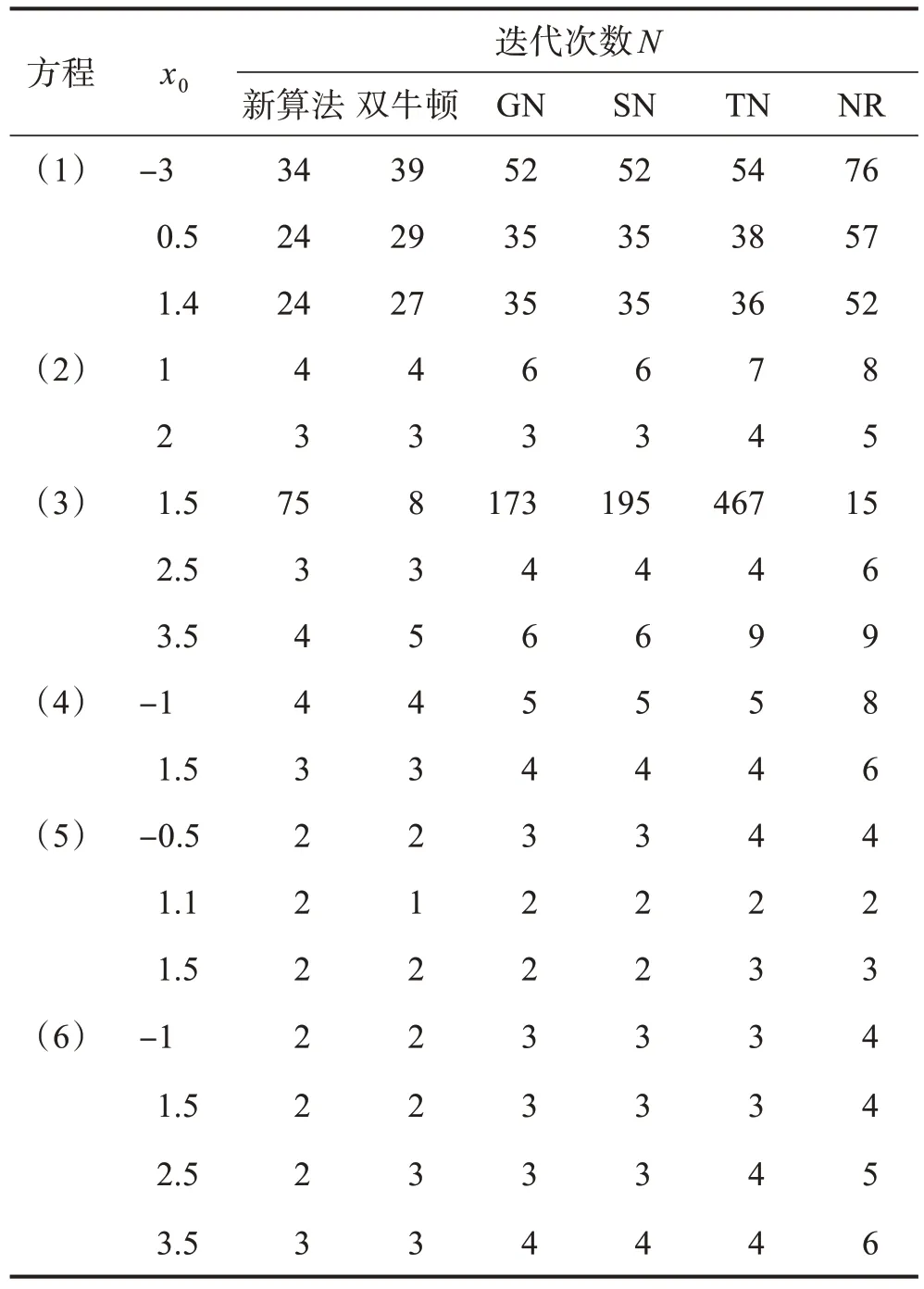
表1 不同方程求根时迭代格式所需的迭代次数

通过数值计算发现，对于同一方程，在不同的初始条件和相同的终止条件下，新算法的迭代次数较双牛顿、GN、SN、TN、NR 的迭代次数少，收敛速度快。当初始值选取较好时，新算法的迭代次数略比其他算法的迭代次数少；当初始值选取的不是较好时，新算法的迭代次数明显比其他算法的迭代次数少。

实验2通过3 个不同的方程[9]来验证新的预估-校正算法的收敛速度，并与双牛顿、GN、SN、TN、NR法进行比较。程序同样在MATLAB R2018a 下编写，设置ε=10-10作为终止条件。这3个方程[9]分别为：

测试结果见表2。

表2 不同方程求根时迭代格式所需的迭代次数

通过高次代数多项式方程和超越方程的计算，结果表明：对于同一方程，在不同的初始条件和相同的终止条件下，新算法的迭代次数比双牛顿、GN、SN、TN、NR 的迭代次数少，至多相等，可见新算法在收敛速度上占优势。

从表2 可看出，当初始值选取较好时，新算法的收敛速度从迭代次数上分析略占优势；当初始值选取的不是较好时，新算法的收敛速度明显比其他算法快。

5 结束语

基于双牛顿迭代法，结合预估校正思想，构造出的新的预估-校正迭代格式，结构紧凑，收敛阶至少为二阶收敛，计算过程相对有些复杂，效率指数也不是很高，但迭代次数较少，能起到提高收敛速度的效果。通过不同的算例分析可知，对于同一方程在同一终止条件下，当初始值不同时，迭代次数不同。经过与其他几种迭代法比较，发现该迭代法的收敛速度快，迭代次数少，具有一定的可行性和应用性。