基于约束的多维Apriori 改进算法

王志昊，苏明月，李东方，沈炜，杨光

（北京计算机技术及应用研究所，北京 100854）

0 引言

现代社会，生产力快速发展，通过不断变革生产信息技术，人们大大提高了创造和收集数据的能力，迅速扩大了数据资料的规模。急剧增长的数据资料和数据库迫使人们采用新的技术手段和工具来处理海量的数据，自动自主地帮助人们管理、提取并分析有用的信息，来发掘有价值的知识，为人们提供决策服务。由此，数据挖掘（Data Mining）[1]在这样的宏观背景下诞生。将数据挖掘技术充分运用到现实的生产中，提高企业生产的效率，降低生产成本。数据挖掘的应用范围较广，如聚类、预测、分类、异常分析以及相互关联性分析。

数据挖掘中，关联规则是较为主要的研究对象。其中频繁项集的产生是最核心、最受关注的问题。关联规则反映了一个事物与其他事物之间的相互依存和关联性[2]。换句话说，关联规则是一种隐含在数据中的知识模型，其通过量化数字，从海量数据中挖掘出有价值的数据项之间的相关关系[3]。

关联规则挖掘最初由Agrawal[4]等人于1993 年提出，通过关联规则的挖掘可以找出潜藏在数据库中各个属性之间的关系，辅助人们更合理地进行商业活动、金融决策和生产生活等。

目前，典型的挖掘关联规则的算法主要是Apriori 算法[5]，其核心在于找到数据库中的所有频繁项集。Apriori 算法通过逐级产生频繁项集并利用先验性质缩减候选项集产生。在扫描数据集的过程中，Hossain 提出可使用自动递归连接来挖掘候选项目集[6]，然后剪枝用于挖掘频繁项集。2021年，Li 等人提出基于时序约束的关联规则挖掘，减小了系统开销[7]。Wang 等人利用MapReduce 的思想改进Apriori 算法，有效提高了搜索效率[8]。2022年，Dhinakaran 等人集成Apriori 算法和仿 生算法，通过降低处理大型数据集时的低运行时性能来解决频繁项集问题[9]。

现有的Apriori 算法主要适用于单维布尔型数据的关联规则挖掘，若想挖掘多维关联规则，需将多维事务集的数据属性进行拆分、映射，转化成单维布尔类型事务集，再利用Apriori 等算法进行挖掘，但当多维数据维度较高或属性取值较多时，挖掘过程将会产生过多的候选项集，严重影响算法执行效率。针对该问题，目前多是通过改进典型Apriori 算法[10]、将多维事务集映射到新结构上进行挖掘[11]、结合智能算法[12]等方式进行多维关联规则的挖掘。然而这些方法大多仅仅通过支持度等客观条件控制挖掘过程，导致挖掘结果缺乏针对性，存在大量用户不感兴趣的冗余规则。并且由于Apriori 算法中候选项集数量与最长频繁项集的长度成指数关系，因此当事务集包含项目数量过多时，算法将会面临候选项集搜索空间爆炸的问题。

因此，针对以上不足，本文在前人研究的基础上，以提高算法处理效率、深入挖掘数据间关联规则为优化目标，将用户约束引入挖掘过程，提出基于约束的多维Apriori 改进算法（Algorithm of Multi-Dimensional Apriori with Constraints，MDAC），在进行多维关联规则挖掘的同时，降低了扫描数据库的开销，提高了检索效率，实验证明MDAC 优于传统的多维Apriori 算法。

1 关联规则挖掘

关联规则挖掘是进行大数据分析最常用的研究方法之一，它的目的在于从庞大数据集中找出各项之间的关联，而这种关联不会在数据中表现出来，需要进行关联分析，分析多个变量之间的联系。关联规则挖掘中最重要的两个参数是支持度、置信度，参数取值会直接影响最后得到的关联结果。

（1）关联规则

关联规则主要表示形式为A⇒B，A称为规则前项，B称为规则后项，符号⇒称为关联，A称为⇒的先决条件，B则称为⇒的结果。其中A≠Ø、B≠Ø且A∩B=Ø，在自然语言中，可以将其理解为“如果A，那么B”，该规则说明了A与B之间存在着某种关联关系。

（2）支持度

支持度是用来衡量关联规则重要性的关键量，支持度越高关联规则越重要。假设D为事务集，关联规则A⇒B在事务集D中成立，支持度s即包含A∪B的事务（即事务包含项集A和B中所有项）在D中的百分比，表示为P(A∪B)。支持度的计算公式如下所示：

（3）置信度

置信度是用来衡量关联规则可靠性的关键参数，置信度的高低代表关联规则可信程度的高低。关联规则A⇒B在事务集D中具有置信度c，其中c是D中事务在包含项集A的条件下也包含项集B的概率，表示为条件概率P(B|A)。置信度的计算公式如下所示：

（4）强关联规则

假设D为事务集，A、B为项集，若存在规则A⇒B的支持度s和置信度c分别不小于预先设定的最小支持度阈值（min_sup）和最小置信度阈值（min_conf），则称规则A⇒B为强关联规则。根据式（1）和式（2），可以得出由支持度计算置信度的公式：

式（3）表明规则A⇒B的置信度可从A和A∪B的支持度计数推出，即一旦得到A、B和A∪B的支持度计数，则可导出对应的关联规则A⇒B和B⇒A，并且可以直观判断它们是否为强关联规则。

（5）多维关联规则

关联规则根据规则所涉及的谓词数，可以分为单维关联规则和多维关联规则两类。若关联规则的前项和后项包含两个或更多的谓词，则为多维关联规则。多维关联规则由于涉及多个谓词，每个谓词各自包含自身的项目集合，因此挖掘过程需要从多维事务集中搜索频繁谓词集。

典型的多维Apriori 算法采用的方法是在连接频繁集生成候选集时，提前判断连接之后的结果中是否存在重复的维度属性，若不重复则进行连接并根据Apriori 性质完成剪枝，重复则取消本次连接。这是由于存在重复维度的候选集在事务集中并不存在，删减此类候选集，可有效避免后续无意义的数据库扫描计数操作所导致的算法开销，提高了多维关联规则的挖掘效率。除此之外，研究人员关于多维关联规则挖掘算法还进行了其他改进方向的研究[10-14]，主要研究成果包括通过将多维事务集映射到新结构上进行挖掘、结合智能算法等算法改进思路，各类算法对比情况如表1 所示。

由表1 可知，多维Apriori 算法更具有普适性，但因挖掘过程中产生过多候选谓词集导致扫描数据库次数较多，影响算法执行效率，这促使本文提出MDAC 算法，通过用户约束条件限制候选谓词集的产生，减少数据库扫描次数，同时能够保证挖掘结果更符合用户的兴趣度，减少冗余规则生成。

2 基于约束的多维Apriori 改进算法

Apriori 算法主要分为两步：第一步是找到数据库中满足最小置信度阈值的项目集；第二步是找出所有支持度大于阈值的项目集，并找出置信度大于阈值的强关联规则。传统多维Apriori 算法的挖掘过程仅仅采用支持度和置信度等客观条件进行控制，缺乏用户的主动参与，导致挖掘结果缺乏针对性。通过将约束引入挖掘过程，可以通过用户兴趣控制挖掘流程，进而减少部分候选谓词集的产生，一方面提高了算法执行效率，另一方面也保证最终生成用户感兴趣的关联规则。

现有的基于约束的关联规则挖掘算法主要包括了MultipleJoins、Reorder、Direct 以及Separate 等算法[15-17]，其中Separate 算法直接生成满足项约束的频繁项集，在此基础上逐层迭代得到全部频繁项集，相比于其他算法在生成的候选集数量上更有优势。本文主要借鉴了Separate 算法的思想，针对多维Apriori 算法进行改进。

2.1 相关定义

假设D={d1,d2,…,dn}是多维事务集所有维度的集合，其中维度dk的属性取值包括{ik1,ik2,…,ikm}，每一个维度对应规则中的一个谓词。

挖掘算法在上述事务集上搜索频繁谓词集L，若其中包含谓词数为k，则称为频繁k谓词集，记作Lk。

用户可对谓词进行约束，并采用布尔表达式的形式进行表示，如(A∧B) ∨C，该式表明约束条件为“包含谓词A和B或包含谓词C的多维关联规则”。进一步针对谓词的取值进行约束，则如(A=a1) ∧B，表示“包含谓词A和B且谓词A取值为a1的多维关联规则”。

2.2 改进方法

上文提到，经典的 Apriori 算法对数据库进行了多次遍历，为此形成了大量的候选集，给系统 I/O 产生了比较大的负载，对系统内存的调动也有较大的压力。MDAC 通过对数据库进行压缩来改进 Apriori 算法，根据Apriori 性质的定义，频繁谓词集的任意非空子集也必定是频繁的，由此可以推出，若某一谓词集是非频繁的，那么包含该谓词集的任意超集也同样是非频繁的。

因此，为了缩减候选谓词集以达到提高挖掘效率的目的，MDAC 根据用户约束条件，例如针对规则中谓词的约束或是更进一步针对某个谓词取值的约束，确定满足用户约束的频繁谓词集，在此基础上，再将其余未约束维度加入进来，逐层迭代搜索符合约束条件的所有频繁谓词集。依照上述思想，MDAC 扫描数据库次数大大减少，挖掘结果也更具有针对性。

具体来说，首先依据用户约束条件，将多维事务集依照维度进行划分，选取仅包含被约束维度数据的部分事务集，称为约束事务集。之后扫描约束事务集，确定满足用户约束条件和支持度要求的频繁谓词集及其支持度计数。同时记录包含频繁谓词集的事务ID，利用该事务ID 集合（即全部事务ID 集合的一个子集）可对事务集进行删减，将已确定不满足约束条件的事务提前剔除，事务数量的减少可以有效加快后续扫描数据库的速度。然后，以满足约束的频繁谓词集为基础，与其他未约束维度下的频繁1 谓词集进行连接，生成新的频繁谓词集，再不断迭代直到不再产生新的谓词集为止，过程中同样利用Apriori 性质完成剪枝。

相比于多维Apriori 算法，MDAC 通过约束确定了用户感兴趣的频繁谓词集，之后通过连接与剪枝等操作产生的候选谓词集均是该频繁谓词集的超集，MDAC 一方面可以避免无关谓词集的产生，减少数据库扫描次数；另一方面也基于约束尽早地删减了数据集中事务的数量，降低了扫描数据库的开销。最终得到的全体频繁谓词集，既满足最小支持度阈值要求又符合用户约束，可由此生成用户感兴趣的多维关联规则。

2.3 算法描述

在算法运行之前，预先设置最小支持度阈值min_sup 和最小置信度阈值min_conf，以及用户约束条件。根据约束条件，从多维事务集T选取约束事务集Tcstr。具体挖掘过程如下：

（1）扫描Tcstr，得到满足约束的各谓词集及支持度计数，并与min_sup 进行对比，得到频繁谓词集Lcstr，同时记录包含频繁谓词集的事务ID 集合Tid；

（2）根据步骤（1）得到的Tid，对事务集进行删减，仅保留Tid部分，得到删减后的事务集T′；

（3）针对删减后的事务集T′，搜索未约束维度下的频繁1 谓词集F；

（4）连接Lcstr和F，生成候选k谓词集Ck；

（5）根据Ck扫描T′相应维度并计数，得到频繁k谓词集Lk；

（6）由Lk连接生成候选k+1 谓词集Ck+1，连接过程判断是否有重复维度，若重复则取消本次连接，并利用Apriori 性质剪枝；

（7）根据Ck+1扫描T′相应维度并计数，得到频繁k+1谓词集Lk+1；

（8）循环步骤（6）和步骤（7），直到不产生新的候选谓词集，最终得到全部频繁谓词集L；

（9）根据最小置信度阈值min_conf，生成多维关联规则集。

因此，基于约束的多维Apriori 改进算法MDAC 的挖掘过程如图1 所示。

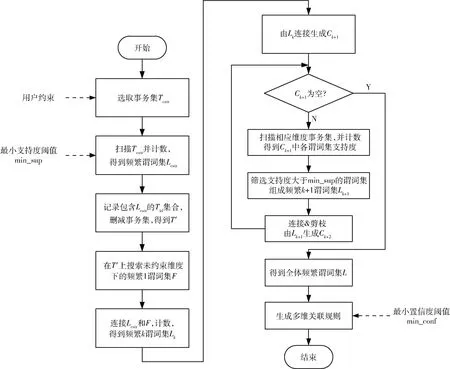
图1 基于约束的多维Apriori 改进算法挖掘流程

上述算法流程中，步骤（6）由频繁k-1 谓词集Lk-1连接生成候选k谓词集Ck的伪代码示意如下：

在最终得到满足用户约束条件的频繁谓词集L后，即可根据最小置信度阈值生成多维关联规则。需要说明的是，此时若用户对于被约束谓词在规则中出现的位置同样提出了要求，那么可以在规则生成过程中限定关联规则的模式，例如要求被约束的谓词出现在规则的右部，形如{A,B,…} ⇒CSTR，那么相应的规则生成伪代码示意如下：

输入：频繁谓词集L、最小置信度阈值 min_conf；

输出：关联规则集R。

3 实验结果分析

实验所用数据来自某第三方FPGA 评测机构，包含多种FPGA 测试工具结果、经测试人员分析确认后的FPGA 代码设计缺陷信息等多个维度数据，实验应用基于约束的多维Apriori 算法，期望发现FPGA 代码缺陷与测试工具结果之间的关联关系。

在进行挖掘之前为了给挖掘算法提供更高质量的数据，需要先对采集到的原始数据进行预处理。首先针对数据采集过程中种种原因导致的数据缺失、数据重复等问题进行数据清理，然后将来自不同数据源的数据进行集成，并检测属性间的相关性，以删减掉冗余属性，最后再将其中的数值型数据离散化，以便于得到更好挖掘效果。

经过数据处理后得到的FPGA 代码缺陷事务数据库共有事务38 942个，包含4 个数据维度。本文采用R 语言进行算法的实现，为了证明MDAC 的性能，本节将MDAC 与未引入约束的多维Apriori 算法进行对比，其余实验设置保持相同，所有实验均进行了10次，实验结果为10 次实验的平均值。

假设用户期望发现与FPGA 代码缺陷数据中缺陷类型维度相关的多维关联规则，约束条件设置为“包含谓词缺陷类型的关联规则”。在不同的最小支持度阈值min_sup 条件下，多维Apriori 算法与引入约束后的改进算法MDAC 在频繁谓词集搜索过程上的时间开销对比如图2 所示。

图2 不同支持度下算法时间开销对比示意图

由图2 中可以看出，随着最小支持度阈值设置的变化，MDAC 算法在搜索频繁谓词集的过程中，通过缩减事务集以及压缩不符合约束的候选谓词集，有效减小了时间开销，相比于多维Apriori 算法，MDAC 平均减少时间开销幅度约为46.85%。并且，由于用户可以通过加强对于关联规则结果的约束，消减更多不满足约束的事务以及候选谓词集，降低扫描数据库带来的开销，进一步提高了算法效率。

除去时间开销降低之外，MDAC 算法在生成频繁谓词集数量方面同样有所变化。假设约束条件同样设置为“缺陷类型”维度，在不同支持度阈值条件下，不考虑频繁1 谓词集（频繁1 谓词集不用于生成多维关联规则），两个算法搜索得到的频繁谓词集数量对比情况如图3 所示。

图3 不同支持度下频繁谓词集生成数量对比示意图

在不同支持度阈值下，基于约束的改进算法MDAC搜索得到的频繁谓词集，相比未引入约束的多维Apriori算法而言，谓词集数量普遍下降，降低幅度约为41.06%。此处以最小支持度阈值设置为16%为例进行进一步对比，多维Apriori 算法挖掘得到的频繁谓词集如表2 所示，而MDAC 算法挖掘出的频繁谓词集如表3所示。

表3 基于约束的改进算法生成频繁谓词集

由表2、表3 可知，通过引入约束减少频繁谓词集数量的同时，用户感兴趣的包含缺陷类型维度属性的频繁谓词集也并没有出现任何错误或者遗漏的情况，相比于多维Apriori 算法产生的频繁谓词集，减少的部分谓词集均不满足用户约束条件，对于用户感兴趣的多维关联规则挖掘结果不会产生影响。

4 结论

本文提出基于约束的多维Apriori 改进算法MDAC，该算法通过将用户约束引入挖掘过程，缩减候选谓词集的产生，提高了算法执行效率，并减少了冗余规则的产生，弥补了原算法缺乏用户主动控制的不足。通过实验对比，证明了该算法相比于传统的多维Apriori 算法，从频繁谓词集的搜索效率以及挖掘结果的准确性方面均获得了改善。