数字化测绘技术在大型水利工程中的应用研究

刘佳城

(深圳市广汇源环境水务有限公司，广东 深圳 518000)

0 引言

常规测绘方法的测量效率不高，且无法保证其测量精度，而数字化测绘在保障测量精度的同时，还可提高测绘效率，近年来，许多专家学者针对数字化测绘开展相关研究。

杜丽雯等人[1]以某水利枢纽为研究对象，基于GPS数字化测绘技术，开展水利枢纽大坝的测绘工作，结果表明，该方法的测量精度较高。张杰等人[2]以某矿山地质工程为研究对象，基于数字化测绘技术，提高其测绘效率，研究结果可为相关工程测绘提供依据。梁标丽[3]基于GPS高程拟合技术，对某建筑工程的测量精度进行分析，结果表明，该技术可显著提高测量精度和效率。陈文坤等人[4]以某水利工程为研究对象，基于数字化技术，对该工程的测绘精度进行分析，结果表明，该技术的测绘精度满足相关规范的要求。魏超[5]分析影响数字化测绘效率的影响因素，结果表明，监测点的布置方式对其测量效率的影响较大。

本研究以某水利枢纽为研究对象，采用GPS数字化测绘技术进行测绘，通过差分处理的方法对该工程的观测结果进行处理，分析GPS数字化测绘技术的测绘精度及应用的可行性。

1 工程概况

本研究以某水利枢纽为研究对象，该水利枢纽是一宗以防洪、供水、灌溉为主，兼顾发电等综合利用的I等大(1)型工程，设计轴线总长为2993.6m，坝址以上集雨面积749km2，总库容4.68亿m3，年城市供水1.94亿m3，灌区干渠总长87.6km，总灌溉面积9.92万亩，年灌溉水量1.3亿m3；年平均发电量3760万kw·h。主要工程建筑物由拦河坝、溢洪道、引水隧洞及发电厂房组成。设置64孔泄水闸，其中，孔口净宽26m的常规泄水闸60孔，孔口净宽60m的大孔泄水闸4孔，闸底板高程分别为0、2、4m。枢纽左岸设置3线单级船闸，船闸级别为I级，闸室有效尺度采用280m×34m×5.5m(长×宽×最小槛上水深)。

2 水利枢纽工程坝型数字化测绘

本研究以某水利枢纽工程为研究对象，采用GPS数字化测绘技术，对该工程进行测绘，并分析GPS数字化测绘技术的测绘精度。通过差分处理的方法对该工程的观测量进行处理，差分观测方程如式(1)所示。

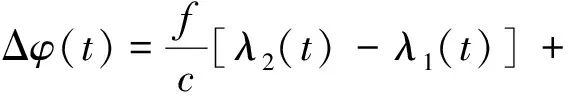
Δ1·IP(t))-(Δ2·T(t)-Δ1·T(t))]

(1)

式中，f—频率，Hz；c—光速，取299792.458km/s；ηti(t)—接收机到观测站的几何距离，km；λi(t)—卫星到观测站的几何距离，km；Δi·IP(t)—卫星信号受到传播距离影响的程度。

3 结果分析

为分析GPS数字化测绘技术的测绘精度，研究该技术在测量基线长度时的误差，星历给出的卫星在空间的位置与实际位置存在一定的差异性，会造成定位的系统误差，所以，还需分析卫星星历误差对该技术测绘精度的影响，其基线长度-误差曲线如图1所示。由图可知，不同星历误差下的基线长度-误差曲线具有一致性，其基线长度与误差间呈正相关关系，随着基线长度的增大，GPS数字化测绘的误差逐渐增大，说明当测绘范围较大时，采用GPS数字化测绘技术得出的测量误差较大，为保证该技术侧测量精度，应尽量缩小其测绘范围。对比不同星历误差下的测绘误差可得，在同一基线长度下，星历误差与测绘误差间呈正相关关系，说明星历误差对GPS数字化测绘技术的测绘精度存在显著的影响；且当基线长度较小时，不同星历误差下的测绘误差差值较小，随着基线长度的增大，不同星历误差下的测绘误差逐渐增大，说明当测绘范围较大时，星历误差的变化对GPS数字化测绘误差的影响较大，在实际工程中，当测绘范围较大时，采用GPS数字化测绘技术得出的测绘结果误差较大，为提高测绘精度，可降低星历误差来提高测绘的准确性。

图1 基线长度-误差曲线

灵敏度椭圆半径可用于表征测绘结果的灵敏性，当其值越大时，表明测绘结果的灵敏性较差；而基线可用于精确测量长度，为分析基线数量对GPS数字化测绘灵敏度的影响，分析不同基线数量下，灵敏度椭圆半径的变化规律，其GPS控制网点-灵敏度椭圆半径曲线如图2所示。由图可知，在同一基线数量下，不同GPS控制网点的灵敏度存在一定的差异性，说明测绘地段会影响测绘的灵敏度。对比不同基线数量下的灵敏度椭圆半径可得，在同一GPS控制点下，基线数量与灵敏度椭圆半径呈负相关关系，当基线数量为10条时，GPS数字化测绘的灵敏度椭圆半径最大，当基线数量为30条时，GPS数字化测绘的灵敏度椭圆半径最小，说明基线数量对于GPS数字化测绘的灵敏度存在显著影响；且当基线数量较大时，不同基线数量下的灵敏度差值较大，增大基线数量可提高GPS数字化测绘过程的灵敏度及测绘可靠性，在实际工程中，选取合适的基线数量有利于提高GPS数字化测绘的测绘效果。

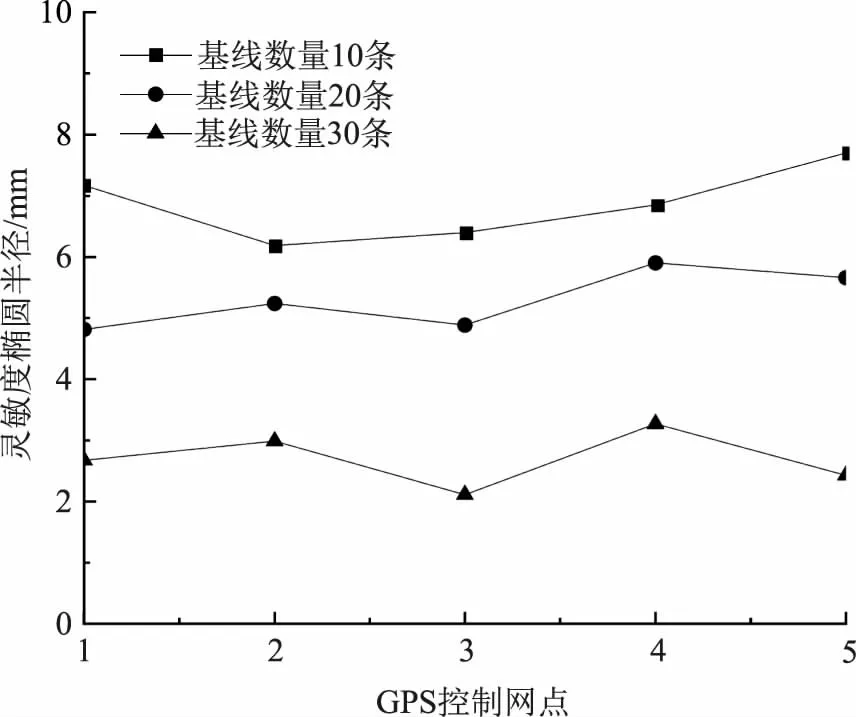
图2 GPS控制网点-灵敏度椭圆半径曲线

通过差分处理对GPS数字化测绘数据进行处理可提高其测绘精度，为分析差分处理对测绘精度的提升效果，以30条基线数量的GPS数字化测绘数据为研究对象，分析不同差分处理次数后的测量误差，其x方向的监测点序号-测量误差曲线如图3所示。由图可知，不同监测点的测量误差具有一定的差异性，其中，当进行1次差分处理后，监测点5的测量误差最大，其值为35.2mm；监测点1的测量误差最小，其值为31.7mm，不同监测点间的误差差距较小，说明采用GPS数字化测绘得出的测绘结果精度较为稳定。对比不同差分处理次数下的测量精度可得，当进行3次差分处理后，采用GPS数字化测绘得出的测量误差最小，其平均测量误差小于10mm；进行1次差分处理的测量误差最大，其平均误差为33.6mm，说明通过差分处理对GPS数字化测绘数据进行处理可提高其测绘精度，且差分处理次数越多，其测绘精度越高。

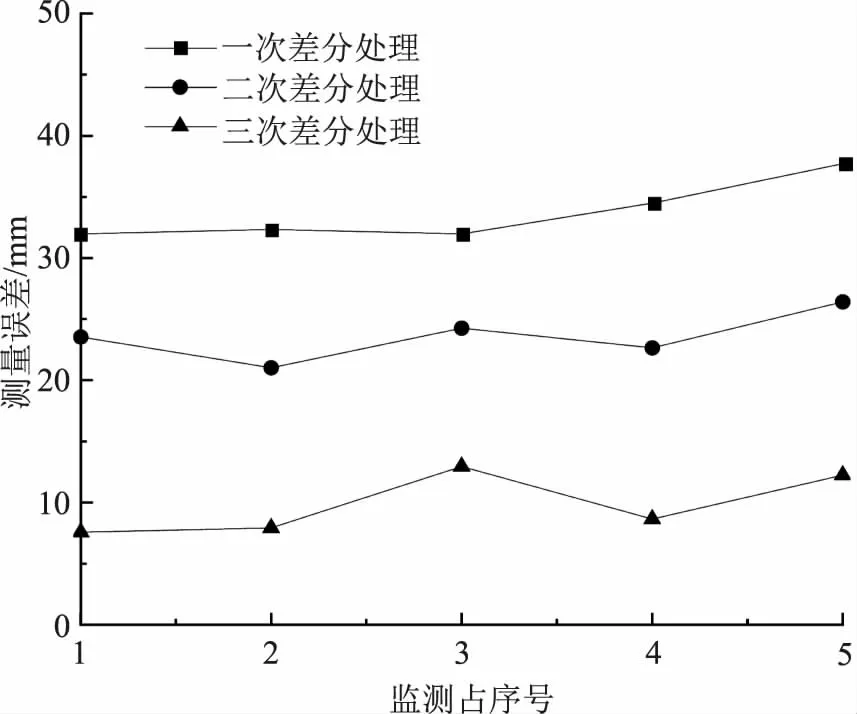
图3 x方向的监测点序号-测量误差曲线

其y方向的监测点序号-测量误差曲线如图4所示。由图可知，当进行1次差分处理后，监测点5的测量误差最大，其值为41.1mm；监测点2的测量误差最小，其值为30.2mm。对比不同差分处理次数下的测量精度可得，差分处理次数与GPS数字化测绘精度呈正相关关系，当差分处理次数较大时，采用GPS数字化测绘得出的精度较高，当进行3次差分处理时，个监测点的测量误差均小于10mm。说明对GPS数字化测绘数据进行差分处理可提高其测绘精度，且差分处理次数越多，其测绘精度越高。

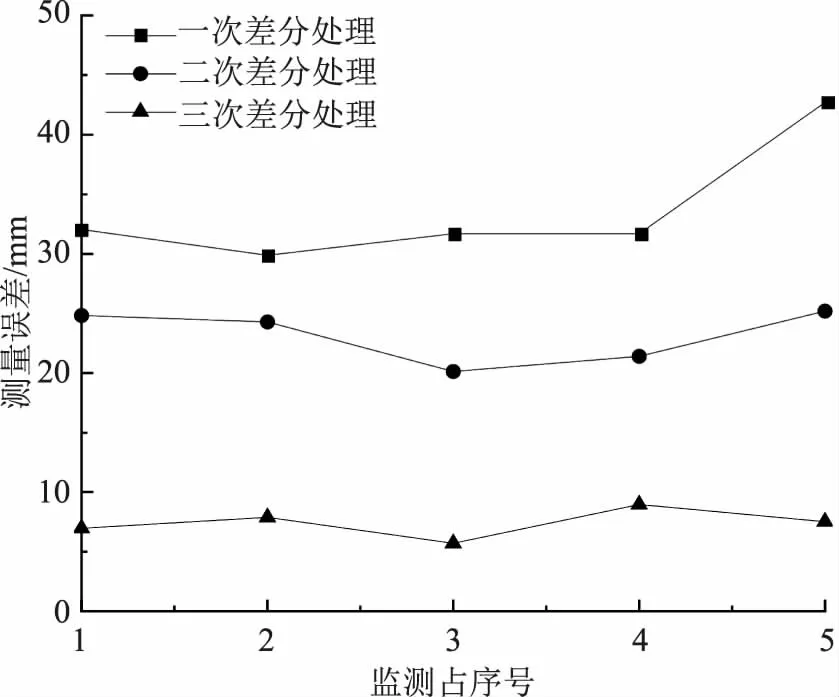
图4 y方向的监测点序号-测量误差曲线

其z方向的监测点序号-测量误差曲线如图5所示。由图可知，z方向的平均测量误差大于x方向、y方向的平均测量误差，说明采用GPS数字化测绘技术对于平面测绘的精度较高，对于高程等竖向测量的精度较差。对比不同差分处理次数下的测量精度可得，当差分处理次数较大时，采用GPS数字化测绘得出的精度较高，当差分处理次数较小时，采用GPS数字化测绘得出的精度较低，说明对GPS数字化测绘数据进行多次差分处理，有利于提升其测量精度。综合以上分析可得，差分处理对于x、y、z方向GPS数字化测绘的测量精度均有显著的提升效果，且差分处理次数越多，其测绘精度越高；因此，可采用差分处理的方式提高测绘精度[6]。

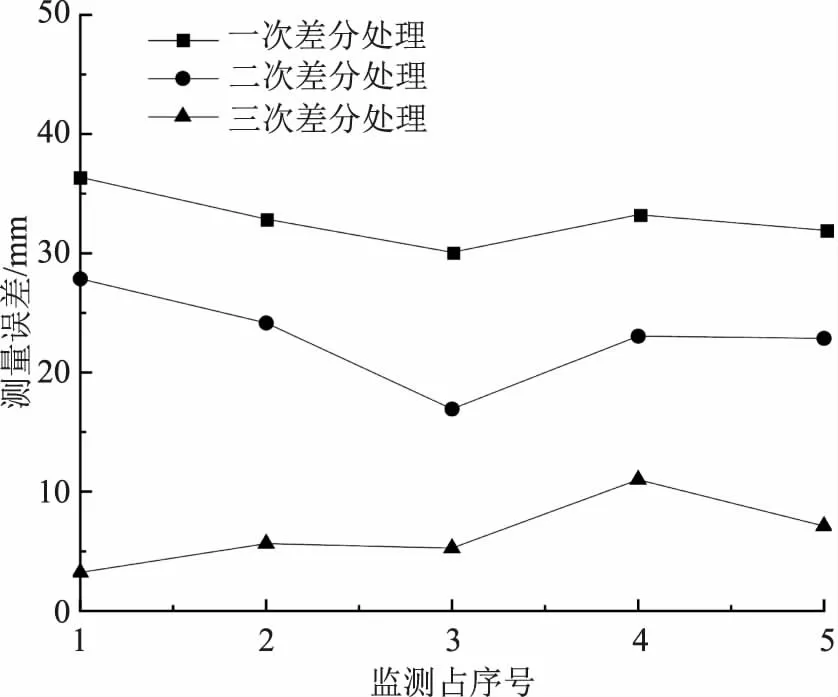
图5 z方向的监测点序号-测量误差曲线

4 结论

本文以某水利枢纽为研究对象，采用GPS数字化技术进行测绘，对观测结果进行差分处理，分析测绘精度，得出以下结论。

(1)不同星历误差下的基线长度-误差曲线具有一致性，基线长度与误差间呈正相关关系，随着基线长度的增大，GPS数字化测绘的误差逐渐增大，为保证该技术测量精度，应尽量缩小其测绘范围。

(2)不同监测点间的误差差距较小，采用GPS数字化测绘得出的测绘结果精度较为稳定。对测绘数据进行差分处理可提高其测绘精度，差分处理次数越多，测绘精度越高。