基于模糊控制的智慧城市路口交通灯配时优化方法

李 斌，傅正阳，郑江萍

（杭州市公安局交通警察支队西湖大队，浙江 杭州 310000）

0 引言

近年来，随着智慧城市的不断发展，城市交通面临的压力逐渐增大，特别是在路况复杂的交通路口，容易因为交通灯配时标准不合理而出现拥堵现象。针对该问题，陈海洋等[1]引入克隆选择算法，对克隆抑制算子与种群刷新算子进行改进，将交通灯状态设置问题转换成克隆选择算法搜索最优解问题，实现智慧城市路口交通灯配时优化,但该方法在实际应用中优化效果不佳，路口仍出现拥堵问题。陈小红等[2]研究了不确定交通需求下的交叉口信号配时区间优化模型，通过构建信号配时参数区间非线性多目标规划模型，采用多层嵌套遗传算法求解方式实现对交叉口信号配时区间的优化,但该方法的控制效果也不理想。本文引入模糊控制理论，设计了一种新型的智慧城市路口交通灯配时优化方法，切实提高了智慧城市路口交通灯配时优化效果，缓解了交通路口的拥堵情况。

1 模糊控制方法

1.1 PID 控制器

PID 控制器的运行是根据输入信号的比例、积分以及微分关系，实现对目标对象按需控制的目的。PID 控制器模块可以使待控对象的被占用时长趋于合理，与单纯积分控制的应用思想基本类似。在实现同等比例控制各个目标对象的同时，可以使下级设备保持自由运行状态，对传输信号的控制作用相对较轻，当信号样本单次输入量较大时，PID 控制器的运行速度会明显下降。为了保证待控对象的运行能力，在选择信号样本时应控制目标信号的单次输出总量，PID 控制器结构模型如图1所示。

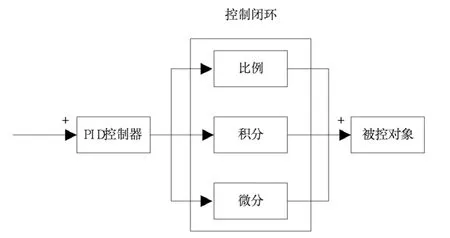
图1 PID 控制器连接结构

设α表示模糊性参数，c表示信号分配特征（辆），该特征通过信息增益提取，表示待分配信号在单位时间内的累积均值（辆/min），δ表示传输信号的实时系数(min），联系上述物理量，可将PID 控制器的运行表达式定义为：

式（1）中：W表示PID 控制器输出。如果α＞0 成立，表示信号传输方向与正负极标记方向相同；如果α＜0 成立，则表示信号传输方向与正负极标记方向相反。

1.2 整定参数

由于PID 控制器的运行会同时受到两种信号源的影响，在规范路口交通灯配时标准时，易出现信号传输行为混乱而造成控制效果不佳。为了避免上述情况的发生，可以根据PID 控制器元件的实时运行特点，求解整定参数并联合相关物理参量，完善模糊控制方法的应用流程[3]。整定参数，是对参数指标的整合与判定，前者意在将所有可能的物理参数聚合在一起，通过集中计算的方式选定最优解结果；后者则是在所有可能最优解中进行持续搜索，在去除局部干扰项参数后，得到唯一全局的最优解结果。在对路口交通灯配时优化过程中，只有保证整定参数求解结果的唯一性，才能实现对信号灯响应时长的准确分配，其整定参数的计算应满足如下表达：

式（2）中：Y表示整定参数的唯一解，β表示所选信号参量的控制系数，表示所选信号参量的模糊标记指征（辆），α、σ表示两个不相等的信号导入参数，I表示实时整定向量（辆/min），γ表示方向性参数，q1、q2、…、qn表示n个不同的数值解（min/辆）。为了充分发挥模糊控制方法的应用能力，在对方向性参数进行取值时应尽量避免取得零值或与零接近的物理参数。

2 智慧城市路口交通灯配时策略优化

在模糊控制方法基础上确定路口的实时交通状态，选择既定动作指令并联合奖励值函数，求解优化指数参量，实现对智慧城市路口交通灯配时策略的优化。

2.1 交通状态

智慧城市管理理念中，当交通路口拥塞程度达到一定数值水平后，当前路口便不具备再容纳其他车辆通行的能力。模糊控制理论认为，路口交通状态会受到时间、季节、温度等多项外界因素的影响，因此在制定交通灯配时策略时，可以适当调整信号灯的响应时长[4]。在优化交通灯配时策略时，交通状态只能作为一项参考变量。设表示拥塞参数，lmax表示交通灯配时参数的最大取值结果（s），lmin表示交通灯配时参数的最小取值结果（s），kmax表示单位时间内的最大车辆容纳数值（辆/min），kmin表示单位时间内的最小车辆容纳数值（辆/min）。在上述物理量的支持下，联合式（2），可将智慧城市路口的交通状态求解表达式定义为式（3）：

式（3）中：P表示智慧城市路口的交通状态。如果交通状态求解结果始终无法满足路口交通灯的配时要求，可能是拥塞系数的选值结果出了偏差，应在不更改车辆容纳数值与交通灯配时参数情况下对原拥塞系数进行调整。

2.2 交通灯显示状态选择

交通灯显示状态选择是指对交通灯的配时响应进行控制，即控制交通灯显示的状态，该状态分为红灯、绿灯和黄灯三种状态，分别对应车辆的停止动作、行进动作和转换动作（黄灯持续闪烁时，车辆在确认安全后可通行）。当车辆通行总和达到最大值时，交通灯的信号响应时长也达到最大值，在不考虑其他干扰情况下对交通灯显示状态进行选择，即配时响应的控制应注意以下问题：

（1）停止动作：在交通情况相对复杂的前提下，同一方向上需要通行的车辆相对较多，若红灯响应时间过长，容易导致严重的交通堵塞。为缓解城市路口的交通压力，停止动作在总配时中的占比时长一般相对较短。

（2）行进动作：在大多数城市路口的主要通行方向上，绿灯的响应时间都要大于红灯；而绿灯响应时间对应交通灯配时策略中的行进动作。为缓解城市路口的交通压力，行进动作在总配时中的占比时间必须大于停止动作。

（3）转换动作：连接停止动作与行进动作的交通灯表现形态被称为转换动作，也就是黄灯。在特殊路口处，黄灯如果持续闪烁，表示车辆在确认安全后可直接通过。因此，相较于停止动作与行进动作，转换动作在交通灯总配时中的占比时长并不完全固定。

2.3 奖励函数

奖励函数是分别计算车辆在智慧城市路网中各个路口的行进效率，根据模糊控制策略求解奖励函数表达式，对于效率的求解主要参考车辆通过路口所需的时间。在车流量保持均匀分布的情况下，只要控制车辆在各个路口的等待时长，就能避免车辆在城市路网中大量拥堵，从而实现对交通灯配时的优化处理。设表示车辆通行效率，表示实时车流量（辆/min），表示车辆在各个路口处的停留时间均值（s），ΔK表示车辆在单位时间内所通过的路口总量（辆），λ表示智慧城市路网中的路口分布系数。在上述物理量的支持下，联合式（3）推导基于模糊控制的奖励函数表达式（4）如下：

式（4）中：F表示奖励函数计算结果，用于评估车辆在智慧城市路网中行进效率。为了使交通灯配时优化结果更加贴合实际需求，要求ΔK指标的取值不宜过小，所以在运算需求上应尽量延长车辆在智慧城市路网中的单位行驶时长。

2.4 优化指数

为了规范交通灯配时标准，要按照奖励函数的计算结果，分别对红、绿信号灯的响应时长进行控制调节。规定b'表示绿灯信号调节参数，μ表示红灯信号调节参数，Μ表示交通灯转换向量，联合式（4），可将优化指数定义式表示为：

式（5）中：v表示优化指数，如果v计算结果等于“1”，表示在当前情况下的红灯、绿灯响应时间能够满足城市路口的通行需求，交通灯的响应时长也达到了最佳配时状态。

3 实例分析

基于模糊控制的路口交通灯配时优化方法，应以不确定交通需求下的配时优化模型作为实验组和对照组，设计如下对比实验分析。首先，模拟智慧城市路网晚高峰时期的路口交通情况，再分别按照实验组、对照组方法对该路口的交通灯配时进行调节，最后记录5 组不同的实验结果并将所得数值与交通灯理想配时情况进行对比，其城市路口路网信息数据如表1 所示。

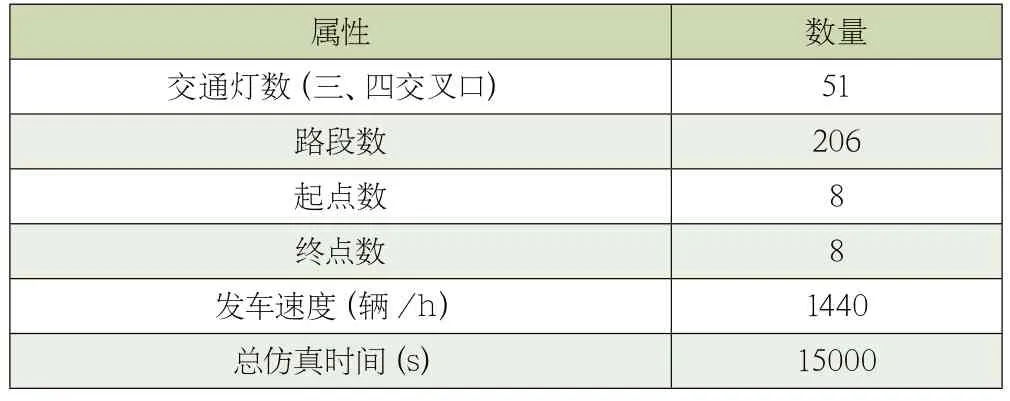
表1 路口路网信息数据表

表2 数据记录了实验组、对照组与理想情况下的交通灯配时情况。

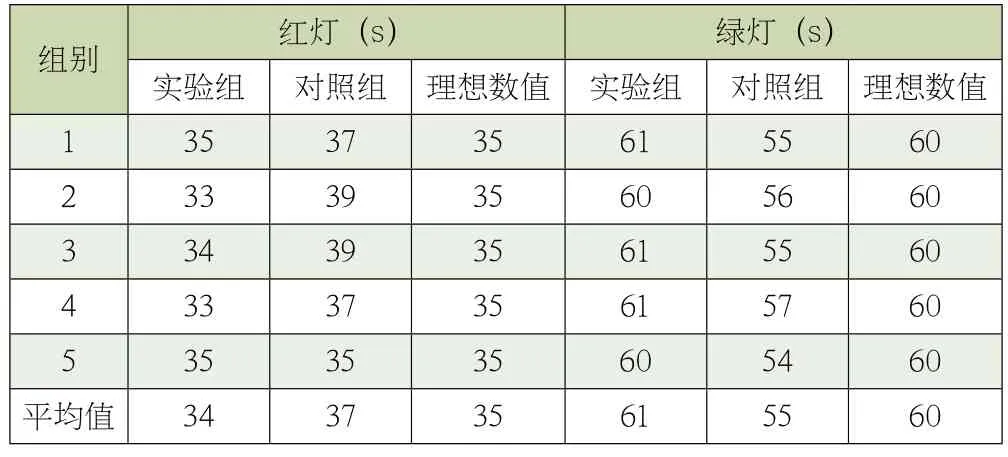
表2 交通灯配时数据表

分析表1 可知，与理想数值相比，实验组红灯配时均值缩短了1s，绿灯配时均值延长了1s。由于数值较小，其对于交通灯配时策略的影响程度可以忽略不计；而对照组红灯配时均值与理想数值相比延长了2s，绿灯配时均值缩短了5s，差值水平远高于实验组。综上可知，基于模糊控制的优化方法更符合规范交通灯配时标准和缓解优化智慧城市交通压力的实际需求，对当前城市路口的车辆密度推理得到表3 所示的车辆密度优化结果。

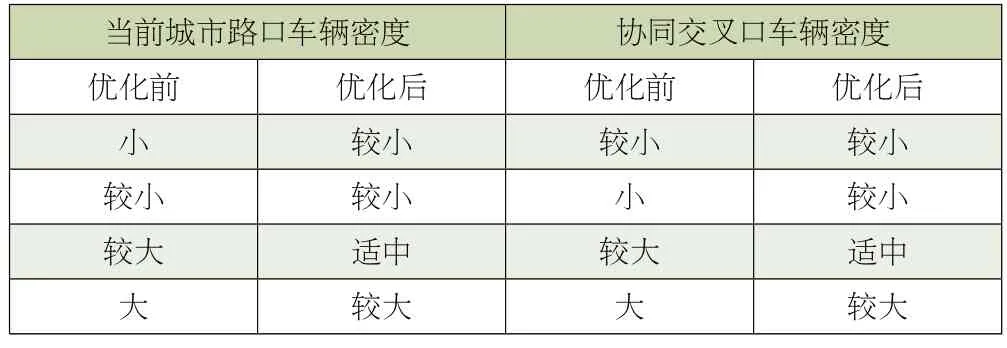
表3 车辆密度优化结果

表3 中的车辆密度由小到大排序为较小＞小＞适中＞较大＞大。根据表3 优化结果可知，应用本文方法后，当前城市路口车辆密度均得到了一定程度的降低。如果车辆密度为大时，无论是当前路口还是协同交叉口的车辆密度均降为较大，即车辆密度降低，避免了出现交通拥堵。

4 结语

通过实例结果分析，相比不确定交通需求下的配时优化模型，模糊控制交通灯配时优化方法联合了奖励值函数表达式，确定出优化指数的取值范围，实现了对拥堵路口的交通灯配时优化。随着这种新型优化方法的应用，城市路口的红灯、绿灯配时均值都不会与理想配时标准产生过大出入，表明其在有效缓解智慧城市路口交通压力上具有较高可行性和实用性。