公路地震灾害应急资源调度的多目标优化

马晨园，王 兵

(新疆大学，新疆维吾尔自治区 乌鲁木齐 830049)

0 引言

地震灾害会造成路段损毁，影响正常的交通运输。地震发生后，不同公路路段路基破坏程度不一，诱发路段损毁塌陷的时刻存在差异，即使同时受通讯阻断影响，各个公路损毁点信息上报时刻也存在差异；这些因素导致应急指挥中心获知各公路损毁点信息的时刻存在差异。而在应急资源受限条件下，从公路损毁点的附近应急点抽调大量应急资源前去处置会使应急点剩余资源难以满足后续公路损毁点的快速应急需求。

在交通安全工程领域涉及应急资源调度方面，学者们基于不同类型灾害的特性，设计了相应的数学模型进行优化调度：王付宇等[1]和邵泽军等[2]建立了关于时间和成本调度模型，并采用全局和局部混合模式的改进粒子群算法生成调度方案。张奕[3]和李志颖[4]构建了以应急加权总时间最短和应急救援运输成本最小的多目标应急救援资源调度模型，并设计了多目标粒子群算法对模型进行求解。李铭洋等[5]建立二阶段优化模型，以总撤离时间最短和总物资耗费最小为目标，解决了应急疏散及应急交通管理问题。赵学彧等[6]分析应急机构及灾害预防机构的分布特点，构造基于蚁群算法应急资源调度的路径规划模型。刁山虎[7]总结我国交通事故发生特点与处置难点，并提出具有针对性应急救援对策。钟卫平[8]建立了资源限制下的动态资源调度模型，实现多个需救点调度资源的最优化分配。王涛[9]考虑救援过程中各种影响时间的因素，建立了应急救援单边模糊时间窗模型。于福莹等[10]以应急响应时间最小为目标，同时满足事故点应急资源的最大需求，建立了分阶段协作救援资源调度模型。吴典文等[11]基于重心位置法调整乘客需求点的位置，根据聚类簇重心确定停靠站位置；以系统运营成本最小为目标构建了车辆路径和发出车型的协调调度模型，并运用模拟退火算法求解优化模型。综上所述，可知以上学者所建立的资源调度模型大多适用于交通事故应急救援，其原理不适用于地震灾害背景下损毁公路应急处置领域；上述研究以单个灾害、多个同时发生灾害的快速救援为目标，缺少以快速处置单个灾害且充分预防未来随机发生灾害为目标方法研究。本文通过分析损毁公路应急处置机理及应急资源优化配置理论，构建多目标应急资源指派模型，以生成合理资源调度方案。

1 问题描述与假设

针对单个公路损毁点，从多个应急点中选派一定数量的应急装备前去处置，在满足快速抢通当前受灾路段的基础上，各个应急点的剩余资源也能够对未来的损毁时间和地点均随机的损坏路段进行快速处置。基于此，给出假设条件：

a.调用的应急装备同时出发。

b.应急装备到达灾害点便开始作业。

c.后续公路损毁点的损毁地点随机，损毁量与距震源的距离成负相关。

d.后续公路损毁点信息传达至应急指挥中心的时刻随机分布在首个公路损毁点应急过程之中。

2 多目标应急资源指派模型

2.1 应急处置时长函数

接到调度命令后，各个应急点的应急装备同时出发，沿着各自的派遣路线陆续到达公路损毁点，总处置速度阶跃上升，当装备全部到齐后，总处置速度达到最大，并维持到灾害处置完毕，故从应急装备出发到灾害处置完毕对应的时间即为应急处置时长，见图1。

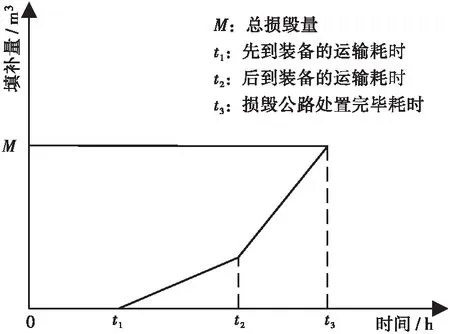
图1 应急处置流程

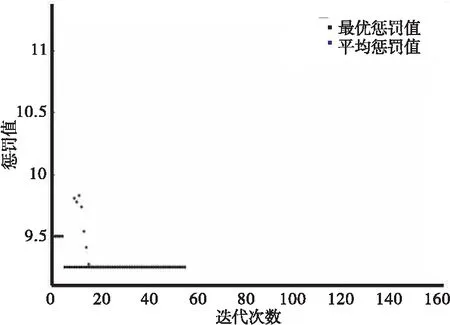
设定某一公路损毁点的损毁量为M，并派两个应急装备前去处置，处置速度分别为v1、v2，运送时长分别为t1、t2，且有t1

(1)

其中，式(1)中的v1(t2-t1)代表先到的应急装备已填补的填补量，可知M-v1(t2-t1)代表两个应急装备将要一齐处置的剩余填补量，[M-v1(t2-t1)]/(v1+v2)则表示为较晚到达损毁点的应急装备的处置时长。从式(1)可知，应急装备的运送时长越短，处置能力越高，则应急处置时长越短，进一步化简得：

(2)

不失一般性，设共有n个应急装备可供调用，应急装备的处置速度为vi，运输时长为ti，同时引入0-1决策变量xi，则应急处置时长可表示为：

(3)

考虑到公路地震灾害具有阻断交通的作用，故应急装备只能选择受灾路段的一侧作为目标派遣地，于是对式(2)做出扩展：

(4)

2.2 应急点应急能力削弱度函数

当仅以快速处置损毁公路为目标来抽调资源，会削弱应急资源配置的均衡性，易导致某个应急点的资源被过度占用，当该应急点附近公路发生损毁后，则需调用远处资源来处置，导致该灾害的处置时长大大增加。为降低抽调资源对应急资源配置均衡性的削弱程度，建立应急点应急能力削弱度函数，以提高整个应急体系的鲁棒性，见式(5)。

(5)

式中：pi为调用第i个应急装备惩罚系数。pi与该应急装备所在应急点应急范围[12]内(应急点与其应急范围内的灾害点的最短距离为最小)的潜在损毁量Mi和应急装备重要度oi相关，见式(6)。

pi=Mioi

(6)

其中，应急装备重要度oi即该应急装备的处置速度占其隶属应急点中所有应急装备处置速度总和的比重；潜在损毁量Mi主要与应急点应急范围的震中距相关。

2.3 总运输成本函数

为避免应急装备运输时长远大于其作业时长，以提高应急装备的利用率，故给出总运输成本函数，见式(7)。

(7)

2.4 确定约束条件

首先，一个应急装备无法同时派遣至两个作业区域，其次，灾害点作业区域有限，故派遣至受灾路段某侧的应急装备总数不得超出其限制k，于是可得如下约束条件：

(8)

3 模型转化

本文采用线性加权法对上述目标函数进行加权，见式(9)。

(9)

a.建立多目标层次结构。

只考虑应急处置时长、应急点应急能力削弱度、总运输成本3个因素，构建多目标层次结构，见图2。

图2 决策目标层次结构

b.应用1-9标度法，考虑快速应急需求和应急救援低经济性，确定指标间的相对重要性，如表1所示。

表1 各个指标的相对重要性

(10)

使用Excel软件对矩阵A进行规范化，得到矩阵B。

(11)

求取矩阵B各行元素之和，得到矩阵C。

(12)

使用Excel软件对矩阵C进行规范化，得到矩阵W。

(13)

最后对决策目标判断，检验其目标的一致性，并对一致性指标CI(在公式中用CI表示)进行求解。

(14)

(15)

通过权重评定表找到随机指标RI(在公式中用RI表示)，然后求一致性比例CR(在公式中用CR表示)，见表2。

表2 权重评定表

(16)

由于CR小于0.1，故所求结果在正常范围内，其中各个目标权重α1=0.67、α2=0.3、α3=0.03。

4 遗传算法求解

a.初始化操作：以应急装备总数作为染色体长度的参考指标；采用二进制编码，以满足变量类型要求；根据应急装备总数确立种群数量；交叉、变异概率及收敛精度取默认值即可。

b.初始化种群：随机生成第一代种群。

c.用适应度函数评价种群优劣度，判断是否满足终止条件，满足则输出最优解并停止；否则继续下一步操作。

d.对种群进行选择、交叉、变异，得到下一代种群，返回步骤c。

5 算例分析

5.1 单目标测试

新疆天山南麓附近发生地震后，造成点1处公路损毁，指挥中心调度各个应急点的资源去处置。灾害路段为双向二车道，即灾害点一侧只允许一个应急装备进行作业，拟从奎屯、石河子、乌鲁木齐、吐鲁番和库尔勒应急点调度资源前去处置，见图3、表3、表4。

表3 应急装备数据

表4 公路损毁点数据

图3 灾害点及应急点的分布

针对损毁点1，可调用资源有应急装备1、2、3、4、5，仅以应急处置时长最短为目标，利用MATLAB遗传算法工具箱计算应急处置时长T1(X1～X5代表“应急装备1-5是否派遣至灾害点A侧”，X6～X10代表“应急装备1-5是否派遣至灾害点B侧”)，并与盲目搜索方法(即先选择两个距灾害点最近的应急点，再从中选择处置速度最高的应急装备)作对比，见图4及表5。

表5 调度方案

(a)迭代图

5.2 多目标测试

针对损毁点1，可调用资源有应急装备1、2、3、4、5，以应急处置时长最短、应急点应急能力的削弱度最小和总运输成本最小为目标，计算应急处置时长T1并更新应急点库存数据，同时与盲目搜索方法作对比，见图5和表6。

表6 第一次调度方案

(a)迭代图

设定在损毁点1的应急过程中，上述路网中再次发生路段损毁，且损毁时间和位置均随机，损毁量与距震源距离呈负相关关系。为测试首次调度对应急点应急能力的削弱程度，即基于随机试验原则，使二次损毁发生地点均布于整个路网，采用盲目搜索方法分别对各个损毁点进行调度，计算平均应急处置时长Tz及总处置时长T3，见图6和表7。

表7 随机公路损毁点数据

图6 随机损毁点及应急点的分布

在经过一次资源调度后，处置后续随机损毁点所需应急装备库存数据发生变化，为更好体现第一次调度对第二次调度效果的影响，统一采用盲目搜索方法进行调度，计算可得如下结果，见表8和表9。

表8 第二次调度方案(基于应急资源调度模型抽调后的资源)

表9 第二次调度方案(基于盲目搜索方法抽调后的资源)

为方便对比，给出统计数据，见表10。

表10 统计数据

6 结论

针对单个公路损毁点的应急调度，与盲目搜索方法相比，多目标应急资源指派模型有如下几个特点：

a.多目标应急资源指派模型基于离散优化原理，可利用遗传算法搜索到全局最优解，故仅以应急处置时长最短为目标时，所生成方案的应急处置时长更短。

b.当以应急处置时长最短、应急点应急能力的削弱度和总运输成本最小为目标时，应急资源指派模型所生成方案的处置时长略微增加，但其所调用资源多来自于资源充沛、灾害风险低的应急点，故可保证每个应急点都剩有一定量资源来应对随机发生的灾害，降低了运输时长在整个应急处置耗时中的比重，提高了整体应急处置效率。