融合习题难度和作答经验的深度知识追踪模型

梁 祥, 刘梦赤*, 胡 婕, 冯嘉美

(1. 华南师范大学计算机学院, 广州 510631; 2. 湖北大学计算机与信息工程学院, 武汉 430062)

随着线上教育平台的发展,学生能够随时随地获取海量的在线学习资源,线上学习逐渐成为一种潮流。但线上学习存在一定局限性,首先是学生无法从线上教育平台得到实时的学习反馈,其次是老师无法从海量的信息中充分地分析、了解学生的学习情况。为了解决这些问题,智能导学系统(Intelligent Tutoring Systems,ITS)[1]在教育领域应势而生。ITS通过收集并分析学生的行为数据,为学生提供实时的学习反馈[2];老师也能通过ITS的分析结果了解学生的学习情况。知识追踪(Knowledge Tra-cing,KT)是ITS的核心技术之一,是一种对学生进行建模的方法,其任务就是通过学生的历史作答序列来评估学生当前的知识掌握状态,从而预测学生在未来练习中的表现。

贝叶斯知识追踪(Bayesian Knowledge Tracing,BKT)[3]是基于隐马尔可夫模型(Hidden Markov Model,HMM)来实现知识追踪的模型之一,该模型把学生对每个知识的掌握状态看作一个隐状态,之后根据学生的历史作答表现来更新隐状态的概率分布,即更新学生的知识掌握状态。2015年,PIECH等[4]将深度学习中的循环神经网络(Recurrent Neural Network,RNN)应用于知识追踪,提出了深度知识追踪模型(Deep Knowledge Tracing,DKT)。由于RNN采用高维并且连续的隐状态来表示学生的知识掌握状态,因此DKT模型的预测精确度高于BKT模型,而且DKT模型不需要对习题进行知识点标注,从而大大节省手工标注数据的人力成本。

尽管DKT模型解决了基于隐马尔可夫模型存在的问题,但忽视了对其他教育特征信息的利用,仅关注作答表现,无法对学生的学习过程进行全面建模。引入了更多特征信息的模型能更好地评估不同的特征信息对学生作答表现的影响,从而提高模型的整体预测能力和可解释性。因此,学者们在DKT模型的基础上,引入了习题或知识点之间的特征信息。如:WANG等[5]将习题与知识点之间的层次关系引入DKT模型,提出深层次知识追踪(Deep Hierarchical Knowledge Tracing,DHKT)模型;CHEN等[6]将知识点之间的先决条件关系引入DKT模型,提出先决条件驱动的深度知识追踪(Prerequisite Driven Deep Knowledge Tracing,PDKT)模型。另外,学者们从学生的角度出发,引入与学生有关的特征信息来提升模型的预测能力和可解释性。如:MINN等[7]使用机器学习的K-mean聚类算法,对学生在某一时间段的表现情况进行动态分类并应用于DKT模型中,提高模型对学生知识掌握状态的个性化评估能力;NAGATANI等[8]结合学生遗忘相关的特征信息来表示学生的遗忘行为,以此分析学生的遗忘行为对知识掌握状态的影响;李晓光等[9]提出了兼顾学习与遗忘行为的深度知识追踪模型(LFKT),取得了较好的预测效果。

上述模型虽然在一定程度上解决了深度知识追踪模型存在的一些问题并取得不错的改进效果,但大部分模型只是单独考虑习题或学生的特征信息,没有综合考虑习题和学生的特征信息。因此,本文提出了融合习题难度和作答经验的深度知识追踪模型(Deep Knowledge Tracing Model by Integrating Problem Difficulty and Answering Experience,DKT-DE)。通过引入习题难度和学生答题经验来丰富输入层的特征信息,使模型能够考察其对学生知识掌握状态的影响,从而更好地预测学生未来的作答表现,并且这些特征信息不需要人工进行标注。

1 DKT-DE模型

1.1 问题定义

知识追踪旨在通过学生的历史作答序列来评估学生当前的知识掌握状态,在此基础上预测其未来的作答表现。其形式化描述为:通过学生历史作答表现序列(x0,…,xt)来评估其当前的知识掌握状态st,从而预测学生在习题qt+1Q上的作答表现rt+1。其中:Q为习题集合;xi=(qi,ri)是一个二元组,表示学生在i时刻的作答表现;qiQ表示学生在i时刻作答的习题id;ri{0,1}为作答结果,0表示作答错误,1表示作答正确。

1.2 DKT模型

2015年,PIECH等[2]将RNN应用于知识追踪领域,提出了DKT模型。该模型的输入为学生的答题序列;在输入层中,采用One-Hot方式对学生在t时刻的答题情况xt=(qt,rt)进行编码;隐藏层的隐状态ht表示学生在t时刻的知识掌握状态,与学生在t时刻的作答表现xt和上一时刻的知识掌握状态ht-1有关;输出层yt是一个维度为习题集合大小的向量,由知识掌握状态ht决定,表示学生在t时刻对每个习题的答题正确率。

1.3 特征表示

已有研究[10]表明习题难度对学生学习过程有巨大的影响。对于大多数学生而言,当他们在最初几次作答难度较大的习题时,出错的概率会比较大。即使在多次对类似习题进行尝试后,出错的概率仍然很大。因此,通过引入习题难度来对学生的学习过程进行建模,能够帮助模型更准确地评估学生的知识掌握状态。为了减少专家标注带来的人工成本,本文实现了文献[10]提出的算法,并将其用于习题的难度评估。具体描述如下:

(1)

其中:D(qj)表示习题qjQ的难度等级,Q为习题集合;dja表示难度等级D(qj)的One-Hot编码,a为习题难度的分类数,Nj表示作答过习题qj的学生集合;rij表示学生i首次作答习题qj时的结果,若rij=0则认为作答错误。如果习题qj的作答人数不满足最低数量,即小于10人时,则将习题qj的难度等级D(qj)设为默认值a。

从学生的角度来看,学生之间也同样存在差异,因此,引入学生的个性化信息是极其重要且有必要的。随着练习次数的增多,学生能力也会随之发生变化,本文使用作答经验对学生能力进行个性化表示,其描述如下:

F(cj)1:z=Correct(cj)1:z-Incorrect(cj)1:z,

(2)

其中:Correct(cj)1:z和Incorrect(cj)1:z分别表示从时刻1到时刻z,学生在知识点cjC上的作答正确次数和作答错误次数;C为知识点集合;F(cj)1:z为作答正确次数与作答错误次数的差值;E(cj)1:z[-b,b](b+)为学生在知识点cj上的作答经验值,用ejz2b+1表示作答经验值E(cj)1:z的One-Hot编码。为评估不同经验值对学生作答正确率的影响,将式(2)应用于ASSISTments2009、ASSISTments2015、ASSISTments2017数据集,并设置参数b为8。实验结果(图1)显示:学生的作答经验值越高,其对应的平均作答正确率越高。

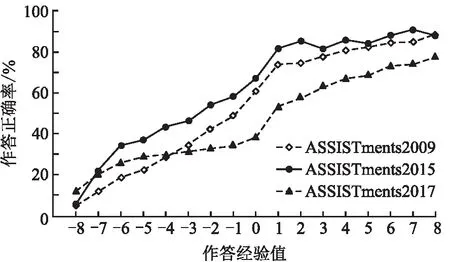
图1 作答经验值与正确率的关系图

1.4 模型结构

DKT模型的不足之处在于其假设习题难度和学生的学习能力是相同的。DKT-DE模型从习题和学生层面的角度出发,将习题难度和学生的作答经验相结合,融入DKT模型中,使其能够更好地评估学生的知识掌握状态,以提升其预测学生未来作答表现的精确度。

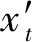
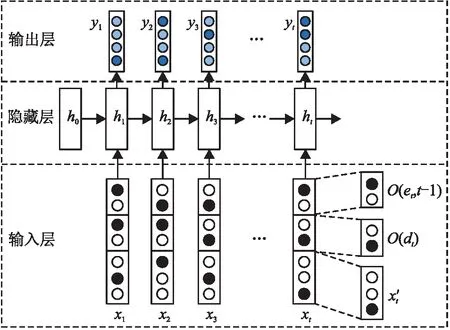
图2 DKT-DE模型的结构图

(3)

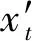
在隐藏层中,使用LSTM网络对学生的学习行为进行建模,隐藏层状态htk表示学生在t时刻的知识掌握状态,k为隐向量大小。ht与当前时刻的输入xt和上一时刻的知识掌握状态ht-1有关,计算公式如下:

ht=LSTM(xt,ht-1)。

(4)

在输出层中,ytm表示t时刻学生作答正确的概率,m为习题集Q的大小。yt的计算公式如下:

yt=σ(Wyhht+by),

(5)

其中,Wyhm×k为输出权重矩阵,bym为输出层的偏置项,σ(·)为Sigmoid激活函数。

本文通过最小化模型预测的作答结果yt与学生真实的作答结果rt之间的二分类交叉熵损失函数来优化各个参数。具体损失函数如下:

(6)

2 实验

在3个公共数据集上,对DKT-DE模型与5个基线模型进行比较实验;同时,进行了消融实验,以证明DKT-DE模型的稳定性及融合特征信息的有效性。

2.1 数据集

实验使用的数据集是ASSITments2009[11]、ASSITments2015[12]和ASSITments2017[13]。具体信息如下:

(1)ASSISTments2009:该数据集收集了ASSISTments在线教育平台2009—2010学年的学生交互信息,被广泛应用于知识追踪任务。本实验使用了该数据集中的skill-builder数据集,其中包含4 151名学生、110个知识点和325 637条作答记录。

(2)ASSISTments2015:该数据集也来自于ASSISTments在线教育平台,收集了2015—2016学年的学生交互信息。在预处理过程中,删除作答情况不为0或1的记录,处理后的数据集包含19 840名学生、100个知识点以及683 801条作答记录。该数据集由于学生人数多,因此其学生平均作答次数少于ASSISTments2009数据集的。

(3)ASSISTments2017:该数据集由ASSISTments在线教育平台提供,包含686名学生、102个知识点和942 816条作答记录。该数据集的特点是交互作答记录数较多、学生的平均作答次数较多。

2.2 模型训练

将数据集按照8∶2的比例随机划分为训练集和测试集;其中训练集中的80%数据用于模型训练,剩余20%作为验证集,进行5折交叉验证。使用Adam优化器[14]对模型进行训练,隐向量大小设为200;使用mini-batch加快训练速度,将batch-size设为32,学习率设为0.005;在训练过程中使用Dropout技术[15]防止模型出现过拟合的现象,比例设为0.4。由于输入层使用了Embedding技术对输入进行编码,因此将Embedding size设置为log2m,其中m为对应数据集的习题数量。习题难度的分类数a设置为10,作答经验b设置为8。

2.3 评价指标

本文采用了知识追踪模型的常用评价指标AUC(Area Under the ROC Curve)[16]来衡量模型的预测能力。AUC为接收者操作特征(ROC)曲线与坐标轴围成的面积,取值范围为0～1。如果模型的AUC值为0.5,说明模型没有实际意义,仅仅是随机猜测;AUC值越接近于1,说明模型的预测能力越强。

2.4 实验结果与分析

2.4.1 对比实验 为了验证DKT-DE模型的预测能力,在3个公共数据集上,将5个基线模型(BKT、DKT、DKVMN、DKT+、SAKT模型)与DKT-DE模型进行对比实验。为了减少实验误差,对每个模型重复5次训练,每次训练均进行随机初始化,最终取模型在测试集上的AUC平均值作为模型评估结果。

由实验结果(表1)可知:(1)基于深度学习的知识追踪模型整体优于基于隐马尔可夫模型的BKT模型。(2)DKT模型在3个数据集上的预测表现稍优于DKVMN模型[17],这在文献[18-19]中的实验部分也有所表现。(3)DKT+模型[20]在DKT模型的基础上引入正则化参数来改进其损失函数,使得DKT+模型的预测能力整体优于DKT模型,在ASSITments2009、ASSITments2015、ASSITments2017数据集上的AUC平均值分别提升了0.80%、1.79%和1.67%。(4)基于注意力机制的SAKT模型[18]的预测能力表现整体逊于DKT、DKVMN模型。(5)与DKT模型相比,DKT-DE模型在ASSITments2009、ASSITments2015、ASSITments2017数据集上的AUC平均值分别提升了3.60%、4.28%、3.19%;与基线模型中预测表现最好的DKT+模型相比,DKT-DE模型在ASSITments2009、ASSITments2015、ASSITments2017数据集上的AUC平均值分别提升了2.78%、2.44%、1.50%,因此可知DKT-DE模型在3个数据集上的表现均优于其他模型。

表1 各模型在测试集上的AUC平均值

2.4.2 消融实验 为了评估习题难度和学生作答经验对提高模型预测能力的贡献,在ASSITments2009、ASSITments2015、ASSITments2017数据集上,通过消融实验来进一步评估本文提出的DKT-DE模型的性能。将仅融合习题难度的DKT模型记为DKT-Diff模型,仅融合学生作答经验的DKT模型记为DKT-Exp模型。由实验结果(表2)可知:习题难度和学生作答经验对提高模型预测能力均有所贡献,融合2个特征信息的DKT-DE模型的预测能力整体优于仅融入单个特征信息的DKT-Diff模型和DKT-Exp模型。

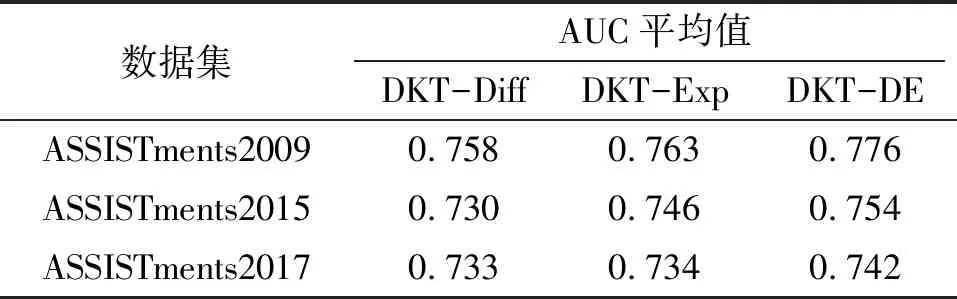
表2 消融实验结果

2.5 学生知识掌握状态追踪和评估

在Assistments2009数据集中随机抽取了一条学生的作答序列,使用DKT-DE模型对其知识掌握状态进行追踪和评估。图3为该学生的知识掌握状态热力图,图中给出学生在t时刻作答知识点qt的情况(rt)下,在t+1时刻作答其他知识点的正确概率。图块颜色的深浅表示模型预测学生未来作答正确概率的高低,作答正确概率越高则说明其知识点掌握状态越好。从图中可以看到:作答正确的次数越多,其对应知识点的掌握状态越好,符合学习的正向强化规律。

图3 知识掌握状态热力图

3 结束语

本文重点考虑了习题难度和作答经验对学生知识掌握状态的影响,并在DKT模型的基础上,提出了融合习题难度和作答经验的深度知识追踪模型(DKT-DE)。该模型将规范化的习题难度和作答经验作为模型输入层的特征信息,从而评估不同习题难度和作答经验对学生知识掌握状态的影响。实验结果表明:DKT-DE模型的预测能力优于其他基线模型,且引入的习题难度和学生作答经验特征对提升模型的预测能力均有所贡献。

因为在小规模数据上无法精确地评估习题难度和学生作答经验,所以DKT-DE模型在小规模数据上的表现并不理想。因此,后续研究可侧重于研究模型在小规模数据集上的优化,使其能够在不同的数据规模下发挥作用。