数据中心中机柜出风温度的快速模拟
张 博,廖炜铖,李学智,王 巍,李 震,3
(1.清华大学 航天航空学院,北京 100084; 2.中国移动通信集团黑龙江有限公司,黑龙江 哈尔滨 150028;3.河北清华发展研究院,河北 廊坊 065000)
0 引 言
随着信息技术的发展,数据中心的数量和规模逐年增大。数据中心的运行特性决定了其能耗较大,而空调系统的能耗在数据中心总能耗中仅次于信息设备[1]。合理的气流组织对降低数据中心的能耗,提供适宜的热环境至关重要。实验测试和数值模拟是研究数据中心气流组织的主要方法。工程实测成本较高,且在实验过程中,热环境可能偏离信息设备的承受范围,导致信息设备宕机。使用计算流体力学(CFD)软件模拟数据中心的气流组织以其成本低、风险低的优势逐渐受到关注。CHO等采用CFD模拟和实验测量发现地板下送风顶部回风的方式优于中侧送风顶部回风、同侧送回风、顶送侧回和下送侧回[2]。PATANKAR使用CFD模拟研究了数据中心中的气流分布,发现架空地板的高度、空调的位置、多孔砖的布置、多孔砖的开孔面积和挡板对流场影响很大[3]。CHO等通过CFD模拟发现空气回流发生在服务器上方2.1~2.7 m的位置,增加通道隔墙可以有效阻止空气回流[4]。LEE等使用CFD研究了冷通道封闭的数据中心,发现在机架顶部安装一个换热器和风机可以改善热环境[5]。XIONG等使用CFD对比了地板下送风、顶部送风和风扇墙系统对数据中心热环境的影响,发现使用风扇墙系统可以降低内部的热点温度[6]。MOAZAMIGOODARZI等使用CFD研究了冷却结构对数据中心能耗的影响,发现行间级冷却和机柜级冷却比房间级冷却更节能[7]。YUAN等使用CFD研究了柔性挡板和服务器倾斜角度对数据中心热环境的影响,发现服务器最佳的倾斜角度是30°[8-9]。TANG等使用CFD研究了数据中心的热环境,发现添加盲板和关闭非必要的多孔板可以使温度分布更均匀[10]。LU等使用CFD研究了不同结构的数据中心,发现提高架空地板的高度和降低开孔百分比可以改善数据中心的热环境[11]。NADA等使用CFD研究了空调的位置、开孔率和封闭冷通道对数据中心的影响,发现空调和冷通道之间的距离对空气回流的影响不大,封闭冷通道对高密度数据中心很有必要[12]。PHAN等研究了不同湍流模型和多孔砖模型对数据中心模拟精度的影响,发现修正体积力模型更适合描述多孔砖,零方程模型的计算精度与标准k-ε模型相当,且计算耗时少[13]。
使用CFD模拟可以获得数据中心的气流组织和热环境,但存在计算时间长、计算资源消耗大等问题。为了加快计算速度,HAN等通过简化近壁面处的湍流黏度,提出了快速流体力学仿真模型,但是该模型需要使用GPU才能实现加速的目的[14]。SAMADIANI等基于本征正交分解(POD)建立了数据中心的降阶模型,在重要尺度上求解降阶后的能量方程,计算速度是CFD模拟的250倍[15]。ATHAVALE等使用机器学习方法预测了机柜的进风温度,发现高斯过程回归(GPR)的预测精度高于人工神经网络(ANN)和支持向量回归(SVR)[16]。SONG等基于POD和非线性主成分分析建立了预测数据中心温度演化的简化模型[17]。PHAN等将CFD和POD结合,研究了入口质量流率、服务器热负载、机柜进风温度对热环境的影响,基于POD的降阶模型计算速度是CFD的600倍[18]。SEMPEY等在流场不变和忽略热源项的假设下,推导了能量方程的降阶模型,可以用来实时预测温度场[19]。FANG等对比了不同神经网络预测机柜出风温度的精度,发现径向基神经网络的预测精度较高[20]。CHOI等对比了自适应ANN和非自适应ANN预测机柜进风温度的精度,发现自适应ANN的预测精度更高[21]。WANG等对比了简化的传热模型和数据驱动的模型预测数据中心温度的精度,发现数据驱动的模型的精度高于传热模型,但是可解释性不如传热模型[22]。PARK等比较了滑动窗口、矢量自适应和矢量增强3种再训练技术对ANN预测精度的影响,发现滑动窗口方法的预测精度较高[23]。ASGARI等结合多区域模型和ANN建立了预测数据中心温度分布的灰盒模型,比黑盒模型具有更好的外推性能[24]。LIN等对比了SVR、GPR、XGBoost、LightGBM、ANN、LSTM等6种机器学习模型预测数据中心温度的精度,发现集成学习方法的预测精度较高[25]。LIU等在多区域模型的基础上,建立了预测数据中心温度的状态空间模型,与CFD模拟结果相比,误差小于10%[26]。GUPTA等基于多区域模型和流动网络模型优化了数据中心的功率分配[27]。HABIBI等基于势流模型构造了数据中心的降阶模型,但由于节点数目较多,瞬态模拟时间较短[28]。
本文以某数据中心为研究对象,建立了CFD模型,使用6 SigmaRoom软件计算了机柜的出风温度,并基于POD建立了机柜出风温度的降阶模型,对比了回归树、提升树、SVR、ANN、GPR、三次样条插值、分段三次Hermite插值对机柜出风温度的预测精度。
1 模型和方法
1.1 计算模型
图1是数据中心的平面图,长33.6 m,宽13.2 m,高4.5 m,包括7台空调和6个微模块。每个微模块包含22个机柜和末端的控制柜,机柜尺寸为0.6 m×1.2 m×2.2 m。机柜的发热功率为3 kW,控制柜不发热。架空地板高0.8 m,多孔地板的开孔面积为50%,冷通道和热通道的尺寸均为1.2 m×2.2 m×7.8 m,并封闭冷通道。送风口面积为1.26 m2,回风口面积为1.8 m2。

图 1 数据中心的平面图
精密空调产生的冷空气通过架空地板送至机柜附近,被机柜内的风扇吸入机柜内部对设备进行冷却。由于数据中心中空气的流速不会超过0.2倍的音速,可以忽略空气的可压缩性。采用不可压缩流体假设,数据中心中空气流动换热的通用控制方程可写为

(1)
式中:ρ为密度;U为速度;φ为通用变量;Γφ为广义扩散系数;Sφ为广义源项。其具体含义见表1。表中:μ为黏度;p为压力;x为位置;β为热膨胀系数;T为温度;g为重力加速度;κ为热导率;cp为比热容;ST为热源项。

表 1 通用控制方程中相应变量的含义
式(1)描述的流动可以是层流、湍流或层流和湍流之间的过渡流。湍流是一种高度复杂的三维非稳态、带旋转的不规则流动,在实际工程中,求解的是Reynolds时均方程(RANS),可写为

(2)

Gk+Gb-ρε
(3)
(4)
式中:σk、σε是湍流普朗特数;Gk、Gb与湍动能有关;C1ε、C2ε、C3ε是k-ε模型中的常数。在固体壁面附近的黏性底层,流动与换热的计算采用标准壁面函数法完成。
1.2 本征正交分解
(5)
式中:φ为一组正交基函数;ai为基函数的系数;N为基函数的个数,且使正交投影的误差最小,即
(6)
(7)

(8)
式中:δ为任意较小实数;Ψ为除φ外其他任一空间基函数。SIROVICH引入了快照法,经过数学推导,得到POD模态的控制方程[29],即
Rφ=λφ
(9)

(10)
POD基函数对应的谱系数通过投影得到:
(11)
为了在样本包含的设计参数区间内,使用降阶模型得到样本外其他设计参数下的物理场,需要求出这些设计参数下对应的谱系数,且要求POD基函数没有较大改变。本文分别使用了回归树、提升树、SVR、ANN、GPR、三次样条插值和分段三次Hermite插值预测谱系数。
决策树是将空间用超平面进行划分,每次分割时,将当前的空间一分为二。一个回归树对应着输入空间的一个划分以及在划分单元上的输出值。假设将输入空间划分为K个单元R1,R2,…,RK,且在每个单元Ri上有一个固定的输出值ci,则回归树模型可表示为
(12)
最优输出为
(13)
提升树以回归树为基本学习器,其可以表示为回归树的加法模型,即
(14)
支持向量机(SVM)是在n维空间中找到一个对数据点进行明确分类的超平面。SVR的原理与SVM相同,是在n维空间中找到一个数据点数最多的超平面。给定训练样本D={(x1,y1),(x2,y2),…,(xm,ym)},学得形如
(15)
的回归模型,使得fSVR(x)与y尽可能接近,其中κ(x,xi)是核函数,表2列出了常用的核函数。

表 2 常用核函数
ANN(artificial neural network)是一种模仿人脑神经网络的数学模型,用于对函数进行近似。ANN包括输入层、隐藏层和输出层,激活函数为Sigmoid函数。一个神经元的输入和输出可以用式(16)表示,即
(16)
本文分别使用了2层神经网络和3层神经网络进行预测,每层神经网络包含10个神经元。 GPR是使用高斯过程先验对数据进行回归分析的非参数模型。高斯过程是一组随机变量的集合,且该集合中任意有限个变量均服从联合高斯分布。一个高斯过程f(x)的概率特性由它的均值m(x)和协方差函数K(x,x′)唯一决定,其中
m(x)=Ε[f(x)]
(17)
K(x,x′)=Ε{[f(x)-m(x)][f(x′)-m(x′)]}
(18)
式中:x和x′是自由变量。GPR中常用的协方差函数包括指数函数、平方指数函数、二次有理函数、马顿函数。三次样条曲线是通过样本点的光滑曲线,可以通过求解三弯矩方程组得出曲线函数组。三次样条插值就是用三次样条曲线来进行插值。分段三次Hermite插值是在2个样本点间使用Hermite三次多项式连接。相比于三次样条曲线,分段三次Hermite插值不要求二阶导数相等。
2 结果与分析
2.1 网格独立性验证
在小型数据中心中,机柜的功率不高,因此在网格独立性验证中,设定机柜功率为3 kW,7台空调的风扇转速均为80%,送风温度为25 ℃,分别划分了3 118 648、3 535 792、3 778 362、4 283 748和5 637 556等5套网格,进行网格独立性验证。图2(a)、(b)分别展示了5套网格下计算的空调回风温度和机柜出风温度,3 118 648网格下的计算结果与5 637 556网格下的计算结果相差小于0.3 ℃,表明3 118 648网格已经克服网格依赖性,用于后续的CFD模拟。

(a) 5套网格下计算的空调回风温度
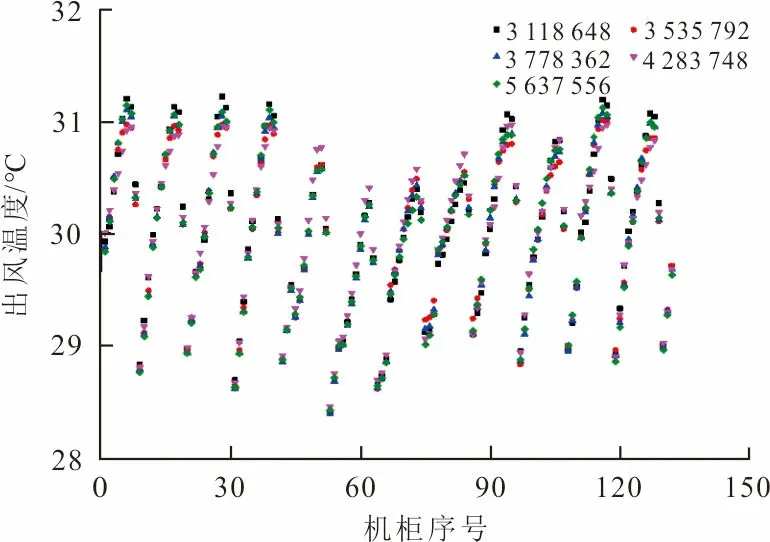
(b) 5套网格下计算的机柜出风温度
2.2 空调停机下的机柜出风温度
数据中心在运行过程中会出现空调停机检修的情况,因此使用CFD软件,模拟了单个空调停机时的工况,机柜功率为3 kW不变,其余空调全开,并计算每个微模块的出风温度,结果如图3所示。从图3可知,微模块每个机柜的出风温度并不相等,远离空调送风口的机柜出风温度更低,靠近空调送风口的机柜出风温度较高。由热平衡关系可知,靠近送风口的机柜吸入的冷气流少于远离送风口的机柜。这是因为根据伯努利定律,当总压一定时,风速越大,静压越小。在送风口附近,风速较大,使空气被快速吹到了后端,反而不易把气流吹入微模块中。由图3(a)、(b)可知,空调1对微模块1的影响最大,其次是空调2,空调3、4、5、6、7对微模块1的影响相似。空调对微模块的影响显著依赖于空调与微模块的距离。由图3(c)、(d)可知,对微模块2影响最大的是空调2和3。由图3(e)~(l)可知,微模块3、4、5、6中远离送风口的机柜出风温度在空调4、5、6、7停机时较高,靠近送风口的机柜出风温度在空调3、4、5、6停机时送风温度较高,说明这些微模块中远离送风口的机柜受空调4、5、6、7的影响更大,靠近送风口的机柜受空调3、4、5、6的影响更大。由图3可知,距离微模块最近的2个空调对微模块的影响最大,其余空调对微模块的影响不大。

(a) 微模块1左出风面

(b) 微模块1右出风面

(c) 微模块2左出风面

(d) 微模块2右出风面

(e) 微模块3左出风面

(f) 微模块3右出风面

(g) 微模块4左出风面

(h) 微模块4右出风面
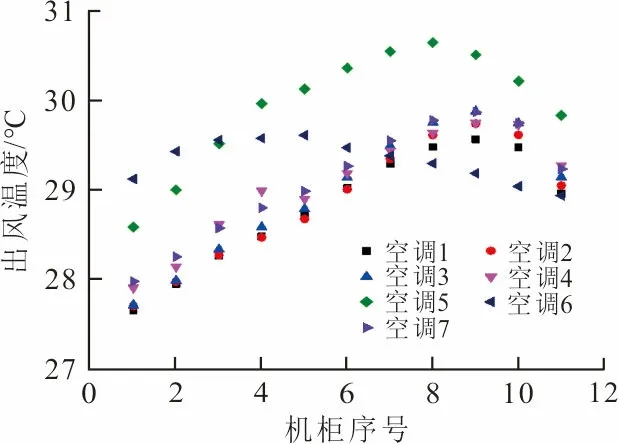
(i) 微模块5左出风面
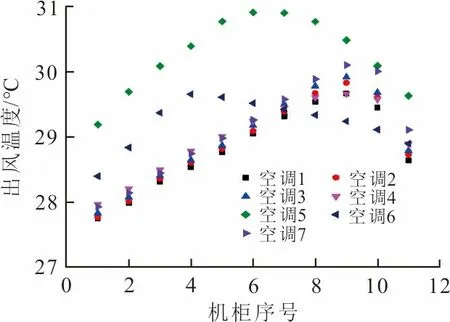
(j) 微模块5右出风面

(k) 微模块6左出风面
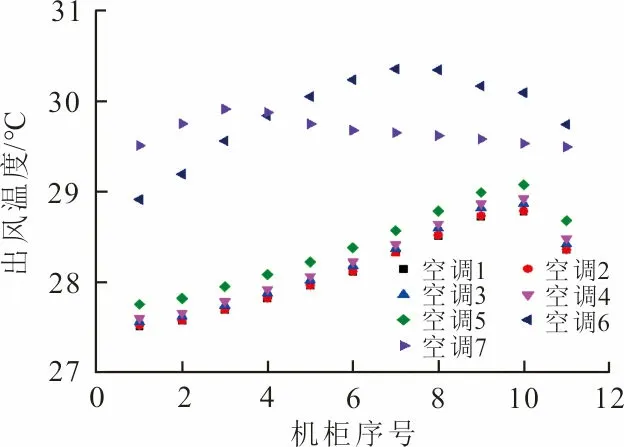
(l) 微模块6右出风面
2.3 降阶模型的结果
CFD模拟可以获得数据中心热环境,但是计算量大,下面使用POD对CFD模拟获得的温度场数据进行降维,抽取主要特征。降维得到的空间基函数也称为POD模态,在相似工况下几乎不变。每个POD模态对应的广义能量体现了该POD模态包含信息的多少。图4展示了微模块出风面温度场对应的POD模态的能量占比,M代表微模块(1~6是微模块序号),L代表左出风面,R代表右出风面。其中低阶模态的能量占比大,高阶模态的能量占比小,因此低阶模态比高阶模态包含更多的温度场信息,只需选取前几阶模态就可以重构温度场。
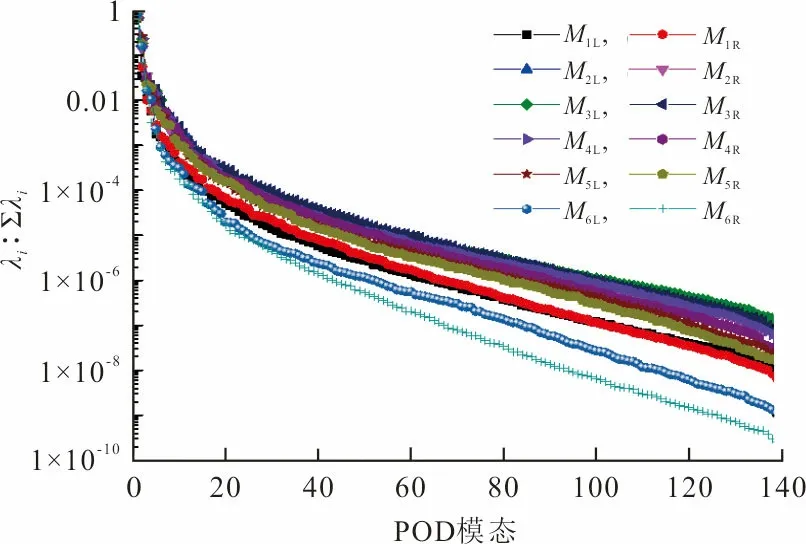
图 4 POD模态的能量占比Fig.4 Energy proportion of the POD mode
GHOSH等对POD建模进行了误差分析,认为POD建模的误差依赖于忽略的高阶模态[30]。这里选取前18阶模态重构温度场,以平衡计算效率和精度。
图5展示了空调1停机时,CFD计算出的微模块1的左出风面的温度场,使用18阶POD模态重构的微模块1的左出风面的温度场和二者的误差,其中最大误差为0.12 ℃。图中横纵坐标Z和Y分别代表微模块1左出风面的长度和宽度。其余微模块的出风温度场重构效果与之相同,因此使用18阶POD模态可以有效重构温度场。
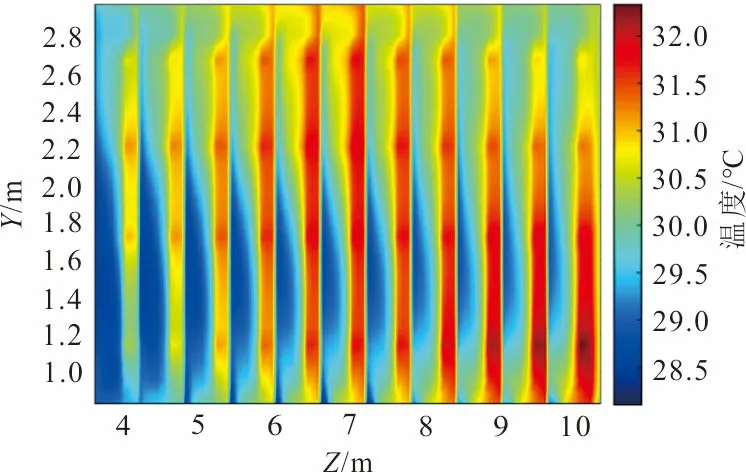
(a) CFD计算出的微模块1左出风面 的温度场

(b) POD重构的微模块1左出风面的温度场

(c) POD重构的温度场误差
为了在样本确定的区间内预测样本外的其他工况下的热环境,需要预测未知工况下POD模态对应的谱系数。图6(a)对比了几种机器学习模型在训练集上的确定系数R2和均方根误差ERMS,其分别定义为
(19)
(20)

为了测试机器学习模型的泛化性能,使用CFD软件计算了空调1和2送风量为76%、78%、82%、84%、86%时数据中心的温度场,抽取微模块1的左出风面作为测试集。图6对比了几种机器学习模型的泛化性能,其中FTM是精细树模型,SVR2是核函数为二次函数的SVR,SVR3是核函数为三次函数的SVR,SVRG是核函数为高斯函数的SVR,GPRQ是协方差函数为二次有理函数的GPR,GPRSE是协方差函数为平方指数的GPR,GPRM是协方差函数为马顿函数的GPR,GPRE是协方差函数为指数函数的GPR,BTM是提升树模型,NN2是两层神经网络模型,NN3是三层神经网络模型,可见协方差函数为二次有理函数的GPR具有最优的泛化性能。这是因为GPR使用高斯过程先验对数据进行回归分析,更适合低维和小样本的情况。

(a) 训练集上的确定系数和均方根误差

(b) 测试集上的确定系数和均方根误差
机器学习模型相当于建立一个与已知数据点距离最短的函数,而插值法则可以建立一个通过数据点的函数。因此在数据点准确已知时,插值法建立的函数逼近误差更小。下面使用三次样条插值和分段三次Hermite插值预测未知工况下POD模态的谱系数,并重构温度场。图7展示了三次样条插值和分段三次Hermtie插值预测的微模块1的左出风面温度场和CFD计算的温度场的最大温度误差,其中k是测试样本的序号。

图 7 三次样条插值和分段三次Hermite 插值的温度误差
可见2种插值方法的精度相似,最大误差为0.33 ℃。使用POD与机器学习方法或插值方法相结合预测温度场的计算时间不足60 s,使用CFD软件预测温度场的计算时间为2 h,计算速度提升了100多倍。
3 结 论
1) 本文首先使用CFD软件计算了多种工况下数据中心的热环境,对比了一台空调停机时微模块的出风温度,发现对微模块温度场影响最大的是距离微模块最近的空调。同一个微模块中的机柜的风量存在差异,远离空调的机柜的风量高于靠近空调的机柜。这是因为靠近空调处的压力较小,远离空调处的压力较大。
2) 以CFD软件计算的微模块出风温度为原始数据,使用POD进行降维,截取18阶POD模态重构温度场,最大误差小于0.2 ℃,说明POD方法的低阶模态包含了物理场的大部分信息,仅需截取少量低阶模态便可有效重构物理场。
3) 对比了回归树、提升树、支持向量回归、神经网络、高斯过程回归、三次样条插值、分段三次Hermite插值与POD结合预测相似工况下微模块出风温度的精度,发现高斯过程回归、三次样条插值、分段三次Hermite插值的预测精度高于回归树、提升树、支持向量回归和神经网络,计算速度比CFD软件快了100多倍,说明高斯过程回归、三次样条插值和分段三次Hermite插值更适合对小样本的数据进行建模。
4) 当使用高斯过程回归预测时,以指数函数为核函数时的预测精度高于以平方指数函数、二次有理函数或马顿函数为核函数时的预测精度。

